No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
(1) The simplex in a space Sn of order n (or n − 1 dimensions) is a set of n points a1 a2 …an which do not all lie in a subspace of Sn.
The elements of the simplex a1 a2 …an are the n points a1 a2 …an whieh are elements of order one, the 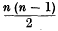 lines ar as which are elements or faces of order two, etc., etc., and finally the n primesa1 a2 … ar−1 ar+1 … an which are elements or faces of order n – 1.
lines ar as which are elements or faces of order two, etc., etc., and finally the n primesa1 a2 … ar−1 ar+1 … an which are elements or faces of order n – 1.
* The word ‘prime’ (due to Prof. H. F. Baker) is a convenient one for denoting a flat space of order n−1 situated in a flat space of order n. Flat spaces of order < n−1 may be called generally regions or spaces.
* The corresponding algebraic proposition may be found in Cullis, Matrices and Determinoids, Camb. Univ. Press, vol. 1.
* Proc. Camb. Phil. Soc., vol. 14, p. 475 (1908).Google Scholar
* Baker, , Principles of Geometry, vol. 3, pp. 144, 145.Google Scholar
† If by ‘line’ we mean a line of the complex L, and if we agree to consider for a moment all lines not belonging to L as non-existent, we can throw the theorem of the double-pentad in the following form, which is a fairly accurate caricature of the theory of the double-six:
Three lines have in general two common transversals; four lines have in general none. Consider four lines a1 a2 a3 a4 which have a transversal b5; every three of the lines have then a second transversal. Calling these second transversals b1 b2 b3 b4, the theorem of the double-pentad states that the four lines b1 b2 b3, b4 have themselves a common transversal a5 (provided al a2 a3 a4 cut out an equi-anharmonic range on b5). The two sets of five lines thus obtained are then symmetrically related, the lines ar bs meeting each, other if r≠s, and each set being such, that any four of its five lines have a common transversal which belongs to the other set.
* Two lines like a5, b5, which are the transversals of covariant self-apolar tetrads of tangents of a cubic curve, have some interesting properties. They are conjugate to each other in regard to any quadric circumscribed or inscribed to the cubic curve. From the binary point of view, these lines determine on the cubic curve two null pencils of triads (meaning by a null pencil, one which has any two of its members apolar), which may be called associated null pencils. The characteristic property of two associated null pencils Γ1 Γ2 is that, if abc, ab'c′ be members of Γ1, Γ2 respectively, the pairs bc, b′c′ separate each other harmonically. The converse theorem, that two pencils of cubics with this property are necessarily associated null pencils, is true with certain trivial exceptions. An interesting application of the idea of associated null pencils to the rational space-quartic curve C 4 may be mentioned. The curve C 4 possesses an infinity of tri-secants which lie on the unique quadric con taining it. The pencil of coUinear triads on C 4 is a null pencil, if its super-osculation points are coplanar. In this case we can accordingly seek for the associated null pencil, using the characteristic property stated. We easily find that the associated null pencil must consist of triads of points on the curve, the tangents at which are concurrent; we can show that the locus of the meets of the concurrent tangents is a conic through the super-osculation points. The existence of triads of concurrent tangents of a rational quartic with co-planar super-osculation points has been known for a long time (see Roberts, R. A., “The Unicursal Twisted Quartic,” Proc. London Math. Soc., vol. 14, 1st series).Google Scholar
* It amounts, as already remarked, to 2m− 1 conditions for m = 6, to 2m conditions for m = 5, and to 2m − 2 conditions for m = 4. It is perhaps not unlikely that it would amount to fully 2m conditions for higher values of m.