1. Introduction

Recent progress in the construction of nitride based optoelectronic devices has been achieved by application of heteropitaxial growth techniques Reference Akasaki and Amano[1] Reference Mohammad, Salvador and Morkoç[2]. Nitride layers were grown sapphire Reference Nakamura, Mukai and Senoh[3] as substrate and despite large lattice mismatch with GaN both LED and lasers were constructed Reference Nakamura, Senoh, Nagahama, Iwasa, Yamada, Matsushita, Kiyoku and Sugimoto[4]. At the present a nitride based laser is able to work only for a limited time. In order to extend the work period of the laser, the quantum well structures should be improved.

Heteroepitaxial technologies will always suffer from the differences in the properties of substrate and the layers. Therefore development of homoepitaxial growth techniques is the best way to achieve fast progress in the laser technology. That requires single GaN crystals of substrate quality and the sizes of order of 1 cm. Growth of GaN single crystals is difficult because it requires high activity of nitrogen and high temperatures Reference Edgar[5].

Gallium nitride single crystals can be grown by ammonia Reference Elwell and Elwell[6] or by high pressure nitrogen methods Reference Porowski, Grzegory, Jun, Jurczak and Baranowski[7] Reference Grzegory and Krukowski[8]. Since NH₃ is unstable in the temperatures above 1100°C, the ammonia method suffers from low solubility of nitrogen in the liquid gallium. On the contrary the high N₂pressure method allows to extend the temperature range of the growth to 1500°C for nitrogen pressures close to 20 kbar. So high pressure changes equilibrium and transport properties of nitrogen drastically. On the contrary, the physical properties of liquid gallium remain essentially unchanged. For high pressure the volume of the chambers is limited which leads to very steep temperature gradients close to the growth zone. Therefore the control of the temperature in the high pressure chamber is of a primary importance to the design of high pressure growth apparatus.

In this paper we will give an outline of the thermodynamic properties of nitrogen in pressures up to 20 kbar and the temperatures up to 1600°C. Then we employ, finite element code FIDAP [9] to obtain the temperature inside high pressure chamber. The calculations of one-zone furnace are shown. These results are analysed and compared with the data obtained in high pressure experiments.

2. Nitrogen properties under high pressure

High pressure of the nitrogen drastically changes its physical properties. The most important effect is the increase of the density of the gas. This change of the nitrogen properties is largest in low temperatures. In particular strong repulsion of the atomic cores leads to the steep increase of nitrogen activity. It also enhances the direct transfer of the energy leading to the increase of thermal conductivity and shear viscosity.

2.1 Density and thermal expansion coefficient

The p-T-r equation of state of nitrogen was critically assessed by Jacobsen et al for the interval region extending from the triple point to the pressure up to 10 kbar and temperatures up to 2000K Reference Jacobsen, Stewart and Jahangiri[10]. The errors were smaller than 0.3% for the entire interval outside the critical region. The calculated density and thermal expansion coefficient obtained from extension of Jacobsen equation of state for higher pressures and temperatures are presented in Figure 1.

Figure 1a. High pressure isobars of nitrogen - density.

Figure 1b. High pressure isobars of nitrogen - thermal expansion coefficient.

2.2 Activity

The excess of free energy DG can be translated into the activity of the nitrogen a as follows:

(1)

Due to the repulsion of nitrogen atomic cores, free energy of nitrogen at higher pressure increases, especially in low temperatures. This increase is used in high pressure experiments to extend the stability range of GaN and plays crucial role in high pressure growth of gallium nitride. The nitrogen activity is presented in Figure 2.

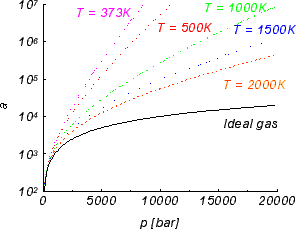
Figure 2. Nitrogen activity for several temperatures.

Figure 3. Heat capacity of nitrogen in high pressures.

2.4 Thermal conductivity

High pressure experimental investigations of nitrogen thermal conductivity were limited to pressures not higher than 1 kbar and the temperatures up to 1200K Reference Streett, Spain and Paauwe[11] Reference Le Neindre[12]. For higher temperatures nitrogen thermal conductivity was measured only for low pressures. The most successful extrapolation of thermal conductivity uses division into low density viscosity that accounts for the kinetic part of the energy transfer and the density dependent term which represents the transfer via potential energy Reference McLaughlin and Tye[13]. The physical conditions of our interests covers the same interval of the nitrogen densities, as those known from low temperature measurements Reference Streett, Spain and Paauwe[11] Reference Le Neindre[12] with the extension to higher temperatures. Therefore we expect that the expansion

(2)

is valid for the range of the densities of our interest. The density expansion represents the excess thermal conductivity with the precision better than 3% in the densities up to 1kg/m³. The zero density contribution l_o(T) can be represented by the series:

(3)

This expansion used scaling hypothesis of the temperature dependence of the collision integral crossection for the nitrogen at high temperatures. This contribution is remarkably well represented with formula (3), it recovers the experimental data with the precision better than 2% for the temperature range up to 2400 K Reference Stephen, Krauss and Laesecke[14]. Using these approach we obtained results for higher pressures which are presented in Figure 4.

Figure 4. Thermal conductivity of nitrogen under high pressure

The transition from potential to collisional energy transfer leads to the minimum known as Enskog minimum. The minimum shifts towards higher temperatures for higher pressures. For higher pressures the potential term dominates therefore the transition moves into higher kinetic energy values (i.e. higher temperatures).

2.5 Viscosity

The temperature dependence of the shear viscosity is presented in Figure 5. The zero density viscosity and thermal conductivity are related by heat capacity dependent factor:

(4)

Figure 5. Viscosity of nitrogen under high pressure.

where M - is the molecular mass and C_v - heat capacity under constant volume, which weakly depends on the temperature. The excess viscosity can be expressed in power of the density. The resulting temperature dependence shows again the Enskog minimum, which is shifted towards higher temperatures for higher pressures.

3. Finite element calculations

In the calculation we have used finite element code FIDAP [9]. The code is solving entire set of Navier-Stokes equations for liquid part of the system and the thermal conductivity equation for the solid part. In the nitrogen part the radiative heat exchange was also accounted for. The surfaces were assumed to be perfectly black bodies which is good approximation for the temperatures higher than 1200°C. The gallium liquid properties were assumed to be pressure independent. Similar assumption has been used for the heat conductivity in the solid part of the system.

The high pressure apparatus in the vertical configuration has been calculated. It consists of three tube steel chamber of the internal diameter of 40 mm and the length of 203 mm. The water cooling is used to keep the temperature of the chamber close to the equilibrium temperature. The temperature of the chamber is monitored during the entire growth process. The variation of the temperature do not exceed 10°C.

The heater is in form of graphite spiral. In these calculations the heater is represented by a uniform heat source of the total power equal to 1500W which is equal to the electrical power used in the growth experiment. The temperature distribution has cylindrical symmetry, therefore in Figure 6 we present the cut though the simplified design of the chamber and the isotherm of obtained in the calculation.

Figure 6. Schematic representation of one-zone furnace design; 1 - N₂, 2 - steel, 3 - thermal isolation, 4 - pyrophillite, 5 - boron nitride, 6 - graphite, 7 - Ga (liquid), 8 - Al₂O₃; the results of the calculations.

The calculation procedure used the nonuniform grid, defined so that the maximal density is in the region of expected steep temperature gradients. The total number of the grid points was close to 2.5 *10⁴. The solution vector has been attributed a norm which is a sum over all grid points. The iteration procedure was repeated until relative change of the norm of the temperature field was smaller than 10⁻⁵ and the residue norm was smaller than 0.1. The change of the grid density in the region of the steepest gradients has not changed the solution by more than 0.001 of the obtained values.

The results were obtained in the calculation that include or neglects radiative heat exchange. The radiative contribution depends on the detail design of the apparatus. In particular that strongly depends on the approximation of the spiral by the heat source of the shape of the uniform tube. Depending on the details of the exchange between spiral and the internal part of the crucible, the radiation effects can change the temperature of the gallium part by 25 %.

Results of the calculation that include the radiative effects were compared with the temperature measurements in the high pressure growth experiments. The temperature has been measured at the three points of the crucible, close to liquid Ga. The difference between the temperature measured in the experiments and those obtained in our calculation was not higher than 10%.

4. Summary

The results obtained in this work can be summarised as follows:

• • high pressure (of order of 20 kbar) stabilizes the system - it reduces the thermal gradients and slows down the convective motion of the gas

• • radiative energy transfer plays important role in the heat transfer in high pressure crystal growth of GaN

• • scaling hypothesis based methods are capable to estimate the equilibrium and transport properties of nitrogen in pressures up to 20 kbar and temperatures up to 2000K

• • computer methods are able to characterize the temperature distribution in high pressures up to 20 kbar with the precision better than 10%.