Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:50:59.920Z Has data issue: false hasContentIssue false
  • English
  • Français

A parallel root-finding algorithm

Part of: Computer aspects of numerical algorithms Real functions

Published online by Cambridge University Press:  01 December 2015

M. J. P. Nijmeijer
M. J. P. Nijmeijer*
Affiliation:
Heemraadssingel 182D, 3021 DM Rotterdam, The Netherlands email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We present a parallel algorithm to calculate a numerical approximation of a single, isolated root ${\it\alpha}$ of a function 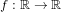$f:\mathbb{R}\rightarrow \mathbb{R}$ which is sufficiently regular at and around ${\it\alpha}$. The algorithm is derivative free and performs one function evaluation on each processor per iteration. It requires at least three processors and can be scaled up to any number of these. The order with which the generated sequence of approximants converges to ${\it\alpha}$ is equal to 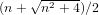$(n+\sqrt{n^{2}+4})/2$ for 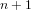$n+1$ processors with 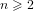$n\geqslant 2$. This assumes that particular combinations of the derivatives of 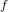$f$ do not vanish at ${\it\alpha}$.

MSC classification

Primary: 26A06: One-variable calculus 39B22: Equations for real functions 65Y05: Parallel computation
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 18 , Issue 1 , 2015 , pp. 713 - 729
Copyright
© The Author 2015 

References

Alefeld, G. E. and Potra, F. A., ‘Some efficient methods for enclosing simple zeros of nonlinear equations’, BIT 32 (1992) no. 2, 334–344.CrossRefGoogle Scholar
Alefeld, G. E., Potra, F. A. and Shi, Y., ‘Algorithm 748: enclosing zeros of continuous functions’, ACM Trans. Math. Software 21 (1995) no. 3, 327–344.CrossRefGoogle Scholar
Amat, S. and Busquier, S., ‘On a higher order secant method’, Appl. Math. Comput. 141 (2003) no. 2–3, 321–329.Google Scholar
Brent, R. P., ‘An algorithm with guaranteed convergence for finding a zero of a function’, Comput. J. 14 (1971) no. 4, 422–425.CrossRefGoogle Scholar
Brent, R., Winograd, S. and Wolfe, P., ‘Optimal iterative processes for root-finding’, Numer. Math. 20 (1973.) 327–341.CrossRefGoogle Scholar
Burden, R. L., Faires, J. D. and Reynolds, A. C., Numerical analysis , 2nd edn (Prindle, Weber and Schmidt, 1981).Google Scholar
Cordero, A., Hueso, J. L., Martínez, E. and Torregrosa, J. R., ‘A family of derivative-free methods with high order of convergence and its application to nonsmooth equations’, Abstr. Appl. Anal. 2012 (2012) Article ID 836901, doi:10.1155/2012/836901.CrossRefGoogle Scholar
Corliss, G. F., ‘Parallel root finding algorithms’, PhD Thesis, Department of Mathematics, Michigan State University, 1974.Google Scholar
Díez, P., ‘A note on the convergence of the secant method for simple and multiple roots’, Appl. Math. Lett. 16 (2003) no. 8, 1211–1215.CrossRefGoogle Scholar
Gal, S. and Miranker, W., ‘Optimal sequential and parallel search for finding a root’, J. Combin. Theory Ser. A 23 (1977) 1–14.CrossRefGoogle Scholar
Ghidouche, K., Couturier, R. and Sider, A., ‘A parallel implementation of the Durand–Kerner algorithm for polynomial root-finding on GPU’, 2014 International Conference on Advanced Networking Distributed Systems and Applications (INDS) (IEEE, 2014) 53–57.CrossRefGoogle Scholar
Hildebrand, F. B., Introduction to numerical analysis , 2nd edn (Dover, 1987).Google Scholar
Ignatova, B., Kyurkchiev, N. and Iliev, A., ‘Multipoint algorithms arising from optimal in the sense of Kung–Traub iterative procedures for numerical solution of nonlinear equations’, Gen. Math. Notes 6 (2011) no. 2, 45–79.Google Scholar
Muller, D. E., ‘A method for solving algebraic equations using an automatic computer’, Mathematical Tables and Other Aids to Computation 10 (1956) 208–215.CrossRefGoogle Scholar
Moore, R. E., Kearfott, R. B. and Cloud, M. J., Introduction to interval analysis (SIAM, 2009).CrossRefGoogle Scholar
Mukai, H., ‘Parallel algorithms for solving systems of nonlinear equations’, Comput. Math. Appl. 7 (1981) 235–250.CrossRefGoogle Scholar
Nijmeijer, M. J. P., ‘A method to accelerate the convergence of the secant algorithm’, Adv. Numer. Anal. 2014 (2014) Article ID 321592, doi:10.1155/2014/321592.Google Scholar
Novak, E., Ritter, K. and Wozniakowski, H., ‘Average case optimality of a hybrid secant-bisection method’, Math. Comp. 64 (1995) no. 212, 1517–1539.CrossRefGoogle Scholar
Pan, V. Y. and Zheng, A.-L., ‘New progress in real and complex polynomial root-finding’, Comput. Math. Appl. 61 (2011) no. 5, 1305–1334.CrossRefGoogle Scholar
Press, W. H., Teukolsky, S. A., Vetterling, W. T. and Flannery, B. P., Numerical recipes: the art of scientific computing , 2nd edn (Cambridge University Press, 2007).Google Scholar
Raydan, M., ‘Exact order of convergence of the Secant method’, J. Optim. Theory Appl. 78 (1993) 541–551.CrossRefGoogle Scholar
Sharma, J. R. and Gupta, P., ‘An efficient family of Traub–Steffensen-type methods for solving systems of nonlinear equations’, Adv. Numer. Anal. 2014 (2014) Article ID 152187, doi:10.1155/2014/152187.Google Scholar
Sidi, A., ‘Unified Treatment of Regula Falsi, Newton–Raphson, Secant, and Steffensen Methods for Nonlinear Equations’, J. Online Math. Appl. 6 (2006), www.maa.org/node/115943.Google Scholar
Sidi, A., ‘Generalization of the Secant method for nonlinear equations’, Appl. Math. E-Notes 8 (2008) 115–123.Google Scholar
Stoer, J. and Bulirsch, R., Introduction to numerical analysis , 3rd edn (Springer, 2002).CrossRefGoogle Scholar
Taher, L. and Elahe, T., ‘On a new efficient Steffensen-like iterative class by applying a suitable self-accelerator parameter’, Sci. World J. 2014 (2014) doi:10.1155/2014/769758.Google Scholar
Traub, J., Iterative methods for the solution of equations (Prentice-Hall, Englewood Cliffs, New Jersey, 1964.).Google Scholar
Kung, H. T. and Traub, J. F., ‘Optimal order of one-point and multipoint iteration’, J. Assoc. Comput. Mach. 21 (1974) no. 4, 643–651.CrossRefGoogle Scholar
Kung, H. T. and Traub, J. F., ‘Optimal order and efficiency for iterations with two evaluations’, SIAM J. Numer. Anal. 13 (1976) no. 1, 84–99.CrossRefGoogle Scholar