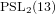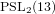Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wilson, Robert A.
2016.
Is the Suzuki group Sz(8) a subgroup of the Monster?.
Bulletin of the London Mathematical Society,
Vol. 48,
Issue. 2,
p.
355.
Wilson, Robert A.
2017.
The uniqueness of PSU 3(8) in the Monster.
Bulletin of the London Mathematical Society,
Vol. 49,
Issue. 5,
p.
877.
Kelsey, Veronica
and
Rowley, Peter
2020.
A note on involution centralizers in black box groups.
Journal of Group Theory,
Vol. 23,
Issue. 2,
p.
287.