Collision times in plasmas are usually defined in connection with the time evolution of the ensemble-averaged scattering angle 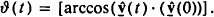. Extrapolating the short-time behaviour ϑshort(t), one obtains the collision time tc by setting ϑshort(tc) = π/2. We have shown with the help of computer simulations that this procedure is ambiguous, as we can clearly distinguish three regimes for ϑ(t). There is always an initial ballistic regime with ϑ(t) ∝ t with dominant pairwise interactions. This lasts up to times α/υth where α is the mean distance between the particles and υth their mean velocity. This is followed by a diffusive regime with ϑ(t) ∝ t½, which is characterized by many small-angle scattering events. Eventually, this diffusion will lead to a uniform distribution of the directions of the velocity. So ϑ(t) will saturate towards π/2 in a third asymptotic regime. For large plasma parameters Γ ≫ 1, this asymptotic behaviour will be modulated by a damped oscillation of ϑ(t) with the plasma frequency. For such strongly coupled plasmas the diffusive regime is suppressed and one observes a direct transition from the initial ballistic to the asymptotic collective regime characterized by the plasma oscillation. Parameters such as the diffusion constant and the transition times are estimated with the help of analytical models.