Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-04T21:03:10.078Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE NON-TRIVIALITY OF THE 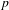$p$ -ADIC ABEL–JACOBI IMAGE OF GENERALISED HEEGNER CYCLES MODULO 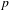$p$ , II: SHIMURA CURVES

Part of: $K$-theory in number theory Discontinuous groups and automorphic forms Arithmetic algebraic geometry Algebraic number theory: global fields

Published online by Cambridge University Press:  07 May 2015

Ashay A. Burungale
Ashay A. Burungale*
Affiliation:
Department of Mathematics, UCLA, Los Angeles, CA 90095-1555, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Generalised Heegner cycles are associated to a pair of an elliptic newform and a Hecke character over an imaginary quadratic extension 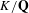$K/\mathbf{Q}$ . The cycles live in a middle-dimensional Chow group of a Kuga–Sato variety arising from an indefinite Shimura curve over the rationals and a self-product of a CM abelian surface. Let 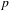$p$ be an odd prime split in 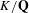$K/\mathbf{Q}$ . We prove the non-triviality of the 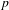$p$ -adic Abel–Jacobi image of generalised Heegner cycles modulo 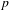$p$ over the 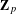$\mathbf{Z}_{p}$ -anticyclotomic extension of  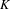$K$ . The result implies the non-triviality of the generalised Heegner cycles in the top graded piece of the coniveau filtration on the Chow group, and proves a higher weight analogue of Mazur’s conjecture. In the case of weight 2, the result provides a refinement of the results of Cornut–Vatsal and Aflalo–Nekovář on the non-triviality of Heegner points over the 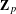$\mathbf{Z}_{p}$ -anticyclotomic extension of  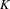$K$ .

Keywords

Shimura curvesmodular formsgeneralised Heegner cyclesp-adic Abel–Jacobi mapHecke stability

MSC classification

Primary: 19F27: Étale cohomology, higher regulators, zeta and $L$-functions 11G18: Arithmetic aspects of modular and Shimura varieties 11R23: Iwasawa theory
Secondary: 11F85: $p$-adic theory, local fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 16 , Issue 1 , February 2017 , pp. 189 - 222
Copyright
© Cambridge University Press 2015. This is a work of the U.S. Government and is not subject to copyright protection in the United States. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aflalo, E. and Nekovář, J., Non-triviality of CM points in ring class field towers (with an appendix by Christophe Cornut), Israel J. Math. 175 (2010), 225–284.Google Scholar
Bertolini, M., Darmon, H. and Prasanna, K., Generalised Heegner cycles and p-adic Rankin L-series, Duke Math. J. 162(6) 1033–1148.Google Scholar
Bertolini, M., Darmon, H. and Prasanna, K., $p$ -adic $L$ -functions and the coniveau filtration on Chow groups, Preprint, 2013 (available at http://www.math.mcgill.ca/darmon/pub/pub.html).Google Scholar
Besser, A., CM cycles over Shimura curves, J. Algebraic Geom. 4(4) (1995), 659–691.Google Scholar
Brakocevic, M., Anticyclotomic p-adic L-function of central critical Rankin–Selberg L-value, Int. Math. Res. Not. IMRN 2011(21) (2011), 4967–5018.Google Scholar
Brooks, E. H., Shimura curves and special values of $p$ -adic $L$ -functions, to appear in IMRN (2014), doi:10.1093/imrn/rnu062.Google Scholar
Burungale, A. and Hsieh, M.-L., The vanishing of 𝜇-invariant of p-adic Hecke L-functions for CM fields, Int. Math. Res. Not. IMRN 2013(5) 1014–1027.CrossRefGoogle Scholar
Burungale, A., On the 𝜇-invariant of the cyclotomic derivative of a Katz p-adic L-function, J. Inst. Math. Jussieu 14(1) (2015), 131–148.Google Scholar
Burungale, A. and Hida, H., $\mathfrak{p}$ -rigidity and Iwasawa $\unicode[STIX]{x1D707}$ -invariants, Preprint, 2014 (available at http://www.math.ucla.edu/∼ashay/).Google Scholar
Burungale, A., $\mathfrak{p}$ -rigidity and $\mathfrak{p}$ -independence of quaternionic modular forms modulo $p$ , Preprint, 2014.Google Scholar
Burungale, A., On the non-triviality of generalised Heegner cycles modulo $p$ , I: modular curves, Preprint, 2014 (available at http://www.math.ucla.edu/∼ashay/).Google Scholar
Burungale, A., Non-triviality of generalised Heegner cycles over anticyclotomic towers: a survey, submitted to the proceedings of the ICTS program ‘ $p$ -adic aspects of modular forms’, 2014.Google Scholar
Burungale, A., On the non-triviality of the $p$ -adic Abel–Jacobi image of generalised Heegner cycles modulo $p$ , III, in progress.Google Scholar
Carayol, H., Sur la mauvaise réduction des courbes de Shimura, Compos. Math. 59(2) (1986), 151–230.Google Scholar
Castella, F., Heegner cycles and higher weight specializations of big Heegner points, Math. Ann. 356 (2013), 1247–1282.Google Scholar
Chai, C.-L., Every ordinary symplectic isogeny class in positive characteristic is dense in the moduli, Invent. Math. 121 (1995), 439–479.CrossRefGoogle Scholar
Chai, C.-L., Families of ordinary abelian varieties: canonical coordinates, $p$ -adic monodromy, Tate-linear subvarieties and Hecke orbits, Preprint, 2003 (available at http://www.math.upenn.edu/∼chai/papers.html).Google Scholar
Chai, C.-L., Hecke orbits as Shimura varieties in positive characteristic, in International Congress of Mathematicians. Vol. II, pp. 295–312 (Eur. Math. Soc., Zurich, 2006).Google Scholar
Cornut, C., Mazur’s conjecture on higher Heegner points, Invent. Math. 148(3) (2002), 495–523.Google Scholar
Cornut, C. and Vatsal, V., CM points and quaternion algebras, Doc. Math. 10 (2005), 263–309.Google Scholar
Cornut, C. and Vatsal, V., Nontriviality of Rankin–Selberg L-functions and CM points, in L-functions and Galois representations, 121–186, London Mathematical Society Lecture Note Series, Volume 320 (Cambridge Univ. Press, Cambridge, 2007).Google Scholar
de Jong, A. J., Homomorphisms of Barsotti–Tate groups and crystals in positive characteristic, Invent. Math. 134 (1998), 301–333.Google Scholar
Fouquet, O., Iwasawa theory of nearly ordinary quaternionic automorphic forms, Compos. Math. 149(3) (2013), 356–416.Google Scholar
Hida, H., p-Adic Automorphic Forms on Shimura Varieties, Springer Monographs in Mathematics (Springer, New York, 2004).Google Scholar
Hida, H., Irreducibility of the Igusa tower, Acta Math. Sin. (Engl. Ser.) 25 (2009), 1–20.Google Scholar
Hida, H., The Iwasawa 𝜇-invariant of p-adic Hecke L-functions, Ann. of Math. (2) 172 (2010), 41–137.Google Scholar
Hida, H., Local indecomposability of Tate modules of non CM abelian varieties with real multiplication, J. Amer. Math. Soc. 26(3) (2013), 853–877.Google Scholar
Hida, H., Elliptic Curves and Arithmetic Invariants, Springer Monographs in Mathematics (Springer, New York, 2013). xviii+449 pp.Google Scholar
Howard, B., Special cohomology classes for modular Galois representations, J. Number Theory 117(2) (2006), 406–438.Google Scholar
Howard, B., Variation of Heegner points in Hida families, Invent. Math. 167(1) (2007), 91–128.Google Scholar
Hsieh, M.-L., On the 𝜇-invariant of anticyclotomic p-adic L-functions for CM fields, J. Reine Angew. Math. 688 (2014), 67–100.Google Scholar
Hsieh, M.-L., Special values of anticyclotomic Rankin-Selbeg L-functions, Doc. Math. 19 (2014), 709–767.CrossRefGoogle Scholar
Jetchev, D., Skinner, C. and Wan, X., The Birch–Swinnerton–Dyer Formula For Elliptic Curves of Analytic Rank One and Main Conjectures, in preparation.Google Scholar
Katz, N. M., p-adic L-functions for CM fields, Invent. Math. 49(3) (1978), 199–297.Google Scholar
Katz, N. M., Serre–Tate local moduli, in Algebraic Surfaces (Orsay, 1976–78), Lecture Notes in Mathematics 868, pp. 138–202 (Springer-Verlag, New York, 1981).Google Scholar
Liu, Y., Zhang, S. and Zhang, W., On $p$ -adic Waldspurger formula, Preprint, 2014 (available at http://www.math.mit.edu/∼liuyf/).Google Scholar
Mazur, B., Modular curves and arithmetic, in Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Warsaw, 1983), pp. 185–211 (PWN, Warsaw, 1984).Google Scholar
Nekovář, J., Kolyvagin’s method for Chow groups of Kuga–Sato varieties, Invent. Math. 107(1) (1992), 99–125.Google Scholar
Nekovář, J., On the parity of ranks of Selmer groups. II, C. R. Math. Acad. Sci. Paris I 332(2) (2001), 99–104.Google Scholar
Nekovář, J., Growth of Selmer groups of Hilbert modular forms over ring class fields, Ann. Sci. Éc. Norm. Supér. (4) 41(6) (2008), 1003–1022.Google Scholar
Nekovář, J., On the parity of ranks of Selmer groups. IV (with an appendix by Jean-Pierre Wintenberger), Compos. Math. 145(6) (2009), 1351–1359.Google Scholar
Prasanna, K., Integrality of a ratio of Petersson norms and level-lowering congruences, Ann. of Math. (2) 163(3) (2006), 901–967.Google Scholar
Rubin, K., p-adic L-functions and rational points on elliptic curves with complex multiplication, Invent. Math. 107(2) (1992), 323–350.Google Scholar
Scholl, A., Motives for modular forms, Invent. Math. 100(2) (1990), 419–430.Google Scholar
Shimura, G., Abelian varieties with complex multiplication and modular functions, Princeton Mathematical Series, 46 (Princeton University Press, Princeton, NJ, 1998).Google Scholar
Vatsal, V., Uniform distribution of Heegner points, Invent. Math. 148 (2002), 1–48.Google Scholar
Vatsal, V., Special values of anticyclotomic L-functions, Duke Math. J. 116 (2003), 219–261.Google Scholar
Vatsal, V., Special values of L-functions modulo p , in International Congress of Mathematicians. Vol. II, pp. 501–514 (Eur. Math. Soc., Zürich, 2006).Google Scholar
Wan, X., Heegner point Kolyvagin system and Iwasawa main conjecture, Preprint, 2014 (available at http://www.math.columbia.edu/∼xw2295).Google Scholar
Yuan, X., Zhang, S. and Zhang, W., The Gross-Zagier formula on Shimura curves, Ann. of Math. Stud. 184 (2013), viii+272 pages.Google Scholar
Zhang, S., Heights of Heegner points on Shimura curves, Ann. of Math. (2) 153(1) (2001), 27–147.Google Scholar