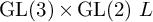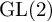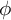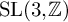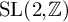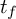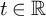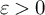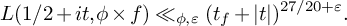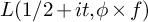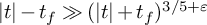1 Introduction
The subconvexity problem of automorphic L-functions on the critical line is a far-reaching problem in number theory and has been a driving force for the development of new techniques and methods. The principal aim is to prove bounds for a given L-function that are better than what the functional equation together with the Phragmén–Lindelöf convexity principle would imply (see, e.g. [Reference Iwaniec and Kowalski22]). For the
![]() $\operatorname {GL}(1)$
case, that is, the Riemann zeta function and Dirichlet L-functions, subconvexity bounds have been known for a long time thanks to Weyl [Reference Weyl47] and Burgess [Reference Burgess8]. In the last several decades, many cases of
$\operatorname {GL}(1)$
case, that is, the Riemann zeta function and Dirichlet L-functions, subconvexity bounds have been known for a long time thanks to Weyl [Reference Weyl47] and Burgess [Reference Burgess8]. In the last several decades, many cases of
![]() $\operatorname {GL}(2) L$
-functions, including the
$\operatorname {GL}(2) L$
-functions, including the
![]() $\operatorname {GL}(2)\times \operatorname {GL}(2)$
Rankin–Selberg L-functions and the triple product L-functions, have been treated (see e.g. Michel–Venkatesh [Reference Michel and Venkatesh36] and the references therein). In recent years, people have made progress on
$\operatorname {GL}(2)\times \operatorname {GL}(2)$
Rankin–Selberg L-functions and the triple product L-functions, have been treated (see e.g. Michel–Venkatesh [Reference Michel and Venkatesh36] and the references therein). In recent years, people have made progress on
![]() $\operatorname {GL}(3)$
L-functions and
$\operatorname {GL}(3)$
L-functions and
![]() $\operatorname {GL}(3)\times \operatorname {GL}(2)$
Rankin–Selberg L-functions (see, e.g. [Reference Blomer4, Reference Blomer and Buttcane5, Reference Huang17, Reference Huang and Xu19, Reference Kumar28, Reference Li30, Reference Lin31, Reference Munshi38, Reference Munshi39, Reference Munshi40, Reference Sharma44]). In this paper, we consider uniform bounds for
$\operatorname {GL}(3)\times \operatorname {GL}(2)$
Rankin–Selberg L-functions (see, e.g. [Reference Blomer4, Reference Blomer and Buttcane5, Reference Huang17, Reference Huang and Xu19, Reference Kumar28, Reference Li30, Reference Lin31, Reference Munshi38, Reference Munshi39, Reference Munshi40, Reference Sharma44]). In this paper, we consider uniform bounds for
![]() $\operatorname {GL}(3)\times \operatorname {GL}(2)$
Rankin–Selberg L-functions on the critical line in both
$\operatorname {GL}(3)\times \operatorname {GL}(2)$
Rankin–Selberg L-functions on the critical line in both
![]() $\operatorname {GL}(2)$
spectral aspect and t aspect.
$\operatorname {GL}(2)$
spectral aspect and t aspect.
Let
![]() $\phi $
be a Hecke–Maass cusp form of type
$\phi $
be a Hecke–Maass cusp form of type
![]() $(\nu _1,\nu _2)$
for
$(\nu _1,\nu _2)$
for
![]() $\operatorname {SL}(3,\mathbb {Z})$
with normalized Fourier coefficients
$\operatorname {SL}(3,\mathbb {Z})$
with normalized Fourier coefficients
![]() $A(m,n)$
[Reference Goldfeld12]. The L-function of
$A(m,n)$
[Reference Goldfeld12]. The L-function of
![]() $\phi $
is defined as
$\phi $
is defined as
 $$\begin{align*}L(s,\phi) = \sum_{n\geq1} \frac{A(1,n)}{n^s}, \quad \operatorname{Re}(s)>1. \end{align*}$$
$$\begin{align*}L(s,\phi) = \sum_{n\geq1} \frac{A(1,n)}{n^s}, \quad \operatorname{Re}(s)>1. \end{align*}$$
Let
![]() $f\in \mathcal {B}_0(1)$
be a Hecke–Maass cusp form with the spectral parameter
$f\in \mathcal {B}_0(1)$
be a Hecke–Maass cusp form with the spectral parameter
![]() $t_f$
for
$t_f$
for
![]() $\operatorname {SL}(2,\mathbb {Z})$
with normalized Fourier coefficients
$\operatorname {SL}(2,\mathbb {Z})$
with normalized Fourier coefficients
![]() $\lambda _f(n)$
. The L-function of f is defined by
$\lambda _f(n)$
. The L-function of f is defined by
 $$\begin{align*}L(s,f) = \sum_{n\geq1} \frac{\lambda_f(n)}{n^s}, \quad \operatorname{Re}(s)>1. \end{align*}$$
$$\begin{align*}L(s,f) = \sum_{n\geq1} \frac{\lambda_f(n)}{n^s}, \quad \operatorname{Re}(s)>1. \end{align*}$$
The
![]() $\operatorname {GL}(3)\times \operatorname {GL}(2)$
Rankin–Selberg L-function is defined as
$\operatorname {GL}(3)\times \operatorname {GL}(2)$
Rankin–Selberg L-function is defined as
 $$\begin{align*}L(s,\phi\times f) = \sum_{m\geq1}\sum_{n\geq1} \frac{A(m,n)\lambda_f(n)}{(m^2n)^s}, \quad \operatorname{Re}(s)>1. \end{align*}$$
$$\begin{align*}L(s,\phi\times f) = \sum_{m\geq1}\sum_{n\geq1} \frac{A(m,n)\lambda_f(n)}{(m^2n)^s}, \quad \operatorname{Re}(s)>1. \end{align*}$$
Those L-functions have analytic continuation to the whole complex plane. Let
![]() $t\in \mathbb {R}$
. We consider bounds for
$t\in \mathbb {R}$
. We consider bounds for
![]() $L(1/2+it,\phi \times f)$
as t or
$L(1/2+it,\phi \times f)$
as t or
![]() $t_f$
or both go to infinity. The Phragmén–Lindelöf principle implies the convexity bounds
$t_f$
or both go to infinity. The Phragmén–Lindelöf principle implies the convexity bounds
The Riemann hypothesis for
![]() $L(s,\phi \times f)$
implies the Lindelöf hypothesis, that is,
$L(s,\phi \times f)$
implies the Lindelöf hypothesis, that is,
Li [Reference Li30] proved the first subconvexity bounds for
![]() $L(1/2,\phi \times f)$
in the
$L(1/2,\phi \times f)$
in the
![]() $\operatorname {GL}(2)$
spectral aspect when
$\operatorname {GL}(2)$
spectral aspect when
![]() $\phi $
is self-dual. There have been several improvements (see, e.g. [Reference McKee, Sun and Ye34]) and generalizations (see, e.g. [Reference Blomer4, Reference Huang17]). In those papers, the moment method for a family of L-functions is used to prove an individual subconvexity bound for one L-function. To make this work, one needs nonnegativity of L-values, and hence, we have the assumption that
$\phi $
is self-dual. There have been several improvements (see, e.g. [Reference McKee, Sun and Ye34]) and generalizations (see, e.g. [Reference Blomer4, Reference Huang17]). In those papers, the moment method for a family of L-functions is used to prove an individual subconvexity bound for one L-function. To make this work, one needs nonnegativity of L-values, and hence, we have the assumption that
![]() $\phi $
is self-dual and this only works for central L-values (at the center
$\phi $
is self-dual and this only works for central L-values (at the center
![]() $1/2$
).
$1/2$
).
Munshi [Reference Munshi38] proved, for the first time, subconvexity bounds for generic
![]() $\operatorname {GL}(3) L$
-functions by applying a delta method. Recently, Munshi [Reference Munshi40] extended his method to prove the first subconvexity for
$\operatorname {GL}(3) L$
-functions by applying a delta method. Recently, Munshi [Reference Munshi40] extended his method to prove the first subconvexity for
![]() $\mathrm GL (3)\times GL (2) \ L$
-functions,
$\mathrm GL (3)\times GL (2) \ L$
-functions,
This was improved by Lin–Sun [Reference Lin and Sun32], and they got
![]() $L(1/2+it,\phi \times f) \ll _{\phi ,f,\varepsilon } (1+|t|)^{27/20+\varepsilon }.$
Based on the work of Munshi [Reference Munshi40], Kumar [Reference Kumar28] was able to use the DFI (Duke–Friedlander–Iwaniec) delta method to prove
$L(1/2+it,\phi \times f) \ll _{\phi ,f,\varepsilon } (1+|t|)^{27/20+\varepsilon }.$
Based on the work of Munshi [Reference Munshi40], Kumar [Reference Kumar28] was able to use the DFI (Duke–Friedlander–Iwaniec) delta method to prove
without the assumption that
![]() $\phi $
is self-dual.
$\phi $
is self-dual.
It is interesting and challenging to prove uniform bounds in terms of both
![]() $t_f$
and t. For the
$t_f$
and t. For the
![]() $\operatorname {GL}(2)$
case, Jutila–Motohashi [Reference Jutila and Motohashi23] proved uniform bounds for
$\operatorname {GL}(2)$
case, Jutila–Motohashi [Reference Jutila and Motohashi23] proved uniform bounds for
![]() $L(s,f)$
on the critical line by the moment method, getting
$L(s,f)$
on the critical line by the moment method, getting
In [Reference Jutila and Motohashi24], Jutila and Motohashi extended their method to show some uniform bounds for
![]() $\operatorname {GL}(2)\times \operatorname {GL}(2) \ L$
-functions. More precisely, they proved
$\operatorname {GL}(2)\times \operatorname {GL}(2) \ L$
-functions. More precisely, they proved
 $$\begin{align*}L(1/2+it,g\times f) \ll_{g,\varepsilon} \left\{ \begin{array}{ll} t_f^{2/3+\varepsilon}, & \textrm{for } 0\leq t\ll t_f^{2/3},\\[2pt] t_f^{1/2+\varepsilon}t^{1/4}, & \textrm{for } t_f^{2/3}\leq t\ll t_f,\\[2pt] t^{3/4+\varepsilon}, & \textrm{for } t_f \ll t\ll t_f^{3/2-\varepsilon}, \end{array} \right. \end{align*}$$
$$\begin{align*}L(1/2+it,g\times f) \ll_{g,\varepsilon} \left\{ \begin{array}{ll} t_f^{2/3+\varepsilon}, & \textrm{for } 0\leq t\ll t_f^{2/3},\\[2pt] t_f^{1/2+\varepsilon}t^{1/4}, & \textrm{for } t_f^{2/3}\leq t\ll t_f,\\[2pt] t^{3/4+\varepsilon}, & \textrm{for } t_f \ll t\ll t_f^{3/2-\varepsilon}, \end{array} \right. \end{align*}$$
where
![]() $f,g$
are Hecke–Maass cusp forms for
$f,g$
are Hecke–Maass cusp forms for
![]() $\operatorname {SL}(2,\mathbb {Z})$
. Their method can not cover all cases of t and
$\operatorname {SL}(2,\mathbb {Z})$
. Their method can not cover all cases of t and
![]() $t_f$
. It seems that it is very hard to extend Jutila–Motohashi’s method to solve the uniform bound problem for high degree L-functions, such as
$t_f$
. It seems that it is very hard to extend Jutila–Motohashi’s method to solve the uniform bound problem for high degree L-functions, such as
![]() $L(1/2+it,\phi \times f)$
. In this paper, we find a way to prove uniform bounds for
$L(1/2+it,\phi \times f)$
. In this paper, we find a way to prove uniform bounds for
![]() $L(1/2+it,\phi \times f)$
for any fixed
$L(1/2+it,\phi \times f)$
for any fixed
![]() $\phi $
. We will use the DFI delta method. In fact, one can also solve the uniform bound problem for
$\phi $
. We will use the DFI delta method. In fact, one can also solve the uniform bound problem for
![]() $\operatorname {GL}(2)\times \operatorname {GL}(2) \ L$
-functions by using our method (together with ideas in [Reference Acharya, Sharma and Singh1]) which may prove uniform bounds for any real t and
$\operatorname {GL}(2)\times \operatorname {GL}(2) \ L$
-functions by using our method (together with ideas in [Reference Acharya, Sharma and Singh1]) which may prove uniform bounds for any real t and
![]() $t_f$
. Our key novelty is the treatment of integral transforms after applying summation formulas, which allows us to deal with the case that both t and
$t_f$
. Our key novelty is the treatment of integral transforms after applying summation formulas, which allows us to deal with the case that both t and
![]() $t_f$
are large. The main result in this paper is the following subconvexity bounds.
$t_f$
are large. The main result in this paper is the following subconvexity bounds.
Theorem 1.1. With the notation as above. Let
![]() $t\in \mathbb {R}$
. Then if
$t\in \mathbb {R}$
. Then if
![]() $||t|-t_f|\geq (|t|+t_f)^{5/6}$
, then we have
$||t|-t_f|\geq (|t|+t_f)^{5/6}$
, then we have
and if
![]() $(|t|+t_f)^{3/5} \leq ||t|-t_f|\leq (|t|+t_f)^{5/6}$
, then we have
$(|t|+t_f)^{3/5} \leq ||t|-t_f|\leq (|t|+t_f)^{5/6}$
, then we have
In particular, we have the following bound
Remark 1.2. The bound (1.2) is uniformly subconvex on
![]() $||t|-t_f|\geq (|t|+t_f)^{4/5+\varepsilon }$
. Our result is new even when
$||t|-t_f|\geq (|t|+t_f)^{4/5+\varepsilon }$
. Our result is new even when
![]() $t=0$
and
$t=0$
and
![]() $t_f\rightarrow \infty $
, which improves Kumar’s result in [Reference Kumar28]. The improvement comes from our treatment of the weight functions after applying summation formulas (see Sections 4 and 5). We also avoid the use of the “conductor lowering trick” of Munshi [Reference Kumar28, Reference Munshi38, Reference Munshi40] as in [Reference Aggarwal2, Reference Huang18, Reference Lin and Sun32]. Note that in this case, our subconvexity bounds are as strong as the case
$t_f\rightarrow \infty $
, which improves Kumar’s result in [Reference Kumar28]. The improvement comes from our treatment of the weight functions after applying summation formulas (see Sections 4 and 5). We also avoid the use of the “conductor lowering trick” of Munshi [Reference Kumar28, Reference Munshi38, Reference Munshi40] as in [Reference Aggarwal2, Reference Huang18, Reference Lin and Sun32]. Note that in this case, our subconvexity bounds are as strong as the case
![]() $t_f\ll 1$
and
$t_f\ll 1$
and
![]() $t\rightarrow \infty $
.
$t\rightarrow \infty $
.
Remark 1.3. By the functional equation of
![]() $L(s,\phi \times f)$
, we can assume
$L(s,\phi \times f)$
, we can assume
![]() $t\geq 0$
in the proof. The uniform bound (1.2) is a consequence of the subconvexity bounds in Theorem 1.1 and the convexity bound (1.1) if
$t\geq 0$
in the proof. The uniform bound (1.2) is a consequence of the subconvexity bounds in Theorem 1.1 and the convexity bound (1.1) if
![]() $|t_f-t|\leq (t_f+|t|)^{3/5+\varepsilon }$
(see Section 2.2 for more details). If
$|t_f-t|\leq (t_f+|t|)^{3/5+\varepsilon }$
(see Section 2.2 for more details). If
![]() $ |t_f-t|\leq (t_f+|t|)^{1-\varepsilon }$
, then we have the conductor drop phenomenon, which makes the subconvexity problem even harder. However, our result still gives subconvexity bounds when
$ |t_f-t|\leq (t_f+|t|)^{1-\varepsilon }$
, then we have the conductor drop phenomenon, which makes the subconvexity problem even harder. However, our result still gives subconvexity bounds when
![]() $|t_f-t| \geq (t_f+|t|)^{3/5+\varepsilon } $
. One may improve our results when
$|t_f-t| \geq (t_f+|t|)^{3/5+\varepsilon } $
. One may improve our results when
![]() $|t_f-t|\leq (t_f+|t|)^{1-\varepsilon }$
by more careful analysis of the integrals in the case
$|t_f-t|\leq (t_f+|t|)^{1-\varepsilon }$
by more careful analysis of the integrals in the case
![]() $|t_f-t|^{1-\varepsilon } \ll \frac {NX}{PQ} \ll (t_f+|t|)^{1-\varepsilon }$
(see Lemmas 4.2 and 5.3 below).
$|t_f-t|^{1-\varepsilon } \ll \frac {NX}{PQ} \ll (t_f+|t|)^{1-\varepsilon }$
(see Lemmas 4.2 and 5.3 below).
Remark 1.4. The method in this paper should work for both holomorphic and Maass forms. In this paper, we focus on the Hecke–Maass cusp form case, as Kumar [Reference Kumar28] gave details for holomorphic forms. Let
![]() $f\in H_k(1)$
be a weight k holomorphic Hecke cusp form for
$f\in H_k(1)$
be a weight k holomorphic Hecke cusp form for
![]() $\operatorname {SL}(2,\mathbb {Z})$
. Then our techniques may yield
$\operatorname {SL}(2,\mathbb {Z})$
. Then our techniques may yield
Remark 1.5. One can combine our ideas here with the method in Huang–Xu [Reference Huang and Xu19] to prove hybrid subconvexity bounds for twists of
![]() $\operatorname {GL}(3)\times \operatorname {GL}(2) \ L$
-functions in the spectral, t, and conductor aspects (see [Reference Huang and Xu19] and the references therein for more background on such hybrid bounds). Let
$\operatorname {GL}(3)\times \operatorname {GL}(2) \ L$
-functions in the spectral, t, and conductor aspects (see [Reference Huang and Xu19] and the references therein for more background on such hybrid bounds). Let
![]() $\phi $
be a Hecke–Maass cusp form for
$\phi $
be a Hecke–Maass cusp form for
![]() $\operatorname {SL}(3,\mathbb {Z})$
and f a Hecke–Maass cusp form with the spectral parameter
$\operatorname {SL}(3,\mathbb {Z})$
and f a Hecke–Maass cusp form with the spectral parameter
![]() $t_f$
for
$t_f$
for
![]() $\operatorname {SL}(2,\mathbb {Z})$
. For
$\operatorname {SL}(2,\mathbb {Z})$
. For
![]() $t\in \mathbb {R}$
and
$t\in \mathbb {R}$
and
![]() $\chi $
a primitive Dirichlet character modulo prime M, our techniques should yield
$\chi $
a primitive Dirichlet character modulo prime M, our techniques should yield
By taking
![]() $\phi $
the minimal Eisenstein series for
$\phi $
the minimal Eisenstein series for
![]() $\operatorname {SL}(3,\mathbb {Z})$
[Reference Goldfeld12], our techniques should yield
$\operatorname {SL}(3,\mathbb {Z})$
[Reference Goldfeld12], our techniques should yield
1.1 Sketch of the proof
In this sketch, we assume
![]() $t+t_f = T \asymp t-t_f$
and
$t+t_f = T \asymp t-t_f$
and
![]() $t\geq 0$
. We want to prove that
$t\geq 0$
. We want to prove that
![]() $L(1/2+it,\phi \times f) \ll _{\phi ,\varepsilon } T^{27/20+\varepsilon }$
. By using the approximate functional equation, we are led to consider the following sum
$L(1/2+it,\phi \times f) \ll _{\phi ,\varepsilon } T^{27/20+\varepsilon }$
. By using the approximate functional equation, we are led to consider the following sum
 $$\begin{align*}\sum_{n\geq1} A(1,n) \lambda_f(n) n^{-it} V\left(\frac{n}{N}\right), \end{align*}$$
$$\begin{align*}\sum_{n\geq1} A(1,n) \lambda_f(n) n^{-it} V\left(\frac{n}{N}\right), \end{align*}$$
for some smooth function V supported in
![]() $[1, 2]$
and satisfying
$[1, 2]$
and satisfying
![]() $V^{(j)}(x) \ll _j 1$
. Hence, to establish subconvexity, we need to show cancellation in the above sum for
$V^{(j)}(x) \ll _j 1$
. Hence, to establish subconvexity, we need to show cancellation in the above sum for
![]() $N\ll T^{3+\varepsilon }$
.
$N\ll T^{3+\varepsilon }$
.
Our first step is to follow Munshi [Reference Munshi40]. We apply the delta method (see Lemma 2.6 below) directly to the above sum as a device for separation of the oscillation of the Fourier coefficients
![]() $A(1,n)$
and
$A(1,n)$
and
![]() $\lambda _f(n) n^{-it}$
, arriving at (we only consider the generic terms in this sketch)
$\lambda _f(n) n^{-it}$
, arriving at (we only consider the generic terms in this sketch)
 $$ \begin{align*} & \frac{1}{Q}\sum_{\substack{q\asymp Q}} \int_{x\asymp 1} \;\frac{1}{q}\; \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} \sum_{n\asymp N} A(1,n) e\left(\frac{-an}{q}\right) e\left(\frac{-nx}{qQ}\right) \\ & \hskip 90pt \cdot \sum_{\substack{m\asymp N}} \lambda_f(m) e\left(\frac{m a}{q}\right) e\left(\frac{m x}{qQ}\right) m^{-it} \mathrm{d}x. \end{align*} $$
$$ \begin{align*} & \frac{1}{Q}\sum_{\substack{q\asymp Q}} \int_{x\asymp 1} \;\frac{1}{q}\; \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} \sum_{n\asymp N} A(1,n) e\left(\frac{-an}{q}\right) e\left(\frac{-nx}{qQ}\right) \\ & \hskip 90pt \cdot \sum_{\substack{m\asymp N}} \lambda_f(m) e\left(\frac{m a}{q}\right) e\left(\frac{m x}{qQ}\right) m^{-it} \mathrm{d}x. \end{align*} $$
Here,
![]() $Q=\sqrt {\frac {N}{K}}$
for some
$Q=\sqrt {\frac {N}{K}}$
for some
![]() $1\ll K= o(T)$
. In fact, we have smooth weights for the sums over m and n and the integral over x. Note that here, we also avoid the use of the “conductor lowering trick” in [Reference Munshi40]. The trivial bound is
$1\ll K= o(T)$
. In fact, we have smooth weights for the sums over m and n and the integral over x. Note that here, we also avoid the use of the “conductor lowering trick” in [Reference Munshi40]. The trivial bound is
![]() $O(N^2)$
, so we need to save N plus a little more.
$O(N^2)$
, so we need to save N plus a little more.
Now, it is standard to apply the Voronoi summation formulas for both m-sum and n-sum above. We proceed as follows. The dual n-sum (after applying Voronoi) was treated in [Reference Huang18], and we get
 $$\begin{align*}q \sum_{\pm} \sum_{n_1|q} \sum_{n_2=1}^{\infty} \frac{A(n_2,n_1)}{n_1n_2} S\left(-\bar{a},\pm n_2;\frac{q}{n_1}\right) \Psi_x^{\pm}\left(\frac{n_1^2n_2}{q^3}\right), \end{align*}$$
$$\begin{align*}q \sum_{\pm} \sum_{n_1|q} \sum_{n_2=1}^{\infty} \frac{A(n_2,n_1)}{n_1n_2} S\left(-\bar{a},\pm n_2;\frac{q}{n_1}\right) \Psi_x^{\pm}\left(\frac{n_1^2n_2}{q^3}\right), \end{align*}$$
for certain weight function
![]() $\Psi _x^{\pm }$
. Here,
$\Psi _x^{\pm }$
. Here,
![]() $S(a,b;c)$
is the Kloosterman sum and
$S(a,b;c)$
is the Kloosterman sum and
![]() $\bar {a} a\equiv 1 \pmod {q/n_1}$
. The sum over n has “conductor”
$\bar {a} a\equiv 1 \pmod {q/n_1}$
. The sum over n has “conductor”
![]() $(\frac {N}{Q^2}Q)^3=N^3/Q^3$
, and hence, the length of the dual sum is
$(\frac {N}{Q^2}Q)^3=N^3/Q^3$
, and hence, the length of the dual sum is
![]() $N^2/Q^3$
. By using the stationary phase method, in the generic case (assuming
$N^2/Q^3$
. By using the stationary phase method, in the generic case (assuming
![]() $n_1=1$
), this becomes
$n_1=1$
), this becomes
 $$\begin{align*}\frac{N^{3/2}}{Q^2} \sum_{\substack{ n_2 \asymp N^2/Q^3}} \frac{A(n_2,1)}{n_2} S\left(-\bar{a},\pm n_2;q\right) e\left( \pm 2 \frac{n_2^{1/2} Q^{1/2}}{q x^{1/2}} \right). \end{align*}$$
$$\begin{align*}\frac{N^{3/2}}{Q^2} \sum_{\substack{ n_2 \asymp N^2/Q^3}} \frac{A(n_2,1)}{n_2} S\left(-\bar{a},\pm n_2;q\right) e\left( \pm 2 \frac{n_2^{1/2} Q^{1/2}}{q x^{1/2}} \right). \end{align*}$$
By the square root cancellation of the Kloosterman sums, we save
![]() $N/(\frac {N^{3/2}}{Q^2} Q^{1/2}) = \frac {Q^{3/2}}{N^{1/2}}$
in this step. Note that we have two oscillatory factors of x which have different exponents for x. So it is a good place to apply the stationary phase method for the x-integral, and this will save
$N/(\frac {N^{3/2}}{Q^2} Q^{1/2}) = \frac {Q^{3/2}}{N^{1/2}}$
in this step. Note that we have two oscillatory factors of x which have different exponents for x. So it is a good place to apply the stationary phase method for the x-integral, and this will save
![]() $\frac {N^{1/2}}{Q}$
. Now, we arrive at
$\frac {N^{1/2}}{Q}$
. Now, we arrive at
 $$ \begin{align} \frac{1}{Q}\sum_{\substack{q\asymp Q}} \frac{1}{q} \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} \frac{N}{Q} \!\sum_{\substack{ n_2 \asymp \frac{ N^{2} } {Q^3} }} \!\frac{A(n_2, 1)}{ n_2} S\left(-\bar{a},\pm n_2;q\right) \sum_{\substack{m\asymp N}} \lambda_f(m) e\left(\frac{ma}{q}\right) e\left(\pm 3\frac{m^{1/3} n_2^{1/3} }{q} \right) m^{-it}. \end{align} $$
$$ \begin{align} \frac{1}{Q}\sum_{\substack{q\asymp Q}} \frac{1}{q} \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} \frac{N}{Q} \!\sum_{\substack{ n_2 \asymp \frac{ N^{2} } {Q^3} }} \!\frac{A(n_2, 1)}{ n_2} S\left(-\bar{a},\pm n_2;q\right) \sum_{\substack{m\asymp N}} \lambda_f(m) e\left(\frac{ma}{q}\right) e\left(\pm 3\frac{m^{1/3} n_2^{1/3} }{q} \right) m^{-it}. \end{align} $$
Consider the sum over m, which involves
![]() $\operatorname {GL}(2)$
Fourier coefficients and has conductor
$\operatorname {GL}(2)$
Fourier coefficients and has conductor
![]() $Q^2T^2$
if
$Q^2T^2$
if
![]() $t\pm t_f \asymp T$
. By applying the Voronoi summation formula, a typical term in the dual m-sum is
$t\pm t_f \asymp T$
. By applying the Voronoi summation formula, a typical term in the dual m-sum is
 $$\begin{align*}q \sum_{m\geq1} \frac{ \lambda_{f}(m) }{m} e\left(\frac{\bar{a} m}{q}\right) G \left(\frac{m}{q^2} \right), \end{align*}$$
$$\begin{align*}q \sum_{m\geq1} \frac{ \lambda_{f}(m) }{m} e\left(\frac{\bar{a} m}{q}\right) G \left(\frac{m}{q^2} \right), \end{align*}$$
where
 $$\begin{align*}\gamma_2 (-1/2+i\tau-it) = \frac{\Gamma(\frac{1/2+i\tau-iT}{2})\Gamma(\frac{1/2+i\tau-iT'}{2})} {\Gamma(\frac{1/2-i\tau+iT}{2})\Gamma(\frac{1/2-i\tau+iT'}{2})} + \frac{\Gamma(\frac{3/2+i\tau-iT}{2})\Gamma(\frac{3/2+i\tau-iT'}{2})} {\Gamma(\frac{3/2-i\tau+iT}{2})\Gamma(\frac{3/2-i\tau+iT'}{2})}, \end{align*}$$
$$\begin{align*}\gamma_2 (-1/2+i\tau-it) = \frac{\Gamma(\frac{1/2+i\tau-iT}{2})\Gamma(\frac{1/2+i\tau-iT'}{2})} {\Gamma(\frac{1/2-i\tau+iT}{2})\Gamma(\frac{1/2-i\tau+iT'}{2})} + \frac{\Gamma(\frac{3/2+i\tau-iT}{2})\Gamma(\frac{3/2+i\tau-iT'}{2})} {\Gamma(\frac{3/2-i\tau+iT}{2})\Gamma(\frac{3/2-i\tau+iT'}{2})}, \end{align*}$$
 $$\begin{align*}\tilde{g}(s) = \int_{0}^{\infty} g(u) u^{s-1}\mathrm{d} u , \quad g(u)= e\left(\pm 3\frac{u^{1/3} n_2^{1/3} }{q} \right) u^{-it} W\left(\frac{u}{N}\right) , \end{align*}$$
$$\begin{align*}\tilde{g}(s) = \int_{0}^{\infty} g(u) u^{s-1}\mathrm{d} u , \quad g(u)= e\left(\pm 3\frac{u^{1/3} n_2^{1/3} }{q} \right) u^{-it} W\left(\frac{u}{N}\right) , \end{align*}$$
for some nice smooth function W. Here, we introduce two new parameters
The analysis of
![]() $G(y)$
is the main part of this paper. Note that we also have some other expressions for
$G(y)$
is the main part of this paper. Note that we also have some other expressions for
![]() $G(y)$
. For example, the one with Bessel functions (see Lemma 2.4), which will also be used in the nongeneric cases to truncate the dual m-sum. In our generic case, by applying the stationary phase method for
$G(y)$
. For example, the one with Bessel functions (see Lemma 2.4), which will also be used in the nongeneric cases to truncate the dual m-sum. In our generic case, by applying the stationary phase method for
![]() $\tilde {g}(1/2-i\tau +it)$
, we get a nice asymptotic formula of this and restrict to
$\tilde {g}(1/2-i\tau +it)$
, we get a nice asymptotic formula of this and restrict to
![]() $\tau \asymp N/Q^2=K = o(T)$
. With the assumption
$\tau \asymp N/Q^2=K = o(T)$
. With the assumption
![]() $T'\asymp T$
, we can use the Stirling’s formula to get a good approximation of
$T'\asymp T$
, we can use the Stirling’s formula to get a good approximation of
![]() $\gamma _2 (-1/2+i\tau -it)$
. Finally, the stationary phase method can be applied to the
$\gamma _2 (-1/2+i\tau -it)$
. Finally, the stationary phase method can be applied to the
![]() $\tau $
-integral, which restrict y to
$\tau $
-integral, which restrict y to
![]() $(yN)^{1/2}\asymp T$
. By doing these, we will not lose anything in this integral transform. This is the key to our improvement (cf. [Reference Kumar28, Section 7]). More importantly, our method does not really depend on the sizes of t and
$(yN)^{1/2}\asymp T$
. By doing these, we will not lose anything in this integral transform. This is the key to our improvement (cf. [Reference Kumar28, Section 7]). More importantly, our method does not really depend on the sizes of t and
![]() $t_f$
but instead the sizes of T and
$t_f$
but instead the sizes of T and
![]() $T'$
. So as long as
$T'$
. So as long as
![]() $T'$
is not too small compared to T, we may get nontrivial bounds. This is the reason why we can prove a uniform bound. Those arguments show that the length of the dual m-sum is
$T'$
is not too small compared to T, we may get nontrivial bounds. This is the reason why we can prove a uniform bound. Those arguments show that the length of the dual m-sum is
![]() $Q^2T^2/N$
and the size of
$Q^2T^2/N$
and the size of
![]() $G(y)$
is
$G(y)$
is
![]() $O((yN)^{1/2})=O(T)$
. Now (1.3) essentially becomes
$O((yN)^{1/2})=O(T)$
. Now (1.3) essentially becomes
 $$ \begin{align*} \frac{N^{1/2} }{Q} \frac{N}{Q} \sum_{\substack{n_2 \asymp \frac{N^{2}} {Q^3} }} \frac{A(n_2,1)}{n_2} \cdot \sum_{\substack{q\asymp Q}} \;\frac{1}{q} \sum_{\substack{ m\asymp \frac{Q^2T^2}{N} }} \frac{ \lambda_{f}(m) }{m^{1/2}} \left(\frac{m}{q^2}\right)^{it} \mathcal{C}(n_2,m,q) \mathcal{I}(n_2,m,q) , \end{align*} $$
$$ \begin{align*} \frac{N^{1/2} }{Q} \frac{N}{Q} \sum_{\substack{n_2 \asymp \frac{N^{2}} {Q^3} }} \frac{A(n_2,1)}{n_2} \cdot \sum_{\substack{q\asymp Q}} \;\frac{1}{q} \sum_{\substack{ m\asymp \frac{Q^2T^2}{N} }} \frac{ \lambda_{f}(m) }{m^{1/2}} \left(\frac{m}{q^2}\right)^{it} \mathcal{C}(n_2,m,q) \mathcal{I}(n_2,m,q) , \end{align*} $$
where
 $$ \begin{align*} \mathcal{C}(n_2,m,q) = \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} e\left(\frac{\bar{a} m}{q}\right) S\left(-\bar{a},\pm n_2;q\right) \rightsquigarrow q \; e\left( \pm \frac{\bar{m}n_2}{q} \right) \end{align*} $$
$$ \begin{align*} \mathcal{C}(n_2,m,q) = \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} e\left(\frac{\bar{a} m}{q}\right) S\left(-\bar{a},\pm n_2;q\right) \rightsquigarrow q \; e\left( \pm \frac{\bar{m}n_2}{q} \right) \end{align*} $$
and
![]() $\mathcal {I}(n_2,m,q)$
is a certain nice oscillatory function with the phase function of size
$\mathcal {I}(n_2,m,q)$
is a certain nice oscillatory function with the phase function of size
![]() $N/Q^2$
with respect to
$N/Q^2$
with respect to
![]() $n_2$
. Here, for the character sum
$n_2$
. Here, for the character sum
![]() $\mathcal {C}(n_2,m,q)$
, the sum over a becomes a Ramanujan sum. So, typically, we have
$\mathcal {C}(n_2,m,q)$
, the sum over a becomes a Ramanujan sum. So, typically, we have
![]() $\mathcal {C}(n_2,m,q)\ll q$
and we save
$\mathcal {C}(n_2,m,q)\ll q$
and we save
![]() $Q^{1/2}$
. Hence, we save
$Q^{1/2}$
. Hence, we save
![]() $\frac {N}{QT}Q^{1/2} = \frac {N}{Q^{1/2}T}$
from the treatment of the m-sum. So we have saved
$\frac {N}{QT}Q^{1/2} = \frac {N}{Q^{1/2}T}$
from the treatment of the m-sum. So we have saved
![]() $\frac {Q^{3/2}}{N^{1/2}}\cdot \frac {N^{1/2}}{Q}\cdot \frac {N}{Q^{1/2}T}=\frac {N}{T}$
in total, and it remains to save T plus a little extra.
$\frac {Q^{3/2}}{N^{1/2}}\cdot \frac {N^{1/2}}{Q}\cdot \frac {N}{Q^{1/2}T}=\frac {N}{T}$
in total, and it remains to save T plus a little extra.
The next step involves taking Cauchy to get rid of the Fourier coefficients
![]() $A(n_2,1)$
, but this process also squares the amount we need to save, getting (essentially)
$A(n_2,1)$
, but this process also squares the amount we need to save, getting (essentially)
 $$\begin{align*}\frac{1}{T} \frac{N}{Q^{3/2}} \Bigg( \sum_{n_2 \asymp \frac{N^{2}} {Q^3}} \bigg| \sum_{\substack{q\asymp Q}} \sum_{\substack{ m\asymp \frac{Q^2T^2}{N} }} \lambda_{f}(m) e\left( \pm \frac{\bar{m}n_2}{q} \right) \mathcal{I}(n_2,m,q) \bigg|^2 \Bigg)^{1/2}. \end{align*}$$
$$\begin{align*}\frac{1}{T} \frac{N}{Q^{3/2}} \Bigg( \sum_{n_2 \asymp \frac{N^{2}} {Q^3}} \bigg| \sum_{\substack{q\asymp Q}} \sum_{\substack{ m\asymp \frac{Q^2T^2}{N} }} \lambda_{f}(m) e\left( \pm \frac{\bar{m}n_2}{q} \right) \mathcal{I}(n_2,m,q) \bigg|^2 \Bigg)^{1/2}. \end{align*}$$
Opening the absolute value square, we get (essentially)
 $$\begin{align*}\frac{1}{T} \frac{N}{Q^{3/2}} \Bigg( \sum_{\substack{q\asymp Q}} \sum_{\substack{ m\asymp \frac{Q^2T^2}{N} }} \sum_{\substack{q'\asymp Q}} \sum_{\substack{ m'\asymp \frac{Q^2T^2}{N} }} \sum_{n_2 \asymp \frac{N^{2}} {Q^3}}\! e\left( \pm \frac{(\bar{m}q' - \bar{m}'q )n_2}{qq'} \right) \mathcal{I}(n_2,m,q) \overline{\mathcal{I}(n_2,m',q')} \Bigg)^{1/2}. \end{align*}$$
$$\begin{align*}\frac{1}{T} \frac{N}{Q^{3/2}} \Bigg( \sum_{\substack{q\asymp Q}} \sum_{\substack{ m\asymp \frac{Q^2T^2}{N} }} \sum_{\substack{q'\asymp Q}} \sum_{\substack{ m'\asymp \frac{Q^2T^2}{N} }} \sum_{n_2 \asymp \frac{N^{2}} {Q^3}}\! e\left( \pm \frac{(\bar{m}q' - \bar{m}'q )n_2}{qq'} \right) \mathcal{I}(n_2,m,q) \overline{\mathcal{I}(n_2,m',q')} \Bigg)^{1/2}. \end{align*}$$
We now apply the Poisson summation formula on the sum over
![]() $n_2$
modulo
$n_2$
modulo
![]() $qq'$
, arriving at
$qq'$
, arriving at
 $$\begin{align*}\frac{1}{T} \frac{N}{Q^{3/2}} \Bigg( \sum_{\substack{q\asymp Q}} \sum_{\substack{ m\asymp \frac{Q^2T^2}{N} }} \sum_{\substack{q'\asymp Q}} \sum_{\substack{ m'\asymp \frac{Q^2T^2}{N} }} \sum_{n\in \mathbb{Z}} \mathfrak{C}(n,q,q',m,m') \mathfrak{I}(n,q,q',m,m') \Bigg)^{1/2}, \end{align*}$$
$$\begin{align*}\frac{1}{T} \frac{N}{Q^{3/2}} \Bigg( \sum_{\substack{q\asymp Q}} \sum_{\substack{ m\asymp \frac{Q^2T^2}{N} }} \sum_{\substack{q'\asymp Q}} \sum_{\substack{ m'\asymp \frac{Q^2T^2}{N} }} \sum_{n\in \mathbb{Z}} \mathfrak{C}(n,q,q',m,m') \mathfrak{I}(n,q,q',m,m') \Bigg)^{1/2}, \end{align*}$$
where
 $$\begin{align*}\mathfrak{C}(n,q,q',m,m') = \frac{1}{qq'} \sum_{b\bmod{qq'}} e\left( \pm \frac{(\bar{m}q' - \bar{m}'q + n)b}{qq'} \right) , \end{align*}$$
$$\begin{align*}\mathfrak{C}(n,q,q',m,m') = \frac{1}{qq'} \sum_{b\bmod{qq'}} e\left( \pm \frac{(\bar{m}q' - \bar{m}'q + n)b}{qq'} \right) , \end{align*}$$
and
 $$ \begin{align*} \mathfrak{I}(n,q,q',m,m') & = \int_{\mathbb{R}} \mathcal{I}(u,m,q) \overline{\mathcal{I}(u,m',q')} W\left(\frac{u}{N^2/Q^3}\right) e\left( \frac{un}{qq'} \right) \mathrm{d} u \\ & = \frac{N^2}{Q^3} \int_{\mathbb{R}} \mathcal{I}\Big(\frac{N^2}{Q^3}\xi,m,q\Big) \overline{\mathcal{I}\Big(\frac{N^2}{Q^3}\xi,m',q'\Big)} W\left(\xi\right) e\left( \frac{N^2 n}{Q^3 qq'} \xi \right) \mathrm{d} \xi. \end{align*} $$
$$ \begin{align*} \mathfrak{I}(n,q,q',m,m') & = \int_{\mathbb{R}} \mathcal{I}(u,m,q) \overline{\mathcal{I}(u,m',q')} W\left(\frac{u}{N^2/Q^3}\right) e\left( \frac{un}{qq'} \right) \mathrm{d} u \\ & = \frac{N^2}{Q^3} \int_{\mathbb{R}} \mathcal{I}\Big(\frac{N^2}{Q^3}\xi,m,q\Big) \overline{\mathcal{I}\Big(\frac{N^2}{Q^3}\xi,m',q'\Big)} W\left(\xi\right) e\left( \frac{N^2 n}{Q^3 qq'} \xi \right) \mathrm{d} \xi. \end{align*} $$
For the zero frequency (
![]() $n=0$
), the main contribution comes from terms with
$n=0$
), the main contribution comes from terms with
![]() $q=q'$
and
$q=q'$
and
![]() $m=m'$
, in which case, there is no further cancellation in the character sums. So we save
$m=m'$
, in which case, there is no further cancellation in the character sums. So we save
![]() $(Q \frac {Q^2T^2}{N})^{1/2} = \frac {Q^{3/2}T}{N^{1/2}}$
. Hence, the final contribution from the zero frequency is
$(Q \frac {Q^2T^2}{N})^{1/2} = \frac {Q^{3/2}T}{N^{1/2}}$
. Hence, the final contribution from the zero frequency is
![]() $O(N^2/(\frac {N}{T}\frac {Q^{3/2}T}{N^{1/2}})) = O(N^{3/2}/Q^{3/2})$
.
$O(N^2/(\frac {N}{T}\frac {Q^{3/2}T}{N^{1/2}})) = O(N^{3/2}/Q^{3/2})$
.
For the nonzero frequencies (
![]() $n\neq 0$
), the main contribution comes from the terms in generic positions (that is, no restriction to reduce the size of the number of
$n\neq 0$
), the main contribution comes from the terms in generic positions (that is, no restriction to reduce the size of the number of
![]() $q,q',m,m'$
). As mentioned in Munshi [Reference Munshi40], we save more than the usual since the character sum boils down to an additive character. In the generic case, the “conductor” is of the size
$q,q',m,m'$
). As mentioned in Munshi [Reference Munshi40], we save more than the usual since the character sum boils down to an additive character. In the generic case, the “conductor” is of the size
![]() $Q^2 \frac {N}{Q^2}=N$
, and hence, the length of the dual sum is
$Q^2 \frac {N}{Q^2}=N$
, and hence, the length of the dual sum is
![]() $O( \frac {N}{N^2/Q^3})=O(Q^3/N)$
. By the stationary phase method, we save
$O( \frac {N}{N^2/Q^3})=O(Q^3/N)$
. By the stationary phase method, we save
![]() $(\sqrt {N/Q^2})^{1/2}$
in
$(\sqrt {N/Q^2})^{1/2}$
in
![]() $\mathfrak {I}(n,q,q',m,m')$
. We remark that for the nongeneric cases, we will apply
$\mathfrak {I}(n,q,q',m,m')$
. We remark that for the nongeneric cases, we will apply
![]() $L^2$
-norm estimate for
$L^2$
-norm estimate for
![]() $\mathcal {I}(u,m,q)$
instead of the stationary phase method. For the character sums
$\mathcal {I}(u,m,q)$
instead of the stationary phase method. For the character sums
![]() $\mathfrak {C}(n,q,q',m,m')$
, we save
$\mathfrak {C}(n,q,q',m,m')$
, we save
![]() $(Q^2)^{1/2}$
since this is a Ramanujan sum with modulo
$(Q^2)^{1/2}$
since this is a Ramanujan sum with modulo
![]() $qq'$
. So in this case, we save
$qq'$
. So in this case, we save
![]() $(\sqrt {N/Q^2})^{1/2}\cdot (Q^2)^{1/2} \cdot (N/Q^3)^{1/2} = N^{3/4}/Q$
. Hence, the final contribution from the nonzero frequencies is
$(\sqrt {N/Q^2})^{1/2}\cdot (Q^2)^{1/2} \cdot (N/Q^3)^{1/2} = N^{3/4}/Q$
. Hence, the final contribution from the nonzero frequencies is
![]() $O(N^2/(\frac {N}{T} \frac {N^{3/4}}{Q})) = O(N^{1/4} QT)$
.
$O(N^2/(\frac {N}{T} \frac {N^{3/4}}{Q})) = O(N^{1/4} QT)$
.
The best choice is
![]() $Q=\frac {N^{1/2}}{T^{2/5}}$
, which gives a bound
$Q=\frac {N^{1/2}}{T^{2/5}}$
, which gives a bound
![]() $O(N^{1/2}T^{27/20+\varepsilon })$
by using
$O(N^{1/2}T^{27/20+\varepsilon })$
by using
![]() $N\ll T^{3+\varepsilon }$
and hence proves that
$N\ll T^{3+\varepsilon }$
and hence proves that
![]() $L(1/2+it,\phi \times f) \ll _{\phi ,\varepsilon } T^{27/20+\varepsilon }$
.
$L(1/2+it,\phi \times f) \ll _{\phi ,\varepsilon } T^{27/20+\varepsilon }$
.
1.2 Plan for this paper
The rest of this paper is organized as follows. In Section 2, we introduce some notation and present some lemmas that we will need later. The approximate functional equation allows us to reduce the subconvexity problem to estimate certain convolution sums. In Section 3, we apply the delta method to the convolution sums. In Section 4, we apply the Voronoi summation formulas and estimate the integral transforms by the stationary phase method. In Section 5, we apply the Cauchy–Schwarz inequality and Poisson summation formula, and then analyze the character sums and integrals. Then, we deal with the contribution from the zero frequency in Section 6. The contribution from nonzero frequencies is bounded in Sections 7 and 8. Finally, in Section 9, we complete the proof of our main theorem.
Notation. Throughout the paper,
![]() $\varepsilon $
is an arbitrarily small positive number; all of them may be different at each occurrence. The weight functions
$\varepsilon $
is an arbitrarily small positive number; all of them may be different at each occurrence. The weight functions
![]() $U,\ V,\ W$
may also change at each occurrence. As usual,
$U,\ V,\ W$
may also change at each occurrence. As usual,
![]() $e(x)=e^{2\pi i x}$
. We use
$e(x)=e^{2\pi i x}$
. We use
![]() $y\asymp Y$
to mean that
$y\asymp Y$
to mean that
![]() $c_1 Y\leq |y|\leq c_2 Y$
for some positive constants
$c_1 Y\leq |y|\leq c_2 Y$
for some positive constants
![]() $c_1$
and
$c_1$
and
![]() $c_2$
, and
$c_2$
, and
![]() $q\sim P$
means
$q\sim P$
means
![]() $P<q\leq 2P$
.
$P<q\leq 2P$
.
2 Preliminaries
2.1 Automorphic forms
Let
![]() $f\in \mathcal {B}_0(1)$
be a Hecke–Maass cusp form with the spectral parameter
$f\in \mathcal {B}_0(1)$
be a Hecke–Maass cusp form with the spectral parameter
![]() $t_f$
for
$t_f$
for
![]() $\operatorname {SL}(2,\mathbb {Z})$
with the normalized Fourier coefficients
$\operatorname {SL}(2,\mathbb {Z})$
with the normalized Fourier coefficients
![]() $\lambda _f(n)$
. Let
$\lambda _f(n)$
. Let
![]() $\theta _2$
be the bound toward the Ramanujan conjecture, and we have
$\theta _2$
be the bound toward the Ramanujan conjecture, and we have
![]() $\theta _2\leq 7/64$
due to Kim–Sarnak [Reference Kim25]. Rankin–Selberg theory gives (see Iwaniec [Reference Iwaniec21, Lemma 1])
$\theta _2\leq 7/64$
due to Kim–Sarnak [Reference Kim25]. Rankin–Selberg theory gives (see Iwaniec [Reference Iwaniec21, Lemma 1])
Let
![]() $\phi $
be a Hecke–Maass cusp form of type
$\phi $
be a Hecke–Maass cusp form of type
![]() $(\nu _1,\nu _2)$
for
$(\nu _1,\nu _2)$
for
![]() $\operatorname {SL}(3,\mathbb {Z})$
with the normalized Fourier coefficients
$\operatorname {SL}(3,\mathbb {Z})$
with the normalized Fourier coefficients
![]() $A(r,n)$
. Rankin–Selberg theory gives
$A(r,n)$
. Rankin–Selberg theory gives
We record the Hecke relation
 $$\begin{align*}A(r,n) = \sum_{d\mid (r,n)} \mu(d) A\left(\frac{r}{d},1\right) A\left(1,\frac{n}{d}\right) \end{align*}$$
$$\begin{align*}A(r,n) = \sum_{d\mid (r,n)} \mu(d) A\left(\frac{r}{d},1\right) A\left(1,\frac{n}{d}\right) \end{align*}$$
which follows from Möbius inversion and [Reference Goldfeld12, Theorem 6.4.11]. Hence, we have the individual bounds
where
![]() $\theta _3\leq 5/14$
is the bound toward the Ramanujan conjecture on
$\theta _3\leq 5/14$
is the bound toward the Ramanujan conjecture on
![]() $\operatorname {GL}(3)$
([Reference Kim25]). Thus, we have
$\operatorname {GL}(3)$
([Reference Kim25]). Thus, we have
 $$ \begin{align} \sum_{n\sim N} |A(r,n)| \ll \sum_{n_1\mid r^{\infty}} \sum_{\substack{n\sim N/n_1 \\ (n,r)=1}} |A(r,nn_1)| \leq \sum_{n_1\mid r^{\infty}}|A(r,n_1)| \sum_{\substack{n\sim N/n_1 \\ (n,r)=1}} |A(1,n)| \ll r^{\theta_3+\varepsilon} N \end{align} $$
$$ \begin{align} \sum_{n\sim N} |A(r,n)| \ll \sum_{n_1\mid r^{\infty}} \sum_{\substack{n\sim N/n_1 \\ (n,r)=1}} |A(r,nn_1)| \leq \sum_{n_1\mid r^{\infty}}|A(r,n_1)| \sum_{\substack{n\sim N/n_1 \\ (n,r)=1}} |A(1,n)| \ll r^{\theta_3+\varepsilon} N \end{align} $$
and
 $$ \begin{align} \sum_{n\sim N} |A(r,n)|^2 \ll \sum_{n_1\mid r^{\infty}} \sum_{\substack{n\sim N/n_1 \\ (n,r)=1}} |A(r,nn_1)|^2 \leq \sum_{n_1\mid r^{\infty}}|A(r,n_1)|^2 \sum_{\substack{n\sim N/n_1 \\ (n,r)=1}} |A(1,n)|^2 \ll r^{2\theta_3+\varepsilon} N. \end{align} $$
$$ \begin{align} \sum_{n\sim N} |A(r,n)|^2 \ll \sum_{n_1\mid r^{\infty}} \sum_{\substack{n\sim N/n_1 \\ (n,r)=1}} |A(r,nn_1)|^2 \leq \sum_{n_1\mid r^{\infty}}|A(r,n_1)|^2 \sum_{\substack{n\sim N/n_1 \\ (n,r)=1}} |A(1,n)|^2 \ll r^{2\theta_3+\varepsilon} N. \end{align} $$
Those bounds depend on
![]() $\phi $
and
$\phi $
and
![]() $\varepsilon $
. Here, we have used (2.2) and the fact
$\varepsilon $
. Here, we have used (2.2) and the fact
![]() $ \sum _{d\mid r^{\infty }} d^{-\sigma } \ll r^{\varepsilon }, \; \textrm {for } \sigma>0. $
$ \sum _{d\mid r^{\infty }} d^{-\sigma } \ll r^{\varepsilon }, \; \textrm {for } \sigma>0. $
2.2 The approximate functional equation
The Rankin–Selberg L-function
![]() $L(s,\phi \times f)$
has the following functional equation
$L(s,\phi \times f)$
has the following functional equation
where
 $$\begin{align*}\Lambda(s,\phi\times f) = \pi^{-3s} \prod_{j=1}^{3} \prod_{\pm} \Gamma\left(\frac{s-\alpha_j\pm i t_f}{2}\right) L(s,\phi\times f) \end{align*}$$
$$\begin{align*}\Lambda(s,\phi\times f) = \pi^{-3s} \prod_{j=1}^{3} \prod_{\pm} \Gamma\left(\frac{s-\alpha_j\pm i t_f}{2}\right) L(s,\phi\times f) \end{align*}$$
is the completed L-function and
![]() $\epsilon _{\phi \times f}$
is the root number, which has absolute value one. Here,
$\epsilon _{\phi \times f}$
is the root number, which has absolute value one. Here,
![]() $\alpha _j$
are the Langlands parameters of
$\alpha _j$
are the Langlands parameters of
![]() $\phi $
, and
$\phi $
, and
![]() $\tilde \phi $
is the dual form of
$\tilde \phi $
is the dual form of
![]() $\phi $
. We have the following approximate functional equation.
$\phi $
. We have the following approximate functional equation.
Lemma 2.1. Assume
![]() $t\geq 0$
. Let
$t\geq 0$
. Let
![]() $T=t+t_f$
and
$T=t+t_f$
and
![]() $T'=t-t_f$
. Then we have
$T'=t-t_f$
. Then we have
 $$\begin{align*}L(1/2+it,\phi\times f) \ll_{\phi,\varepsilon} T^{\varepsilon} \sup_{ 1 \leq N \leq T^{3/2+\varepsilon}(|T'|+1)^{3/2}} \frac{|S(N)|}{N^{1/2}} + T^{-2021}, \end{align*}$$
$$\begin{align*}L(1/2+it,\phi\times f) \ll_{\phi,\varepsilon} T^{\varepsilon} \sup_{ 1 \leq N \leq T^{3/2+\varepsilon}(|T'|+1)^{3/2}} \frac{|S(N)|}{N^{1/2}} + T^{-2021}, \end{align*}$$
where
![]() $S(N)$
is a sum of the form
$S(N)$
is a sum of the form
 $$\begin{align*}S(N) := \sum_{r\geq1}\sum_{n\geq1} A(r,n) \lambda_f(n) (r^2n)^{-it} V\left(\frac{r^2n}{N}\right) \end{align*}$$
$$\begin{align*}S(N) := \sum_{r\geq1}\sum_{n\geq1} A(r,n) \lambda_f(n) (r^2n)^{-it} V\left(\frac{r^2n}{N}\right) \end{align*}$$
for some smooth function V, such that
![]() $\int _{\mathbb {R}}V(x)\mathrm {d} x=1$
,
$\int _{\mathbb {R}}V(x)\mathrm {d} x=1$
,
![]() $\operatorname {supp} V \subset [1,2]$
, and
$\operatorname {supp} V \subset [1,2]$
, and
![]() $V^{(j)}(x) \ll _j 1$
for any integer
$V^{(j)}(x) \ll _j 1$
for any integer
![]() $j\geq 0$
.
$j\geq 0$
.
Proof. See [Reference Iwaniec and Kowalski22, Section 5.2].
If
![]() $|T'| \leq T^{3/5}$
, then Lemma 2.1 gives
$|T'| \leq T^{3/5}$
, then Lemma 2.1 gives
which is better than (1.2). Hence, to prove Theorem 1.1, we only need to consider the case
![]() $|T'| \geq T^{3/5}$
, which we assume from now on. We will always write
$|T'| \geq T^{3/5}$
, which we assume from now on. We will always write
We first estimate the contribution from large values of r. By (2.1) and (2.4), we have
 $$ \begin{align*} \sum_{r\geq R} & \left|\sum_{n\geq1} A(r,n) \lambda_f(n) (r^2n)^{-it} V\left(\frac{r^2n}{N}\right)\right| \\ & \ll \sum_{ R \leq r \ll \sqrt{N}} \left(\sum_{n\asymp N/r^2} |A(r,n)|^2 \right)^{1/2} \left(\sum_{n\asymp N/r^2} |\lambda_f(n)|^2\right)^{1/2} \\ & \ll \sum_{ R \leq r \ll \sqrt{N}} r^{\theta_3+\varepsilon} \frac{N}{r^2} \ll N \sum_{ R \leq r \ll \sqrt{N}} r^{-23/14+\varepsilon} \ll N^{1/2} T^{3/4+\varepsilon} |T'|^{3/4} R^{-9/14}, \end{align*} $$
$$ \begin{align*} \sum_{r\geq R} & \left|\sum_{n\geq1} A(r,n) \lambda_f(n) (r^2n)^{-it} V\left(\frac{r^2n}{N}\right)\right| \\ & \ll \sum_{ R \leq r \ll \sqrt{N}} \left(\sum_{n\asymp N/r^2} |A(r,n)|^2 \right)^{1/2} \left(\sum_{n\asymp N/r^2} |\lambda_f(n)|^2\right)^{1/2} \\ & \ll \sum_{ R \leq r \ll \sqrt{N}} r^{\theta_3+\varepsilon} \frac{N}{r^2} \ll N \sum_{ R \leq r \ll \sqrt{N}} r^{-23/14+\varepsilon} \ll N^{1/2} T^{3/4+\varepsilon} |T'|^{3/4} R^{-9/14}, \end{align*} $$
for
![]() $N \ll T^{3/2+\varepsilon }|T'|^{3/2}$
. Take
$N \ll T^{3/2+\varepsilon }|T'|^{3/2}$
. Take
 $$ \begin{align} R = \left\{ \begin{array}{ll} |T'|^{77/180}T^{-7/36}, & \textrm{ if } T^{5/6} \leq |T'|\leq T, \\ |T'|^{25/36}T^{-15/36}, & \textrm{ if } T^{3/5}\leq |T'|\leq T^{5/6}. \end{array} \right. \end{align} $$
$$ \begin{align} R = \left\{ \begin{array}{ll} |T'|^{77/180}T^{-7/36}, & \textrm{ if } T^{5/6} \leq |T'|\leq T, \\ |T'|^{25/36}T^{-15/36}, & \textrm{ if } T^{3/5}\leq |T'|\leq T^{5/6}. \end{array} \right. \end{align} $$
The contribution from those terms to
![]() $L(1/2+it,\pi \times f )$
is bounded by
$L(1/2+it,\pi \times f )$
is bounded by
![]() $T^{3/4+\varepsilon } |T'|^{3/4} R^{-9/14}$
, which is good enough for Theorem 1.1. Hence, we get
$T^{3/4+\varepsilon } |T'|^{3/4} R^{-9/14}$
, which is good enough for Theorem 1.1. Hence, we get
 $$ \begin{align} L(1/2+it,\phi\times f) \ll T^{\varepsilon} \sum_{r\leq R} \frac{1}{r} \sup_{ N \leq \frac{T^{3/2+\varepsilon}|T'|^{3/2}}{r^2}} \frac{|S_r(N)|}{N^{1/2}} + T^{7/8+\varepsilon} |T'|^{19/40} + T^{57/56+\varepsilon} |T'|^{17/56} , \end{align} $$
$$ \begin{align} L(1/2+it,\phi\times f) \ll T^{\varepsilon} \sum_{r\leq R} \frac{1}{r} \sup_{ N \leq \frac{T^{3/2+\varepsilon}|T'|^{3/2}}{r^2}} \frac{|S_r(N)|}{N^{1/2}} + T^{7/8+\varepsilon} |T'|^{19/40} + T^{57/56+\varepsilon} |T'|^{17/56} , \end{align} $$
where
 $$\begin{align*}S_r(N) := \sum_{n\geq1} A(r,n) \lambda_f(n) n^{-it} V\left(\frac{n}{N}\right). \end{align*}$$
$$\begin{align*}S_r(N) := \sum_{n\geq1} A(r,n) \lambda_f(n) n^{-it} V\left(\frac{n}{N}\right). \end{align*}$$
Thus, to prove Theorem 1.1, we only need to prove the following proposition.
Proposition 2.2. Assume
![]() $|T'| \geq T^{3/5}$
. For
$|T'| \geq T^{3/5}$
. For
![]() $r\leq R$
and
$r\leq R$
and
![]() $ N \leq \frac {T^{3/2+\varepsilon }|T'|^{3/2}}{r^2}$
, we have
$ N \leq \frac {T^{3/2+\varepsilon }|T'|^{3/2}}{r^2}$
, we have
2.3 Summation formulas
We first recall the Poisson summation formula over an arithmetic progression.
Lemma 2.3. Let
![]() $\beta \in \mathbb {Z}$
and
$\beta \in \mathbb {Z}$
and
![]() $c\in \mathbb {Z}_{\geq 1}$
. For a Schwartz function
$c\in \mathbb {Z}_{\geq 1}$
. For a Schwartz function
![]() $f:\mathbb {R}\rightarrow \mathbb {C}$
, we have
$f:\mathbb {R}\rightarrow \mathbb {C}$
, we have
 $$\begin{align*}\sum_{\substack{n\in\mathbb{Z}\\ n\equiv \beta \bmod{c}}} f(n) = \frac{1}{c} \sum_{n\in\mathbb{Z}} \hat{f}\left(\frac{n}{c}\right) e\left(\frac{n\beta}{c}\right), \end{align*}$$
$$\begin{align*}\sum_{\substack{n\in\mathbb{Z}\\ n\equiv \beta \bmod{c}}} f(n) = \frac{1}{c} \sum_{n\in\mathbb{Z}} \hat{f}\left(\frac{n}{c}\right) e\left(\frac{n\beta}{c}\right), \end{align*}$$
where
![]() $\hat {f}(y)=\int _{\mathbb {R}} f(x) e(-xy)\mathrm {d} x$
is the Fourier transform of f.
$\hat {f}(y)=\int _{\mathbb {R}} f(x) e(-xy)\mathrm {d} x$
is the Fourier transform of f.
Proof. See, for example [Reference Iwaniec and Kowalski22, Equation (4.24)].
Now, we turn to the Voronoi summation formula for
![]() $\operatorname {SL}(2,\mathbb {Z})$
. Let f be a weight zero Hecke–Maass cusp form for
$\operatorname {SL}(2,\mathbb {Z})$
. Let f be a weight zero Hecke–Maass cusp form for
![]() $\operatorname {SL}(2,\mathbb {Z})$
with spectral parameter
$\operatorname {SL}(2,\mathbb {Z})$
with spectral parameter
![]() $t_f$
. Let
$t_f$
. Let
![]() $\epsilon _f=\pm 1$
depending on if f is even or odd. Let
$\epsilon _f=\pm 1$
depending on if f is even or odd. Let
![]() $g(x),\ \psi (x)$
be smooth functions with compact support on the positive reals. Let
$g(x),\ \psi (x)$
be smooth functions with compact support on the positive reals. Let
![]() $q\in \mathbb {Z}_{\geq 1}$
and
$q\in \mathbb {Z}_{\geq 1}$
and
![]() $a\in \mathbb {Z}$
with
$a\in \mathbb {Z}$
with
![]() $(q,a)=1$
. Define
$(q,a)=1$
. Define
![]() $\bar {a}$
as the inverse of a modulo q, that is,
$\bar {a}$
as the inverse of a modulo q, that is,
![]() $a\bar {a}\equiv 1 \pmod {q}$
.
$a\bar {a}\equiv 1 \pmod {q}$
.
Lemma 2.4. With the notation as above. Then we have
 $$ \begin{align} \sum_{n\geq1} \lambda_f(n) e\left(\frac{an}{q}\right) g(n) = q \sum_{\pm} \sum_{n\geq1} \frac{ \lambda_{f}(n) }{n} e\left(\mp\frac{\bar{a} n}{q}\right) G^{\pm} \left(\frac{n}{q^2} \right), \end{align} $$
$$ \begin{align} \sum_{n\geq1} \lambda_f(n) e\left(\frac{an}{q}\right) g(n) = q \sum_{\pm} \sum_{n\geq1} \frac{ \lambda_{f}(n) }{n} e\left(\mp\frac{\bar{a} n}{q}\right) G^{\pm} \left(\frac{n}{q^2} \right), \end{align} $$
where
 $$ \begin{align} G^{\pm}(y) & = \frac{\epsilon_f^{(1\mp 1)/2}}{4\pi^2 i} \int_{(\sigma)} (\pi^2 y)^{-s} \left( \frac{\Gamma(\frac{1+s+it_f}{2})\Gamma(\frac{1+s-it_f}{2})} {\Gamma(\frac{-s+it_f}{2})\Gamma(\frac{-s-it_f}{2})} \mp \frac{\Gamma(\frac{2+s+it_f}{2})\Gamma(\frac{2+s-it_f}{2})} {\Gamma(\frac{1-s+it_f}{2})\Gamma(\frac{1-s-it_f}{2})} \right) \tilde{g}(-s) \mathrm{d} s \nonumber\\ & = \epsilon_f^{(1\mp 1)/2} y \int_{0}^{\infty} g(x) J^{\pm}_{f}\left( 4\pi\sqrt{yx} \right) \mathrm{d} x, \end{align} $$
$$ \begin{align} G^{\pm}(y) & = \frac{\epsilon_f^{(1\mp 1)/2}}{4\pi^2 i} \int_{(\sigma)} (\pi^2 y)^{-s} \left( \frac{\Gamma(\frac{1+s+it_f}{2})\Gamma(\frac{1+s-it_f}{2})} {\Gamma(\frac{-s+it_f}{2})\Gamma(\frac{-s-it_f}{2})} \mp \frac{\Gamma(\frac{2+s+it_f}{2})\Gamma(\frac{2+s-it_f}{2})} {\Gamma(\frac{1-s+it_f}{2})\Gamma(\frac{1-s-it_f}{2})} \right) \tilde{g}(-s) \mathrm{d} s \nonumber\\ & = \epsilon_f^{(1\mp 1)/2} y \int_{0}^{\infty} g(x) J^{\pm}_{f}\left( 4\pi\sqrt{yx} \right) \mathrm{d} x, \end{align} $$
with
![]() $\sigma>\theta _2-1$
and
$\sigma>\theta _2-1$
and
![]() $\tilde {g}(s) = \int _{0}^{\infty } g(x) x^{s-1} \mathrm {d} x$
the Mellin transform of g, and
$\tilde {g}(s) = \int _{0}^{\infty } g(x) x^{s-1} \mathrm {d} x$
the Mellin transform of g, and
Proof. See [Reference Miller and Schmid37, Equations (1.12) & (1.15)] and [Reference Kowalski, Michel and VanderKam27, Appendix A].
We also recall the Voronoi summation formula for
![]() $\operatorname {SL}(3,\mathbb {Z})$
. Let
$\operatorname {SL}(3,\mathbb {Z})$
. Let
![]() $\psi $
be a smooth compactly supported function on
$\psi $
be a smooth compactly supported function on
![]() $(0,\infty )$
, and let
$(0,\infty )$
, and let
![]() $\tilde {\psi }$
be the Mellin transform of
$\tilde {\psi }$
be the Mellin transform of
![]() $\psi $
. For
$\psi $
. For
![]() $\sigma>5/14$
, we define
$\sigma>5/14$
, we define
 $$ \begin{align} \Psi^{\pm}(z) := z \frac{1}{2\pi i} \int_{(\sigma)} (\pi^3z)^{-s} \gamma^{\pm}(s) \tilde{\psi}(1-s)\mathrm{d} s , \end{align} $$
$$ \begin{align} \Psi^{\pm}(z) := z \frac{1}{2\pi i} \int_{(\sigma)} (\pi^3z)^{-s} \gamma^{\pm}(s) \tilde{\psi}(1-s)\mathrm{d} s , \end{align} $$
with
 $$ \begin{align} \gamma^{\pm}(s) := \prod_{j=1}^{3} \frac{\Gamma\left(\frac{s+\alpha_j}{2}\right)} {\Gamma\left(\frac{1-s-\alpha_j}{2}\right)} \pm \frac{1}{i} \prod_{j=1}^{3} \frac{\Gamma\left(\frac{1+s+\alpha_j}{2}\right)} {\Gamma\left(\frac{2-s-\alpha_j}{2}\right)}, \end{align} $$
$$ \begin{align} \gamma^{\pm}(s) := \prod_{j=1}^{3} \frac{\Gamma\left(\frac{s+\alpha_j}{2}\right)} {\Gamma\left(\frac{1-s-\alpha_j}{2}\right)} \pm \frac{1}{i} \prod_{j=1}^{3} \frac{\Gamma\left(\frac{1+s+\alpha_j}{2}\right)} {\Gamma\left(\frac{2-s-\alpha_j}{2}\right)}, \end{align} $$
where
![]() $\alpha _j$
are the Langlands parameters of
$\alpha _j$
are the Langlands parameters of
![]() $\phi $
as above. Note that changing
$\phi $
as above. Note that changing
![]() $\psi (y)$
to
$\psi (y)$
to
![]() $\psi (y/N)$
for a positive real number N has the effect of changing
$\psi (y/N)$
for a positive real number N has the effect of changing
![]() $\Psi ^{\pm }(z)$
to
$\Psi ^{\pm }(z)$
to
![]() $\Psi ^{\pm }(zN)$
. The Voronoi formula on
$\Psi ^{\pm }(zN)$
. The Voronoi formula on
![]() $\operatorname {GL}(3)$
was first proved by Miller–Schmid [Reference Miller and Schmid37]. The present version is due to Goldfeld–Li [Reference Goldfeld and Li13] with slightly renormalized variables (see Blomer [Reference Blomer4, Lemma 3]).
$\operatorname {GL}(3)$
was first proved by Miller–Schmid [Reference Miller and Schmid37]. The present version is due to Goldfeld–Li [Reference Goldfeld and Li13] with slightly renormalized variables (see Blomer [Reference Blomer4, Lemma 3]).
Lemma 2.5. Let
![]() $c,d,\bar {d}\in \mathbb Z$
with
$c,d,\bar {d}\in \mathbb Z$
with
![]() $c\neq 0$
,
$c\neq 0$
,
![]() $(c,d)=1$
, and
$(c,d)=1$
, and
![]() $d\bar {d}\equiv 1\pmod {c}$
. Then we have
$d\bar {d}\equiv 1\pmod {c}$
. Then we have
 $$ \begin{align*} \begin{aligned} \sum_{n=1}^{\infty} A(r,n)e\left(\frac{n\bar{d}}{c}\right)\psi(n) = \frac{c\pi^{3/2}}{2} \sum_{\pm} \sum_{n_1|cr} \sum_{n_2=1}^{\infty} \frac{A(n_2,n_1)}{n_1n_2} S\left(rd,\pm n_2;\frac{rc}{n_1}\right) \Psi^{\pm}\left(\frac{n_1^2n_2}{c^3r}\right), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \sum_{n=1}^{\infty} A(r,n)e\left(\frac{n\bar{d}}{c}\right)\psi(n) = \frac{c\pi^{3/2}}{2} \sum_{\pm} \sum_{n_1|cr} \sum_{n_2=1}^{\infty} \frac{A(n_2,n_1)}{n_1n_2} S\left(rd,\pm n_2;\frac{rc}{n_1}\right) \Psi^{\pm}\left(\frac{n_1^2n_2}{c^3r}\right), \end{aligned} \end{align*} $$
where
![]() $S(a,b;c) := \mathop {{\sum }^*}_{d(c)} e\left (\frac {ad+b\bar {d}}{c}\right )$
is the classical Kloosterman sum.
$S(a,b;c) := \mathop {{\sum }^*}_{d(c)} e\left (\frac {ad+b\bar {d}}{c}\right )$
is the classical Kloosterman sum.
2.4 The delta method
There are several oscillatory factors contributing to the convolution sums. Our method is based on separating these oscillations using the delta/circle method. In the present situation, we will use a version of the delta method of Duke, Friedlander, and Iwaniec. More specifically, we will use the expansion (20.157) given in [Reference Iwaniec and Kowalski22, Section 20.5]. Let
![]() $\delta :\mathbb {Z}\rightarrow \{0,1\}$
be defined by
$\delta :\mathbb {Z}\rightarrow \{0,1\}$
be defined by
 $$ \begin{align*}\delta(n)=\begin{cases} 1&\text{if}\;\;n=0;\\ 0&\text{otherwise}.\end{cases} \end{align*} $$
$$ \begin{align*}\delta(n)=\begin{cases} 1&\text{if}\;\;n=0;\\ 0&\text{otherwise}.\end{cases} \end{align*} $$
We seek a Fourier expansion which matches with
![]() $\delta (n)$
.
$\delta (n)$
.
Lemma 2.6. Let Q be a large positive number. Then we have
 $$ \begin{align} \delta(n)=\frac{1}{Q}\sum_{1\leq q\leq Q} \;\frac{1}{q}\; \sideset{}{^{\star}}\sum_{a\bmod{q}}e\left(\frac{na}{q}\right) \int_{\mathbb{R}} g(q,x) e\left(\frac{nx}{qQ}\right)\mathrm{d}x, \end{align} $$
$$ \begin{align} \delta(n)=\frac{1}{Q}\sum_{1\leq q\leq Q} \;\frac{1}{q}\; \sideset{}{^{\star}}\sum_{a\bmod{q}}e\left(\frac{na}{q}\right) \int_{\mathbb{R}} g(q,x) e\left(\frac{nx}{qQ}\right)\mathrm{d}x, \end{align} $$
where
![]() $g(q,x)$
is a weight function that satisfies that
$g(q,x)$
is a weight function that satisfies that
 $$ \begin{align} g(q,x)=1+O\left(\frac{Q}{q}\left(\frac{q}{Q}+|x|\right)^A\right), \quad g(q,x)\ll |x|^{-A}, \quad \textrm{for any } A>1, \end{align} $$
$$ \begin{align} g(q,x)=1+O\left(\frac{Q}{q}\left(\frac{q}{Q}+|x|\right)^A\right), \quad g(q,x)\ll |x|^{-A}, \quad \textrm{for any } A>1, \end{align} $$
and
Here, the
![]() $\star $
on the sum indicates that the sum over a is restricted by the condition
$\star $
on the sum indicates that the sum over a is restricted by the condition
![]() $(a,q)=1$
.
$(a,q)=1$
.
Proof. See [Reference Huang18, Lemma 15].
2.5 Weight functions
Let
![]() $\mathcal {F}$
be an index set and
$\mathcal {F}$
be an index set and
![]() $X=X_T:\mathcal {F}\rightarrow \mathbb {R}_{\geq 1}$
be a function of
$X=X_T:\mathcal {F}\rightarrow \mathbb {R}_{\geq 1}$
be a function of
![]() $T\in \mathcal {F}$
. A family of
$T\in \mathcal {F}$
. A family of
![]() $\{w_T\}_{T\in \mathcal {F}}$
of smooth functions supported on a product of dyadic intervals in
$\{w_T\}_{T\in \mathcal {F}}$
of smooth functions supported on a product of dyadic intervals in
![]() $\mathbb {R}_{>0}^d$
is called X-inert if for each
$\mathbb {R}_{>0}^d$
is called X-inert if for each
![]() $j=(j_1,\ldots ,j_d) \in \mathbb {Z}_{\geq 0}^d$
we have
$j=(j_1,\ldots ,j_d) \in \mathbb {Z}_{\geq 0}^d$
we have
 $$\begin{align*}\sup_{T\in\mathcal{F}} \sup_{(x_1,\ldots,x_d) \in \mathbb{R}_{>0}^d} X_T^{-j_1-\cdots -j_d} \left| x_1^{j_1} \cdots x_d^{j_d} w_T^{(j_1,\ldots,j_d)} (x_1,\ldots,x_d) \right| \ll_{j_1,\ldots,j_d} 1. \end{align*}$$
$$\begin{align*}\sup_{T\in\mathcal{F}} \sup_{(x_1,\ldots,x_d) \in \mathbb{R}_{>0}^d} X_T^{-j_1-\cdots -j_d} \left| x_1^{j_1} \cdots x_d^{j_d} w_T^{(j_1,\ldots,j_d)} (x_1,\ldots,x_d) \right| \ll_{j_1,\ldots,j_d} 1. \end{align*}$$
For a
![]() $T^{\varepsilon }$
-inert function V, we may separate variables in
$T^{\varepsilon }$
-inert function V, we may separate variables in
![]() $V(x_1, \ldots , x_d)$
by first inserting a redundant function
$V(x_1, \ldots , x_d)$
by first inserting a redundant function
![]() $V (x_1) \cdots V (x_d)$
that is 1 on the support of V and then applying the Mellin inversion
$V (x_1) \cdots V (x_d)$
that is 1 on the support of V and then applying the Mellin inversion
 $$ \begin{align*} V (x_1, \ldots , x_d) &= V (x_1, \ldots , x_d)V (x_1) \cdots V (x_d) \\& = \frac{1}{(2\pi i)^d} \int_{(0)}\cdots \int_{(0)} \tilde{V}(s_1,\ldots,s_d) (V (x_1) \cdots V (x_d) x_1^{-s_1} \cdots x_n^{-s_d} ) \mathrm{d} s_1 \cdots \mathrm{d} s_d, \end{align*} $$
$$ \begin{align*} V (x_1, \ldots , x_d) &= V (x_1, \ldots , x_d)V (x_1) \cdots V (x_d) \\& = \frac{1}{(2\pi i)^d} \int_{(0)}\cdots \int_{(0)} \tilde{V}(s_1,\ldots,s_d) (V (x_1) \cdots V (x_d) x_1^{-s_1} \cdots x_n^{-s_d} ) \mathrm{d} s_1 \cdots \mathrm{d} s_d, \end{align*} $$
where
![]() $\tilde {V}(s_1,\ldots ,s_d)=\int _{0}^{\infty }\cdots \int _{0}^{\infty } V(x_1, \ldots , x_d) x_1^{s_1-1} \cdots x_d^{s_d-1} \mathrm {d} x_1 \cdots \mathrm {d} x_d$
is the Mellin transform of V. Here, we can truncate the vertical integrals at height
$\tilde {V}(s_1,\ldots ,s_d)=\int _{0}^{\infty }\cdots \int _{0}^{\infty } V(x_1, \ldots , x_d) x_1^{s_1-1} \cdots x_d^{s_d-1} \mathrm {d} x_1 \cdots \mathrm {d} x_d$
is the Mellin transform of V. Here, we can truncate the vertical integrals at height
![]() $|\operatorname {Im} s_j| \ll T^{2\varepsilon }$
at the cost of a negligible error
$|\operatorname {Im} s_j| \ll T^{2\varepsilon }$
at the cost of a negligible error
![]() $O_A(T^{-A})$
. We will often separate variables in this way without explicit mention.
$O_A(T^{-A})$
. We will often separate variables in this way without explicit mention.
2.6 Oscillatory integrals
We will use the following integration by parts and stationary phase lemmas several times.
Lemma 2.7. Let
![]() $Y\geq 1$
. Let
$Y\geq 1$
. Let
![]() $X,\; V,\; R,\; Q>0$
, and suppose that
$X,\; V,\; R,\; Q>0$
, and suppose that
![]() $w=w_T$
is a smooth function with
$w=w_T$
is a smooth function with
![]() $\operatorname {supp} w \subseteq [\alpha ,\beta ]$
satisfying
$\operatorname {supp} w \subseteq [\alpha ,\beta ]$
satisfying
![]() $w^{(j)}(\xi ) \ll _j X V^{-j}$
for all
$w^{(j)}(\xi ) \ll _j X V^{-j}$
for all
![]() $j\geq 0$
. Suppose that on the support of w,
$j\geq 0$
. Suppose that on the support of w,
![]() $h=h_T$
is smooth and satisfies that
$h=h_T$
is smooth and satisfies that
![]() $h'(\xi )\gg R$
and
$h'(\xi )\gg R$
and
![]() $ h^{(j)}(\xi ) \ll Y Q^{-j}$
, for all
$ h^{(j)}(\xi ) \ll Y Q^{-j}$
, for all
![]() $j\geq 2.$
Then, for arbitrarily large A, we have
$j\geq 2.$
Then, for arbitrarily large A, we have
 $$\begin{align*}I = \int_{\mathbb{R}} w(\xi) e(h(\xi)) \mathrm{d} \xi \ll_A (\beta-\alpha) X \left[ \left(\frac{QR}{\sqrt{Y}}\right)^{-A} + (RV)^{-A} \right]. \end{align*}$$
$$\begin{align*}I = \int_{\mathbb{R}} w(\xi) e(h(\xi)) \mathrm{d} \xi \ll_A (\beta-\alpha) X \left[ \left(\frac{QR}{\sqrt{Y}}\right)^{-A} + (RV)^{-A} \right]. \end{align*}$$
Proof. See [Reference Blomer, Khan and Young7, Lemma 8.1].
Lemma 2.8. Suppose
![]() $w_T$
is X-inert in
$w_T$
is X-inert in
![]() $t_1,\ldots ,t_d$
, supported on
$t_1,\ldots ,t_d$
, supported on
![]() $t_i\asymp X_i$
for
$t_i\asymp X_i$
for
![]() $i=1,2,\ldots ,d$
. Suppose that on the support of
$i=1,2,\ldots ,d$
. Suppose that on the support of
![]() $w_T$
,
$w_T$
,
![]() $h=h_T$
satisfies that
$h=h_T$
satisfies that
 $$\begin{align*}\frac{\partial^{a_1+a_2+\cdots +a_d}}{\partial t_1^{a_1}\cdots \partial t_d^{a_d}} h(t_1,t_2,\ldots,t_d) \ll_{a_1,\ldots,a_d} \frac{Y}{X_1^{a_1} X_2^{a_2}\cdots X_d^{a_d}}, \end{align*}$$
$$\begin{align*}\frac{\partial^{a_1+a_2+\cdots +a_d}}{\partial t_1^{a_1}\cdots \partial t_d^{a_d}} h(t_1,t_2,\ldots,t_d) \ll_{a_1,\ldots,a_d} \frac{Y}{X_1^{a_1} X_2^{a_2}\cdots X_d^{a_d}}, \end{align*}$$
for all
![]() $a_1,\ldots ,a_d\in \mathbb {Z}_{\geq 0}$
. Let
$a_1,\ldots ,a_d\in \mathbb {Z}_{\geq 0}$
. Let
Suppose
![]() $\frac {\partial ^{2}}{\partial t_1^{2}} h(t_1,t_2,\ldots ,t_d) \gg \frac {Y}{X_1^2}$
for all
$\frac {\partial ^{2}}{\partial t_1^{2}} h(t_1,t_2,\ldots ,t_d) \gg \frac {Y}{X_1^2}$
for all
![]() $(t_1,t_2,\ldots ,t_d)\in \operatorname {supp} w_T$
, and there exists
$(t_1,t_2,\ldots ,t_d)\in \operatorname {supp} w_T$
, and there exists
![]() $t_0 \in \mathbb {R}$
, such that
$t_0 \in \mathbb {R}$
, such that
![]() $ \frac {\partial }{\partial t_1} h(t_0,t_2,\ldots ,t_d)=0$
. Suppose that
$ \frac {\partial }{\partial t_1} h(t_0,t_2,\ldots ,t_d)=0$
. Suppose that
![]() $Y/X^2 \geq R \geq 1$
. Then
$Y/X^2 \geq R \geq 1$
. Then
for some X-inert family of functions
![]() $W_T$
and any
$W_T$
and any
![]() $A>0$
.
$A>0$
.
Proof. See [Reference Blomer, Khan and Young7, Section 8] and [Reference Kıral, Petrow and Young26, Section 3].
In the applications of Lemma 2.8, we will explicitly give estimates of the derivatives for the first variable. For other derivatives, we will also check all those conditions but may not write them down explicitly.
2.7 Stirling’s formula
For fixed
![]() $\sigma \in \mathbb {R}$
, real
$\sigma \in \mathbb {R}$
, real
![]() $|t|\geq 10$
, and any
$|t|\geq 10$
, and any
![]() $J>0$
, we have Stirling’s formula
$J>0$
, we have Stirling’s formula
 $$ \begin{align*} \Gamma(\sigma+it) = e^{-\frac{\pi}{2}|t|} |t|^{\sigma-\frac{1}{2}} \exp\left( it\log\frac{|t|}{e} \right) \left( g_{\sigma,J}(t) + O_{\sigma,J}(|t|^{-J}) \right), \end{align*} $$
$$ \begin{align*} \Gamma(\sigma+it) = e^{-\frac{\pi}{2}|t|} |t|^{\sigma-\frac{1}{2}} \exp\left( it\log\frac{|t|}{e} \right) \left( g_{\sigma,J}(t) + O_{\sigma,J}(|t|^{-J}) \right), \end{align*} $$
where
for all fixed
![]() $j\in \mathbb {N}_0$
. Similarly, we have
$j\in \mathbb {N}_0$
. Similarly, we have
 $$ \begin{align*} \frac{1}{\Gamma(\sigma+it)} = e^{\frac{\pi}{2}|t|} |t|^{-\sigma+\frac{1}{2}} \exp\left( -it\log\frac{|t|}{e} \right) \left( h_{\sigma,J}(t) + O_{\sigma,J}(|t|^{-J}) \right), \end{align*} $$
$$ \begin{align*} \frac{1}{\Gamma(\sigma+it)} = e^{\frac{\pi}{2}|t|} |t|^{-\sigma+\frac{1}{2}} \exp\left( -it\log\frac{|t|}{e} \right) \left( h_{\sigma,J}(t) + O_{\sigma,J}(|t|^{-J}) \right), \end{align*} $$
where
for all fixed
![]() $j\in \mathbb {N}_0$
. Hence
$j\in \mathbb {N}_0$
. Hence
 $$ \begin{align} \frac{\Gamma(\sigma+it)}{\Gamma(\sigma-it)} = \exp\left( 2it\log\frac{|t|}{e} \right) \left( w_{\sigma,J}(t) + O_{\sigma,J}(|t|^{-J}) \right), \end{align} $$
$$ \begin{align} \frac{\Gamma(\sigma+it)}{\Gamma(\sigma-it)} = \exp\left( 2it\log\frac{|t|}{e} \right) \left( w_{\sigma,J}(t) + O_{\sigma,J}(|t|^{-J}) \right), \end{align} $$
where
for all fixed
![]() $j\in \mathbb {N}_0$
.
$j\in \mathbb {N}_0$
.
2.8 Bessel functions
We need the following asymptotic formula for Bessel functions when
![]() $x\gg T^{\varepsilon } |\tau |$
. For
$x\gg T^{\varepsilon } |\tau |$
. For
![]() $\tau \in \mathbb {R}$
,
$\tau \in \mathbb {R}$
,
![]() $|\tau |>1$
and
$|\tau |>1$
and
![]() $x>0$
, we have [Reference Erdélyi, Magnus, Oberhettinger and Tricomi11, Equation 7.13.2 (17)]
$x>0$
, we have [Reference Erdélyi, Magnus, Oberhettinger and Tricomi11, Equation 7.13.2 (17)]
 $$ \begin{align} \frac{J_{2i\tau}(2x)}{\cosh(\pi \tau)} = \sum_{\pm} e^{\pm 2i \omega(x,\tau)} \frac{g_A^{\pm}(x,\tau)}{x^{1/2}+|\tau|^{1/2}} + O(x^{-A}), \end{align} $$
$$ \begin{align} \frac{J_{2i\tau}(2x)}{\cosh(\pi \tau)} = \sum_{\pm} e^{\pm 2i \omega(x,\tau)} \frac{g_A^{\pm}(x,\tau)}{x^{1/2}+|\tau|^{1/2}} + O(x^{-A}), \end{align} $$
where
![]() $g_A^{\pm }(x,\tau )$
is an
$g_A^{\pm }(x,\tau )$
is an
![]() $1$
-inert function and
$1$
-inert function and
For
![]() $x\geq T^{\varepsilon } |\tau |$
, we have [Reference Erdélyi, Magnus, Oberhettinger and Tricomi11, Equation 7.13.2 (18)]
$x\geq T^{\varepsilon } |\tau |$
, we have [Reference Erdélyi, Magnus, Oberhettinger and Tricomi11, Equation 7.13.2 (18)]
for T large enough.
3 Applying the delta method
By the delta method (Lemma 2.6), we have
 $$ \begin{align*} S_r(N) & = \sum_{n\geq1} A(r,n) V\left(\frac{n}{N}\right) \sum_{\substack{m\geq1}} \lambda_f(m) m^{-it} W\left(\frac{m}{N}\right) \delta\left( m-n \right) \\ & = \sum_{n\geq1} A(r,n) V\left(\frac{n}{N}\right) \sum_{\substack{m\geq1}} \lambda_f(m) m^{-it} W\left(\frac{m}{N}\right) \\ & \hskip 50pt \cdot \frac{1}{Q}\sum_{1\leq q\leq Q} \;\frac{1}{q}\; \sideset{}{^{\star}}\sum_{a\bmod{q}}e\left(\frac{(m-n)a}{q}\right) \int_{\mathbb{R}}g(q,x) e\left(\frac{(m-n)x}{qQ}\right)\mathrm{d}x, \end{align*} $$
$$ \begin{align*} S_r(N) & = \sum_{n\geq1} A(r,n) V\left(\frac{n}{N}\right) \sum_{\substack{m\geq1}} \lambda_f(m) m^{-it} W\left(\frac{m}{N}\right) \delta\left( m-n \right) \\ & = \sum_{n\geq1} A(r,n) V\left(\frac{n}{N}\right) \sum_{\substack{m\geq1}} \lambda_f(m) m^{-it} W\left(\frac{m}{N}\right) \\ & \hskip 50pt \cdot \frac{1}{Q}\sum_{1\leq q\leq Q} \;\frac{1}{q}\; \sideset{}{^{\star}}\sum_{a\bmod{q}}e\left(\frac{(m-n)a}{q}\right) \int_{\mathbb{R}}g(q,x) e\left(\frac{(m-n)x}{qQ}\right)\mathrm{d}x, \end{align*} $$
where W is a fixed smooth function, such that
![]() $\operatorname {supp} W \subset \mathbb {R}^+$
and
$\operatorname {supp} W \subset \mathbb {R}^+$
and
![]() $W(u)=1$
if
$W(u)=1$
if
![]() $u\in \operatorname {supp} V$
, and
$u\in \operatorname {supp} V$
, and
![]() $W^{(j)}(u)\ll _j 1$
for any
$W^{(j)}(u)\ll _j 1$
for any
![]() $j\geq 0$
. Inserting a smooth partition of unity for the x-integral and a dyadic partition for the q-sum, we get
$j\geq 0$
. Inserting a smooth partition of unity for the x-integral and a dyadic partition for the q-sum, we get
where
![]() $B=B(A)>0$
is a large constant depending on A and
$B=B(A)>0$
is a large constant depending on A and
 $$ \begin{align*} S_{r}^{\pm}(N,X,P) & = \frac{1}{Q}\sum_{\substack{q\sim P}} \int_{\mathbb{R}} V\left(\frac{\pm x}{X}\right) \;\frac{1}{q}\; \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} \sum_{n\geq1} A(r,n) e\left(\frac{-an}{q}\right) e\left(\frac{-nx}{qQ}\right) V\left(\frac{n}{N}\right) \\ & \hskip 90pt \cdot \sum_{\substack{m\geq1}} \lambda_f(m) e\left(\frac{m a}{q}\right) e\left(\frac{m x}{qQ}\right) m^{-it} W\left(\frac{m}{N}\right) \mathrm{d}x. \end{align*} $$
$$ \begin{align*} S_{r}^{\pm}(N,X,P) & = \frac{1}{Q}\sum_{\substack{q\sim P}} \int_{\mathbb{R}} V\left(\frac{\pm x}{X}\right) \;\frac{1}{q}\; \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} \sum_{n\geq1} A(r,n) e\left(\frac{-an}{q}\right) e\left(\frac{-nx}{qQ}\right) V\left(\frac{n}{N}\right) \\ & \hskip 90pt \cdot \sum_{\substack{m\geq1}} \lambda_f(m) e\left(\frac{m a}{q}\right) e\left(\frac{m x}{qQ}\right) m^{-it} W\left(\frac{m}{N}\right) \mathrm{d}x. \end{align*} $$
4 Applying Voronoi
We first apply the Voronoi summation formula to the sum over n (see Lemma 2.5), getting
 $$ \begin{align*} \sum_{n\geq1} A(r,n) e\left(\frac{-an}{q}\right) & e\left(\frac{-nx}{qQ}\right) V\left(\frac{n}{N}\right) \\ & = \frac{q\pi^{3/2}}{2} \sum_{\pm} \sum_{n_1|qr} \sum_{n_2=1}^{\infty} \frac{A(n_2,n_1)}{n_1n_2} S\left(-r\bar{a},\pm n_2;\frac{rq}{n_1}\right) \Psi_x^{\pm}\left(\frac{n_1^2n_2}{q^3r}\right), \end{align*} $$
$$ \begin{align*} \sum_{n\geq1} A(r,n) e\left(\frac{-an}{q}\right) & e\left(\frac{-nx}{qQ}\right) V\left(\frac{n}{N}\right) \\ & = \frac{q\pi^{3/2}}{2} \sum_{\pm} \sum_{n_1|qr} \sum_{n_2=1}^{\infty} \frac{A(n_2,n_1)}{n_1n_2} S\left(-r\bar{a},\pm n_2;\frac{rq}{n_1}\right) \Psi_x^{\pm}\left(\frac{n_1^2n_2}{q^3r}\right), \end{align*} $$
where
![]() $\psi _x(u)=e\left (-\frac {ux}{qQ}\right ) V\left (\frac {u}{N}\right )$
and
$\psi _x(u)=e\left (-\frac {ux}{qQ}\right ) V\left (\frac {u}{N}\right )$
and
![]() $\Psi _x^{\pm }$
defined as in (2.9) with
$\Psi _x^{\pm }$
defined as in (2.9) with
![]() $\psi $
replaced by
$\psi $
replaced by
![]() $\psi _x$
.
$\psi _x$
.
Lemma 4.1. We have
-
(i) if
 $zN\gg T^{\varepsilon }$
, then
$zN\gg T^{\varepsilon }$
, then
 $\Psi ^{\pm }_x(z) \ll z^{-6} T^{-A}$
is negligibly small unless
$\Psi ^{\pm }_x(z) \ll z^{-6} T^{-A}$
is negligibly small unless
 $\operatorname {sgn}(x) = \pm $
and
$\operatorname {sgn}(x) = \pm $
and
 $\pm \frac {Nx}{qQ} \asymp (zN)^{1/3}$
, in which case, we have (4.1)where w is a certain compactly supported
$\pm \frac {Nx}{qQ} \asymp (zN)^{1/3}$
, in which case, we have (4.1)where w is a certain compactly supported $$ \begin{align} \Psi_x^{\pm}(z) = \left(\pm \frac{Nx}{qQ}\right)^{3/2} e\left(\pm 2 \frac{(zN)^{1/2}}{(\pm \frac{Nx}{qQ})^{1/2}}\right) w\left(\frac{ zN }{(\pm \frac{Nx}{qQ})^{3}}\right) + O(T^{-A}) \ll (zN)^{1/2}, \end{align} $$
$$ \begin{align} \Psi_x^{\pm}(z) = \left(\pm \frac{Nx}{qQ}\right)^{3/2} e\left(\pm 2 \frac{(zN)^{1/2}}{(\pm \frac{Nx}{qQ})^{1/2}}\right) w\left(\frac{ zN }{(\pm \frac{Nx}{qQ})^{3}}\right) + O(T^{-A}) \ll (zN)^{1/2}, \end{align} $$
 $1$
-inert function depending on A;
$1$
-inert function depending on A;
-
(ii) if
 $zN\ll T^{\varepsilon }$
and
$zN\ll T^{\varepsilon }$
and
 $\frac {Nx}{qQ}\gg T^{\varepsilon }$
, then
$\frac {Nx}{qQ}\gg T^{\varepsilon }$
, then
 $\Psi _x^{\pm }(z) \ll _A T^{-A}$
for any
$\Psi _x^{\pm }(z) \ll _A T^{-A}$
for any
 $A>0$
;
$A>0$
; -
(iii) if
 $zN\ll T^{\varepsilon }$
and
$zN\ll T^{\varepsilon }$
and
 $\frac {Nx}{qQ}\ll T^{\varepsilon }$
, then
$\frac {Nx}{qQ}\ll T^{\varepsilon }$
, then
 $\Psi _x^{\pm }(z) \ll T^{\varepsilon }$
.
$\Psi _x^{\pm }(z) \ll T^{\varepsilon }$
.
Proof. See [Reference Huang18, Section 5.3]
4.1 The oscillating cases
If
![]() $\frac {NX}{PQ}\gg T^{\varepsilon }$
, then we have
$\frac {NX}{PQ}\gg T^{\varepsilon }$
, then we have
 $$ \begin{align*} S_{r}^{\pm}(N,X,P) = \frac{1}{Q}&\sum_{\substack{q\sim P}} \int_{\mathbb{R}} V\left(\frac{\pm x}{X}\right) \;\frac{1}{q}\; \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} \frac{q\pi^{3/2}}{2} \sum_{n_1|qr} \sum_{n_2=1}^{\infty} \frac{A(n_2,n_1)}{n_1n_2} S\left(-r\bar{a},\pm n_2;\frac{rq}{n_1}\right) \\ & \cdot \left(\pm \frac{Nx}{qQ}\right)^{3/2} e\left(\pm 2 \frac{( n_1^2n_2 Q)^{1/2}}{r^{1/2} q(\pm x)^{1/2}}\right) w\left(\frac{n_1^2n_2 Q^3}{r N^2 (\pm x )^{3}}\right) \\ & \cdot \sum_{\substack{m\geq1}} \lambda_f(m) e\left(\frac{m a}{q}\right) e\left(\frac{m x}{qQ}\right) m^{-it} W\left(\frac{m}{N}\right) \mathrm{d}x + O(T^{-A}). \end{align*} $$
$$ \begin{align*} S_{r}^{\pm}(N,X,P) = \frac{1}{Q}&\sum_{\substack{q\sim P}} \int_{\mathbb{R}} V\left(\frac{\pm x}{X}\right) \;\frac{1}{q}\; \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} \frac{q\pi^{3/2}}{2} \sum_{n_1|qr} \sum_{n_2=1}^{\infty} \frac{A(n_2,n_1)}{n_1n_2} S\left(-r\bar{a},\pm n_2;\frac{rq}{n_1}\right) \\ & \cdot \left(\pm \frac{Nx}{qQ}\right)^{3/2} e\left(\pm 2 \frac{( n_1^2n_2 Q)^{1/2}}{r^{1/2} q(\pm x)^{1/2}}\right) w\left(\frac{n_1^2n_2 Q^3}{r N^2 (\pm x )^{3}}\right) \\ & \cdot \sum_{\substack{m\geq1}} \lambda_f(m) e\left(\frac{m a}{q}\right) e\left(\frac{m x}{qQ}\right) m^{-it} W\left(\frac{m}{N}\right) \mathrm{d}x + O(T^{-A}). \end{align*} $$
We first deal with the x-integral. Making a change of variable
![]() $x = \pm X \xi $
, we get
$x = \pm X \xi $
, we get
 $$ \begin{align*} &S_{r}^{\pm}(N,X,P) = X \frac{1}{Q}\sum_{\substack{q\sim P}} \;\frac{1}{q}\; \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} \frac{q\pi^{3/2}}{2} \sum_{n_1|qr} \sum_{n_2=1}^{\infty} \frac{A(n_2,n_1)}{n_1n_2} S\left(-r\bar{a},\pm n_2;\frac{rq}{n_1}\right) \\&\quad \cdot \left(\frac{NX}{qQ}\right)^{3/2} \sum_{\substack{m\geq1}} \lambda_f(m) e\left(\frac{ma}{q}\right) m^{-it} W\left(\frac{m}{N}\right) \\&\quad \cdot \int_{\mathbb{R}} w\left(\frac{n_1^2n_2 Q^3}{r N^2X^{3}\xi^3}\right) V\left(\xi\right) \xi^{3/2} e\left(\frac{\pm m X\xi}{qQ}\right) e\left(\pm 2 \frac{( n_1^2n_2 Q)^{1/2}}{r^{1/2} qX^{1/2} \xi^{1/2}}\right) \mathrm{d}\xi + O(T^{-A}). \end{align*} $$
$$ \begin{align*} &S_{r}^{\pm}(N,X,P) = X \frac{1}{Q}\sum_{\substack{q\sim P}} \;\frac{1}{q}\; \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} \frac{q\pi^{3/2}}{2} \sum_{n_1|qr} \sum_{n_2=1}^{\infty} \frac{A(n_2,n_1)}{n_1n_2} S\left(-r\bar{a},\pm n_2;\frac{rq}{n_1}\right) \\&\quad \cdot \left(\frac{NX}{qQ}\right)^{3/2} \sum_{\substack{m\geq1}} \lambda_f(m) e\left(\frac{ma}{q}\right) m^{-it} W\left(\frac{m}{N}\right) \\&\quad \cdot \int_{\mathbb{R}} w\left(\frac{n_1^2n_2 Q^3}{r N^2X^{3}\xi^3}\right) V\left(\xi\right) \xi^{3/2} e\left(\frac{\pm m X\xi}{qQ}\right) e\left(\pm 2 \frac{( n_1^2n_2 Q)^{1/2}}{r^{1/2} qX^{1/2} \xi^{1/2}}\right) \mathrm{d}\xi + O(T^{-A}). \end{align*} $$
We can remove the weight function
![]() $w\left (\frac {n_1^2n_2 Q^3}{r N^2X^{3}\xi ^3}\right )$
by the Mellin technique as in Section 2.5. Then we have
$w\left (\frac {n_1^2n_2 Q^3}{r N^2X^{3}\xi ^3}\right )$
by the Mellin technique as in Section 2.5. Then we have
 $$ \begin{align*} S_{r}^{\pm}(N,X,P) \ll T^{\varepsilon} \bigg| &\frac{X}{Q}\sum_{\substack{q\sim P}} \; \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} \sum_{n_1|qr} \sum_{n_2=1}^{\infty} \frac{A(n_2,n_1)}{n_1n_2} S\left(-r\bar{a},\pm n_2;\frac{rq}{n_1}\right) V_1\left(\frac{n_1^2n_2 Q^3}{r N^2X^{3}}\right) \\ & \cdot \left(\frac{NX}{qQ}\right)^{3/2} \sum_{\substack{m\geq1}} \lambda_f(m) e\left(\frac{ma}{q}\right) m^{-it} W\left(\frac{m}{N}\right) \\ & \cdot \int_{\mathbb{R}} V_2\left(\xi\right) e\left(\frac{\pm m X\xi}{qQ} \pm 2 \frac{( n_1^2n_2 Q)^{1/2}}{r^{1/2} qX^{1/2} \xi^{1/2}}\right) \mathrm{d}\xi \bigg| + O(T^{-A}), \end{align*} $$
$$ \begin{align*} S_{r}^{\pm}(N,X,P) \ll T^{\varepsilon} \bigg| &\frac{X}{Q}\sum_{\substack{q\sim P}} \; \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} \sum_{n_1|qr} \sum_{n_2=1}^{\infty} \frac{A(n_2,n_1)}{n_1n_2} S\left(-r\bar{a},\pm n_2;\frac{rq}{n_1}\right) V_1\left(\frac{n_1^2n_2 Q^3}{r N^2X^{3}}\right) \\ & \cdot \left(\frac{NX}{qQ}\right)^{3/2} \sum_{\substack{m\geq1}} \lambda_f(m) e\left(\frac{ma}{q}\right) m^{-it} W\left(\frac{m}{N}\right) \\ & \cdot \int_{\mathbb{R}} V_2\left(\xi\right) e\left(\frac{\pm m X\xi}{qQ} \pm 2 \frac{( n_1^2n_2 Q)^{1/2}}{r^{1/2} qX^{1/2} \xi^{1/2}}\right) \mathrm{d}\xi \bigg| + O(T^{-A}), \end{align*} $$
for some
![]() $T^{\varepsilon }$
-inert functions
$T^{\varepsilon }$
-inert functions
![]() $V_1$
and
$V_1$
and
![]() $V_2$
with support in
$V_2$
with support in
![]() $[1,2]$
. We now consider the
$[1,2]$
. We now consider the
![]() $\xi $
-integral above. Let (temporarily)
$\xi $
-integral above. Let (temporarily)
 $$\begin{align*}h(\xi) = \frac{\pm m X\xi}{qQ} \pm 2 \frac{( n_1^2n_2 Q)^{1/2}}{r^{1/2} qX^{1/2} \xi^{1/2}}. \end{align*}$$
$$\begin{align*}h(\xi) = \frac{\pm m X\xi}{qQ} \pm 2 \frac{( n_1^2n_2 Q)^{1/2}}{r^{1/2} qX^{1/2} \xi^{1/2}}. \end{align*}$$
Then
 $$\begin{align*}h'(\xi) = \frac{\pm m X }{qQ} \mp \frac{( n_1^2n_2 Q)^{1/2}}{r^{1/2} qX^{1/2} \xi^{3/2}}, \end{align*}$$
$$\begin{align*}h'(\xi) = \frac{\pm m X }{qQ} \mp \frac{( n_1^2n_2 Q)^{1/2}}{r^{1/2} qX^{1/2} \xi^{3/2}}, \end{align*}$$
and
 $$\begin{align*}h"(\xi) = \pm \frac{3}{2} \frac{( n_1^2n_2 Q)^{1/2}}{r^{1/2} qX^{1/2} \xi^{5/2}} , \quad h^{(j)}(\xi) \asymp_j \frac{NX}{PQ}, \quad j\geq2. \end{align*}$$
$$\begin{align*}h"(\xi) = \pm \frac{3}{2} \frac{( n_1^2n_2 Q)^{1/2}}{r^{1/2} qX^{1/2} \xi^{5/2}} , \quad h^{(j)}(\xi) \asymp_j \frac{NX}{PQ}, \quad j\geq2. \end{align*}$$
The solution of
![]() $h'(\xi )=0$
is
$h'(\xi )=0$
is
![]() $\xi _0 = \frac {( n_1^2n_2)^{1/3} Q}{r^{1/3} m^{2/3}X}$
. Note that
$\xi _0 = \frac {( n_1^2n_2)^{1/3} Q}{r^{1/3} m^{2/3}X}$
. Note that
 $$\begin{align*}h(\xi_0) = \pm 3\frac{m^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \quad \textrm{and} \quad h"(\xi_0) = \pm \frac{3}{2} \frac{mX}{q Q \xi_0 }. \end{align*}$$
$$\begin{align*}h(\xi_0) = \pm 3\frac{m^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \quad \textrm{and} \quad h"(\xi_0) = \pm \frac{3}{2} \frac{mX}{q Q \xi_0 }. \end{align*}$$
Now, by Lemma 2.8 with
 $$\begin{align*}X= T^{\varepsilon}, t_1=\xi, t_2=n_1^2n_2, t_3=m, t_4=q, X_1=1, X_2=\frac{rN^2X^3}{Q^3}, X_3=N, X_4=P, \textrm{ and } Y=\frac{NX}{PQ}, \end{align*}$$
$$\begin{align*}X= T^{\varepsilon}, t_1=\xi, t_2=n_1^2n_2, t_3=m, t_4=q, X_1=1, X_2=\frac{rN^2X^3}{Q^3}, X_3=N, X_4=P, \textrm{ and } Y=\frac{NX}{PQ}, \end{align*}$$
we get
 $$ \begin{align*} &\int_{\mathbb{R}} V_2\left(\xi\right) e \left(\frac{\pm m X\xi}{qQ} \pm 2 \frac{( n_1^2n_2 Q)^{1/2}}{r^{1/2} qX^{1/2} \xi^{1/2}}\right) \mathrm{d}\xi \\&\quad = \left(\frac{NX}{qQ}\right)^{-1/2} V_3\left(\frac{ n_1^2n_2 Q^3}{r N^{2}X^3},\frac{m}{N},\frac{q}{P}\right) e\left(\pm 3\frac{m^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \right) + O_A(T^{-A}), \end{align*} $$
$$ \begin{align*} &\int_{\mathbb{R}} V_2\left(\xi\right) e \left(\frac{\pm m X\xi}{qQ} \pm 2 \frac{( n_1^2n_2 Q)^{1/2}}{r^{1/2} qX^{1/2} \xi^{1/2}}\right) \mathrm{d}\xi \\&\quad = \left(\frac{NX}{qQ}\right)^{-1/2} V_3\left(\frac{ n_1^2n_2 Q^3}{r N^{2}X^3},\frac{m}{N},\frac{q}{P}\right) e\left(\pm 3\frac{m^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \right) + O_A(T^{-A}), \end{align*} $$
where
![]() $V_3$
is a
$V_3$
is a
![]() $T^{\varepsilon }$
-inert function with compact support in
$T^{\varepsilon }$
-inert function with compact support in
![]() $\mathbb {R}_{>0}^3$
. Hence, we obtain
$\mathbb {R}_{>0}^3$
. Hence, we obtain
 $$ \begin{align} S_{r}^{\pm}(N,X,P) & \ll T^{\varepsilon} \bigg| \frac{X}{Q}\sum_{\substack{q\sim P}} \;\frac{1}{q}\; \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} \!\frac{NX}{Q} \sum_{n_1|qr} \sum_{\substack{n_2=1 \\ n_1^2n_2 \asymp \frac{r N^{2}X^3} {Q^3} }}^{\infty} \!\!\frac{A(n_2,n_1)}{n_1n_2} S\left(-r\bar{a},\pm n_2;\frac{rq}{n_1}\right) V\left(\frac{ n_1^2n_2 Q^3}{r N^{2}X^3}\right) \notag\\&\quad \cdot \sum_{\substack{m\geq1}} \lambda_f(m) e\left(\frac{ma}{q}\right) e\left(\pm 3\frac{m^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \right) m^{-it} W\left(\frac{m}{N}\right) \bigg| + O(T^{-A}). \end{align} $$
$$ \begin{align} S_{r}^{\pm}(N,X,P) & \ll T^{\varepsilon} \bigg| \frac{X}{Q}\sum_{\substack{q\sim P}} \;\frac{1}{q}\; \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} \!\frac{NX}{Q} \sum_{n_1|qr} \sum_{\substack{n_2=1 \\ n_1^2n_2 \asymp \frac{r N^{2}X^3} {Q^3} }}^{\infty} \!\!\frac{A(n_2,n_1)}{n_1n_2} S\left(-r\bar{a},\pm n_2;\frac{rq}{n_1}\right) V\left(\frac{ n_1^2n_2 Q^3}{r N^{2}X^3}\right) \notag\\&\quad \cdot \sum_{\substack{m\geq1}} \lambda_f(m) e\left(\frac{ma}{q}\right) e\left(\pm 3\frac{m^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \right) m^{-it} W\left(\frac{m}{N}\right) \bigg| + O(T^{-A}). \end{align} $$
Here, we have removed the weight function
![]() $V_3$
by the Mellin technique again to separate the variables
$V_3$
by the Mellin technique again to separate the variables
![]() $n_2$
and m, and modified the weight functions W and V accordingly. Note that W and V are
$n_2$
and m, and modified the weight functions W and V accordingly. Note that W and V are
![]() $T^{\varepsilon }$
-inert functions with compact support in
$T^{\varepsilon }$
-inert functions with compact support in
![]() $\mathbb {R}_{>0}$
.
$\mathbb {R}_{>0}$
.
We now apply the Voronoi summation formula (see Lemma 2.4) to the sum over m getting
 $$ \begin{align} \sum_{\substack{m\geq1}} \lambda_f(m) e\left(\frac{ma}{q}\right) e\left(\pm 3\frac{m^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \right) & m^{-it} W\left(\frac{m}{N}\right) \nonumber \\ & = q \sum_{\pm_1} \sum_{m\geq1} \frac{ \lambda_{f}(m) }{m} e\left(\frac{\pm_1\bar{a} m}{q}\right) G^{\pm_1} \left(\frac{m}{q^2} \right), \end{align} $$
$$ \begin{align} \sum_{\substack{m\geq1}} \lambda_f(m) e\left(\frac{ma}{q}\right) e\left(\pm 3\frac{m^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \right) & m^{-it} W\left(\frac{m}{N}\right) \nonumber \\ & = q \sum_{\pm_1} \sum_{m\geq1} \frac{ \lambda_{f}(m) }{m} e\left(\frac{\pm_1\bar{a} m}{q}\right) G^{\pm_1} \left(\frac{m}{q^2} \right), \end{align} $$
where
![]() $g(m)= e\left (\pm 3\frac {m^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \right ) m^{-it} W\left (\frac {m}{N}\right )$
and
$g(m)= e\left (\pm 3\frac {m^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \right ) m^{-it} W\left (\frac {m}{N}\right )$
and
![]() $G^{\pm _1}$
is defined as in (2.8).
$G^{\pm _1}$
is defined as in (2.8).
Lemma 4.2. Assume
![]() $x\asymp X$
and
$x\asymp X$
and
![]() $q\sim P$
. Then
$q\sim P$
. Then
-
i) if
 $yN \gg T^{2+\varepsilon } + (\frac {NX}{PQ})^{2+\varepsilon }$
, then we have
$yN \gg T^{2+\varepsilon } + (\frac {NX}{PQ})^{2+\varepsilon }$
, then we have
 $G^{\pm _1}(y) \ll _A y^{-6} T^{-A}$
;
$G^{\pm _1}(y) \ll _A y^{-6} T^{-A}$
; -
ii) if
 $\frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
, then we have
$\frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
, then we have
 $ G^{\pm _1}(y)$
is equal to (up to an error term of size
$ G^{\pm _1}(y)$
is equal to (up to an error term of size
 $O(T^{-A})$
) for some function
$O(T^{-A})$
) for some function $$\begin{align*}y^{it} (yN)^{1/2} \left( \frac{PQ}{NX}\right)^{1/2} \int_{\mathbb{R}} y^{-i\tau} \left(\frac{ n_1^2n_2}{ q^3} \right)^{i\tau} W_1\left(\frac{ n_1^2n_2 Q^3}{r N^{2}X^3}, \frac{\pm \tau} { \frac{NX}{PQ} } ,\frac{q}{P} \right) w^{\pm_1}(\tau) \mathrm{d} \tau , \end{align*}$$
$$\begin{align*}y^{it} (yN)^{1/2} \left( \frac{PQ}{NX}\right)^{1/2} \int_{\mathbb{R}} y^{-i\tau} \left(\frac{ n_1^2n_2}{ q^3} \right)^{i\tau} W_1\left(\frac{ n_1^2n_2 Q^3}{r N^{2}X^3}, \frac{\pm \tau} { \frac{NX}{PQ} } ,\frac{q}{P} \right) w^{\pm_1}(\tau) \mathrm{d} \tau , \end{align*}$$
 $w^{\pm _1}$
, such that
$w^{\pm _1}$
, such that
 $w^{\pm _1}(\tau )\ll 1$
and some
$w^{\pm _1}(\tau )\ll 1$
and some
 $T^{\varepsilon }$
-inert function
$T^{\varepsilon }$
-inert function
 $W_1$
with compact support in
$W_1$
with compact support in
 $\mathbb {R}_{>0}^3$
;
$\mathbb {R}_{>0}^3$
;
-
iii) if
 $T^{\varepsilon } \ll \frac {NX}{PQ}\ll |T'|^{1-\varepsilon }$
, then
$T^{\varepsilon } \ll \frac {NX}{PQ}\ll |T'|^{1-\varepsilon }$
, then
 $G^{\pm _1}(y) \ll y^{-6} T^{-A}$
is negligibly small unless
$G^{\pm _1}(y) \ll y^{-6} T^{-A}$
is negligibly small unless
 $yN \asymp T|T'|$
, in which case, we have
$yN \asymp T|T'|$
, in which case, we have
 $ G^{\pm _1}(y)$
is equal to (up to an error term of size
$ G^{\pm _1}(y)$
is equal to (up to an error term of size
 $O(T^{-A})$
)where
$O(T^{-A})$
)where $$\begin{align*} \kern-12pt (\pi^2 y)^{it} (Ny)^{1/2} e\left( - \frac{T}{2\pi} \log \frac{T}{2e} - \frac{T'}{2\pi} \log \frac{|T'|}{2e} \pm \frac{B}{2\pi} \sum_{0\leq \ell\leq L} Q_{\ell}^{\pm} \left(\frac{B}{T},\frac{B}{T'} \right) \xi_0^{\ell+1}\right) W_3^{\pm_1}\left( \frac{B} { \frac{NX}{PQ} },\frac{q}{P} \right), \end{align*}$$
$$\begin{align*} \kern-12pt (\pi^2 y)^{it} (Ny)^{1/2} e\left( - \frac{T}{2\pi} \log \frac{T}{2e} - \frac{T'}{2\pi} \log \frac{|T'|}{2e} \pm \frac{B}{2\pi} \sum_{0\leq \ell\leq L} Q_{\ell}^{\pm} \left(\frac{B}{T},\frac{B}{T'} \right) \xi_0^{\ell+1}\right) W_3^{\pm_1}\left( \frac{B} { \frac{NX}{PQ} },\frac{q}{P} \right), \end{align*}$$
 $L=L(A)$
is a large enough integer,
$L=L(A)$
is a large enough integer,
 $Q_{\ell }^{\pm }$
is a certain homogeneous polynomial of degree
$Q_{\ell }^{\pm }$
is a certain homogeneous polynomial of degree
 $\ell $
with
$\ell $
with
 $Q_0^{\pm }\left (\frac {B}{T},\frac {B}{T'} \right ) =3$
and
$Q_0^{\pm }\left (\frac {B}{T},\frac {B}{T'} \right ) =3$
and
 $Q_1^{\pm }\left (\frac {B}{T},\frac {B}{T'} \right ) = \mp \frac {1}{2} \left (\frac {B}{T}+\frac {B}{T'}\right ) $
,
$Q_1^{\pm }\left (\frac {B}{T},\frac {B}{T'} \right ) = \mp \frac {1}{2} \left (\frac {B}{T}+\frac {B}{T'}\right ) $
,
 $B=\frac { N^{1/3} ( n_1^2n_2)^{1/3} }{ r^{1/3} q}\asymp \frac {NX}{PQ} $
,
$B=\frac { N^{1/3} ( n_1^2n_2)^{1/3} }{ r^{1/3} q}\asymp \frac {NX}{PQ} $
,
 $\xi _0 = \left (\frac {2\pi T|T'|}{yN}\right )^{1/3} \asymp 1$
, and
$\xi _0 = \left (\frac {2\pi T|T'|}{yN}\right )^{1/3} \asymp 1$
, and
 $W_3^{\pm _1}$
is a
$W_3^{\pm _1}$
is a
 $T^{\varepsilon }$
-inert function with compact support in
$T^{\varepsilon }$
-inert function with compact support in
 $\mathbb {R}_{>0}^2$
.
$\mathbb {R}_{>0}^2$
.
Proof. (i) First, we use the second expression in (2.8), getting
 $$ \begin{align*} G^{\pm_1}(y) = \epsilon_f^{(1\mp_1 1)/2} y \int_{0}^{\infty} e\left(\pm 3\frac{u^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \right) u^{-it} W\left(\frac{u}{N}\right) V\left(\frac{ n_1^2n_2 Q^3}{r u^{2}X^3}\right) J^{\pm_1}_{f}\left( 4\pi\sqrt{yu} \right) \mathrm{d} u. \end{align*} $$
$$ \begin{align*} G^{\pm_1}(y) = \epsilon_f^{(1\mp_1 1)/2} y \int_{0}^{\infty} e\left(\pm 3\frac{u^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \right) u^{-it} W\left(\frac{u}{N}\right) V\left(\frac{ n_1^2n_2 Q^3}{r u^{2}X^3}\right) J^{\pm_1}_{f}\left( 4\pi\sqrt{yu} \right) \mathrm{d} u. \end{align*} $$
Making a change of variable
![]() $u=N\xi $
, we have
$u=N\xi $
, we have
![]() $G^{\pm _1}(y)$
is equal to
$G^{\pm _1}(y)$
is equal to
 $$ \begin{align*} \epsilon_f^{(1\mp_1 1)/2} y N^{1-it} \int_{0}^{\infty} e\left(\pm 3\frac{N^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \xi^{1/3} \right) \xi^{-it} W\left(\xi\right) V\left(\frac{ n_1^2n_2 Q^3}{r N^2 \xi^{2}X^3}\right) J^{\pm_1}_{f}\left( 4\pi\sqrt{yN\xi} \right) \mathrm{d} \xi. \end{align*} $$
$$ \begin{align*} \epsilon_f^{(1\mp_1 1)/2} y N^{1-it} \int_{0}^{\infty} e\left(\pm 3\frac{N^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \xi^{1/3} \right) \xi^{-it} W\left(\xi\right) V\left(\frac{ n_1^2n_2 Q^3}{r N^2 \xi^{2}X^3}\right) J^{\pm_1}_{f}\left( 4\pi\sqrt{yN\xi} \right) \mathrm{d} \xi. \end{align*} $$
If
![]() $yN\gg t_f^{2}T^{\varepsilon }$
, then by (2.17), we have
$yN\gg t_f^{2}T^{\varepsilon }$
, then by (2.17), we have
![]() $G^{-}(y) \ll _A y^{-6} T^{-A}$
for any
$G^{-}(y) \ll _A y^{-6} T^{-A}$
for any
![]() $A>0$
. If
$A>0$
. If
![]() $yN\gg T^{2+\varepsilon } + (\frac {NX}{PQ})^{2+\varepsilon }$
, then by (2.15), we have
$yN\gg T^{2+\varepsilon } + (\frac {NX}{PQ})^{2+\varepsilon }$
, then by (2.15), we have
 $$ \begin{align*} G^+(y) &= y N^{1-it} \int_{0}^{\infty} e\left(\pm 3\frac{N^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \xi^{1/3} \right) \xi^{-it} W\left(\xi\right) V\left(\frac{ n_1^2n_2 Q^3}{r N^2 \xi^{2}X^3}\right) \\&\quad\cdot \sum_{\pm} e^{\pm 2i \omega(2\pi\sqrt{yN\xi},t_f)} \frac{g_A^{\pm}(2\pi\sqrt{yN\xi},t_f)}{(2\pi\sqrt{yN\xi})^{1/2}+t_f^{1/2}} \mathrm{d} \xi + O_A(y^{-6} T^{-A}). \end{align*} $$
$$ \begin{align*} G^+(y) &= y N^{1-it} \int_{0}^{\infty} e\left(\pm 3\frac{N^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \xi^{1/3} \right) \xi^{-it} W\left(\xi\right) V\left(\frac{ n_1^2n_2 Q^3}{r N^2 \xi^{2}X^3}\right) \\&\quad\cdot \sum_{\pm} e^{\pm 2i \omega(2\pi\sqrt{yN\xi},t_f)} \frac{g_A^{\pm}(2\pi\sqrt{yN\xi},t_f)}{(2\pi\sqrt{yN\xi})^{1/2}+t_f^{1/2}} \mathrm{d} \xi + O_A(y^{-6} T^{-A}). \end{align*} $$
Let (temporarily)
 $$\begin{align*}h(\xi) = \pm 6\pi\frac{N^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \xi^{1/3} -t\log \xi \pm 2 \omega(2\pi\sqrt{yN\xi},t_f). \end{align*}$$
$$\begin{align*}h(\xi) = \pm 6\pi\frac{N^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \xi^{1/3} -t\log \xi \pm 2 \omega(2\pi\sqrt{yN\xi},t_f). \end{align*}$$
Then we have
 $$\begin{align*}h'(\xi) = \pm 2\pi\frac{N^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \xi^{-2/3} -\frac{t}{\xi} \mp \frac{\sqrt{(2\pi\sqrt{yN\xi})^2+t_f^2}}{\xi} \gg (yN)^{1/2}, \end{align*}$$
$$\begin{align*}h'(\xi) = \pm 2\pi\frac{N^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \xi^{-2/3} -\frac{t}{\xi} \mp \frac{\sqrt{(2\pi\sqrt{yN\xi})^2+t_f^2}}{\xi} \gg (yN)^{1/2}, \end{align*}$$
By Lemma 2.7 with
we get
![]() $G^+(y) \ll _A y^{-6} T^{-A}$
. Hence, we have
$G^+(y) \ll _A y^{-6} T^{-A}$
. Hence, we have
![]() $G^{\pm _1}(y) \ll _A y^{-6} T^{-A}$
if
$G^{\pm _1}(y) \ll _A y^{-6} T^{-A}$
if
![]() $yN\gg T^{2+\varepsilon } + (\frac {NX}{PQ})^{2+\varepsilon }$
.
$yN\gg T^{2+\varepsilon } + (\frac {NX}{PQ})^{2+\varepsilon }$
.
(ii) For
![]() $yN \ll T^{2+\varepsilon } + (\frac {NX}{PQ})^{2+\varepsilon }$
, we use the first expression in (2.8). Writing
$yN \ll T^{2+\varepsilon } + (\frac {NX}{PQ})^{2+\varepsilon }$
, we use the first expression in (2.8). Writing
![]() $s=\sigma +i\tau $
with
$s=\sigma +i\tau $
with
![]() $\sigma =-1/2$
and making a change of variable
$\sigma =-1/2$
and making a change of variable
![]() $\tau \rightsquigarrow \tau -t$
, we get
$\tau \rightsquigarrow \tau -t$
, we get
 $$ \begin{align} G^{\pm_1}(y) = \frac{\epsilon_f^{(1\mp_1 1)/2}}{4\pi^2} \int_{\mathbb{R}} (\pi^2 y)^{1/2-i\tau+it} \gamma_2^{\pm_1}(-1/2+i\tau-it) \tilde{g}(1/2-i\tau+it) \mathrm{d} \tau, \end{align} $$
$$ \begin{align} G^{\pm_1}(y) = \frac{\epsilon_f^{(1\mp_1 1)/2}}{4\pi^2} \int_{\mathbb{R}} (\pi^2 y)^{1/2-i\tau+it} \gamma_2^{\pm_1}(-1/2+i\tau-it) \tilde{g}(1/2-i\tau+it) \mathrm{d} \tau, \end{align} $$
where
 $$\begin{align*}\gamma_2^{\pm_1}(-1/2+i\tau-it) = \frac{\Gamma(\frac{1/2+i\tau-iT}{2})\Gamma(\frac{1/2+i\tau-iT'}{2})} {\Gamma(\frac{1/2-i\tau+iT}{2})\Gamma(\frac{1/2-i\tau+iT'}{2})} \pm_1 \frac{\Gamma(\frac{3/2+i\tau-iT}{2})\Gamma(\frac{3/2+i\tau-iT'}{2})} {\Gamma(\frac{3/2-i\tau+iT}{2})\Gamma(\frac{3/2-i\tau+iT'}{2})}. \end{align*}$$
$$\begin{align*}\gamma_2^{\pm_1}(-1/2+i\tau-it) = \frac{\Gamma(\frac{1/2+i\tau-iT}{2})\Gamma(\frac{1/2+i\tau-iT'}{2})} {\Gamma(\frac{1/2-i\tau+iT}{2})\Gamma(\frac{1/2-i\tau+iT'}{2})} \pm_1 \frac{\Gamma(\frac{3/2+i\tau-iT}{2})\Gamma(\frac{3/2+i\tau-iT'}{2})} {\Gamma(\frac{3/2-i\tau+iT}{2})\Gamma(\frac{3/2-i\tau+iT'}{2})}. \end{align*}$$
If
![]() $\frac {NX}{PQ}\gg T^{\varepsilon }$
, then
$\frac {NX}{PQ}\gg T^{\varepsilon }$
, then
 $$ \begin{align*} \tilde{g}(1/2-i\tau+it) = \int_{\mathbb{R}} e\left(\pm 3\frac{u^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \right) W\left(\frac{u}{N}\right) u^{-1/2-i\tau} \mathrm{d} u. \end{align*} $$
$$ \begin{align*} \tilde{g}(1/2-i\tau+it) = \int_{\mathbb{R}} e\left(\pm 3\frac{u^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \right) W\left(\frac{u}{N}\right) u^{-1/2-i\tau} \mathrm{d} u. \end{align*} $$
Making a change of variable
![]() $u=N\xi ^3$
, we have
$u=N\xi ^3$
, we have
 $$ \begin{align*} \tilde{g}(1/2-i\tau+it) = N^{1/2-i\tau} \int_{\mathbb{R}} e\left(\pm 3\frac{N^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \xi - \frac{3 \tau}{2\pi} \log \xi \right) W\left(\xi^3\right) 3 \xi^{1/2} \mathrm{d} \xi. \end{align*} $$
$$ \begin{align*} \tilde{g}(1/2-i\tau+it) = N^{1/2-i\tau} \int_{\mathbb{R}} e\left(\pm 3\frac{N^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \xi - \frac{3 \tau}{2\pi} \log \xi \right) W\left(\xi^3\right) 3 \xi^{1/2} \mathrm{d} \xi. \end{align*} $$
Let (temporarily)
 $$\begin{align*}h(\xi) = \pm 3\frac{N^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \xi - \frac{3\tau}{2\pi} \log \xi. \end{align*}$$
$$\begin{align*}h(\xi) = \pm 3\frac{N^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \xi - \frac{3\tau}{2\pi} \log \xi. \end{align*}$$
Then
 $$\begin{align*}h'(\xi) = \pm 3 \frac{N^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} - \frac{3 \tau}{2\pi \xi} , \end{align*}$$
$$\begin{align*}h'(\xi) = \pm 3 \frac{N^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} - \frac{3 \tau}{2\pi \xi} , \end{align*}$$
and
By Lemma 2.7 with
we have
![]() $\tilde {g}(1/2-i\tau +it)$
is negligibly small unless
$\tilde {g}(1/2-i\tau +it)$
is negligibly small unless
![]() $\operatorname {sgn}(\tau )=\pm $
and
$\operatorname {sgn}(\tau )=\pm $
and
![]() $\tau \asymp \frac {N^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \asymp \frac {NX}{PQ}$
, in which case, the solution of
$\tau \asymp \frac {N^{1/3} ( n_1^2n_2)^{1/3} }{r^{1/3} q} \asymp \frac {NX}{PQ}$
, in which case, the solution of
![]() $h'(\xi )=0$
is
$h'(\xi )=0$
is
 $$\begin{align*}\xi_0 = \frac{\pm \tau}{2\pi } \frac{r^{1/3} q} {N^{1/3} ( n_1^2n_2)^{1/3} }. \end{align*}$$
$$\begin{align*}\xi_0 = \frac{\pm \tau}{2\pi } \frac{r^{1/3} q} {N^{1/3} ( n_1^2n_2)^{1/3} }. \end{align*}$$
Note that
 $$\begin{align*}h(\xi_0) = -\frac{3\tau}{2\pi} \log \frac{\pm \tau r^{1/3} q} {2\pi e N^{1/3} ( n_1^2n_2)^{1/3} }. \end{align*}$$
$$\begin{align*}h(\xi_0) = -\frac{3\tau}{2\pi} \log \frac{\pm \tau r^{1/3} q} {2\pi e N^{1/3} ( n_1^2n_2)^{1/3} }. \end{align*}$$
Now, by Lemma 2.8 with
 $$\begin{align*}X= T^{\varepsilon}, t_1=\xi, t_2=n_1^2n_2, t_3=\tau, t_4=q, X_1=1, X_2=\frac{rN^2X^3}{Q^3}, X_3=\frac{NX}{PQ}, X_4=P, \text{ and } Y=\frac{NX}{PQ}, \end{align*}$$
$$\begin{align*}X= T^{\varepsilon}, t_1=\xi, t_2=n_1^2n_2, t_3=\tau, t_4=q, X_1=1, X_2=\frac{rN^2X^3}{Q^3}, X_3=\frac{NX}{PQ}, X_4=P, \text{ and } Y=\frac{NX}{PQ}, \end{align*}$$
we get
 $$ \begin{align} \tilde{g}(1/2-i\tau+it) = N^{1/2-i\tau} \left(\frac{NX}{PQ}\right)^{-1/2} e\left(-\frac{3\tau}{2\pi} \log \frac{\pm \tau } {2\pi e B }\right) W_1\left(\frac{ n_1^2n_2 Q^3}{r N^{2}X^3}, \frac{\pm \tau} { \frac{NX}{PQ} } ,\frac{q}{P} \right) + O_A(T^{-A}), \end{align} $$
$$ \begin{align} \tilde{g}(1/2-i\tau+it) = N^{1/2-i\tau} \left(\frac{NX}{PQ}\right)^{-1/2} e\left(-\frac{3\tau}{2\pi} \log \frac{\pm \tau } {2\pi e B }\right) W_1\left(\frac{ n_1^2n_2 Q^3}{r N^{2}X^3}, \frac{\pm \tau} { \frac{NX}{PQ} } ,\frac{q}{P} \right) + O_A(T^{-A}), \end{align} $$
where
![]() $B=\frac { N^{1/3} ( n_1^2n_2)^{1/3} }{ r^{1/3} q} $
and
$B=\frac { N^{1/3} ( n_1^2n_2)^{1/3} }{ r^{1/3} q} $
and
![]() $W_1$
is a
$W_1$
is a
![]() $T^{\varepsilon }$
-inert function with compact support in
$T^{\varepsilon }$
-inert function with compact support in
![]() $\mathbb {R}_{>0}^3$
. Note that we have
$\mathbb {R}_{>0}^3$
. Note that we have
![]() $B \asymp \frac {NX}{PQ}$
.
$B \asymp \frac {NX}{PQ}$
.
Now, we consider the case
![]() $ \frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
. By (4.4) and (4.5), we have
$ \frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
. By (4.4) and (4.5), we have
 $$ \begin{align} G^{\pm_1}(y) &= \frac{\epsilon_f^{(1\mp_1 1)/2}}{4\pi} (\pi^2 y)^{it} (yN)^{1/2} \left(\frac{NX}{PQ}\right)^{-1/2}\!\! \int_{\mathbb{R}} (\pi^2 yN )^{-i\tau} \left(\frac{ N n_1^2n_2}{ r q^3} \right)^{i\tau}\! W_1\!\left(\frac{ n_1^2n_2 Q^3}{r N^{2}X^3}, \frac{\pm \tau} { \frac{NX}{PQ} } ,\frac{q}{P} \right)\notag \\&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \ \cdot \gamma_2^{\pm_1}(-1/2+i\tau-it) e\left(-\frac{3\tau}{2\pi} \log \frac{\pm \tau } {2\pi e}\right) \mathrm{d} \tau + O(T^{-A}). \end{align} $$
$$ \begin{align} G^{\pm_1}(y) &= \frac{\epsilon_f^{(1\mp_1 1)/2}}{4\pi} (\pi^2 y)^{it} (yN)^{1/2} \left(\frac{NX}{PQ}\right)^{-1/2}\!\! \int_{\mathbb{R}} (\pi^2 yN )^{-i\tau} \left(\frac{ N n_1^2n_2}{ r q^3} \right)^{i\tau}\! W_1\!\left(\frac{ n_1^2n_2 Q^3}{r N^{2}X^3}, \frac{\pm \tau} { \frac{NX}{PQ} } ,\frac{q}{P} \right)\notag \\&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \ \cdot \gamma_2^{\pm_1}(-1/2+i\tau-it) e\left(-\frac{3\tau}{2\pi} \log \frac{\pm \tau } {2\pi e}\right) \mathrm{d} \tau + O(T^{-A}). \end{align} $$
Taking
![]() $w^{\pm _1}(\tau ) = \frac {\epsilon _f^{(1\mp _1 1)/2}}{4\pi } \pi ^{2it} (\pi ^2 r)^{-i\tau } \gamma _2^{\pm _1}(-1/2+i\tau -it) e\left (-\frac {3\tau }{2\pi } \log \frac {\pm \tau } {2\pi e}\right )$
, and noting that
$w^{\pm _1}(\tau ) = \frac {\epsilon _f^{(1\mp _1 1)/2}}{4\pi } \pi ^{2it} (\pi ^2 r)^{-i\tau } \gamma _2^{\pm _1}(-1/2+i\tau -it) e\left (-\frac {3\tau }{2\pi } \log \frac {\pm \tau } {2\pi e}\right )$
, and noting that
![]() $w^{\pm _1}(\tau )\ll 1$
, we complete the proof of Lemma 4.2 (ii).
$w^{\pm _1}(\tau )\ll 1$
, we complete the proof of Lemma 4.2 (ii).
(iii) We now consider the case
![]() $T^{\varepsilon } \ll \frac {NX}{PQ}\ll |T'|^{1-\varepsilon }$
. By Stirling’s formula, for
$T^{\varepsilon } \ll \frac {NX}{PQ}\ll |T'|^{1-\varepsilon }$
. By Stirling’s formula, for
![]() $\tau \ll |T'|^{1-\varepsilon }$
, we have
$\tau \ll |T'|^{1-\varepsilon }$
, we have
 $$ \begin{align*} \gamma_2^{\pm_1}(-1/2+i\tau-it)& = \exp\left( i(\tau-T)\log\frac{T-\tau}{2e} + i(\tau-T')\log\frac{|T'-\tau|}{2e} \right) \\ &\qquad\qquad\qquad\qquad\qquad\qquad\cdot \left( w_{\epsilon_f,J}^{\pm_1}(\tau-T) w_{\epsilon_f,J}^{\pm_1}(\tau-T') + O_{J}(T^{-J}) \right), \end{align*} $$
$$ \begin{align*} \gamma_2^{\pm_1}(-1/2+i\tau-it)& = \exp\left( i(\tau-T)\log\frac{T-\tau}{2e} + i(\tau-T')\log\frac{|T'-\tau|}{2e} \right) \\ &\qquad\qquad\qquad\qquad\qquad\qquad\cdot \left( w_{\epsilon_f,J}^{\pm_1}(\tau-T) w_{\epsilon_f,J}^{\pm_1}(\tau-T') + O_{J}(T^{-J}) \right), \end{align*} $$
where
for all fixed
![]() $j\in \mathbb {N}_0$
. Hence, together with (4.4) and (4.5), we have
$j\in \mathbb {N}_0$
. Hence, together with (4.4) and (4.5), we have
 $$ \begin{align*} &G^{\pm_1}(y) = \frac{\epsilon_f^{(1\mp_1 1)/2}}{4\pi } (\pi^2 y)^{it} (Ny)^{1/2} \left(\frac{NX}{PQ}\right)^{-1/2} \!\!\int_{\mathbb{R}} w_{\epsilon_f,J}^{\pm_1}\left(\tau - T\right) w_{\epsilon_f,J}^{\pm_1}\left(\tau-T'\right) W_1\!\left(\frac{B^3 q^3 Q^3}{N^{3}X^3}, \frac{\pm \tau} { \frac{NX}{PQ} } , \frac{q}{P}\right) \\&\quad\cdot e\left( - \frac{\tau}{2\pi} \log(\pi^2 yN) + \frac{(\tau - T)}{2\pi}\log\frac{T-\tau}{2e} + \frac{(\tau - T')}{2\pi}\log\frac{|T'-\tau|}{2e} -\frac{3\tau}{2\pi} \log \frac{\pm \tau } {2\pi e B } \right) \mathrm{d} \tau + O_A(T^{-A}). \end{align*} $$
$$ \begin{align*} &G^{\pm_1}(y) = \frac{\epsilon_f^{(1\mp_1 1)/2}}{4\pi } (\pi^2 y)^{it} (Ny)^{1/2} \left(\frac{NX}{PQ}\right)^{-1/2} \!\!\int_{\mathbb{R}} w_{\epsilon_f,J}^{\pm_1}\left(\tau - T\right) w_{\epsilon_f,J}^{\pm_1}\left(\tau-T'\right) W_1\!\left(\frac{B^3 q^3 Q^3}{N^{3}X^3}, \frac{\pm \tau} { \frac{NX}{PQ} } , \frac{q}{P}\right) \\&\quad\cdot e\left( - \frac{\tau}{2\pi} \log(\pi^2 yN) + \frac{(\tau - T)}{2\pi}\log\frac{T-\tau}{2e} + \frac{(\tau - T')}{2\pi}\log\frac{|T'-\tau|}{2e} -\frac{3\tau}{2\pi} \log \frac{\pm \tau } {2\pi e B } \right) \mathrm{d} \tau + O_A(T^{-A}). \end{align*} $$
Making a change of variable
![]() $\tau = \pm B \xi $
, we get
$\tau = \pm B \xi $
, we get
 $$ \begin{align*} G^{\pm_1}(y) &= (\pi^2 y)^{it} (Ny)^{1/2} \left(\frac{NX}{PQ}\right)^{1/2} \int_{\mathbb{R}} W_2^{\pm_1}\left(\xi, \frac{B} { \frac{NX}{PQ} },\frac{q}{P} \right) e\bigg( \mp \frac{B\xi}{2\pi} \log (\pi^2 yN) \mp \frac{3B\xi}{2\pi} \log \frac{\xi}{2\pi e} \\&\qquad\qquad\qquad\quad \ + \frac{(\pm B \xi - T )}{2\pi}\log\frac{T\mp B \xi}{2e} + \frac{(\pm B \xi - T')}{2\pi}\log\frac{|T'\mp B \xi|}{2e} \bigg) \mathrm{d} \xi + O_A(T^{-A}), \end{align*} $$
$$ \begin{align*} G^{\pm_1}(y) &= (\pi^2 y)^{it} (Ny)^{1/2} \left(\frac{NX}{PQ}\right)^{1/2} \int_{\mathbb{R}} W_2^{\pm_1}\left(\xi, \frac{B} { \frac{NX}{PQ} },\frac{q}{P} \right) e\bigg( \mp \frac{B\xi}{2\pi} \log (\pi^2 yN) \mp \frac{3B\xi}{2\pi} \log \frac{\xi}{2\pi e} \\&\qquad\qquad\qquad\quad \ + \frac{(\pm B \xi - T )}{2\pi}\log\frac{T\mp B \xi}{2e} + \frac{(\pm B \xi - T')}{2\pi}\log\frac{|T'\mp B \xi|}{2e} \bigg) \mathrm{d} \xi + O_A(T^{-A}), \end{align*} $$
where
 $W_2^{\pm _1}\left (\xi , \frac {B} { \frac {NX}{PQ} },\frac {q}{P} \right ) = \frac {\epsilon _f^{(1\mp _1 1)/2}}{4\pi } w_{\epsilon _f,J}^{\pm _1}\left (\pm B \xi - T\right ) w_{\epsilon _f,J}^{\pm _1}\left (\pm B \xi -T'\right ) W_1\left (\frac {B^3 q^3 Q^3}{N^{3}X^3}, \frac {B \xi } { \frac {NX}{PQ} } , \frac {q}{P}\right ) \frac {B}{\frac {NX}{PQ} } $
is a
$W_2^{\pm _1}\left (\xi , \frac {B} { \frac {NX}{PQ} },\frac {q}{P} \right ) = \frac {\epsilon _f^{(1\mp _1 1)/2}}{4\pi } w_{\epsilon _f,J}^{\pm _1}\left (\pm B \xi - T\right ) w_{\epsilon _f,J}^{\pm _1}\left (\pm B \xi -T'\right ) W_1\left (\frac {B^3 q^3 Q^3}{N^{3}X^3}, \frac {B \xi } { \frac {NX}{PQ} } , \frac {q}{P}\right ) \frac {B}{\frac {NX}{PQ} } $
is a
![]() $T^{\varepsilon }$
-inert function with compact support in
$T^{\varepsilon }$
-inert function with compact support in
![]() $\mathbb {R}_{>0}^3$
. Let (temporarily)
$\mathbb {R}_{>0}^3$
. Let (temporarily)
Then
 $$ \begin{align*} h'(\xi) & =\mp \frac{B}{2\pi} \log (\pi^2 yN) \mp \frac{3B}{2\pi} \log \frac{\xi}{2\pi} + \frac{\pm B}{2\pi}\log\frac{T\mp B \xi}{2} + \frac{\pm B}{2\pi}\log\frac{|T'\mp B \xi|}{2} \\ & = \mp \frac{B}{2\pi} \log \frac{yN \xi^3}{2\pi (T\mp B \xi)|T'\mp B \xi|} , \end{align*} $$
$$ \begin{align*} h'(\xi) & =\mp \frac{B}{2\pi} \log (\pi^2 yN) \mp \frac{3B}{2\pi} \log \frac{\xi}{2\pi} + \frac{\pm B}{2\pi}\log\frac{T\mp B \xi}{2} + \frac{\pm B}{2\pi}\log\frac{|T'\mp B \xi|}{2} \\ & = \mp \frac{B}{2\pi} \log \frac{yN \xi^3}{2\pi (T\mp B \xi)|T'\mp B \xi|} , \end{align*} $$
and
By Lemma 2.7 with
we have that
![]() $G^{\pm _1}(y) \ll _A T^{-A}$
is negligibly small unless
$G^{\pm _1}(y) \ll _A T^{-A}$
is negligibly small unless
![]() $yN \asymp T |T'|$
. Assume
$yN \asymp T |T'|$
. Assume
![]() $yN \asymp T |T'|$
. Denote the solution of
$yN \asymp T |T'|$
. Denote the solution of
![]() $h'(\xi )=0$
by
$h'(\xi )=0$
by
![]() $\xi _*$
with
$\xi _*$
with
![]() $\xi _*\asymp 1$
. Then by Lemma 2.8 with
$\xi _*\asymp 1$
. Then by Lemma 2.8 with
we get
 $$ \begin{align} G^{\pm_1}(y) & = (\pi^2 y)^{it} (Ny)^{1/2} e(h(\xi_*)) W_3^{\pm_1}\left( \frac{B} { \frac{NX}{PQ} },\frac{q}{P},\frac{yN}{T|T'|} \right) + O_A(T^{-A}), \end{align} $$
$$ \begin{align} G^{\pm_1}(y) & = (\pi^2 y)^{it} (Ny)^{1/2} e(h(\xi_*)) W_3^{\pm_1}\left( \frac{B} { \frac{NX}{PQ} },\frac{q}{P},\frac{yN}{T|T'|} \right) + O_A(T^{-A}), \end{align} $$
where
![]() $W_3^{\pm _1}$
is a
$W_3^{\pm _1}$
is a
![]() $T^{\varepsilon }$
-inert function with compact support in
$T^{\varepsilon }$
-inert function with compact support in
![]() $\mathbb {R}_{>0}^3$
. Note that the assumptions in Lemma 2.8 hold in this case.
$\mathbb {R}_{>0}^3$
. Note that the assumptions in Lemma 2.8 hold in this case.
We now simplify the expression of
![]() $G^{\pm _1}(y)$
. Note that the solution of
$G^{\pm _1}(y)$
. Note that the solution of
![]() $h'(\xi )=0$
, that is,
$h'(\xi )=0$
, that is,
![]() $yN\xi ^3=2\pi T|T'|(1\mp \frac {B}{T}\xi )(1\mp \frac {B}{T'}\xi )$
, can be written as
$yN\xi ^3=2\pi T|T'|(1\mp \frac {B}{T}\xi )(1\mp \frac {B}{T'}\xi )$
, can be written as
where
![]() $L \geq 3$
is a large integer and
$L \geq 3$
is a large integer and
![]() $\xi _{\ell +1}=o(\xi _{\ell })$
(
$\xi _{\ell +1}=o(\xi _{\ell })$
(
![]() $0\leq \ell \leq L$
) with
$0\leq \ell \leq L$
) with
 $$\begin{align*}\xi_0 = \left(\frac{2\pi T|T'|}{yN}\right)^{1/3}, \quad \xi_1 = \frac{1}{3} \left(\mp \frac{B}{T}\mp \frac{B}{T'}\right) \xi_0^2, \quad \xi_2 = \frac{B^2}{3TT'} \xi_0^3, \end{align*}$$
$$\begin{align*}\xi_0 = \left(\frac{2\pi T|T'|}{yN}\right)^{1/3}, \quad \xi_1 = \frac{1}{3} \left(\mp \frac{B}{T}\mp \frac{B}{T'}\right) \xi_0^2, \quad \xi_2 = \frac{B^2}{3TT'} \xi_0^3, \end{align*}$$
and
![]() $\xi _{\ell }$
(
$\xi _{\ell }$
(
![]() $2<\ell \leq L$
) is the solution of
$2<\ell \leq L$
) is the solution of
 $$ \begin{align*} \xi_0^{-3} \sum_{\substack{0\leq i,j,k\leq \ell \\ i+j+k\leq \ell}} \xi_i\xi_j\xi_k = 1\mp \left(\frac{B}{T}+\frac{B}{T'}\right)\sum_{0\leq i\leq \ell-1} \xi_i + \frac{B^2}{TT'} \sum_{\substack{0\leq i,j\leq \ell-2 \\ i+j\leq \ell-2}} \xi_i\xi_j. \end{align*} $$
$$ \begin{align*} \xi_0^{-3} \sum_{\substack{0\leq i,j,k\leq \ell \\ i+j+k\leq \ell}} \xi_i\xi_j\xi_k = 1\mp \left(\frac{B}{T}+\frac{B}{T'}\right)\sum_{0\leq i\leq \ell-1} \xi_i + \frac{B^2}{TT'} \sum_{\substack{0\leq i,j\leq \ell-2 \\ i+j\leq \ell-2}} \xi_i\xi_j. \end{align*} $$
Note that
 $$\begin{align*}\xi_{\ell} = \frac{\xi_0}{3} \bigg( \mp \left(\frac{B}{T}+\frac{B}{T'}\right) \xi_{\ell-1} + \frac{B^2}{TT'} \sum_{\substack{0\leq i,j\leq \ell-2 \\ i+j= \ell-2}} \xi_i\xi_j - \xi_0^{-3} \sum_{\substack{0\leq i,j,k\leq \ell-1 \\ i+j+k=\ell}} \xi_i\xi_j\xi_k \bigg), \quad \ell \leq L. \end{align*}$$
$$\begin{align*}\xi_{\ell} = \frac{\xi_0}{3} \bigg( \mp \left(\frac{B}{T}+\frac{B}{T'}\right) \xi_{\ell-1} + \frac{B^2}{TT'} \sum_{\substack{0\leq i,j\leq \ell-2 \\ i+j= \ell-2}} \xi_i\xi_j - \xi_0^{-3} \sum_{\substack{0\leq i,j,k\leq \ell-1 \\ i+j+k=\ell}} \xi_i\xi_j\xi_k \bigg), \quad \ell \leq L. \end{align*}$$
By induction, we have
 $$\begin{align*}\xi_{\ell} = P_{\ell}\left(\frac{B}{T},\frac{B}{T'} \right) \xi_0^{\ell+1} = O_L\left( \frac{B^{\ell}}{|T'|^{\ell}} \right), \quad 0\leq \ell\leq L, \quad \textrm{and} \quad \xi_{L+1} \ll_L \frac{B^{L+1}}{|T'|^{L+1}}, \end{align*}$$
$$\begin{align*}\xi_{\ell} = P_{\ell}\left(\frac{B}{T},\frac{B}{T'} \right) \xi_0^{\ell+1} = O_L\left( \frac{B^{\ell}}{|T'|^{\ell}} \right), \quad 0\leq \ell\leq L, \quad \textrm{and} \quad \xi_{L+1} \ll_L \frac{B^{L+1}}{|T'|^{L+1}}, \end{align*}$$
where
![]() $P_{\ell }$
is a certain homogeneous polynomial of degree
$P_{\ell }$
is a certain homogeneous polynomial of degree
![]() $\ell $
. Note that
$\ell $
. Note that
 $$ \begin{align*} h(\xi_*) & = \mp \frac{B\xi_*}{2\pi} \log \left( \frac{yN \xi_*^3}{2\pi e (T \mp B \xi_*)|T'\mp B\xi_*|} \right) - \frac{T}{2\pi} \log \frac{T\mp B \xi_*}{2e} - \frac{T'}{2\pi} \log \frac{|T'\mp B \xi_*|}{2e}. \end{align*} $$
$$ \begin{align*} h(\xi_*) & = \mp \frac{B\xi_*}{2\pi} \log \left( \frac{yN \xi_*^3}{2\pi e (T \mp B \xi_*)|T'\mp B\xi_*|} \right) - \frac{T}{2\pi} \log \frac{T\mp B \xi_*}{2e} - \frac{T'}{2\pi} \log \frac{|T'\mp B \xi_*|}{2e}. \end{align*} $$
Note that
![]() $\xi _*\asymp 1$
and
$\xi _*\asymp 1$
and
![]() $B/T=o(1)$
. By the Taylor expansion, we get
$B/T=o(1)$
. By the Taylor expansion, we get
 $$ \begin{align*} h(\xi_*) & = - \frac{T}{2\pi} \log \frac{T}{2e} - \frac{T'}{2\pi} \log \frac{|T'|}{2e} \pm \frac{B}{2\pi} \xi_* + \frac{1}{2\pi} \sum_{j\geq1} \frac{1}{j} \left(\frac{(\pm B)^{j}}{T^{j-1}}+\frac{(\pm B)^{j}}{T^{\prime j-1}}\right) \xi_*^{j} \\ & = - \frac{T}{2\pi} \log \frac{T}{2e} - \frac{T'}{2\pi} \log \frac{|T'|}{2e} \pm \frac{B}{2\pi} \sum_{0\leq \ell\leq L} Q_{\ell}^{\pm} \left(\frac{B}{T},\frac{B}{T'} \right) \xi_0^{\ell+1} + O_L\left( \frac{B^{L+2}}{|T'|^{L+1}} \right), \end{align*} $$
$$ \begin{align*} h(\xi_*) & = - \frac{T}{2\pi} \log \frac{T}{2e} - \frac{T'}{2\pi} \log \frac{|T'|}{2e} \pm \frac{B}{2\pi} \xi_* + \frac{1}{2\pi} \sum_{j\geq1} \frac{1}{j} \left(\frac{(\pm B)^{j}}{T^{j-1}}+\frac{(\pm B)^{j}}{T^{\prime j-1}}\right) \xi_*^{j} \\ & = - \frac{T}{2\pi} \log \frac{T}{2e} - \frac{T'}{2\pi} \log \frac{|T'|}{2e} \pm \frac{B}{2\pi} \sum_{0\leq \ell\leq L} Q_{\ell}^{\pm} \left(\frac{B}{T},\frac{B}{T'} \right) \xi_0^{\ell+1} + O_L\left( \frac{B^{L+2}}{|T'|^{L+1}} \right), \end{align*} $$
where
![]() $Q_{\ell }^{\pm }$
is a certain homogeneous polynomial of degree
$Q_{\ell }^{\pm }$
is a certain homogeneous polynomial of degree
![]() $\ell $
. Note that we have
$\ell $
. Note that we have
![]() $Q_0^{\pm }\left (\frac {B}{T},\frac {B}{T'} \right ) =3$
and
$Q_0^{\pm }\left (\frac {B}{T},\frac {B}{T'} \right ) =3$
and
![]() $Q_1^{\pm }\left (\frac {B}{T},\frac {B}{T'} \right ) = \mp \frac {1}{2} \left (\frac {B}{T}+\frac {B}{T'}\right ) $
. Hence, by (4.7), we get
$Q_1^{\pm }\left (\frac {B}{T},\frac {B}{T'} \right ) = \mp \frac {1}{2} \left (\frac {B}{T}+\frac {B}{T'}\right ) $
. Hence, by (4.7), we get
 $$ \begin{align*} G^{\pm_1}(y) &= (\pi^2 y)^{it} (Ny)^{1/2} e\bigg( - \frac{T}{2\pi} \log \frac{T}{2e} - \frac{T'}{2\pi} \log \frac{|T'|}{2e} \pm \frac{B}{2\pi} \sum_{0\leq \ell\leq L} Q_{\ell}^{\pm} \left(\frac{B}{T},\frac{B}{T'} \right) \xi_0^{\ell+1}\bigg) \\&\quad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \ \cdot W_3^{\pm_1}\left( \frac{B} { \frac{NX}{PQ} },\frac{q}{P},\frac{yN}{T|T'|} \right) + O_A(T^{-A}). \end{align*} $$
$$ \begin{align*} G^{\pm_1}(y) &= (\pi^2 y)^{it} (Ny)^{1/2} e\bigg( - \frac{T}{2\pi} \log \frac{T}{2e} - \frac{T'}{2\pi} \log \frac{|T'|}{2e} \pm \frac{B}{2\pi} \sum_{0\leq \ell\leq L} Q_{\ell}^{\pm} \left(\frac{B}{T},\frac{B}{T'} \right) \xi_0^{\ell+1}\bigg) \\&\quad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \ \cdot W_3^{\pm_1}\left( \frac{B} { \frac{NX}{PQ} },\frac{q}{P},\frac{yN}{T|T'|} \right) + O_A(T^{-A}). \end{align*} $$
Here, we take
![]() $L=L(A)$
to be large enough. This completes the proof of Lemma 4.2 (iii).
$L=L(A)$
to be large enough. This completes the proof of Lemma 4.2 (iii).
By (4.2), (4.3), and Lemma 4.2, we obtain
if
![]() $T^{\varepsilon } \ll \frac {NX}{PQ}\ll |T'|^{1-\varepsilon }$
, and
$T^{\varepsilon } \ll \frac {NX}{PQ}\ll |T'|^{1-\varepsilon }$
, and
 $$ \begin{align} S_{r}^{\pm}(N,X,P) \ll T^{\varepsilon} \sup_{M \ll \frac{P^2 T^2}{N} + \frac{NX^2}{Q^2} } |S_{r}^{\pm}(N,X,P,M)| + O(T^{-A}) \end{align} $$
$$ \begin{align} S_{r}^{\pm}(N,X,P) \ll T^{\varepsilon} \sup_{M \ll \frac{P^2 T^2}{N} + \frac{NX^2}{Q^2} } |S_{r}^{\pm}(N,X,P,M)| + O(T^{-A}) \end{align} $$
if
![]() $ \frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
, where
$ \frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
, where
 $$ \begin{align*} S_{r}^{\pm}(N,X,P,M) & : = X \frac{N^{1/2} }{Q}\sum_{\substack{q\sim P}} \;\frac{1}{q} U\left(\frac{q}{P}\right) \; \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} \frac{NX}{Q} \sum_{n_1|qr} \sum_{\substack{n_2=1 \\n_2 \asymp \frac{r N^{2}X^3} {n_1^2 Q^3} }}^{\infty} \frac{A(n_2,n_1)}{n_1n_2} S\left(-r\bar{a},\pm n_2;\frac{rq}{n_1}\right) \\&\quad\cdot V\left(\frac{ n_1^2n_2 Q^3}{r N^{2}X^3}\right) \sum_{\pm_1} \sum_{\substack{m\geq1 \\ m\asymp M}} \frac{ \lambda_{f}(m) }{m^{1/2}} \left(\frac{m}{q^2}\right)^{it} e\left(\frac{\pm_1\bar{a} m}{q}\right) W\left( \frac{m}{M}\right) \mathcal{I}^{\pm_1}(n_2,n_1,r,m,q) , \end{align*} $$
$$ \begin{align*} S_{r}^{\pm}(N,X,P,M) & : = X \frac{N^{1/2} }{Q}\sum_{\substack{q\sim P}} \;\frac{1}{q} U\left(\frac{q}{P}\right) \; \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} \frac{NX}{Q} \sum_{n_1|qr} \sum_{\substack{n_2=1 \\n_2 \asymp \frac{r N^{2}X^3} {n_1^2 Q^3} }}^{\infty} \frac{A(n_2,n_1)}{n_1n_2} S\left(-r\bar{a},\pm n_2;\frac{rq}{n_1}\right) \\&\quad\cdot V\left(\frac{ n_1^2n_2 Q^3}{r N^{2}X^3}\right) \sum_{\pm_1} \sum_{\substack{m\geq1 \\ m\asymp M}} \frac{ \lambda_{f}(m) }{m^{1/2}} \left(\frac{m}{q^2}\right)^{it} e\left(\frac{\pm_1\bar{a} m}{q}\right) W\left( \frac{m}{M}\right) \mathcal{I}^{\pm_1}(n_2,n_1,r,m,q) , \end{align*} $$
where
![]() $U,\; V,\; W$
are certain
$U,\; V,\; W$
are certain
![]() $T^{\varepsilon }$
-inert functions with compact support in
$T^{\varepsilon }$
-inert functions with compact support in
![]() $\mathbb {R}_{>0}$
and
$\mathbb {R}_{>0}$
and
 $$ \begin{align} \mathcal{I}^{\pm_1}(n_2,n_1,r,m,q) = e\left( \pm \frac{B}{2\pi} \sum_{0\leq \ell \leq L} Q_{\ell}^{\pm} \left(\frac{B}{T},\frac{B}{T'} \right) \xi_0^{\ell+1} \right) \end{align} $$
$$ \begin{align} \mathcal{I}^{\pm_1}(n_2,n_1,r,m,q) = e\left( \pm \frac{B}{2\pi} \sum_{0\leq \ell \leq L} Q_{\ell}^{\pm} \left(\frac{B}{T},\frac{B}{T'} \right) \xi_0^{\ell+1} \right) \end{align} $$
with
![]() $B=\frac { N^{1/3} ( n_1^2n_2)^{1/3} }{ r^{1/3} q} $
and
$B=\frac { N^{1/3} ( n_1^2n_2)^{1/3} }{ r^{1/3} q} $
and
![]() $\xi _0=\left (\frac {2\pi q^2 T|T'|}{mN}\right )^{1/3}$
if
$\xi _0=\left (\frac {2\pi q^2 T|T'|}{mN}\right )^{1/3}$
if
![]() $T^{\varepsilon } \ll \frac {NX}{PQ}\ll |T'|^{1-\varepsilon }$
, and
$T^{\varepsilon } \ll \frac {NX}{PQ}\ll |T'|^{1-\varepsilon }$
, and
 $$ \begin{align} \mathcal{I}^{\pm_1}(n_2,n_1,r,m,q) = \left( \frac{PQ}{NX}\right)^{1/2} \int_{\mathbb{R}} \left(\frac{ n_1^2n_2}{ mq} \right)^{i\tau} W_1\left(\frac{ n_1^2n_2 Q^3}{r N^{2}X^3}, \frac{\pm \tau} { \frac{NX}{PQ} } ,\frac{q}{P} \right) w^{\pm_1}(\tau) \mathrm{d} \tau \end{align} $$
$$ \begin{align} \mathcal{I}^{\pm_1}(n_2,n_1,r,m,q) = \left( \frac{PQ}{NX}\right)^{1/2} \int_{\mathbb{R}} \left(\frac{ n_1^2n_2}{ mq} \right)^{i\tau} W_1\left(\frac{ n_1^2n_2 Q^3}{r N^{2}X^3}, \frac{\pm \tau} { \frac{NX}{PQ} } ,\frac{q}{P} \right) w^{\pm_1}(\tau) \mathrm{d} \tau \end{align} $$
if
![]() $ \frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
. Here, we have used the Mellin technique to remove the weight function
$ \frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
. Here, we have used the Mellin technique to remove the weight function
![]() $W^{\pm _1}_3$
to get (4.11) without writing explicitly the dependence on those new parameters.
$W^{\pm _1}_3$
to get (4.11) without writing explicitly the dependence on those new parameters.
Changing the order of summations, we get
 $$ \begin{align} &S_{r}^{\pm}(N,X,P,M) = X \frac{N^{1/2} }{Q} \frac{NX}{Q} \sum_{n_1\ll Pr} \frac{1}{n_1} \sum_{\pm_1} \sum_{\substack{n_2=1 }}^{\infty} \frac{A(n_2,n_1)}{n_2} V\left(\frac{ n_1^2n_2 Q^3}{r N^{2}X^3}\right)\notag\\& \qquad \cdot\sum_{\substack{q\sim P \\ n_1\mid qr}} \;\frac{1}{q}U\left(\frac{q}{P}\right) \sum_{\substack{m\geq1 \\ m\asymp M }} \frac{ \lambda_{f}(m) }{m^{1/2}} \left(\frac{m}{q^2}\right)^{it} W\left(\frac{m}{M}\right) \mathcal{C}^{\pm_1}(n_2,n_1,r,m,q) \mathcal{I}^{\pm_1}(n_2,n_1,r,m,q) , \end{align} $$
$$ \begin{align} &S_{r}^{\pm}(N,X,P,M) = X \frac{N^{1/2} }{Q} \frac{NX}{Q} \sum_{n_1\ll Pr} \frac{1}{n_1} \sum_{\pm_1} \sum_{\substack{n_2=1 }}^{\infty} \frac{A(n_2,n_1)}{n_2} V\left(\frac{ n_1^2n_2 Q^3}{r N^{2}X^3}\right)\notag\\& \qquad \cdot\sum_{\substack{q\sim P \\ n_1\mid qr}} \;\frac{1}{q}U\left(\frac{q}{P}\right) \sum_{\substack{m\geq1 \\ m\asymp M }} \frac{ \lambda_{f}(m) }{m^{1/2}} \left(\frac{m}{q^2}\right)^{it} W\left(\frac{m}{M}\right) \mathcal{C}^{\pm_1}(n_2,n_1,r,m,q) \mathcal{I}^{\pm_1}(n_2,n_1,r,m,q) , \end{align} $$
where
 $$ \begin{align} \begin{aligned} \mathcal{C}^{\pm_1}(n_2,n_1,r,m,q) & := \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} e\left(\frac{\pm_1\bar{a} m}{q}\right) S\left(-r\bar{a},\pm n_2;\frac{rq}{n_1}\right) \\ & = \; \sideset{}{^{\star}}\sum_{\alpha \bmod rq/n_1} e\left(\frac{\pm n_2\bar\alpha}{rq/n_1}\right) \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} e\left(\frac{- n_1\bar{a} \alpha \pm_1\bar{a} m}{q}\right) \\ & = \sum_{d\mid q} d \mu\left(\frac{q}{d}\right) \; \sideset{}{^{\star}}\sum_{\substack{\alpha \bmod rq/n_1 \\ \pm_1 m \equiv n_1\alpha \bmod d}} e\left(\frac{\pm n_2 \bar\alpha}{rq/n_1}\right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathcal{C}^{\pm_1}(n_2,n_1,r,m,q) & := \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} e\left(\frac{\pm_1\bar{a} m}{q}\right) S\left(-r\bar{a},\pm n_2;\frac{rq}{n_1}\right) \\ & = \; \sideset{}{^{\star}}\sum_{\alpha \bmod rq/n_1} e\left(\frac{\pm n_2\bar\alpha}{rq/n_1}\right) \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} e\left(\frac{- n_1\bar{a} \alpha \pm_1\bar{a} m}{q}\right) \\ & = \sum_{d\mid q} d \mu\left(\frac{q}{d}\right) \; \sideset{}{^{\star}}\sum_{\substack{\alpha \bmod rq/n_1 \\ \pm_1 m \equiv n_1\alpha \bmod d}} e\left(\frac{\pm n_2 \bar\alpha}{rq/n_1}\right). \end{aligned} \end{align} $$
Here, we have used the following identity for the Ramanujan sum
 $$ \begin{align*} R_q(b) & = \;\sideset{}{^{\star}}\sum_{a\bmod{q}} e\left( \frac{b \overline{a}}{q} \right) = \sum_{d\mid (q,b)} d \mu\left(\frac{q}{d}\right). \end{align*} $$
$$ \begin{align*} R_q(b) & = \;\sideset{}{^{\star}}\sum_{a\bmod{q}} e\left( \frac{b \overline{a}}{q} \right) = \sum_{d\mid (q,b)} d \mu\left(\frac{q}{d}\right). \end{align*} $$
4.2 The nonoscillating case
If
![]() $\frac {NX}{PQ}\ll T^{\varepsilon }$
, then we have
$\frac {NX}{PQ}\ll T^{\varepsilon }$
, then we have
![]() $X\ll \frac {PQ} {N}T^{\varepsilon }$
and
$X\ll \frac {PQ} {N}T^{\varepsilon }$
and
 $$ \begin{align*} S_{r}^{\pm}(N,X,P) & = \frac{1}{Q}\sum_{\substack{q\sim P}} \int_{\mathbb{R}} V\left(\frac{\pm x}{X}\right) \; \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} \sum_{\pm} \sum_{n_1|qr} \sum_{n_2=1}^{\infty} \frac{A(n_2,n_1)}{n_1n_2} \\ & \cdot S\left(-r\bar{a},\pm n_2;\frac{rq}{n_1}\right) \Psi_x^{\pm}\left(\frac{n_1^2n_2}{q^3r}\right) \sum_{\substack{m\geq1}} \lambda_f(m) e\left(\frac{m a}{q}\right) e\left(\frac{m x}{qQ}\right) m^{-it} W\left(\frac{m}{N}\right) \mathrm{d}x. \end{align*} $$
$$ \begin{align*} S_{r}^{\pm}(N,X,P) & = \frac{1}{Q}\sum_{\substack{q\sim P}} \int_{\mathbb{R}} V\left(\frac{\pm x}{X}\right) \; \sideset{}{^{\star}}\sum_{\substack{a\bmod{q} }} \sum_{\pm} \sum_{n_1|qr} \sum_{n_2=1}^{\infty} \frac{A(n_2,n_1)}{n_1n_2} \\ & \cdot S\left(-r\bar{a},\pm n_2;\frac{rq}{n_1}\right) \Psi_x^{\pm}\left(\frac{n_1^2n_2}{q^3r}\right) \sum_{\substack{m\geq1}} \lambda_f(m) e\left(\frac{m a}{q}\right) e\left(\frac{m x}{qQ}\right) m^{-it} W\left(\frac{m}{N}\right) \mathrm{d}x. \end{align*} $$
We now apply the Voronoi summation formula (see Lemma 2.4) to the sum over m getting
 $$ \begin{align} \sum_{\substack{m\geq1}} \lambda_f(m) e\left(\frac{m a}{q}\right) e\left(\frac{m x}{qQ}\right) m^{-it} W\left(\frac{m}{N}\right) = q \sum_{\pm_1} \sum_{m\geq1} \frac{ \lambda_{f}(m) }{m} e\left(\frac{\pm_1\bar{a} m}{q}\right) G^{\pm_1} \left(\frac{m}{q^2} \right), \end{align} $$
$$ \begin{align} \sum_{\substack{m\geq1}} \lambda_f(m) e\left(\frac{m a}{q}\right) e\left(\frac{m x}{qQ}\right) m^{-it} W\left(\frac{m}{N}\right) = q \sum_{\pm_1} \sum_{m\geq1} \frac{ \lambda_{f}(m) }{m} e\left(\frac{\pm_1\bar{a} m}{q}\right) G^{\pm_1} \left(\frac{m}{q^2} \right), \end{align} $$
where
![]() $g(m)= e\left (\frac {m x}{qQ}\right ) m^{-it} W\left (\frac {m}{N}\right )$
and
$g(m)= e\left (\frac {m x}{qQ}\right ) m^{-it} W\left (\frac {m}{N}\right )$
and
![]() $G^{\pm _1}$
is defined as in (2.8).
$G^{\pm _1}$
is defined as in (2.8).
Lemma 4.3. Assume
![]() $x\asymp X$
and
$x\asymp X$
and
![]() $q\sim P$
. If
$q\sim P$
. If
![]() $\frac {NX}{PQ}\ll T^{\varepsilon }$
, then we have
$\frac {NX}{PQ}\ll T^{\varepsilon }$
, then we have
![]() $G^{\pm _1}(y)\ll y^{-6} T^{-A}$
, unless
$G^{\pm _1}(y)\ll y^{-6} T^{-A}$
, unless
![]() $yN\asymp T |T'|$
, in which case, we have
$yN\asymp T |T'|$
, in which case, we have
![]() $G^{\pm _1}(y) \ll T^{1/2+\varepsilon } |T'|^{1/2}$
.
$G^{\pm _1}(y) \ll T^{1/2+\varepsilon } |T'|^{1/2}$
.
Proof. We first consider the case
![]() $yN\gg T^{2+\varepsilon }$
. By the same argument as in the proof of Lemma 4.2 (i), we get
$yN\gg T^{2+\varepsilon }$
. By the same argument as in the proof of Lemma 4.2 (i), we get
![]() $G^{\pm _1}(y)\ll y^{-6} T^{-A}$
if
$G^{\pm _1}(y)\ll y^{-6} T^{-A}$
if
![]() $yN\gg T^{2+\varepsilon }$
.
$yN\gg T^{2+\varepsilon }$
.
Now, assume
![]() $yN\ll T^{2+\varepsilon }$
. As in the proof of Lemma 4.2, we have
$yN\ll T^{2+\varepsilon }$
. As in the proof of Lemma 4.2, we have
 $$ \begin{align*} G^{\pm_1}(y) = \frac{\epsilon_f^{(1\mp_1 1)/2}}{4\pi^2} \int_{\mathbb{R}} (\pi^2 y)^{1/2-i\tau+it} \gamma_2^{\pm_1}(-1/2+i\tau-it) \tilde{g}(1/2-i\tau+it) \mathrm{d} \tau. \end{align*} $$
$$ \begin{align*} G^{\pm_1}(y) = \frac{\epsilon_f^{(1\mp_1 1)/2}}{4\pi^2} \int_{\mathbb{R}} (\pi^2 y)^{1/2-i\tau+it} \gamma_2^{\pm_1}(-1/2+i\tau-it) \tilde{g}(1/2-i\tau+it) \mathrm{d} \tau. \end{align*} $$
If
![]() $\frac {NX}{PQ}\ll T^{\varepsilon }$
, then
$\frac {NX}{PQ}\ll T^{\varepsilon }$
, then
 $$ \begin{align*} \tilde{g}(1/2-i\tau+it) & = \int_{\mathbb{R}} e\left(\frac{u x}{qQ}\right) u^{-it} W\left(\frac{u}{N}\right) u^{1/2-i\tau+it-1} \mathrm{d} u \\ & = N^{1/2-i\tau} \int_{\mathbb{R}} e\left(\frac{Nx}{qQ} \xi- \frac{1}{2\pi} \tau \log \xi \right) W\left(\xi\right) \xi^{-1/2} \mathrm{d} \xi. \end{align*} $$
$$ \begin{align*} \tilde{g}(1/2-i\tau+it) & = \int_{\mathbb{R}} e\left(\frac{u x}{qQ}\right) u^{-it} W\left(\frac{u}{N}\right) u^{1/2-i\tau+it-1} \mathrm{d} u \\ & = N^{1/2-i\tau} \int_{\mathbb{R}} e\left(\frac{Nx}{qQ} \xi- \frac{1}{2\pi} \tau \log \xi \right) W\left(\xi\right) \xi^{-1/2} \mathrm{d} \xi. \end{align*} $$
By Lemma 2.7 with
we have
![]() $\tilde {g}(1/2-i\tau +it) \ll |\tau |^{-A}$
if
$\tilde {g}(1/2-i\tau +it) \ll |\tau |^{-A}$
if
![]() $|\tau |\gg T^{2\varepsilon }$
. By Stirling’s formula, we have
$|\tau |\gg T^{2\varepsilon }$
. By Stirling’s formula, we have
 $$ \begin{align*} G^{\pm_1}(y) &= (\pi^2 y)^{it} (Ny)^{1/2} \int_{\mathbb{R}} \int_{\mathbb{R}} (\pi^2 y N\xi)^{-i\tau} \exp\left( i(\tau - T)\log\frac{T-\tau}{2e} + i(\tau-T')\log\frac{|T'-\tau|}{2e} \right) \\&\qquad\cdot w_{\epsilon_f,J}^{\pm_1}(\tau-T) w_{\epsilon_f,J}^{\pm_1}(\tau-T') U\left( \frac{\tau}{T^{2\varepsilon}} \right) \mathrm{d} \tau \; e\left(\frac{Nx}{qQ} \xi\right) W\left(\xi\right) \xi^{-1/2} \mathrm{d} \xi + O(T^{-A}), \end{align*} $$
$$ \begin{align*} G^{\pm_1}(y) &= (\pi^2 y)^{it} (Ny)^{1/2} \int_{\mathbb{R}} \int_{\mathbb{R}} (\pi^2 y N\xi)^{-i\tau} \exp\left( i(\tau - T)\log\frac{T-\tau}{2e} + i(\tau-T')\log\frac{|T'-\tau|}{2e} \right) \\&\qquad\cdot w_{\epsilon_f,J}^{\pm_1}(\tau-T) w_{\epsilon_f,J}^{\pm_1}(\tau-T') U\left( \frac{\tau}{T^{2\varepsilon}} \right) \mathrm{d} \tau \; e\left(\frac{Nx}{qQ} \xi\right) W\left(\xi\right) \xi^{-1/2} \mathrm{d} \xi + O(T^{-A}), \end{align*} $$
where U is a fixed compactly supported smooth function satisfying that
![]() $U^{(j)}(u) \ll _j 1$
for all
$U^{(j)}(u) \ll _j 1$
for all
![]() $j\geq 0$
, and
$j\geq 0$
, and
![]() $U(u)=1$
if
$U(u)=1$
if
![]() $u\in [-1,1]$
. Let (temporarily)
$u\in [-1,1]$
. Let (temporarily)
Then, we have
 $$\begin{align*}h'(\tau) &= - \log (\pi^2 y N\xi) + \log\frac{T-\tau}{2} + \log\frac{|T'-\tau|}{2} ,\\h"(\tau) &= \frac {-1}{T-\tau} - \frac{1} {T'-\tau} , \quad h^{(j)}(\tau) \ll |T'|^{-j+1}, \quad j\geq2. \end{align*}$$
$$\begin{align*}h'(\tau) &= - \log (\pi^2 y N\xi) + \log\frac{T-\tau}{2} + \log\frac{|T'-\tau|}{2} ,\\h"(\tau) &= \frac {-1}{T-\tau} - \frac{1} {T'-\tau} , \quad h^{(j)}(\tau) \ll |T'|^{-j+1}, \quad j\geq2. \end{align*}$$
Note that the weight function
![]() $w(\tau ) = w_{\epsilon _f,J}^{\pm _1}(\tau -T) w_{\epsilon _f,J}^{\pm _1}(\tau -T') U\left ( \frac {\tau }{T^{2\varepsilon }} \right )$
satisfies that
$w(\tau ) = w_{\epsilon _f,J}^{\pm _1}(\tau -T) w_{\epsilon _f,J}^{\pm _1}(\tau -T') U\left ( \frac {\tau }{T^{2\varepsilon }} \right )$
satisfies that
![]() $w^{(j)}(\tau ) \ll T^{-2j\varepsilon }$
. By Lemma 2.7 with
$w^{(j)}(\tau ) \ll T^{-2j\varepsilon }$
. By Lemma 2.7 with
we have
![]() $G^{\pm _1}(y) \ll T^{-A}$
, unless
$G^{\pm _1}(y) \ll T^{-A}$
, unless
![]() $yN\asymp T |T'|$
, in which case, we have
$yN\asymp T |T'|$
, in which case, we have
![]() $G^{\pm _1}(y) \ll (yN)^{1/2} T^{\varepsilon } \ll T^{1/2+\varepsilon }|T'|^{1/2}$
.
$G^{\pm _1}(y) \ll (yN)^{1/2} T^{\varepsilon } \ll T^{1/2+\varepsilon }|T'|^{1/2}$
.
 $$ \begin{align*} S_{r}^{\pm}(N,X,P) & =\frac{1}{Q}\sum_{\substack{q\sim P}} \int_{\mathbb{R}} V\left(\frac{\pm x}{X}\right) \; \sum_{\pm} \sum_{n_1|qr} \sum_{n_2=1}^{\infty} \frac{A(n_2,n_1)}{n_1n_2} \Psi_x^{\pm}\left(\frac{n_1^2n_2}{q^3r}\right)\\ & \hskip 60pt \cdot q \sum_{\pm_1} \sum_{m\geq1} \frac{ \lambda_{f}(m) }{m} \mathcal{C}^{\pm_1}(n_2,n_1,r,m,q) G^{\pm_1} \left(\frac{m}{q^2} \right) \mathrm{d}x , \end{align*} $$
$$ \begin{align*} S_{r}^{\pm}(N,X,P) & =\frac{1}{Q}\sum_{\substack{q\sim P}} \int_{\mathbb{R}} V\left(\frac{\pm x}{X}\right) \; \sum_{\pm} \sum_{n_1|qr} \sum_{n_2=1}^{\infty} \frac{A(n_2,n_1)}{n_1n_2} \Psi_x^{\pm}\left(\frac{n_1^2n_2}{q^3r}\right)\\ & \hskip 60pt \cdot q \sum_{\pm_1} \sum_{m\geq1} \frac{ \lambda_{f}(m) }{m} \mathcal{C}^{\pm_1}(n_2,n_1,r,m,q) G^{\pm_1} \left(\frac{m}{q^2} \right) \mathrm{d}x , \end{align*} $$
where
![]() $\mathcal {C}^{\pm _1}(n_2,n_1,r,m,q)$
is defined in (4.14). Note that we have
$\mathcal {C}^{\pm _1}(n_2,n_1,r,m,q)$
is defined in (4.14). Note that we have
 $$\begin{align*}\mathcal{C}^{\pm_1}(n_2,n_1,r,m,q) \ll \sum_{d\mid q} d \; \sideset{}{^{\star}}\sum_{\substack{\alpha \bmod rq/n_1 \\ \pm_1 m \equiv n_1\alpha \bmod d}} 1 \ll rq^{1+\varepsilon}. \end{align*}$$
$$\begin{align*}\mathcal{C}^{\pm_1}(n_2,n_1,r,m,q) \ll \sum_{d\mid q} d \; \sideset{}{^{\star}}\sum_{\substack{\alpha \bmod rq/n_1 \\ \pm_1 m \equiv n_1\alpha \bmod d}} 1 \ll rq^{1+\varepsilon}. \end{align*}$$
By Lemmas 4.1 and 4.3, we obtain
 $$ \begin{align*} S_{r}^{\pm}(N,X,P) & \ll \frac{N^{\varepsilon}}{Q}\sum_{\substack{q\sim P}} rq X \sum_{n_1|qr} \frac{1}{n_1} \!\sum_{n_2 \ll \frac{rP^3}{Nn_1^2}T^{\varepsilon}} \frac{|A(n_2,n_1)|}{n_2} q\\& \quad \times \sum_{m\asymp \frac{P^2 T |T'|}{N}} \frac{ |\lambda_{f}(m)| }{m} T^{1/2} |T'|^{1/2} + O(T^{-A}). \end{align*} $$
$$ \begin{align*} S_{r}^{\pm}(N,X,P) & \ll \frac{N^{\varepsilon}}{Q}\sum_{\substack{q\sim P}} rq X \sum_{n_1|qr} \frac{1}{n_1} \!\sum_{n_2 \ll \frac{rP^3}{Nn_1^2}T^{\varepsilon}} \frac{|A(n_2,n_1)|}{n_2} q\\& \quad \times \sum_{m\asymp \frac{P^2 T |T'|}{N}} \frac{ |\lambda_{f}(m)| }{m} T^{1/2} |T'|^{1/2} + O(T^{-A}). \end{align*} $$
 $$ \begin{align*} S_{r}^{\pm}(N,X,P) & \ll N^{\varepsilon} \frac{1}{Q}\sum_{\substack{q\sim P}} rq X \sum_{n_1|qr} \frac{1}{n_1} n_1^{\theta_3 } q T^{1/2} |T'|^{1/2} + O(T^{-A}) \nonumber \\ & \ll N^{\varepsilon} \frac{rP^3 XT^{1/2} |T'|^{1/2}}{Q} + O(T^{-A}). \end{align*} $$
$$ \begin{align*} S_{r}^{\pm}(N,X,P) & \ll N^{\varepsilon} \frac{1}{Q}\sum_{\substack{q\sim P}} rq X \sum_{n_1|qr} \frac{1}{n_1} n_1^{\theta_3 } q T^{1/2} |T'|^{1/2} + O(T^{-A}) \nonumber \\ & \ll N^{\varepsilon} \frac{rP^3 XT^{1/2} |T'|^{1/2}}{Q} + O(T^{-A}). \end{align*} $$
Note that by our assumption, we have
![]() $X\ll \frac {PQ} {N}T^{\varepsilon }$
. Hence, we get
$X\ll \frac {PQ} {N}T^{\varepsilon }$
. Hence, we get
 $$ \begin{align} S_{r}^{\pm}(N,X,P) & \ll N^{\varepsilon} \frac{rP^3 PQ T^{1/2} |T'|^{1/2}}{QN} \ll N^{\varepsilon} \frac{r Q^4 T^{1/2} |T'|^{1/2}}{N} \nonumber \\ & \ll N^{1/2+\varepsilon} \left(T^{7/8} |T'|^{19/40} + T^{57/56} |T'|^{17/56} \right), \end{align} $$
$$ \begin{align} S_{r}^{\pm}(N,X,P) & \ll N^{\varepsilon} \frac{rP^3 PQ T^{1/2} |T'|^{1/2}}{QN} \ll N^{\varepsilon} \frac{r Q^4 T^{1/2} |T'|^{1/2}}{N} \nonumber \\ & \ll N^{1/2+\varepsilon} \left(T^{7/8} |T'|^{19/40} + T^{57/56} |T'|^{17/56} \right), \end{align} $$
provided
![]() $N\ll \frac {T^{3/2+\varepsilon }|T'|^{3/2}}{r^2}$
and
$N\ll \frac {T^{3/2+\varepsilon }|T'|^{3/2}}{r^2}$
and
![]() $Q=\sqrt {\frac {N}{K}}$
with
$Q=\sqrt {\frac {N}{K}}$
with
 $$ \begin{align} K\geq \left\{ \begin{array}{ll} T^{3/16}|T'|^{31/80}, & \textrm{if } T'\gg T^{5/6}, \\ T^{13/112}|T'|^{53/112}, & \textrm{if } T^{3/5+\varepsilon} \ll T'\ll T^{5/6}. \end{array} \right. \end{align} $$
$$ \begin{align} K\geq \left\{ \begin{array}{ll} T^{3/16}|T'|^{31/80}, & \textrm{if } T'\gg T^{5/6}, \\ T^{13/112}|T'|^{53/112}, & \textrm{if } T^{3/5+\varepsilon} \ll T'\ll T^{5/6}. \end{array} \right. \end{align} $$
5 Applying Cauchy and Poisson
Assume
![]() $\frac {NX}{PQ}\gg T^{\varepsilon }$
. Write
$\frac {NX}{PQ}\gg T^{\varepsilon }$
. Write
![]() $q=q_1q_2$
with
$q=q_1q_2$
with
![]() $\frac {n_1}{(n_1,r)}\mid q_1 \mid (n_1r)^{\infty }$
and
$\frac {n_1}{(n_1,r)}\mid q_1 \mid (n_1r)^{\infty }$
and
![]() $(q_2,n_1r)=1$
. By (4.13), we have
$(q_2,n_1r)=1$
. By (4.13), we have
 $$ \begin{align*} &S_{r}^{\pm}(N,X,P,M) = \frac{ Q }{r N^{1/2} P X M^{1/2}} \sum_{\pm_1} \sum_{n_1\ll Pr} n_1 \sum_{\substack{n_2=1 }}^{\infty} A(n_2,n_1) V\left(\frac{ n_1^2n_2 Q^3}{r N^{2}X^3}\right) \frac{r N^{2}X^3}{ n_1^2n_2 Q^3} \sum_{\frac{n_1}{(n_1,r)}\mid q_1 \mid (n_1r)^{\infty}} \\&\quad \cdot \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} \;\frac{P}{q}U\left(\frac{q}{P}\right)q^{-2it} \sum_{\substack{m\geq1 \\ m\asymp M }} \frac{ \lambda_{f}(m) M^{1/2}}{m^{1/2}} m^{it} W\left(\frac{m}{M}\right) \mathcal{C}^{\pm_1}(n_2,n_1,r,m,q) \mathcal{I}^{\pm_1}(n_2,n_1,r,m,q). \end{align*} $$
$$ \begin{align*} &S_{r}^{\pm}(N,X,P,M) = \frac{ Q }{r N^{1/2} P X M^{1/2}} \sum_{\pm_1} \sum_{n_1\ll Pr} n_1 \sum_{\substack{n_2=1 }}^{\infty} A(n_2,n_1) V\left(\frac{ n_1^2n_2 Q^3}{r N^{2}X^3}\right) \frac{r N^{2}X^3}{ n_1^2n_2 Q^3} \sum_{\frac{n_1}{(n_1,r)}\mid q_1 \mid (n_1r)^{\infty}} \\&\quad \cdot \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} \;\frac{P}{q}U\left(\frac{q}{P}\right)q^{-2it} \sum_{\substack{m\geq1 \\ m\asymp M }} \frac{ \lambda_{f}(m) M^{1/2}}{m^{1/2}} m^{it} W\left(\frac{m}{M}\right) \mathcal{C}^{\pm_1}(n_2,n_1,r,m,q) \mathcal{I}^{\pm_1}(n_2,n_1,r,m,q). \end{align*} $$
Since the cases
![]() $\pm _1=+$
and
$\pm _1=+$
and
![]() $\pm _1=-$
can be estimated in the same way, we do not write down
$\pm _1=-$
can be estimated in the same way, we do not write down
![]() $\pm _1$
explicitly from now on. Hence, we have
$\pm _1$
explicitly from now on. Hence, we have
 $$ \begin{align*} S_{r}^{\pm}(N,X,P,M) \kern1.2pt{\ll}\kern1.2pt \frac{ Q }{r N^{1/2} P X M^{1/2}} \sum_{n_1\ll Pr}\!\! n_1 \!\!\sum_{\frac{n_1}{(n_1,r)}\mid q_1 \mid (n_1r)^{\infty}} \!\!\sum_{\substack{n_2\geq 1 \\n_2 \asymp \frac{r N^{2}X^3} {n_1^2 Q^3} }} \!\!\kern-1pt|A(n_2,n_1)| |\mathcal B(n_2,n_1,q_1)| , \end{align*} $$
$$ \begin{align*} S_{r}^{\pm}(N,X,P,M) \kern1.2pt{\ll}\kern1.2pt \frac{ Q }{r N^{1/2} P X M^{1/2}} \sum_{n_1\ll Pr}\!\! n_1 \!\!\sum_{\frac{n_1}{(n_1,r)}\mid q_1 \mid (n_1r)^{\infty}} \!\!\sum_{\substack{n_2\geq 1 \\n_2 \asymp \frac{r N^{2}X^3} {n_1^2 Q^3} }} \!\!\kern-1pt|A(n_2,n_1)| |\mathcal B(n_2,n_1,q_1)| , \end{align*} $$
where
 $$ \begin{align*} \mathcal B(n_2,n_1,q_1) = \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} b_{q_2} \sum_{\substack{ m\asymp M}} c_m \; \mathcal{C}(n_2,n_1,r,m,q_1q_2) \mathcal{I}(n_2,n_1,r,m,q_1q_2) \end{align*} $$
$$ \begin{align*} \mathcal B(n_2,n_1,q_1) = \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} b_{q_2} \sum_{\substack{ m\asymp M}} c_m \; \mathcal{C}(n_2,n_1,r,m,q_1q_2) \mathcal{I}(n_2,n_1,r,m,q_1q_2) \end{align*} $$
with
![]() $b_{q_2}=\frac {P}{q_1q_2}U\left (\frac {q_1q_2}{P}\right )(q_1q_2)^{-2it}$
and
$b_{q_2}=\frac {P}{q_1q_2}U\left (\frac {q_1q_2}{P}\right )(q_1q_2)^{-2it}$
and
![]() $c_m=\frac { \lambda _{f}(m) M^{1/2}}{m^{1/2}} m^{it} W\left (\frac {m}{M}\right )$
, such that
$c_m=\frac { \lambda _{f}(m) M^{1/2}}{m^{1/2}} m^{it} W\left (\frac {m}{M}\right )$
, such that
Here, we have used (2.1) for the m-sum. By the Cauchy–Schwarz inequality, we get
 $$ \begin{align*} &S_{r}^{\pm}(N,X,P,M) \ll \frac{ Q }{r N^{1/2} P X M^{1/2}} \sum_{n_1}\! \left(\sum_{\substack{n_2}} |A(n_2,n_1)|^2 \right)^{\kern-3pt 1/2} n_1\! \sum_{q_1} \left(\sum_{\substack{n_2}}|\mathcal B(n_2,n_1,q_1)|^2\right)^{\kern-3pt 1/2} \\ &\quad\ll \frac{ Q }{r N^{1/2} P X M^{1/2}} \sum_{n_1} \!\left(\sum_{\substack{n_2}} |A(n_2,n_1)|^2 \right)^{\kern-3pt 1/2} n_1 \left(\sum_{q_1}1\right)^{\kern-3pt 1/2} \left(\sum_{q_1} \sum_{\substack{n_2}}|\mathcal B(n_2,n_1,q_1)|^2\right)^{\kern-3pt 1/2}\!. \end{align*} $$
$$ \begin{align*} &S_{r}^{\pm}(N,X,P,M) \ll \frac{ Q }{r N^{1/2} P X M^{1/2}} \sum_{n_1}\! \left(\sum_{\substack{n_2}} |A(n_2,n_1)|^2 \right)^{\kern-3pt 1/2} n_1\! \sum_{q_1} \left(\sum_{\substack{n_2}}|\mathcal B(n_2,n_1,q_1)|^2\right)^{\kern-3pt 1/2} \\ &\quad\ll \frac{ Q }{r N^{1/2} P X M^{1/2}} \sum_{n_1} \!\left(\sum_{\substack{n_2}} |A(n_2,n_1)|^2 \right)^{\kern-3pt 1/2} n_1 \left(\sum_{q_1}1\right)^{\kern-3pt 1/2} \left(\sum_{q_1} \sum_{\substack{n_2}}|\mathcal B(n_2,n_1,q_1)|^2\right)^{\kern-3pt 1/2}\!. \end{align*} $$
Note that we have
 $$\begin{align*}\sum_{q_1}\!1 \kern1.2pt{\leq}\kern1.2pt \sum_{\substack{\frac{n_1}{(n_1,r)}\mid q_1 \mid (n_1r)^{\infty} \\ q_1\ll P}} 1 \kern1.2pt{\ll}\kern1.2pt P^{\varepsilon} \!\sum_{q_1 \mid (n_1r)^{\infty}} q_1^{-\varepsilon} \kern1.2pt{=}\kern1.2ptP^{\varepsilon} \prod_{p \mid n_1r} \sum_{k=1}^{\infty} p^{-k\varepsilon} \kern1.2pt{\ll}\kern1.2pt P^{\varepsilon} \exp\!\!\kern-1pt\left(\sum_{p \mid n_1r} \!O(p^{-\varepsilon}) \kern-3pt\right) \!\!\ll N^{\varepsilon}\!. \end{align*}$$
$$\begin{align*}\sum_{q_1}\!1 \kern1.2pt{\leq}\kern1.2pt \sum_{\substack{\frac{n_1}{(n_1,r)}\mid q_1 \mid (n_1r)^{\infty} \\ q_1\ll P}} 1 \kern1.2pt{\ll}\kern1.2pt P^{\varepsilon} \!\sum_{q_1 \mid (n_1r)^{\infty}} q_1^{-\varepsilon} \kern1.2pt{=}\kern1.2ptP^{\varepsilon} \prod_{p \mid n_1r} \sum_{k=1}^{\infty} p^{-k\varepsilon} \kern1.2pt{\ll}\kern1.2pt P^{\varepsilon} \exp\!\!\kern-1pt\left(\sum_{p \mid n_1r} \!O(p^{-\varepsilon}) \kern-3pt\right) \!\!\ll N^{\varepsilon}\!. \end{align*}$$
Here, we have used
![]() $\sum _{p \mid n_1r} O(p^{-\varepsilon })=O(\omega (n_1r))=o(\log n_1r)+O(1) = o(\log N)$
. Hence, we have
$\sum _{p \mid n_1r} O(p^{-\varepsilon })=O(\omega (n_1r))=o(\log n_1r)+O(1) = o(\log N)$
. Hence, we have
 $$ \begin{align} S_{r}^{\pm}(N,X,P,M) &\ll \frac{ N^{\varepsilon} Q }{r N^{1/2} P X M^{1/2}} \left(\sum_{n_1}\sum_{\substack{n_2}} |A(n_2,n_1)|^2 \right)^{\!1/2} \left( \sum_{n_1} n_1^2 \sum_{q_1} \sum_{\substack{n_2}}|B(n_2,n_1,q_1)|^2 \right)^{\!1/2} \notag \\ &\qquad\qquad\ll \frac{ N^{\varepsilon} Q }{r N^{1/2} P X M^{1/2}} \left(\frac{r N^{2}X^3} {Q^3} \right)^{1/2} \left(\sum_{n_1\ll Pr} n_1^2 \sum_{\frac{n_1}{(n_1,r)}\mid q_1 \mid (n_1r)^{\infty}} \Omega_{\pm} \right)^{1/2} , \hskip 30pt \end{align} $$
$$ \begin{align} S_{r}^{\pm}(N,X,P,M) &\ll \frac{ N^{\varepsilon} Q }{r N^{1/2} P X M^{1/2}} \left(\sum_{n_1}\sum_{\substack{n_2}} |A(n_2,n_1)|^2 \right)^{\!1/2} \left( \sum_{n_1} n_1^2 \sum_{q_1} \sum_{\substack{n_2}}|B(n_2,n_1,q_1)|^2 \right)^{\!1/2} \notag \\ &\qquad\qquad\ll \frac{ N^{\varepsilon} Q }{r N^{1/2} P X M^{1/2}} \left(\frac{r N^{2}X^3} {Q^3} \right)^{1/2} \left(\sum_{n_1\ll Pr} n_1^2 \sum_{\frac{n_1}{(n_1,r)}\mid q_1 \mid (n_1r)^{\infty}} \Omega_{\pm} \right)^{1/2} , \hskip 30pt \end{align} $$
where
 $$ \begin{align*} \Omega_{\pm} = \sum_{\substack{n_2\geq1}} W\left(\frac{n_2}{N_2}\right) \bigg| \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} b_{q_2} \sum_{\substack{m\geq1 \\ m\asymp M}} c_m \; \mathcal{C}(n_2,n_1,r,m,q_1q_2) \mathcal{I}(n_2,n_1,r,m,q_1q_2) \bigg|^2, \end{align*} $$
$$ \begin{align*} \Omega_{\pm} = \sum_{\substack{n_2\geq1}} W\left(\frac{n_2}{N_2}\right) \bigg| \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} b_{q_2} \sum_{\substack{m\geq1 \\ m\asymp M}} c_m \; \mathcal{C}(n_2,n_1,r,m,q_1q_2) \mathcal{I}(n_2,n_1,r,m,q_1q_2) \bigg|^2, \end{align*} $$
where
![]() $N_2 = \frac {r N^{2}X^3} {n_1^2 Q^3} $
and W is a
$N_2 = \frac {r N^{2}X^3} {n_1^2 Q^3} $
and W is a
![]() $1$
-inert function with compact support in
$1$
-inert function with compact support in
![]() $\mathbb {R}_{>0}$
. Opening the square and rearranging the sums, we get
$\mathbb {R}_{>0}$
. Opening the square and rearranging the sums, we get
 $$ \begin{align*} &\Omega_{\pm} = \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} b_{q_2} \sum_{\substack{m\geq1 \\ m\asymp M}} c_m \sum_{\substack{q_2^{\prime}\sim P/q_1 \\ (q_2^{\prime},n_1r)=1}} \overline{ b_{q_2^{\prime}} } \sum_{\substack{m'\geq1 \\ m'\asymp M}} \overline{c_{m'}} \sum_{\substack{n_2\geq1}} W\left(\frac{n_2}{N_2}\right) \\ &\qquad\qquad\cdot \; \mathcal{C}(n_2,n_1,r,m,q_1q_2) \overline{\mathcal{C}(n_2,n_1,r,m',q_1q_2^{\prime})} \; \mathcal{I}(n_2,n_1,r,m,q_1q_2) \overline{\mathcal{I}(n_2,n_1,r,m',q_1q_2^{\prime})}. \end{align*} $$
$$ \begin{align*} &\Omega_{\pm} = \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} b_{q_2} \sum_{\substack{m\geq1 \\ m\asymp M}} c_m \sum_{\substack{q_2^{\prime}\sim P/q_1 \\ (q_2^{\prime},n_1r)=1}} \overline{ b_{q_2^{\prime}} } \sum_{\substack{m'\geq1 \\ m'\asymp M}} \overline{c_{m'}} \sum_{\substack{n_2\geq1}} W\left(\frac{n_2}{N_2}\right) \\ &\qquad\qquad\cdot \; \mathcal{C}(n_2,n_1,r,m,q_1q_2) \overline{\mathcal{C}(n_2,n_1,r,m',q_1q_2^{\prime})} \; \mathcal{I}(n_2,n_1,r,m,q_1q_2) \overline{\mathcal{I}(n_2,n_1,r,m',q_1q_2^{\prime})}. \end{align*} $$
Applying Poisson summation on the sum over
![]() $n_2$
modulo
$n_2$
modulo
![]() $ rq_1 q_2q_2^{\prime }/n_1 $
(Lemma 2.3), we arrive at
$ rq_1 q_2q_2^{\prime }/n_1 $
(Lemma 2.3), we arrive at
 $$ \begin{align} \Omega_{\pm} = \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} b_{q_2} \sum_{\substack{m\geq1 \\ m\asymp M}} c_m \sum_{\substack{q_2^{\prime}\sim P/q_1 \\ (q_2^{\prime},n_1r)=1}} \overline{ b_{q_2^{\prime}} } \sum_{\substack{m'\geq1 \\ m'\asymp M}} \overline{c_{m'}} \sum_{\substack{n\in \mathbb{Z}}} \mathfrak{C}(n) \mathfrak{I}(n), \end{align} $$
$$ \begin{align} \Omega_{\pm} = \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} b_{q_2} \sum_{\substack{m\geq1 \\ m\asymp M}} c_m \sum_{\substack{q_2^{\prime}\sim P/q_1 \\ (q_2^{\prime},n_1r)=1}} \overline{ b_{q_2^{\prime}} } \sum_{\substack{m'\geq1 \\ m'\asymp M}} \overline{c_{m'}} \sum_{\substack{n\in \mathbb{Z}}} \mathfrak{C}(n) \mathfrak{I}(n), \end{align} $$
where
 $$ \begin{align*} \mathfrak{C}(n) & = \frac{1}{rq_1 q_2q_2^{\prime}/n_1} \sum_{\beta(rq_1 q_2q_2^{\prime}/n_1)} \mathcal{C}(\beta,n_1,r,m,q_1q_2) \overline{\mathcal{C}(\beta,n_1,r,m',q_1q_2^{\prime})} e\left( \frac{n\beta}{rq_1 q_2q_2^{\prime}/n_1}\right) \\ & = \sum_{d\mid q} d \mu\left(\frac{q}{d}\right) \sum_{d'\mid q'} d' \mu\left(\frac{q'}{d'}\right)\; \mathop{ \sideset{}{^{\star}}\sum_{\substack{\alpha \bmod rq/n_1 \\ \pm_1 m \equiv n_1\alpha \bmod d}} \; \sideset{}{^{\star}}\sum_{\substack{\alpha' \bmod rq'/n_1 \\ \pm_1 m' \equiv n_1\alpha' \bmod d'}} }_{ \pm q_2^{\prime} \bar\alpha \mp q_2 \bar\alpha' \equiv -n \bmod rq_1 q_2q_2^{\prime}/n_1 } 1 \end{align*} $$
$$ \begin{align*} \mathfrak{C}(n) & = \frac{1}{rq_1 q_2q_2^{\prime}/n_1} \sum_{\beta(rq_1 q_2q_2^{\prime}/n_1)} \mathcal{C}(\beta,n_1,r,m,q_1q_2) \overline{\mathcal{C}(\beta,n_1,r,m',q_1q_2^{\prime})} e\left( \frac{n\beta}{rq_1 q_2q_2^{\prime}/n_1}\right) \\ & = \sum_{d\mid q} d \mu\left(\frac{q}{d}\right) \sum_{d'\mid q'} d' \mu\left(\frac{q'}{d'}\right)\; \mathop{ \sideset{}{^{\star}}\sum_{\substack{\alpha \bmod rq/n_1 \\ \pm_1 m \equiv n_1\alpha \bmod d}} \; \sideset{}{^{\star}}\sum_{\substack{\alpha' \bmod rq'/n_1 \\ \pm_1 m' \equiv n_1\alpha' \bmod d'}} }_{ \pm q_2^{\prime} \bar\alpha \mp q_2 \bar\alpha' \equiv -n \bmod rq_1 q_2q_2^{\prime}/n_1 } 1 \end{align*} $$
and
 $$ \begin{align} \mathfrak{I}(n) &= \int_{\mathbb{R}} W\left(\frac{u}{N_2}\right) \; \mathcal{I}(u,n_1,r,m,q_1q_2) \overline{\mathcal{I}(u,n_1,r,m',q_1q_2^{\prime})} e\left(\frac{-nu}{rq_1 q_2q_2^{\prime}/n_1} \right) \mathrm{d} u \nonumber \\ &= N_2 \int_{\mathbb{R}} W\left(\xi\right) \; \mathcal{I}(N_2\xi,n_1,r,m,q_1q_2) \overline{\mathcal{I}(N_2\xi,n_1,r,m',q_1q_2^{\prime})} e\left(\frac{-nN_2 \xi}{rq_1 q_2q_2^{\prime}/n_1} \right) \mathrm{d} \xi. \end{align} $$
$$ \begin{align} \mathfrak{I}(n) &= \int_{\mathbb{R}} W\left(\frac{u}{N_2}\right) \; \mathcal{I}(u,n_1,r,m,q_1q_2) \overline{\mathcal{I}(u,n_1,r,m',q_1q_2^{\prime})} e\left(\frac{-nu}{rq_1 q_2q_2^{\prime}/n_1} \right) \mathrm{d} u \nonumber \\ &= N_2 \int_{\mathbb{R}} W\left(\xi\right) \; \mathcal{I}(N_2\xi,n_1,r,m,q_1q_2) \overline{\mathcal{I}(N_2\xi,n_1,r,m',q_1q_2^{\prime})} e\left(\frac{-nN_2 \xi}{rq_1 q_2q_2^{\prime}/n_1} \right) \mathrm{d} \xi. \end{align} $$
The following lemma on the character sums is essentially due to Munshi [Reference Munshi40] and is actually the same as the results in Huang–Xu [Reference Huang and Xu19].
Lemma 5.1. We have
![]() $\mathfrak {C}(0)=0$
, unless
$\mathfrak {C}(0)=0$
, unless
in which case, we have
 $$\begin{align*}\mathfrak{C}(0) \ll \mathop{\sum_{d\mid q} \sum_{d'\mid q}}_{(d,d')\mid (m-m')} (d,d') qr. \end{align*}$$
$$\begin{align*}\mathfrak{C}(0) \ll \mathop{\sum_{d\mid q} \sum_{d'\mid q}}_{(d,d')\mid (m-m')} (d,d') qr. \end{align*}$$
If
![]() $n\neq 0$
, then we have
$n\neq 0$
, then we have
 $$ \begin{align*} &\mathfrak{C}(n) \ll \frac{rq_1}{n_1} \sum_{d_1\mid q_1} \sum_{d_1^{\prime}\mid q_1} \min \left\{ d_1^{\prime} (d_1,n_1) \delta_{(d_1,n_1)\mid m}, d_1 (d_1^{\prime},n_1) \delta_{(d_1^{\prime},n_1)\mid m'} \right\} \\ &\qquad\qquad\cdot \mathop{\sum\sum}_{\substack{d_2 \mid (q_2, \pm n_1 q_2^{\prime}\pm_1 mn) \\ d_2^{\prime} \mid (q_2^{\prime}, \mp n_1 q_2 \pm_1 m'n)}} d_2d_2^{\prime} \; \min\left\{\frac{q_2}{[q_2/(q_2,q_2^{\prime}),d_2]},\frac{q_2^{\prime}}{[q_2^{\prime}/(q_2,q_2^{\prime}),d_2^{\prime}]} \right\} \; \delta_{(q_2,q_2^{\prime})\mid n}. \end{align*} $$
$$ \begin{align*} &\mathfrak{C}(n) \ll \frac{rq_1}{n_1} \sum_{d_1\mid q_1} \sum_{d_1^{\prime}\mid q_1} \min \left\{ d_1^{\prime} (d_1,n_1) \delta_{(d_1,n_1)\mid m}, d_1 (d_1^{\prime},n_1) \delta_{(d_1^{\prime},n_1)\mid m'} \right\} \\ &\qquad\qquad\cdot \mathop{\sum\sum}_{\substack{d_2 \mid (q_2, \pm n_1 q_2^{\prime}\pm_1 mn) \\ d_2^{\prime} \mid (q_2^{\prime}, \mp n_1 q_2 \pm_1 m'n)}} d_2d_2^{\prime} \; \min\left\{\frac{q_2}{[q_2/(q_2,q_2^{\prime}),d_2]},\frac{q_2^{\prime}}{[q_2^{\prime}/(q_2,q_2^{\prime}),d_2^{\prime}]} \right\} \; \delta_{(q_2,q_2^{\prime})\mid n}. \end{align*} $$
Here,
![]() $\delta _{(d_1,n_1)\mid m}=1$
if
$\delta _{(d_1,n_1)\mid m}=1$
if
![]() $(d_1,n_1)\mid m$
holds, otherwise we have
$(d_1,n_1)\mid m$
holds, otherwise we have
![]() $\delta _{(d_1,n_1)\mid m}=0$
.
$\delta _{(d_1,n_1)\mid m}=0$
.
Proof. If
![]() $n=0$
, then
$n=0$
, then
![]() $ \pm q_2^{\prime } \bar \alpha \mp q_2 \bar \alpha ' \equiv 0 \bmod rq_1 q_2q_2^{\prime }/n_1$
. Since
$ \pm q_2^{\prime } \bar \alpha \mp q_2 \bar \alpha ' \equiv 0 \bmod rq_1 q_2q_2^{\prime }/n_1$
. Since
![]() $(\alpha ,rq_1 q_2/n_1)=(\alpha ',rq_1 q_2^{\prime }/ n_1)=1$
, we have
$(\alpha ,rq_1 q_2/n_1)=(\alpha ',rq_1 q_2^{\prime }/ n_1)=1$
, we have
![]() $q_2=q_2^{\prime }$
and then
$q_2=q_2^{\prime }$
and then
![]() $ \pm \bar \alpha \mp \bar \alpha ' \equiv 0 \bmod rq_1 q_2/n_1$
, which give
$ \pm \bar \alpha \mp \bar \alpha ' \equiv 0 \bmod rq_1 q_2/n_1$
, which give
![]() $\alpha \equiv \alpha ' \bmod rq_1 q_2/n_1$
. Hence
$\alpha \equiv \alpha ' \bmod rq_1 q_2/n_1$
. Hence
 $$\begin{align*}\mathfrak{C}(0) \ll \sum_{d\mid q} d \sum_{d'\mid q} d' \sideset{}{^{\star}}\sum_{\substack{\alpha \bmod rq/n_1 \\ \pm_1 m \equiv n_1\alpha \bmod d \\ \pm_1 m' \equiv n_1\alpha \bmod d'}} 1 \ll \mathop{\sum_{d\mid q} \sum_{d'\mid q}}_{(d,d')\mid (m-m')} (d,d') qr. \end{align*}$$
$$\begin{align*}\mathfrak{C}(0) \ll \sum_{d\mid q} d \sum_{d'\mid q} d' \sideset{}{^{\star}}\sum_{\substack{\alpha \bmod rq/n_1 \\ \pm_1 m \equiv n_1\alpha \bmod d \\ \pm_1 m' \equiv n_1\alpha \bmod d'}} 1 \ll \mathop{\sum_{d\mid q} \sum_{d'\mid q}}_{(d,d')\mid (m-m')} (d,d') qr. \end{align*}$$
If
![]() $n\neq 0$
, then by the Chinese Remainder Theorem, we have
$n\neq 0$
, then by the Chinese Remainder Theorem, we have
![]() $|\mathfrak {C}(n)| \leq \mathfrak {C}_1(n) \mathfrak {C}_2(n) $
, where
$|\mathfrak {C}(n)| \leq \mathfrak {C}_1(n) \mathfrak {C}_2(n) $
, where
 $$ \begin{align*} \mathfrak{C}_1(n) = \sum_{d_1\mid q_1} d_1 \sum_{d_1^{\prime}\mid q_1} d_1^{\prime} \mathop{ \sideset{}{^{\star}}\sum_{\substack{\alpha_1 \bmod rq_1/n_1 \\ \pm_1 m \equiv n_1\alpha_1 \bmod d_1}} \; \sideset{}{^{\star}}\sum_{\substack{\alpha_1^{\prime} \bmod rq_1/n_1 \\ \pm_1 m' \equiv n_1\alpha_1^{\prime} \bmod d_1^{\prime}}} }_{ \pm q_2^{\prime} \bar\alpha_1 \mp q_2 \bar\alpha_1^{\prime} \equiv -n \bmod rq_1/n_1 } 1 \end{align*} $$
$$ \begin{align*} \mathfrak{C}_1(n) = \sum_{d_1\mid q_1} d_1 \sum_{d_1^{\prime}\mid q_1} d_1^{\prime} \mathop{ \sideset{}{^{\star}}\sum_{\substack{\alpha_1 \bmod rq_1/n_1 \\ \pm_1 m \equiv n_1\alpha_1 \bmod d_1}} \; \sideset{}{^{\star}}\sum_{\substack{\alpha_1^{\prime} \bmod rq_1/n_1 \\ \pm_1 m' \equiv n_1\alpha_1^{\prime} \bmod d_1^{\prime}}} }_{ \pm q_2^{\prime} \bar\alpha_1 \mp q_2 \bar\alpha_1^{\prime} \equiv -n \bmod rq_1/n_1 } 1 \end{align*} $$
and
 $$ \begin{align*} \mathfrak{C}_2(n) = \sum_{d_2\mid q_2} d_2 \sum_{d_2^{\prime}\mid q_2^{\prime}} d_2^{\prime} \mathop{ \sideset{}{^{\star}}\sum_{\substack{\alpha_2 \bmod q_2 \\ \pm_1 m \equiv n_1\alpha_2 \bmod d_2}} \; \sideset{}{^{\star}}\sum_{\substack{\alpha_2^{\prime} \bmod q_2^{\prime} \\ \pm_1 m' \equiv n_1\alpha_2^{\prime} \bmod d_2^{\prime}}} }_{ \pm q_2^{\prime} \bar\alpha_2 \mp q_2 \bar\alpha_2^{\prime} \equiv -n \bmod q_2q_2^{\prime} } 1. \end{align*} $$
$$ \begin{align*} \mathfrak{C}_2(n) = \sum_{d_2\mid q_2} d_2 \sum_{d_2^{\prime}\mid q_2^{\prime}} d_2^{\prime} \mathop{ \sideset{}{^{\star}}\sum_{\substack{\alpha_2 \bmod q_2 \\ \pm_1 m \equiv n_1\alpha_2 \bmod d_2}} \; \sideset{}{^{\star}}\sum_{\substack{\alpha_2^{\prime} \bmod q_2^{\prime} \\ \pm_1 m' \equiv n_1\alpha_2^{\prime} \bmod d_2^{\prime}}} }_{ \pm q_2^{\prime} \bar\alpha_2 \mp q_2 \bar\alpha_2^{\prime} \equiv -n \bmod q_2q_2^{\prime} } 1. \end{align*} $$
We first consider
![]() $\mathfrak {C}_2(n)$
. From the congruence
$\mathfrak {C}_2(n)$
. From the congruence
![]() $\pm q_2^{\prime } \bar \alpha _2 \mp q_2 \bar \alpha _2^{\prime } \equiv -n \bmod q_2q_2^{\prime } $
, we have
$\pm q_2^{\prime } \bar \alpha _2 \mp q_2 \bar \alpha _2^{\prime } \equiv -n \bmod q_2q_2^{\prime } $
, we have
![]() $(q_2,q_2^{\prime })\mid n$
and
$(q_2,q_2^{\prime })\mid n$
and
![]() $\pm \frac {q_2^{\prime }}{(q_2,q_2^{\prime })}\bar {\alpha _2} \equiv -\frac {n}{(q_2,q_2^{\prime })} \bmod \frac {q_2}{(q_2,q_2^{\prime })}$
. Since
$\pm \frac {q_2^{\prime }}{(q_2,q_2^{\prime })}\bar {\alpha _2} \equiv -\frac {n}{(q_2,q_2^{\prime })} \bmod \frac {q_2}{(q_2,q_2^{\prime })}$
. Since
![]() $(n_1,q_2)=1$
, we have
$(n_1,q_2)=1$
, we have
![]() $\alpha _2 \equiv \pm _1 m \bar {n}_1 \bmod d_2$
and also
$\alpha _2 \equiv \pm _1 m \bar {n}_1 \bmod d_2$
and also
![]() $\pm q_2^{\prime } \bar \alpha _2 \equiv -n \bmod d_2$
. Therefore, we get
$\pm q_2^{\prime } \bar \alpha _2 \equiv -n \bmod d_2$
. Therefore, we get
![]() $\pm n_1 q_2^{\prime }\pm _1 mn \equiv 0 \bmod d_2$
. Similarly, we have
$\pm n_1 q_2^{\prime }\pm _1 mn \equiv 0 \bmod d_2$
. Similarly, we have
![]() $\mp n_1 q_2 \pm _1 m'n \equiv 0 \bmod d_2^{\prime }$
. Note that the congruences
$\mp n_1 q_2 \pm _1 m'n \equiv 0 \bmod d_2^{\prime }$
. Note that the congruences
![]() $ \bmod \; \frac {q_2}{(q_2,q_2^{\prime })}$
and
$ \bmod \; \frac {q_2}{(q_2,q_2^{\prime })}$
and
![]() $\bmod \; d_2$
determine
$\bmod \; d_2$
determine
![]() $\alpha _2 \bmod [q_2/(q_2,q_2^{\prime }),d_2]$
. For each given
$\alpha _2 \bmod [q_2/(q_2,q_2^{\prime }),d_2]$
. For each given
![]() $\alpha _2$
, we have at most one solution of
$\alpha _2$
, we have at most one solution of
![]() $\alpha _2^{\prime } \bmod q_2^{\prime }$
. Hence, we have
$\alpha _2^{\prime } \bmod q_2^{\prime }$
. Hence, we have
 $$\begin{align*}\mathfrak{C}_2(n) \ll \mathop{\sum\sum}_{\substack{d_2 \mid (q_2, \pm n_1 q_2^{\prime}\pm_1 mn) \\ d_2^{\prime} \mid (q_2^{\prime}, \mp n_1 q_2 \pm_1 m'n)}} d_2d_2^{\prime} \; \frac{q_2}{[q_2/(q_2,q_2^{\prime}),d_2]} \; \delta_{(q_2,q_2^{\prime})\mid n}. \end{align*}$$
$$\begin{align*}\mathfrak{C}_2(n) \ll \mathop{\sum\sum}_{\substack{d_2 \mid (q_2, \pm n_1 q_2^{\prime}\pm_1 mn) \\ d_2^{\prime} \mid (q_2^{\prime}, \mp n_1 q_2 \pm_1 m'n)}} d_2d_2^{\prime} \; \frac{q_2}{[q_2/(q_2,q_2^{\prime}),d_2]} \; \delta_{(q_2,q_2^{\prime})\mid n}. \end{align*}$$
Similarly, we have
 $$\begin{align*}\mathfrak{C}_2(n) \ll \mathop{\sum\sum}_{\substack{d_2 \mid (q_2, \pm n_1 q_2^{\prime}\pm_1 mn) \\ d_2^{\prime} \mid (q_2^{\prime}, \mp n_1 q_2 \pm_1 m'n)}} d_2d_2^{\prime} \; \frac{q_2^{\prime}}{[q_2^{\prime}/(q_2,q_2^{\prime}),d_2^{\prime}]} \; \delta_{(q_2,q_2^{\prime})\mid n}. \end{align*}$$
$$\begin{align*}\mathfrak{C}_2(n) \ll \mathop{\sum\sum}_{\substack{d_2 \mid (q_2, \pm n_1 q_2^{\prime}\pm_1 mn) \\ d_2^{\prime} \mid (q_2^{\prime}, \mp n_1 q_2 \pm_1 m'n)}} d_2d_2^{\prime} \; \frac{q_2^{\prime}}{[q_2^{\prime}/(q_2,q_2^{\prime}),d_2^{\prime}]} \; \delta_{(q_2,q_2^{\prime})\mid n}. \end{align*}$$
In
![]() $\mathfrak {C}_1(n)$
, for each value of
$\mathfrak {C}_1(n)$
, for each value of
![]() $\alpha _1$
, the congruence condition
$\alpha _1$
, the congruence condition
![]() $\operatorname {mod}\ rq_1/n_1$
determines the value of
$\operatorname {mod}\ rq_1/n_1$
determines the value of
![]() $\alpha _1^{\prime }$
, and hence, we have
$\alpha _1^{\prime }$
, and hence, we have
 $$ \begin{align*} \mathfrak{C}_1(n) \leq \sum_{d_1\mid q_1} d_1 \sum_{d_1^{\prime}\mid q_1} d_1^{\prime} \sideset{}{^{\star}}\sum_{\substack{\alpha_1 \bmod rq_1/n_1 \\ \pm_1 m \equiv n_1\alpha_1 \bmod d_1 }} 1. \end{align*} $$
$$ \begin{align*} \mathfrak{C}_1(n) \leq \sum_{d_1\mid q_1} d_1 \sum_{d_1^{\prime}\mid q_1} d_1^{\prime} \sideset{}{^{\star}}\sum_{\substack{\alpha_1 \bmod rq_1/n_1 \\ \pm_1 m \equiv n_1\alpha_1 \bmod d_1 }} 1. \end{align*} $$
Note that
![]() $\alpha _1$
is uniquely determined modulo
$\alpha _1$
is uniquely determined modulo
![]() $d_1/(d_1,n_1)$
. Since
$d_1/(d_1,n_1)$
. Since
![]() $(\frac {d_1}{(d_1,n_1)},\frac {n_1}{(d_1,n_1)})=1$
,
$(\frac {d_1}{(d_1,n_1)},\frac {n_1}{(d_1,n_1)})=1$
,
![]() $\frac {d_1}{(d_1,n_1)}\mid \frac {q_1}{(d_1,n_1)}$
and
$\frac {d_1}{(d_1,n_1)}\mid \frac {q_1}{(d_1,n_1)}$
and
![]() $\frac {n_1}{(d_1,n_1)}\mid \frac {rq_1}{(d_1,n_1)}$
, we have
$\frac {n_1}{(d_1,n_1)}\mid \frac {rq_1}{(d_1,n_1)}$
, we have
![]() $\frac {d_1}{(d_1,n_1)}\mid \frac {rq_1}{n_1}$
. Also
$\frac {d_1}{(d_1,n_1)}\mid \frac {rq_1}{n_1}$
. Also
![]() $\pm _1 m \equiv n_1\alpha _1 \bmod d_1$
has solutions only if
$\pm _1 m \equiv n_1\alpha _1 \bmod d_1$
has solutions only if
![]() $(d_1,n_1)\mid m$
. Hence, we get
$(d_1,n_1)\mid m$
. Hence, we get
 $$\begin{align*}\mathfrak{C}_1(n) \ll \frac{rq_1}{n_1} \sum_{d_1\mid q_1} \sum_{d_1^{\prime}\mid q_1} d_1^{\prime} (d_1,n_1) \delta_{(d_1,n_1)\mid m}. \end{align*}$$
$$\begin{align*}\mathfrak{C}_1(n) \ll \frac{rq_1}{n_1} \sum_{d_1\mid q_1} \sum_{d_1^{\prime}\mid q_1} d_1^{\prime} (d_1,n_1) \delta_{(d_1,n_1)\mid m}. \end{align*}$$
Similarly, by considering
![]() $\alpha _1$
-sum first, we have
$\alpha _1$
-sum first, we have
 $$\begin{align*}\mathfrak{C}_1(n) \ll \frac{rq_1}{n_1} \sum_{d_1\mid q_1} \sum_{d_1^{\prime}\mid q_1} d_1 (d_1^{\prime},n_1) \delta_{(d_1^{\prime},n_1)\mid m'}. \end{align*}$$
$$\begin{align*}\mathfrak{C}_1(n) \ll \frac{rq_1}{n_1} \sum_{d_1\mid q_1} \sum_{d_1^{\prime}\mid q_1} d_1 (d_1^{\prime},n_1) \delta_{(d_1^{\prime},n_1)\mid m'}. \end{align*}$$
This completes the proof of the lemma.
We will also need bounds for
![]() $\mathfrak {I}(n)$
. In Lemma 5.2 below, we give bounds when
$\mathfrak {I}(n)$
. In Lemma 5.2 below, we give bounds when
![]() $T^{\varepsilon } \ll \frac {NX}{PQ}\ll |T'|^{1-\varepsilon }$
. In this case, in order to get a better bound for counting, we also need to find a condition for m and
$T^{\varepsilon } \ll \frac {NX}{PQ}\ll |T'|^{1-\varepsilon }$
. In this case, in order to get a better bound for counting, we also need to find a condition for m and
![]() $m'$
, such that
$m'$
, such that
![]() $\mathfrak {I}(0)$
is not negligibly small. In Lemma 5.3 below, we consider the case
$\mathfrak {I}(0)$
is not negligibly small. In Lemma 5.3 below, we consider the case
![]() $ \frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
. In this case, we only give relatively easy bounds based on
$ \frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
. In this case, we only give relatively easy bounds based on
![]() $L^2$
-norm bounds for
$L^2$
-norm bounds for
![]() $\mathcal {I}$
, which is good enough to prove our uniform bounds.
$\mathcal {I}$
, which is good enough to prove our uniform bounds.
Lemma 5.2. Assume
![]() $T^{\varepsilon } \ll \frac {NX}{PQ}\ll |T'|^{1-\varepsilon }$
. Then we have
$T^{\varepsilon } \ll \frac {NX}{PQ}\ll |T'|^{1-\varepsilon }$
. Then we have
-
(i) for any
 $n\in \mathbb {Z}$
, we have
$n\in \mathbb {Z}$
, we have  $$\begin{align*}\mathfrak{I}(n) \ll N_2; \end{align*}$$
$$\begin{align*}\mathfrak{I}(n) \ll N_2; \end{align*}$$
-
(ii) if
 $n\gg \frac {P Q^2 n_1}{q_1 NX^2} T^{\varepsilon }$
, then we have
$n\gg \frac {P Q^2 n_1}{q_1 NX^2} T^{\varepsilon }$
, then we have
 $\mathfrak {I}(n) \ll n^{-6} T^{-A}$
;
$\mathfrak {I}(n) \ll n^{-6} T^{-A}$
; -
(iii) if
 $ \frac {N n_1}{q_1 P |T'|^2} T^{\varepsilon } + \frac {P^2 Q^3 n_1}{q_1 N^2 X^3} N^{\varepsilon } \ll |n|\ll \frac {P Q^2 n_1}{q_1 NX^2} T^{\varepsilon } $
, then
$ \frac {N n_1}{q_1 P |T'|^2} T^{\varepsilon } + \frac {P^2 Q^3 n_1}{q_1 N^2 X^3} N^{\varepsilon } \ll |n|\ll \frac {P Q^2 n_1}{q_1 NX^2} T^{\varepsilon } $
, then  $$\begin{align*}\mathfrak{I}(n) \ll N_2 \left( \frac{|n|N_2}{rq_1 q_2q_2^{\prime}/n_1} \right)^{-1/2}; \end{align*}$$
$$\begin{align*}\mathfrak{I}(n) \ll N_2 \left( \frac{|n|N_2}{rq_1 q_2q_2^{\prime}/n_1} \right)^{-1/2}; \end{align*}$$
-
(iv) if
 $q=q'$
, then we have
$q=q'$
, then we have
 $\mathfrak {I}(0) \ll T^{-A}$
, unless
$\mathfrak {I}(0) \ll T^{-A}$
, unless
 $m-m' \ll M \left (\frac {PQ}{NX} +\left (\frac {NX}{PQ}\right )^2 |T'|^{-2} \right ) T^{\varepsilon } $
.
$m-m' \ll M \left (\frac {PQ}{NX} +\left (\frac {NX}{PQ}\right )^2 |T'|^{-2} \right ) T^{\varepsilon } $
.
Proof. (i) By (4.11) and (5.4), we have
 $$ \begin{align*} &\mathfrak{I}(n) = N_2 \int_{\mathbb{R}} W\left(\xi\right) e\bigg( \pm \frac{B \xi^{1/3}}{2\pi} \sum_{0\leq \ell \leq L} Q_{\ell}^{\pm} \left(\frac{B\xi^{1/3}}{T},\frac{B\xi^{1/3}}{T'} \right) \xi_0^{\ell+1} \\ &\qquad\quad \mp \frac{B'\xi^{1/3}}{2\pi} \sum_{0\leq \ell \leq L} Q_{\ell}^{\pm} \left(\frac{B'\xi^{1/3}}{T},\frac{B'\xi^{1/3}}{T'} \right) \xi_0^{\prime \ell+1} - \frac{nN_2 \xi}{rq_1 q_2q_2^{\prime}/n_1} \bigg) \mathrm{d} \xi , \end{align*} $$
$$ \begin{align*} &\mathfrak{I}(n) = N_2 \int_{\mathbb{R}} W\left(\xi\right) e\bigg( \pm \frac{B \xi^{1/3}}{2\pi} \sum_{0\leq \ell \leq L} Q_{\ell}^{\pm} \left(\frac{B\xi^{1/3}}{T},\frac{B\xi^{1/3}}{T'} \right) \xi_0^{\ell+1} \\ &\qquad\quad \mp \frac{B'\xi^{1/3}}{2\pi} \sum_{0\leq \ell \leq L} Q_{\ell}^{\pm} \left(\frac{B'\xi^{1/3}}{T},\frac{B'\xi^{1/3}}{T'} \right) \xi_0^{\prime \ell+1} - \frac{nN_2 \xi}{rq_1 q_2q_2^{\prime}/n_1} \bigg) \mathrm{d} \xi , \end{align*} $$
where
![]() $B=\frac { N^{1/3} ( n_1^2N_2)^{1/3} }{ r^{1/3} q} $
,
$B=\frac { N^{1/3} ( n_1^2N_2)^{1/3} }{ r^{1/3} q} $
,
![]() $\xi _0 = \left (\frac {2\pi q^2 T|T'|}{mN}\right )^{1/3}$
,
$\xi _0 = \left (\frac {2\pi q^2 T|T'|}{mN}\right )^{1/3}$
,
![]() $B'=\frac { N^{1/3} ( n_1^2N_2)^{1/3} }{ r^{1/3} q'} $
,
$B'=\frac { N^{1/3} ( n_1^2N_2)^{1/3} }{ r^{1/3} q'} $
,
![]() $\xi _0^{\prime } = \left (\frac {2\pi q^{\prime 2} T|T'|}{m'N}\right )^{1/3}$
. This gives
$\xi _0^{\prime } = \left (\frac {2\pi q^{\prime 2} T|T'|}{m'N}\right )^{1/3}$
. This gives
![]() $\mathfrak {I}(n)\ll N_2$
, and hence proves (i).
$\mathfrak {I}(n)\ll N_2$
, and hence proves (i).
(ii) Let
![]() $h(\xi )$
be the phase function above. Recall that
$h(\xi )$
be the phase function above. Recall that
![]() $B\asymp B'\asymp \frac {NX}{PQ}$
and
$B\asymp B'\asymp \frac {NX}{PQ}$
and
![]() $\xi _0\asymp \xi _0^{\prime }\asymp 1$
. If
$\xi _0\asymp \xi _0^{\prime }\asymp 1$
. If
![]() $\frac {nN_2}{rq_1 q_2q_2^{\prime }/n_1} \gg \frac {NX}{PQ} T^{\varepsilon }$
, then we have
$\frac {nN_2}{rq_1 q_2q_2^{\prime }/n_1} \gg \frac {NX}{PQ} T^{\varepsilon }$
, then we have
![]() $h'(\xi ) \gg \frac {|n|N_2}{rq_1 q_2q_2^{\prime }/n_1}$
and
$h'(\xi ) \gg \frac {|n|N_2}{rq_1 q_2q_2^{\prime }/n_1}$
and
![]() $h^{(j)}(\xi ) \ll \frac {NX}{PQ}$
for
$h^{(j)}(\xi ) \ll \frac {NX}{PQ}$
for
![]() $j\geq 2$
. By Lemma 2.7 with
$j\geq 2$
. By Lemma 2.7 with
 $$\begin{align*}X=V=1, Y=\frac{NX}{PQ}, Q=1, \textrm{ and } R= \frac{|n| N_2}{rq_1 q_2q_2^{\prime}/n_1}, \end{align*}$$
$$\begin{align*}X=V=1, Y=\frac{NX}{PQ}, Q=1, \textrm{ and } R= \frac{|n| N_2}{rq_1 q_2q_2^{\prime}/n_1}, \end{align*}$$
we have
![]() $\mathfrak {I}(n) \ll n^{-6} T^{-A}$
if
$\mathfrak {I}(n) \ll n^{-6} T^{-A}$
if
![]() $\frac {nN_2}{rq_1 q_2q_2^{\prime }/n_1} \gg \frac {NX}{PQ}T^{\varepsilon }$
. Since
$\frac {nN_2}{rq_1 q_2q_2^{\prime }/n_1} \gg \frac {NX}{PQ}T^{\varepsilon }$
. Since
![]() $q=q_1q_2\sim P$
and
$q=q_1q_2\sim P$
and
![]() $N_2=\frac {r N^{2}X^3} {n_1^2 Q^3} $
, this is equivalent to
$N_2=\frac {r N^{2}X^3} {n_1^2 Q^3} $
, this is equivalent to
![]() $n\gg \frac {P Q^2 n_1}{q_1 NX^2} T^{\varepsilon }$
.
$n\gg \frac {P Q^2 n_1}{q_1 NX^2} T^{\varepsilon }$
.
(iii) Note that
 $$ \begin{align*} h'(\xi) = \pm \frac{1}{2\pi } \left( B\xi_0 - B'\xi_0^{\prime} \right) \xi^{-2/3} - \frac{\left(\frac{1}{T}+\frac{1}{T'}\right)}{6\pi } \left( B^2\xi_0^2 - B^{\prime 2}\xi_0^{\prime 2} \right) \xi^{1/3} - \frac{nN_2 }{rq_1 q_2q_2^{\prime}/n_1}+ O\left(\frac{(\frac{NX}{PQ})^3}{|T^{\prime 2}|}\right)\!. \end{align*} $$
$$ \begin{align*} h'(\xi) = \pm \frac{1}{2\pi } \left( B\xi_0 - B'\xi_0^{\prime} \right) \xi^{-2/3} - \frac{\left(\frac{1}{T}+\frac{1}{T'}\right)}{6\pi } \left( B^2\xi_0^2 - B^{\prime 2}\xi_0^{\prime 2} \right) \xi^{1/3} - \frac{nN_2 }{rq_1 q_2q_2^{\prime}/n_1}+ O\left(\frac{(\frac{NX}{PQ})^3}{|T^{\prime 2}|}\right)\!. \end{align*} $$
If
![]() $(1+(\frac {NX}{PQ})^3/|T'|^2)T^{\varepsilon } \ll \frac {nN_2}{rq_1 q_2q_2^{\prime }/n_1} \ll \frac {NX}{PQ}T^{\varepsilon }$
, that is
$(1+(\frac {NX}{PQ})^3/|T'|^2)T^{\varepsilon } \ll \frac {nN_2}{rq_1 q_2q_2^{\prime }/n_1} \ll \frac {NX}{PQ}T^{\varepsilon }$
, that is
![]() $ \frac {N n_1}{q_1 P |T'|^2} T^{\varepsilon } + \frac {P^2 Q^3 n_1}{q_1 N^2 X^3} N^{\varepsilon } \ll |n|\ll \frac {P Q^2 n_1}{q_1 NX^2} T^{\varepsilon } $
, then we have
$ \frac {N n_1}{q_1 P |T'|^2} T^{\varepsilon } + \frac {P^2 Q^3 n_1}{q_1 N^2 X^3} N^{\varepsilon } \ll |n|\ll \frac {P Q^2 n_1}{q_1 NX^2} T^{\varepsilon } $
, then we have
![]() $h'(\xi ) \gg |B\xi _0 - B'\xi _0^{\prime }| + |\frac {nN_2}{rq_1 q_2q_2^{\prime }/n_1}|$
, unless
$h'(\xi ) \gg |B\xi _0 - B'\xi _0^{\prime }| + |\frac {nN_2}{rq_1 q_2q_2^{\prime }/n_1}|$
, unless
![]() $|B\xi _0 - B'\xi _0^{\prime }| \asymp |\frac {nN_2}{rq_1 q_2q_2^{\prime }/n_1}|$
and
$|B\xi _0 - B'\xi _0^{\prime }| \asymp |\frac {nN_2}{rq_1 q_2q_2^{\prime }/n_1}|$
and
![]() $h^{(j)}(\xi ) \ll |B\xi _0 - B'\xi _0^{\prime }| + (\frac {NX}{PQ})^3/|T'|^2$
for
$h^{(j)}(\xi ) \ll |B\xi _0 - B'\xi _0^{\prime }| + (\frac {NX}{PQ})^3/|T'|^2$
for
![]() $j\geq 2$
. By Lemma 2.7 with
$j\geq 2$
. By Lemma 2.7 with
we have
![]() $\mathfrak {I}(n) \ll T^{-A}$
, unless
$\mathfrak {I}(n) \ll T^{-A}$
, unless
![]() $|B\xi _0 - B'\xi _0^{\prime }| \asymp |\frac {nN_2}{rq_1 q_2q_2^{\prime }/n_1}|$
, in which case, we have
$|B\xi _0 - B'\xi _0^{\prime }| \asymp |\frac {nN_2}{rq_1 q_2q_2^{\prime }/n_1}|$
, in which case, we have
![]() $h^{(j)}(\xi ) \asymp |\frac {nN_2}{rq_1 q_2q_2^{\prime }/n_1}| $
for
$h^{(j)}(\xi ) \asymp |\frac {nN_2}{rq_1 q_2q_2^{\prime }/n_1}| $
for
![]() $j\geq 2$
. Hence, by Lemma 2.8 with
$j\geq 2$
. Hence, by Lemma 2.8 with
 $$\begin{align*}X=1, t_1=\xi, X_1=1, \textrm{ and } Y=\frac{|n|N_2}{rq_1 q_2q_2^{\prime}/n_1}, \end{align*}$$
$$\begin{align*}X=1, t_1=\xi, X_1=1, \textrm{ and } Y=\frac{|n|N_2}{rq_1 q_2q_2^{\prime}/n_1}, \end{align*}$$
we get
![]() $\mathfrak {I}(n) \ll N_2 \left ( \frac {|n|N_2}{rq_1 q_2q_2^{\prime }/n_1} \right )^{-1/2}$
.
$\mathfrak {I}(n) \ll N_2 \left ( \frac {|n|N_2}{rq_1 q_2q_2^{\prime }/n_1} \right )^{-1/2}$
.
(iv) If
![]() $q=q'$
, then
$q=q'$
, then
![]() $B=B'$
and
$B=B'$
and
 $$ \begin{align*} &\mathfrak{I}(0) = N_2 \int_{\mathbb{R}} W\left(\xi\right) e\bigg( \pm \frac{B\xi_0}{ 2\pi } \left(1- \frac{m^{1/3}}{m^{\prime 1/3}}\right) \xi^{1/3} - \frac{B^2 \xi_0^2 }{ 4\pi } \left(\frac{1}{T}+\frac{1}{T'}\right) \left(1- \frac{m^{2/3}}{m^{\prime 2/3}}\right) \xi^{2/3} \\ &\quad\qquad\pm \frac{B \xi^{1/3}}{2\pi} \sum_{2\leq \ell \leq L} Q_{\ell}^{\pm} \left(\frac{B\xi^{1/3}}{T},\frac{B\xi^{1/3}}{T'} \right) (\xi_0^{\ell+1} - \xi_0^{\prime \ell+1}) \bigg) \mathrm{d} \xi. \end{align*} $$
$$ \begin{align*} &\mathfrak{I}(0) = N_2 \int_{\mathbb{R}} W\left(\xi\right) e\bigg( \pm \frac{B\xi_0}{ 2\pi } \left(1- \frac{m^{1/3}}{m^{\prime 1/3}}\right) \xi^{1/3} - \frac{B^2 \xi_0^2 }{ 4\pi } \left(\frac{1}{T}+\frac{1}{T'}\right) \left(1- \frac{m^{2/3}}{m^{\prime 2/3}}\right) \xi^{2/3} \\ &\quad\qquad\pm \frac{B \xi^{1/3}}{2\pi} \sum_{2\leq \ell \leq L} Q_{\ell}^{\pm} \left(\frac{B\xi^{1/3}}{T},\frac{B\xi^{1/3}}{T'} \right) (\xi_0^{\ell+1} - \xi_0^{\prime \ell+1}) \bigg) \mathrm{d} \xi. \end{align*} $$
By Lemma 2.7 as above, we have
![]() $\mathfrak {I}(0) \ll T^{-A}$
, unless
$\mathfrak {I}(0) \ll T^{-A}$
, unless
 $$\begin{align*}B \left(1- \frac{m^{1/3}}{m^{\prime 1/3}}\right) \ll \left(1+\left(\frac{NX}{PQ}\right)^3/|T'|^2 \right) T^{\varepsilon}, \end{align*}$$
$$\begin{align*}B \left(1- \frac{m^{1/3}}{m^{\prime 1/3}}\right) \ll \left(1+\left(\frac{NX}{PQ}\right)^3/|T'|^2 \right) T^{\varepsilon}, \end{align*}$$
that is,
 $$\begin{align*}m-m' \ll M \left(\frac{PQ}{NX} +\left(\frac{NX}{PQ}\right)^2 |T'|^{-2} \right) T^{\varepsilon}. \end{align*}$$
$$\begin{align*}m-m' \ll M \left(\frac{PQ}{NX} +\left(\frac{NX}{PQ}\right)^2 |T'|^{-2} \right) T^{\varepsilon}. \end{align*}$$
This completes the proof of Lemma 5.2.
Lemma 5.3. Assume
![]() $ \frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
. Then we have
$ \frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
. Then we have
-
(i) if
 $n\gg \frac {P Q^2 n_1}{q_1 NX^2} N^{\varepsilon }$
, then we have
$n\gg \frac {P Q^2 n_1}{q_1 NX^2} N^{\varepsilon }$
, then we have
 $\mathfrak {I}(n) \ll n^{-6} T^{-A}$
;
$\mathfrak {I}(n) \ll n^{-6} T^{-A}$
; -
(ii) for any
 $n\in \mathbb {Z}$
, we have
$n\in \mathbb {Z}$
, we have  $$\begin{align*}\mathfrak{I}(n) \ll N_2 T^{\varepsilon}. \end{align*}$$
$$\begin{align*}\mathfrak{I}(n) \ll N_2 T^{\varepsilon}. \end{align*}$$
Proof. (i) By (4.12) and (5.4), we have
 $$ \begin{align*} \mathfrak{I}(n) = \,&N_2 \int_{\mathbb{R}} W\left(\xi\right) \left( \frac{PQ}{NX}\right)^{1/2} \int_{\mathbb{R}} \left(\frac{ n_1^2N_2\xi}{ mq} \right)^{i\tau} W_1\left(\frac{ n_1^2 Q^3}{r N^{2}X^3}N_2\xi, \frac{\pm \tau} { \frac{NX}{PQ} } ,\frac{q}{P} \right) w^{\pm_1}(\tau) \mathrm{d} \tau \\ & \cdot \left( \frac{PQ}{NX}\right)^{1/2} \int_{\mathbb{R}} \left(\frac{ n_1^2 N_2\xi}{ m'q'} \right)^{-i\tau} \overline{W_1\left(\frac{ n_1^2 Q^3}{r N^{2}X^3}N_2\xi, \frac{\pm \tau'} { \frac{NX}{PQ} } ,\frac{q'}{P} \right) w^{\pm_1}(\tau')} \mathrm{d} \tau' e\left(\frac{-nN_2 \xi}{rq_1 q_2q_2^{\prime}/n_1} \right) \mathrm{d} \xi. \end{align*} $$
$$ \begin{align*} \mathfrak{I}(n) = \,&N_2 \int_{\mathbb{R}} W\left(\xi\right) \left( \frac{PQ}{NX}\right)^{1/2} \int_{\mathbb{R}} \left(\frac{ n_1^2N_2\xi}{ mq} \right)^{i\tau} W_1\left(\frac{ n_1^2 Q^3}{r N^{2}X^3}N_2\xi, \frac{\pm \tau} { \frac{NX}{PQ} } ,\frac{q}{P} \right) w^{\pm_1}(\tau) \mathrm{d} \tau \\ & \cdot \left( \frac{PQ}{NX}\right)^{1/2} \int_{\mathbb{R}} \left(\frac{ n_1^2 N_2\xi}{ m'q'} \right)^{-i\tau} \overline{W_1\left(\frac{ n_1^2 Q^3}{r N^{2}X^3}N_2\xi, \frac{\pm \tau'} { \frac{NX}{PQ} } ,\frac{q'}{P} \right) w^{\pm_1}(\tau')} \mathrm{d} \tau' e\left(\frac{-nN_2 \xi}{rq_1 q_2q_2^{\prime}/n_1} \right) \mathrm{d} \xi. \end{align*} $$
Changing the order of integration, we get
 $$ \begin{align*} \mathfrak{I}(n) = \,&N_2 \frac{PQ}{NX} \int_{\mathbb{R}}\left(\frac{ n_1^2N_2 }{ mq} \right)^{i\tau} w^{\pm_1}(\tau) \int_{\mathbb{R}}\left(\frac{ n_1^2 N_2}{ m'q'} \right)^{-i\tau'} \overline{ w^{\pm_1}(\tau')} \\ &\cdot \int_{\mathbb{R}} W\left(\xi\right) \xi^{i\tau-i\tau'} e\left(\frac{-nN_2 \xi}{rq_1 q_2q_2^{\prime}/n_1} \right) W_1\!\!\left(\frac{ n_1^2 Q^3}{r N^{2}X^3}N_2\xi, \frac{\pm \tau} { \frac{NX}{PQ} } ,\frac{q}{P} \right) \overline{W_1\!\!\left(\frac{ n_1^2 Q^3}{r N^{2}X^3}N_2\xi, \frac{\pm \tau'} { \frac{NX}{PQ} } ,\frac{q'}{P} \right) } \mathrm{d} \xi \mathrm{d} \tau \mathrm{d} \tau'\kern-1pt. \end{align*} $$
$$ \begin{align*} \mathfrak{I}(n) = \,&N_2 \frac{PQ}{NX} \int_{\mathbb{R}}\left(\frac{ n_1^2N_2 }{ mq} \right)^{i\tau} w^{\pm_1}(\tau) \int_{\mathbb{R}}\left(\frac{ n_1^2 N_2}{ m'q'} \right)^{-i\tau'} \overline{ w^{\pm_1}(\tau')} \\ &\cdot \int_{\mathbb{R}} W\left(\xi\right) \xi^{i\tau-i\tau'} e\left(\frac{-nN_2 \xi}{rq_1 q_2q_2^{\prime}/n_1} \right) W_1\!\!\left(\frac{ n_1^2 Q^3}{r N^{2}X^3}N_2\xi, \frac{\pm \tau} { \frac{NX}{PQ} } ,\frac{q}{P} \right) \overline{W_1\!\!\left(\frac{ n_1^2 Q^3}{r N^{2}X^3}N_2\xi, \frac{\pm \tau'} { \frac{NX}{PQ} } ,\frac{q'}{P} \right) } \mathrm{d} \xi \mathrm{d} \tau \mathrm{d} \tau'\kern-1pt. \end{align*} $$
By Lemma 2.7 in the
![]() $\xi $
-integral, we have
$\xi $
-integral, we have
![]() $\mathfrak {I}(n)\ll n^{-6} T^{-A}$
if
$\mathfrak {I}(n)\ll n^{-6} T^{-A}$
if
![]() $\frac {-nN_2 }{rq_1 q_2q_2^{\prime }/n_1} \gg \frac {NX}{PQ}T^{\varepsilon } $
, that is,
$\frac {-nN_2 }{rq_1 q_2q_2^{\prime }/n_1} \gg \frac {NX}{PQ}T^{\varepsilon } $
, that is,
 $$\begin{align*}n \gg \frac{rP^2}{n_1q_1 } \frac {n_1^2 Q^3} {r N^{2}X^3}\frac{NX}{PQ}T^{\varepsilon} = \frac{n_1 P Q^2}{q_1 N X^2} T^{\varepsilon}. \end{align*}$$
$$\begin{align*}n \gg \frac{rP^2}{n_1q_1 } \frac {n_1^2 Q^3} {r N^{2}X^3}\frac{NX}{PQ}T^{\varepsilon} = \frac{n_1 P Q^2}{q_1 N X^2} T^{\varepsilon}. \end{align*}$$
This proves (i).
(ii) By the Cauchy inequality, we have
 $$ \begin{align*} \mathfrak{I}(n) \ll N_2 \left( \int_{\mathbb{R}} W\left(\xi\right) | \mathcal{I}(N_2\xi,n_1,r,m,q_1q_2) |^2 \mathrm{d} \xi \right)^{1/2} \left( \int_{\mathbb{R}} W\left(\xi\right) | \mathcal{I}(N_2\xi,n_1,r,m',q_1q_2^{\prime}) |^2 \mathrm{d} \xi \right)^{1/2}. \end{align*} $$
$$ \begin{align*} \mathfrak{I}(n) \ll N_2 \left( \int_{\mathbb{R}} W\left(\xi\right) | \mathcal{I}(N_2\xi,n_1,r,m,q_1q_2) |^2 \mathrm{d} \xi \right)^{1/2} \left( \int_{\mathbb{R}} W\left(\xi\right) | \mathcal{I}(N_2\xi,n_1,r,m',q_1q_2^{\prime}) |^2 \mathrm{d} \xi \right)^{1/2}. \end{align*} $$
By (4.12), we have
 $$ \begin{align*} &\int_{\mathbb{R}} W\left(\xi\right) | \mathcal{I}(N_2\xi,n_1,r,m,q_1q_2) |^2 \mathrm{d} \xi = \frac{PQ}{NX} \int_{\mathbb{R}}\left(\frac{ n_1^2N_2 }{ mq} \right)^{i\tau} w^{\pm_1}(\tau) \int_{\mathbb{R}}\left(\frac{ n_1^2 N_2}{ mq} \right)^{-i\tau'} \overline{ w^{\pm_1}(\tau')} \\[7pt] &\quad\qquad\cdot \int_{\mathbb{R}} W\left(\xi\right) \xi^{i\tau-i\tau'} W_1\left(\frac{ n_1^2 Q^3}{r N^{2}X^3}N_2\xi, \frac{\pm \tau} { \frac{NX}{PQ} } ,\frac{q}{P} \right) \overline{W_1\left(\frac{ n_1^2 Q^3}{r N^{2}X^3}N_2\xi, \frac{\pm \tau'} { \frac{NX}{PQ} } ,\frac{q}{P} \right) } \mathrm{d} \xi \mathrm{d} \tau \mathrm{d} \tau'. \end{align*} $$
$$ \begin{align*} &\int_{\mathbb{R}} W\left(\xi\right) | \mathcal{I}(N_2\xi,n_1,r,m,q_1q_2) |^2 \mathrm{d} \xi = \frac{PQ}{NX} \int_{\mathbb{R}}\left(\frac{ n_1^2N_2 }{ mq} \right)^{i\tau} w^{\pm_1}(\tau) \int_{\mathbb{R}}\left(\frac{ n_1^2 N_2}{ mq} \right)^{-i\tau'} \overline{ w^{\pm_1}(\tau')} \\[7pt] &\quad\qquad\cdot \int_{\mathbb{R}} W\left(\xi\right) \xi^{i\tau-i\tau'} W_1\left(\frac{ n_1^2 Q^3}{r N^{2}X^3}N_2\xi, \frac{\pm \tau} { \frac{NX}{PQ} } ,\frac{q}{P} \right) \overline{W_1\left(\frac{ n_1^2 Q^3}{r N^{2}X^3}N_2\xi, \frac{\pm \tau'} { \frac{NX}{PQ} } ,\frac{q}{P} \right) } \mathrm{d} \xi \mathrm{d} \tau \mathrm{d} \tau'. \end{align*} $$
By Lemma 2.7 in the
![]() $\xi $
-integral, we have
$\xi $
-integral, we have
![]() $\mathfrak {I}(n)\ll T^{-A}$
if
$\mathfrak {I}(n)\ll T^{-A}$
if
![]() $|\tau -\tau '| \gg T^{\varepsilon }$
. So we have
$|\tau -\tau '| \gg T^{\varepsilon }$
. So we have
and hence,
![]() $\mathfrak {I}(n) \ll N_2 T^{\varepsilon }$
.
$\mathfrak {I}(n) \ll N_2 T^{\varepsilon }$
.
6 The zero frequency
In this section, we bound the contribution from
![]() $n=0$
in (5.3). Denote this by
$n=0$
in (5.3). Denote this by
![]() $\Omega _0$
.
$\Omega _0$
.
We first deal with the case
![]() $T^{\varepsilon } \ll \frac {NX}{PQ}\ll |T'|^{1-\varepsilon }$
. By Lemmas 5.1 and 5.2, we get
$T^{\varepsilon } \ll \frac {NX}{PQ}\ll |T'|^{1-\varepsilon }$
. By Lemmas 5.1 and 5.2, we get
 $$ \begin{align*} \Omega_0 \ll P r \frac{r N^{2}X^3} {n_1^2 Q^3} \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} \sum_{d\mid q} \sum_{d'\mid q} (d,d') \sum_{\substack{m\geq1 \\ m\asymp M}} |c_m|^2 \sum_{\substack{m'\geq1 \\ (d,d')\mid (m-m') \\ m'-m \ll M \left(\frac{PQ}{NX} +\left(\frac{NX}{PQ}\right)^2 |T'|^{-2} \right) N^{\varepsilon} }} 1. \end{align*} $$
$$ \begin{align*} \Omega_0 \ll P r \frac{r N^{2}X^3} {n_1^2 Q^3} \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} \sum_{d\mid q} \sum_{d'\mid q} (d,d') \sum_{\substack{m\geq1 \\ m\asymp M}} |c_m|^2 \sum_{\substack{m'\geq1 \\ (d,d')\mid (m-m') \\ m'-m \ll M \left(\frac{PQ}{NX} +\left(\frac{NX}{PQ}\right)^2 |T'|^{-2} \right) N^{\varepsilon} }} 1. \end{align*} $$
Here, we have used
![]() $|c_{m} c_{m'}| \leq |c_{m}|^2 + |c_{m'}|^2$
and without loss of generality only give details for the case with
$|c_{m} c_{m'}| \leq |c_{m}|^2 + |c_{m'}|^2$
and without loss of generality only give details for the case with
![]() $|c_{m}|^2$
. Note that
$|c_{m}|^2$
. Note that
 $$\begin{align*}\sum_{\substack{m'\geq1 \\ (d,d')\mid (m-m') \\ m'-m \ll M \left(\frac{PQ}{NX} +\left(\frac{NX}{PQ}\right)^2 |T'|^{-2} \right) N^{\varepsilon} }} 1 \ll N^{\varepsilon} \left( \frac{1}{(d,d')} M \left(\frac{PQ}{NX} + \left(\frac{NX}{PQ}\right)^2 |T'|^{-2} \right) + 1 \right). \end{align*}$$
$$\begin{align*}\sum_{\substack{m'\geq1 \\ (d,d')\mid (m-m') \\ m'-m \ll M \left(\frac{PQ}{NX} +\left(\frac{NX}{PQ}\right)^2 |T'|^{-2} \right) N^{\varepsilon} }} 1 \ll N^{\varepsilon} \left( \frac{1}{(d,d')} M \left(\frac{PQ}{NX} + \left(\frac{NX}{PQ}\right)^2 |T'|^{-2} \right) + 1 \right). \end{align*}$$
By (5.1), we have
 $$ \begin{align*} \Omega_0 & \ll N^{\varepsilon} \frac{r^2 P N^{2}X^3} {n_1^2 Q^3} \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} \sum_{d\mid q} \sum_{d'\mid q} (d,d') M \left( \frac{M}{(d,d')} \left(\frac{PQ}{NX} + \left(\frac{NX}{PQ}\right)^2 |T'|^{-2} \right) + 1 \right) \\[7pt] & \ll N^{\varepsilon} \frac{1}{n_1^2 q_1} \left( \frac{r^2 P^4 N^2 T^2 X^5} {Q^5} + \frac{r^2 P^7 T^2 |T'|^2 X^2} {N Q^2} + \frac{r^2 P^5 N T |T'| X^3} {Q^3} \right). \end{align*} $$
$$ \begin{align*} \Omega_0 & \ll N^{\varepsilon} \frac{r^2 P N^{2}X^3} {n_1^2 Q^3} \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} \sum_{d\mid q} \sum_{d'\mid q} (d,d') M \left( \frac{M}{(d,d')} \left(\frac{PQ}{NX} + \left(\frac{NX}{PQ}\right)^2 |T'|^{-2} \right) + 1 \right) \\[7pt] & \ll N^{\varepsilon} \frac{1}{n_1^2 q_1} \left( \frac{r^2 P^4 N^2 T^2 X^5} {Q^5} + \frac{r^2 P^7 T^2 |T'|^2 X^2} {N Q^2} + \frac{r^2 P^5 N T |T'| X^3} {Q^3} \right). \end{align*} $$
Here, we have used
![]() $M\asymp \frac {P^2 T|T'|}{N}$
. Note that
$M\asymp \frac {P^2 T|T'|}{N}$
. Note that
 $$ \begin{align} \sum_{n_1\ll Pr} n_1^2 \sum_{\frac{n_1}{(n_1,r)}\mid q_1 \mid (n_1r)^{\infty}} \frac{1}{n_1^2 q_1} \ll N^{\varepsilon} \sum_{n_1\ll Pr} \frac{(n_1,r)}{n_1} \sum_{q_1 \mid (n_1r)^{\infty}} \frac{1}{q_1} \ll N^{\varepsilon}. \end{align} $$
$$ \begin{align} \sum_{n_1\ll Pr} n_1^2 \sum_{\frac{n_1}{(n_1,r)}\mid q_1 \mid (n_1r)^{\infty}} \frac{1}{n_1^2 q_1} \ll N^{\varepsilon} \sum_{n_1\ll Pr} \frac{(n_1,r)}{n_1} \sum_{q_1 \mid (n_1r)^{\infty}} \frac{1}{q_1} \ll N^{\varepsilon}. \end{align} $$
By (5.2), the contribution from the zero frequency to
![]() $S_{r}^{\pm }(N,X,P) $
is bounded by
$S_{r}^{\pm }(N,X,P) $
is bounded by
 $$ \begin{align*} & \ll N^{\varepsilon} \frac {Q} {r P^2 T^{1/2} |T'|^{1/2} X} \left(\frac{r N^{2}X^3} {Q^3} \right)^{1/2} \\ & \hskip 60pt \cdot \left( \frac{r P^2 N T X^{5/2}} {Q^{5/2}} + \frac{r P^{7/2} T |T'| X} { N^{1/2} Q} + \frac{r P^{5/2} N^{1/2} T^{1/2} |T'|^{1/2} X^{3/2}} {Q^{3/2}} \right) \\ & \ll N^{\varepsilon} \frac{r^{1/2} N^2 T^{1/2}} { Q^{3} |T'|^{1/2} } + N^{\varepsilon} r^{1/2} N^{1/2} T^{1/2} |T'|^{1/2} + N^{\varepsilon} \frac{r^{1/2} N^{3/2} } { Q^{3/2}}. \end{align*} $$
$$ \begin{align*} & \ll N^{\varepsilon} \frac {Q} {r P^2 T^{1/2} |T'|^{1/2} X} \left(\frac{r N^{2}X^3} {Q^3} \right)^{1/2} \\ & \hskip 60pt \cdot \left( \frac{r P^2 N T X^{5/2}} {Q^{5/2}} + \frac{r P^{7/2} T |T'| X} { N^{1/2} Q} + \frac{r P^{5/2} N^{1/2} T^{1/2} |T'|^{1/2} X^{3/2}} {Q^{3/2}} \right) \\ & \ll N^{\varepsilon} \frac{r^{1/2} N^2 T^{1/2}} { Q^{3} |T'|^{1/2} } + N^{\varepsilon} r^{1/2} N^{1/2} T^{1/2} |T'|^{1/2} + N^{\varepsilon} \frac{r^{1/2} N^{3/2} } { Q^{3/2}}. \end{align*} $$
Here, we have used
![]() $X\ll T^{\varepsilon }$
and
$X\ll T^{\varepsilon }$
and
![]() $P\leq Q$
. By
$P\leq Q$
. By
![]() $Q=\frac { N^{1/2}}{K^{1/2}}$
and
$Q=\frac { N^{1/2}}{K^{1/2}}$
and
![]() $N\ll \frac {T^{3/2+\varepsilon } |T'|^{3/2}}{r^2}$
, the above is bounded by
$N\ll \frac {T^{3/2+\varepsilon } |T'|^{3/2}}{r^2}$
, the above is bounded by
 $$ \begin{align} \ll N^{1/2+\varepsilon} \frac{r^{1/2} K^{3/2} T^{1/2}} { |T'|^{1/2} } + N^{1/2+\varepsilon} r^{1/2} T^{1/2} |T'|^{1/2} + N^{1/2+\varepsilon} T^{3/8} |T'|^{3/8} K^{3/4}. \end{align} $$
$$ \begin{align} \ll N^{1/2+\varepsilon} \frac{r^{1/2} K^{3/2} T^{1/2}} { |T'|^{1/2} } + N^{1/2+\varepsilon} r^{1/2} T^{1/2} |T'|^{1/2} + N^{1/2+\varepsilon} T^{3/8} |T'|^{3/8} K^{3/4}. \end{align} $$
Now, we treat the case
![]() $\frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
. By Lemmas 5.1 and 5.3, we get
$\frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
. By Lemmas 5.1 and 5.3, we get
 $$ \begin{align*} \Omega_0 \ll P r \frac{r N^{2}X^3} {n_1^2 Q^3} \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} \sum_{d\mid q} \sum_{d'\mid q} (d,d') \\ \sum_{\substack{m\asymp M}} |c_m|^2 \sum_{\substack{m' \asymp M \\ (d,d')\mid (m-m') }} 1. \end{align*} $$
$$ \begin{align*} \Omega_0 \ll P r \frac{r N^{2}X^3} {n_1^2 Q^3} \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} \sum_{d\mid q} \sum_{d'\mid q} (d,d') \\ \sum_{\substack{m\asymp M}} |c_m|^2 \sum_{\substack{m' \asymp M \\ (d,d')\mid (m-m') }} 1. \end{align*} $$
Note that
 $$\begin{align*}\sum_{\substack{m' \asymp M \\ (d,d')\mid (m-m') }} 1 \ll \frac{1}{(d,d')} M + 1. \end{align*}$$
$$\begin{align*}\sum_{\substack{m' \asymp M \\ (d,d')\mid (m-m') }} 1 \ll \frac{1}{(d,d')} M + 1. \end{align*}$$
By (5.1), we have
 $$ \begin{align*} \Omega_0 & \ll N^{\varepsilon} \frac{r^2 P N^{2}X^3} {n_1^2 Q^3} \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} \sum_{d\mid q} \sum_{d'\mid q} (d,d') M \left( \frac{1}{(d,d')} M + 1 \right) \\ & \ll \frac{ N^{\varepsilon} } {n_1^2 q_1 } \left( \frac{r^2 P^2 N^{2}X^3 M^2 } { Q^3} + \frac{r^2 P^3 N^{2}X^3 M} {Q^3} \right). \end{align*} $$
$$ \begin{align*} \Omega_0 & \ll N^{\varepsilon} \frac{r^2 P N^{2}X^3} {n_1^2 Q^3} \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} \sum_{d\mid q} \sum_{d'\mid q} (d,d') M \left( \frac{1}{(d,d')} M + 1 \right) \\ & \ll \frac{ N^{\varepsilon} } {n_1^2 q_1 } \left( \frac{r^2 P^2 N^{2}X^3 M^2 } { Q^3} + \frac{r^2 P^3 N^{2}X^3 M} {Q^3} \right). \end{align*} $$
By (6.1) and (5.2), the contribution from the zero frequency to
![]() $S_{r}^{\pm }(N,X,P,M) $
is bounded by
$S_{r}^{\pm }(N,X,P,M) $
is bounded by
 $$ \begin{align*} & \ll N^{\varepsilon} \frac{ Q }{r N^{1/2} P X M^{1/2}} \left(\frac{r^{1/2} N X^{3/2}} {Q^{3/2}} \right) \left( \frac{r P N X^{3/2} M } { Q^{3/2}} + \frac{r P^{3/2} N X^{3/2} M^{1/2}} {Q^{3/2}} \right) \\ & \ll N^{\varepsilon} \frac{ r^{1/2} N PT}{ Q^{2} } + N^{\varepsilon} \frac{r^{1/2} N^2} { Q^{3} } + N^{\varepsilon} \frac{ r^{1/2} N^{3/2} P^{1/2} }{ Q^{2} }. \end{align*} $$
$$ \begin{align*} & \ll N^{\varepsilon} \frac{ Q }{r N^{1/2} P X M^{1/2}} \left(\frac{r^{1/2} N X^{3/2}} {Q^{3/2}} \right) \left( \frac{r P N X^{3/2} M } { Q^{3/2}} + \frac{r P^{3/2} N X^{3/2} M^{1/2}} {Q^{3/2}} \right) \\ & \ll N^{\varepsilon} \frac{ r^{1/2} N PT}{ Q^{2} } + N^{\varepsilon} \frac{r^{1/2} N^2} { Q^{3} } + N^{\varepsilon} \frac{ r^{1/2} N^{3/2} P^{1/2} }{ Q^{2} }. \end{align*} $$
Here, we have used
![]() $X\ll T^{\varepsilon }$
. Note that by the assumption
$X\ll T^{\varepsilon }$
. Note that by the assumption
![]() $\frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
, we have
$\frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
, we have
![]() $P\ll \frac {N}{Q |T'|^{1-\varepsilon }}$
. Together with
$P\ll \frac {N}{Q |T'|^{1-\varepsilon }}$
. Together with
![]() $Q=\frac { N^{1/2}}{K^{1/2}}$
and
$Q=\frac { N^{1/2}}{K^{1/2}}$
and
![]() $N\ll \frac {T^{3/2+\varepsilon } |T'|^{3/2}}{r^2}$
, the above is bounded by
$N\ll \frac {T^{3/2+\varepsilon } |T'|^{3/2}}{r^2}$
, the above is bounded by
 $$ \begin{align} \ll N^{\varepsilon} \frac{ r^{1/2} N^2 T}{ Q^{3} |T'| } + N^{\varepsilon} \frac{r^{1/2} N^{3/2} } { Q^{3/2}} \ll N^{1/2+\varepsilon} \frac{ r^{1/2} K^{3/2} T}{ |T'| } + N^{1/2+\varepsilon} T^{3/8} |T'|^{3/8} K^{3/4}. \end{align} $$
$$ \begin{align} \ll N^{\varepsilon} \frac{ r^{1/2} N^2 T}{ Q^{3} |T'| } + N^{\varepsilon} \frac{r^{1/2} N^{3/2} } { Q^{3/2}} \ll N^{1/2+\varepsilon} \frac{ r^{1/2} K^{3/2} T}{ |T'| } + N^{1/2+\varepsilon} T^{3/8} |T'|^{3/8} K^{3/4}. \end{align} $$
7 The nonzero frequencies, I
Denote the contribution from the nonzero frequencies in (5.3) by
![]() $\Omega _{\neq }$
. Our method to bound
$\Omega _{\neq }$
. Our method to bound
![]() $\Omega _{\neq }$
is similar to [Reference Huang and Xu19]. In this section, we deal with the case
$\Omega _{\neq }$
is similar to [Reference Huang and Xu19]. In this section, we deal with the case
![]() $T^{\varepsilon } \ll \frac {NX}{PQ}\ll |T'|^{1-\varepsilon }$
. By Lemmas 5.1 and 5.2, we get
$T^{\varepsilon } \ll \frac {NX}{PQ}\ll |T'|^{1-\varepsilon }$
. By Lemmas 5.1 and 5.2, we get
 $$ \begin{align} \Omega_{\neq} \ll N^{\varepsilon} \sup_{1\ll N_*\ll \frac{P Q^2 n_1}{q_1 NX^2} N^{\varepsilon}} \Omega(N_*), \end{align} $$
$$ \begin{align} \Omega_{\neq} \ll N^{\varepsilon} \sup_{1\ll N_*\ll \frac{P Q^2 n_1}{q_1 NX^2} N^{\varepsilon}} \Omega(N_*), \end{align} $$
where
 $$ \begin{align*} &\Omega(N_*) = H(N_*)\cdot N_2 \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} \sum_{\substack{m\geq1 \\ m\asymp \frac{P^2 T |T'|}{N}}} \sum_{\substack{q_2^{\prime}\sim P/q_1 \\ (q_2^{\prime},n_1r)=1}} \sum_{\substack{m'\geq1 \\ m'\asymp \frac{P^2 T |T'|}{N}}}|c_{m'}|^2 \; \frac{rq_1}{n_1} \sum_{\substack{d_1\mid q_1 \\ (d_1,n_1)\mid m}} \sum_{d_1^{\prime}\mid q_1} d_1^{\prime} (d_1,n_1) \\ &\qquad\qquad\cdot \mathop{\sum\sum}_{\substack{d_2 \mid (q_2, \pm n_1 q_2^{\prime}\pm_1 mn) \\ d_2^{\prime} \mid (q_2^{\prime}, \mp n_1 q_2 \pm_1 m'n)}} d_2d_2^{\prime} \min\left\{\frac{q_2}{[q_2/(q_2,q_2^{\prime}),d_2]},\frac{q_2^{\prime}}{[q_2^{\prime}/(q_2,q_2^{\prime}),d_2^{\prime}]} \right\} \sum_{\substack{n\asymp N_* \\ (q_2,q_2^{\prime})\mid n}} 1 , \end{align*} $$
$$ \begin{align*} &\Omega(N_*) = H(N_*)\cdot N_2 \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} \sum_{\substack{m\geq1 \\ m\asymp \frac{P^2 T |T'|}{N}}} \sum_{\substack{q_2^{\prime}\sim P/q_1 \\ (q_2^{\prime},n_1r)=1}} \sum_{\substack{m'\geq1 \\ m'\asymp \frac{P^2 T |T'|}{N}}}|c_{m'}|^2 \; \frac{rq_1}{n_1} \sum_{\substack{d_1\mid q_1 \\ (d_1,n_1)\mid m}} \sum_{d_1^{\prime}\mid q_1} d_1^{\prime} (d_1,n_1) \\ &\qquad\qquad\cdot \mathop{\sum\sum}_{\substack{d_2 \mid (q_2, \pm n_1 q_2^{\prime}\pm_1 mn) \\ d_2^{\prime} \mid (q_2^{\prime}, \mp n_1 q_2 \pm_1 m'n)}} d_2d_2^{\prime} \min\left\{\frac{q_2}{[q_2/(q_2,q_2^{\prime}),d_2]},\frac{q_2^{\prime}}{[q_2^{\prime}/(q_2,q_2^{\prime}),d_2^{\prime}]} \right\} \sum_{\substack{n\asymp N_* \\ (q_2,q_2^{\prime})\mid n}} 1 , \end{align*} $$
with
 $$ \begin{align} H(N_*) := \left\{\begin{array}{ll} \left( \frac{N_* N_2 n_1 q_1}{r P^2 }\right)^{-1/2} , & \textrm{if } \frac{N n_1}{q_1 P |T'|^2} N^{\varepsilon} + \frac{P^2 Q^3 n_1}{q_1 N^2 X^3} N^{\varepsilon} \ll N_* \ll \frac{P Q^2 n_1}{q_1 NX^2} N^{\varepsilon}, \\ 1, & \textrm{if } 1\ll N_* \ll\frac{N n_1}{q_1 P |T'|^2} N^{\varepsilon} + \frac{P^2 Q^3 n_1}{q_1 N^2 X^3} N^{\varepsilon}. \end{array} \right. \end{align} $$
$$ \begin{align} H(N_*) := \left\{\begin{array}{ll} \left( \frac{N_* N_2 n_1 q_1}{r P^2 }\right)^{-1/2} , & \textrm{if } \frac{N n_1}{q_1 P |T'|^2} N^{\varepsilon} + \frac{P^2 Q^3 n_1}{q_1 N^2 X^3} N^{\varepsilon} \ll N_* \ll \frac{P Q^2 n_1}{q_1 NX^2} N^{\varepsilon}, \\ 1, & \textrm{if } 1\ll N_* \ll\frac{N n_1}{q_1 P |T'|^2} N^{\varepsilon} + \frac{P^2 Q^3 n_1}{q_1 N^2 X^3} N^{\varepsilon}. \end{array} \right. \end{align} $$
Here, we have used
![]() $|c_{m} c_{m'}| \leq |c_{m}|^2 + |c_{m'}|^2$
and without loss of generality only give details for the case with
$|c_{m} c_{m'}| \leq |c_{m}|^2 + |c_{m'}|^2$
and without loss of generality only give details for the case with
![]() $|c_{m'}|^2$
.
$|c_{m'}|^2$
.
Changing the order of summations, we have
 $$ \begin{align*} \Omega(N_*) &= H(N_*)\cdot N_2 \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} \sum_{\substack{q_2^{\prime}\sim P/q_1 \\ (q_2^{\prime},n_1r)=1}} \frac{rq_1}{n_1} \sum_{d_1\mid q_1} \sum_{d_1^{\prime}\mid q_1} d_1^{\prime} (d_1,n_1) \sum_{d_2 \mid q_2} \sum_{d_2^{\prime} \mid q_2^{\prime}} d_2d_2^{\prime} \\ &\cdot \min\left\{\frac{q_2}{[q_2/(q_2,q_2^{\prime}),d_2]},\frac{q_2^{\prime}}{[q_2^{\prime}/(q_2,q_2^{\prime}),d_2^{\prime}]} \right\} \sum_{\substack{n\asymp N_* \\ (q_2,q_2^{\prime})\mid n}} \sum_{\substack{m'\asymp \frac{P^2 T |T'|}{N} \\ \mp n_1 q_2 \pm_1 m'n \equiv 0 \bmod d_2^{\prime}}} |c_{m'}|^2 \sum_{\substack{ m\asymp \frac{P^2 T |T'|}{N} \\ \pm n_1 q_2^{\prime}\pm_1 mn \equiv 0 \bmod d_2 \\ (d_1,n_1)\mid m}} 1. \end{align*} $$
$$ \begin{align*} \Omega(N_*) &= H(N_*)\cdot N_2 \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} \sum_{\substack{q_2^{\prime}\sim P/q_1 \\ (q_2^{\prime},n_1r)=1}} \frac{rq_1}{n_1} \sum_{d_1\mid q_1} \sum_{d_1^{\prime}\mid q_1} d_1^{\prime} (d_1,n_1) \sum_{d_2 \mid q_2} \sum_{d_2^{\prime} \mid q_2^{\prime}} d_2d_2^{\prime} \\ &\cdot \min\left\{\frac{q_2}{[q_2/(q_2,q_2^{\prime}),d_2]},\frac{q_2^{\prime}}{[q_2^{\prime}/(q_2,q_2^{\prime}),d_2^{\prime}]} \right\} \sum_{\substack{n\asymp N_* \\ (q_2,q_2^{\prime})\mid n}} \sum_{\substack{m'\asymp \frac{P^2 T |T'|}{N} \\ \mp n_1 q_2 \pm_1 m'n \equiv 0 \bmod d_2^{\prime}}} |c_{m'}|^2 \sum_{\substack{ m\asymp \frac{P^2 T |T'|}{N} \\ \pm n_1 q_2^{\prime}\pm_1 mn \equiv 0 \bmod d_2 \\ (d_1,n_1)\mid m}} 1. \end{align*} $$
Writing
![]() $q_3=(q_2,q_2^{\prime })$
, rewriting
$q_3=(q_2,q_2^{\prime })$
, rewriting
![]() $q_2$
as
$q_2$
as
![]() $q_2q_3$
and
$q_2q_3$
and
![]() $q_2^{\prime }$
and
$q_2^{\prime }$
and
![]() $q_2^{\prime }q_3$
, and changing the order of summations, we get
$q_2^{\prime }q_3$
, and changing the order of summations, we get
 $$ \begin{align*} \Omega(N_*) \ &\ll H(N_*)\cdot N_2 \frac{rq_1}{n_1} \sum_{d_1\mid q_1} \sum_{d_1^{\prime}\mid q_1} d_1^{\prime} (d_1,n_1) \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{\substack{q_2\sim P/q_1q_3 \\ (q_2,n_1r)=1}} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3 \\ (q_2^{\prime},n_1r)=1 \\ (q_2^{\prime},q_2)=1}} \\[4pt] &\quad \cdot \sum_{d_2 \mid q_2q_3} \sum_{d_2^{\prime} \mid q_2^{\prime}q_3} d_2d_2^{\prime} \min\left\{\frac{q_2}{[q_2,d_2]},\frac{q_2^{\prime}}{[q_2^{\prime},d_2^{\prime}]} \right\} \sum_{\substack{n\asymp N_* \\ q_3\mid n}} \\[4pt] &\quad\cdot \sum_{\substack{m'\asymp \frac{P^2 T |T'|}{N} \\ \mp n_1 q_2q_3 \pm_1 m'n \equiv 0 \bmod d_2^{\prime}}} |c_{m'}|^2 \sum_{\substack{ m\asymp \frac{P^2 T |T'|}{N (d_1,n_1)} \\ \pm n_1 q_2^{\prime}q_3\pm_1 (d_1,n_1)mn \equiv 0 \bmod d_2 }} 1. \end{align*} $$
$$ \begin{align*} \Omega(N_*) \ &\ll H(N_*)\cdot N_2 \frac{rq_1}{n_1} \sum_{d_1\mid q_1} \sum_{d_1^{\prime}\mid q_1} d_1^{\prime} (d_1,n_1) \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{\substack{q_2\sim P/q_1q_3 \\ (q_2,n_1r)=1}} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3 \\ (q_2^{\prime},n_1r)=1 \\ (q_2^{\prime},q_2)=1}} \\[4pt] &\quad \cdot \sum_{d_2 \mid q_2q_3} \sum_{d_2^{\prime} \mid q_2^{\prime}q_3} d_2d_2^{\prime} \min\left\{\frac{q_2}{[q_2,d_2]},\frac{q_2^{\prime}}{[q_2^{\prime},d_2^{\prime}]} \right\} \sum_{\substack{n\asymp N_* \\ q_3\mid n}} \\[4pt] &\quad\cdot \sum_{\substack{m'\asymp \frac{P^2 T |T'|}{N} \\ \mp n_1 q_2q_3 \pm_1 m'n \equiv 0 \bmod d_2^{\prime}}} |c_{m'}|^2 \sum_{\substack{ m\asymp \frac{P^2 T |T'|}{N (d_1,n_1)} \\ \pm n_1 q_2^{\prime}q_3\pm_1 (d_1,n_1)mn \equiv 0 \bmod d_2 }} 1. \end{align*} $$
Note that
![]() $((d_1,n_1),d_2)=1$
. From the congruence condition
$((d_1,n_1),d_2)=1$
. From the congruence condition
![]() $\pm n_1 q_2^{\prime }q_3\pm _1 (d_1,n_1) mn \equiv 0 \bmod d_2$
, we know m is uniquely determined modulo
$\pm n_1 q_2^{\prime }q_3\pm _1 (d_1,n_1) mn \equiv 0 \bmod d_2$
, we know m is uniquely determined modulo
![]() $d_2/(d_2,n)$
. So
$d_2/(d_2,n)$
. So
 $$ \begin{align} \sum_{\substack{ m\asymp \frac{P^2 T |T'|}{N (d_1,n_1)} \\ \pm n_1 q_2^{\prime}q_3\pm_1 (d_1,n_1)mn \equiv 0 \bmod d_2 }} 1 \ll \left(\frac{P^2 T |T'|}{N (d_1,n_1)}\frac{(d_2,n)}{d_2} + 1\right) \delta_{(d_2,n)\mid n_1q_2^{\prime}q_3}. \end{align} $$
$$ \begin{align} \sum_{\substack{ m\asymp \frac{P^2 T |T'|}{N (d_1,n_1)} \\ \pm n_1 q_2^{\prime}q_3\pm_1 (d_1,n_1)mn \equiv 0 \bmod d_2 }} 1 \ll \left(\frac{P^2 T |T'|}{N (d_1,n_1)}\frac{(d_2,n)}{d_2} + 1\right) \delta_{(d_2,n)\mid n_1q_2^{\prime}q_3}. \end{align} $$
Note that
![]() $(d_2,n_1)=1$
, and hence,
$(d_2,n_1)=1$
, and hence,
![]() $(d_2,n)\mid q_2^{\prime }q_3$
. Now rewrite
$(d_2,n)\mid q_2^{\prime }q_3$
. Now rewrite
![]() $d_2$
as
$d_2$
as
![]() $d_2d_3$
with
$d_2d_3$
with
![]() $d_2\mid q_2$
and
$d_2\mid q_2$
and
![]() $d_3\mid q_3$
and similarly for
$d_3\mid q_3$
and similarly for
![]() $d_2^{\prime }$
and
$d_2^{\prime }$
and
![]() $d_3^{\prime }$
. Since
$d_3^{\prime }$
. Since
![]() $d_3\mid q_3 \mid n$
, we have
$d_3\mid q_3 \mid n$
, we have
![]() $(d_2d_3,n) = d_3 (d_2,n/d_3)\mid q_2^{\prime }q_3$
, and therefore,
$(d_2d_3,n) = d_3 (d_2,n/d_3)\mid q_2^{\prime }q_3$
, and therefore,
![]() $(d_2,n/d_3)\mid q_2^{\prime }q_3/d_3$
. Then
$(d_2,n/d_3)\mid q_2^{\prime }q_3/d_3$
. Then
![]() $(q_2^{\prime },q_2)=1$
and
$(q_2^{\prime },q_2)=1$
and
![]() $d_2\mid q_2$
imply that
$d_2\mid q_2$
imply that
![]() $((d_2,n/d_3),q_2^{\prime })=1$
, and hence
$((d_2,n/d_3),q_2^{\prime })=1$
, and hence
We arrive at
 $$ \begin{align*} \Omega(N_*)\ &\ll H(N_*)\cdot N_2 \frac{rq_1}{n_1} \sum_{d_1\mid q_1} \sum_{d_1^{\prime}\mid q_1} d_1^{\prime} (d_1,n_1) \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3\mid q_3}d_3 \sum_{d_2 \ll P/q_1q_3} d_2 \sum_{\substack{q_2\sim P/q_1q_3 \\ d_2\mid q_2}} \\[4pt] &\quad\cdot \sum_{d_3^{\prime}\mid q_3} d_3^{\prime} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3 \\ d_2^{\prime} \mid q_2^{\prime}}} \min\left\{ \frac{(q_2/d_2,d_3)}{d_3},\frac{(q_2^{\prime}/d_2^{\prime},d_3^{\prime})}{d_3^{\prime}}\right\} \\[4pt] &\qquad \cdot \sum_{\substack{n\asymp N_* \\ q_3\mid n \\ (d_2,\frac{n}{d_3}) \mid \frac{q_3}{d_3}}} \sum_{\substack{m'\asymp \frac{P^2 T |T'|}{N} \\ \mp n_1 q_2q_3 \pm_1 m'n \equiv 0 \bmod d_2^{\prime}d_3^{\prime}}} |c_{m'}|^2 \left(\frac{P^2 T |T'|}{N (d_1,n_1)}\frac{(d_2,n/d_3)}{d_2} + 1\right). \end{align*} $$
$$ \begin{align*} \Omega(N_*)\ &\ll H(N_*)\cdot N_2 \frac{rq_1}{n_1} \sum_{d_1\mid q_1} \sum_{d_1^{\prime}\mid q_1} d_1^{\prime} (d_1,n_1) \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3\mid q_3}d_3 \sum_{d_2 \ll P/q_1q_3} d_2 \sum_{\substack{q_2\sim P/q_1q_3 \\ d_2\mid q_2}} \\[4pt] &\quad\cdot \sum_{d_3^{\prime}\mid q_3} d_3^{\prime} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3 \\ d_2^{\prime} \mid q_2^{\prime}}} \min\left\{ \frac{(q_2/d_2,d_3)}{d_3},\frac{(q_2^{\prime}/d_2^{\prime},d_3^{\prime})}{d_3^{\prime}}\right\} \\[4pt] &\qquad \cdot \sum_{\substack{n\asymp N_* \\ q_3\mid n \\ (d_2,\frac{n}{d_3}) \mid \frac{q_3}{d_3}}} \sum_{\substack{m'\asymp \frac{P^2 T |T'|}{N} \\ \mp n_1 q_2q_3 \pm_1 m'n \equiv 0 \bmod d_2^{\prime}d_3^{\prime}}} |c_{m'}|^2 \left(\frac{P^2 T |T'|}{N (d_1,n_1)}\frac{(d_2,n/d_3)}{d_2} + 1\right). \end{align*} $$
According to whether
![]() $\mp n_1 q_2 q_3 \pm _1 m'n$
is zero or not, we have
$\mp n_1 q_2 q_3 \pm _1 m'n$
is zero or not, we have
where
 $$ \begin{align*} &\Omega_{1} = H(N_*)\cdot N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3\mid q_3}d_3 \sum_{d_2 \ll P/q_1q_3} d_2\sum_{\substack{q_2\sim P/q_1q_3 \\ d_2\mid q_2}} \frac{(q_2/d_2,d_3)}{d_3} \sum_{\substack{m'\asymp \frac{P^2 T |T'|}{N} }} |c_{m'}|^2 \\ &\quad\cdot \sum_{\substack{n\asymp N_* \\ q_3\mid n \\ \mp n_1 q_2q_3 \pm_1 m'n \neq 0}} \left( \frac{P^2 T |T'|}{N q_1}\frac{(d_2,n/d_3)}{d_2} + 1\right) \sum_{d_3^{\prime}\mid q_3} d_3^{\prime} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 \\ \mp n_1 q_2q_3 \pm_1 m'n \equiv 0 \bmod d_2^{\prime}d_3^{\prime} }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3 \\ d_2^{\prime} \mid q_2^{\prime}}}1 \end{align*} $$
$$ \begin{align*} &\Omega_{1} = H(N_*)\cdot N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3\mid q_3}d_3 \sum_{d_2 \ll P/q_1q_3} d_2\sum_{\substack{q_2\sim P/q_1q_3 \\ d_2\mid q_2}} \frac{(q_2/d_2,d_3)}{d_3} \sum_{\substack{m'\asymp \frac{P^2 T |T'|}{N} }} |c_{m'}|^2 \\ &\quad\cdot \sum_{\substack{n\asymp N_* \\ q_3\mid n \\ \mp n_1 q_2q_3 \pm_1 m'n \neq 0}} \left( \frac{P^2 T |T'|}{N q_1}\frac{(d_2,n/d_3)}{d_2} + 1\right) \sum_{d_3^{\prime}\mid q_3} d_3^{\prime} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 \\ \mp n_1 q_2q_3 \pm_1 m'n \equiv 0 \bmod d_2^{\prime}d_3^{\prime} }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3 \\ d_2^{\prime} \mid q_2^{\prime}}}1 \end{align*} $$
and
 $$ \begin{align*} &\Omega_{2} = H(N_*)\cdot N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3^{\prime}\mid q_3} d_3^{\prime} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3 \\ d_2^{\prime} \mid q_2^{\prime}}} \frac{(q_2^{\prime}/d_2^{\prime},d_3^{\prime})}{d_3^{\prime}} \sum_{\substack{m'\asymp \frac{P^2 T |T'|}{N} }} |c_{m'}|^2 \\ &\quad \cdot \sum_{\substack{n\asymp N_* \\ q_3\mid n }} \sum_{d_3\mid q_3}d_3 \sum_{\substack{d_2 \ll P/q_1q_3 \\ (d_2,\frac{n}{d_3}) \mid \frac{q_3}{d_3}} } d_2 \left( \frac{P^2 T |T'|}{Nq_1}\frac{(d_2,n/d_3)}{d_2} + 1\right) \sum_{\substack{q_2\sim P/q_1q_3 \\ d_2\mid q_2 \\ \mp n_1 q_2q_3 \pm_1 m'n =0 }} 1. \end{align*} $$
$$ \begin{align*} &\Omega_{2} = H(N_*)\cdot N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3^{\prime}\mid q_3} d_3^{\prime} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3 \\ d_2^{\prime} \mid q_2^{\prime}}} \frac{(q_2^{\prime}/d_2^{\prime},d_3^{\prime})}{d_3^{\prime}} \sum_{\substack{m'\asymp \frac{P^2 T |T'|}{N} }} |c_{m'}|^2 \\ &\quad \cdot \sum_{\substack{n\asymp N_* \\ q_3\mid n }} \sum_{d_3\mid q_3}d_3 \sum_{\substack{d_2 \ll P/q_1q_3 \\ (d_2,\frac{n}{d_3}) \mid \frac{q_3}{d_3}} } d_2 \left( \frac{P^2 T |T'|}{Nq_1}\frac{(d_2,n/d_3)}{d_2} + 1\right) \sum_{\substack{q_2\sim P/q_1q_3 \\ d_2\mid q_2 \\ \mp n_1 q_2q_3 \pm_1 m'n =0 }} 1. \end{align*} $$
7.1 The nonzero cases
If
![]() $\mp n_1 q_2 q_3 \pm _1 m'n \neq 0$
, then the innermost sums over
$\mp n_1 q_2 q_3 \pm _1 m'n \neq 0$
, then the innermost sums over
![]() $d_3^{\prime }$
,
$d_3^{\prime }$
,
![]() $d_2^{\prime }$
and
$d_2^{\prime }$
and
![]() $q_2^{\prime }$
in
$q_2^{\prime }$
in
![]() $\Omega _1$
are bounded by
$\Omega _1$
are bounded by
 $$ \begin{align} \ll \sum_{d_3^{\prime}\mid q_3} d_3^{\prime} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 \\ \mp n_1 q_2q_3 \pm_1 m'n \equiv 0 \bmod d_2^{\prime}d_3^{\prime}}} \frac{P}{q_1q_3 } \ll N^{\varepsilon} \frac{P}{q_1}. \end{align} $$
$$ \begin{align} \ll \sum_{d_3^{\prime}\mid q_3} d_3^{\prime} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 \\ \mp n_1 q_2q_3 \pm_1 m'n \equiv 0 \bmod d_2^{\prime}d_3^{\prime}}} \frac{P}{q_1q_3 } \ll N^{\varepsilon} \frac{P}{q_1}. \end{align} $$
Hence, we have
 $$ \begin{align*} \Omega_{1} \ll\ &N^{\varepsilon} H(N_*)\cdot N_2 \frac{rq_1^3}{n_1} \frac{P}{q_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3\mid q_3} \sum_{d_2 \ll P/q_1q_3} d_2\sum_{\substack{q_2\sim P/q_1q_3 \\ (q_2,n_1r)=1 \\ d_2\mid q_2}} (q_2/d_2,d_3) \\ &\quad\cdot \sum_{\substack{m'\asymp \frac{P^2 T |T'|}{N} }} |c_{m'}|^2 \sum_{\substack{n\asymp N_* \\ q_3\mid n}} \left( \frac{P^2 T |T'|}{Nq_1}\frac{(d_2d_3,n)}{d_2d_3} + 1\right). \end{align*} $$
$$ \begin{align*} \Omega_{1} \ll\ &N^{\varepsilon} H(N_*)\cdot N_2 \frac{rq_1^3}{n_1} \frac{P}{q_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3\mid q_3} \sum_{d_2 \ll P/q_1q_3} d_2\sum_{\substack{q_2\sim P/q_1q_3 \\ (q_2,n_1r)=1 \\ d_2\mid q_2}} (q_2/d_2,d_3) \\ &\quad\cdot \sum_{\substack{m'\asymp \frac{P^2 T |T'|}{N} }} |c_{m'}|^2 \sum_{\substack{n\asymp N_* \\ q_3\mid n}} \left( \frac{P^2 T |T'|}{Nq_1}\frac{(d_2d_3,n)}{d_2d_3} + 1\right). \end{align*} $$
Note that we have
 $$ \begin{align} q_3 \sum_{\substack{ n\sim N_* \\ q_3 \mid n}} (d,n) &\ll q_3 \sum_{n\sim N_*/q_3} (d,q_3 n) \leq q_3 \sum_{n\sim N_*/q_3} (d,n) (d,q_3)\notag \\ &\quad\leq (d,q_3) q_3 \sum_{d'\mid d} d' \sum_{n\sim N_*/q_3,\; d'\mid n} 1 \ll d^{\varepsilon} (d,q_3) N_*. \end{align} $$
$$ \begin{align} q_3 \sum_{\substack{ n\sim N_* \\ q_3 \mid n}} (d,n) &\ll q_3 \sum_{n\sim N_*/q_3} (d,q_3 n) \leq q_3 \sum_{n\sim N_*/q_3} (d,n) (d,q_3)\notag \\ &\quad\leq (d,q_3) q_3 \sum_{d'\mid d} d' \sum_{n\sim N_*/q_3,\; d'\mid n} 1 \ll d^{\varepsilon} (d,q_3) N_*. \end{align} $$
By (5.1), we have
 $$ \begin{align*} \Omega_{1} & \ll N^{\varepsilon} H(N_*)\cdot N_2 N_* \frac{rq_1^3}{n_1} \frac{P}{q_1} \frac{P^2 T |T'|}{N} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} \sum_{d_3\mid q_3} \\ & \hskip 60pt \cdot \sum_{d_2 \ll P/q_1q_3} d_2 \sum_{\substack{q_2\sim P/q_1q_3 \\ (q_2,n_1r)=1 \\ d_2\mid q_2}} (q_2/d_2,d_3) \left(\frac{P^2 T |T'|}{Nq_1}\frac{ (d_2,q_3) }{d_2} + 1\right) \\ & \ll N^{\varepsilon} H(N_*)\cdot N_2 N_* \frac{rq_1^3}{n_1} \frac{P}{q_1} \frac{P^2 T |T'|}{N} \left(\frac{P^2 T |T'|}{Nq_1}\frac{P}{q_1} + \frac{P^2}{q_1^2} \right). \end{align*} $$
$$ \begin{align*} \Omega_{1} & \ll N^{\varepsilon} H(N_*)\cdot N_2 N_* \frac{rq_1^3}{n_1} \frac{P}{q_1} \frac{P^2 T |T'|}{N} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} \sum_{d_3\mid q_3} \\ & \hskip 60pt \cdot \sum_{d_2 \ll P/q_1q_3} d_2 \sum_{\substack{q_2\sim P/q_1q_3 \\ (q_2,n_1r)=1 \\ d_2\mid q_2}} (q_2/d_2,d_3) \left(\frac{P^2 T |T'|}{Nq_1}\frac{ (d_2,q_3) }{d_2} + 1\right) \\ & \ll N^{\varepsilon} H(N_*)\cdot N_2 N_* \frac{rq_1^3}{n_1} \frac{P}{q_1} \frac{P^2 T |T'|}{N} \left(\frac{P^2 T |T'|}{Nq_1}\frac{P}{q_1} + \frac{P^2}{q_1^2} \right). \end{align*} $$
Recall that
![]() $N_2 = \frac {r N^{2}X^3} {n_1^2 Q^3} $
. If
$N_2 = \frac {r N^{2}X^3} {n_1^2 Q^3} $
. If
![]() $\frac {N n_1}{q_1 P |T'|^2} N^{\varepsilon } + \frac {P^2 Q^3 n_1}{q_1 N^2 X^3} N^{\varepsilon } \ll N_* \ll \frac {P Q^2 n_1}{q_1 NX^2} N^{\varepsilon }$
, then by (7.2), we obtain
$\frac {N n_1}{q_1 P |T'|^2} N^{\varepsilon } + \frac {P^2 Q^3 n_1}{q_1 N^2 X^3} N^{\varepsilon } \ll N_* \ll \frac {P Q^2 n_1}{q_1 NX^2} N^{\varepsilon }$
, then by (7.2), we obtain
 $$ \begin{align*} \Omega_{1} & \ll N^{\varepsilon} \left( \frac{r N^{2}X^3} {n_1^2 Q^3}\right)^{1/2} \frac{rq_1^3}{n_1} \frac{r^{1/2} P}{ q_1^{1/2} n_1^{1/2}} \frac{P}{q_1} \left(\frac{P Q^2 n_1}{q_1 NX^2}\right)^{1/2} \frac{P^2 T |T'|}{N} \left(\frac{P^2 T |T'|}{Nq_1}\frac{P}{q_1} + \frac{P^2}{q_1^2} \right) \\ & \ll \frac{r^2 P^{15/2} T^2 |T'|^2 X^{1/2}} { n_1^{2} q_1 Q^{1/2} N^{3/2} } + \frac{r^2 P^{13/2} T |T'| X^{1/2}} { n_1^{2} q_1 Q^{1/2} N^{1/2} }. \end{align*} $$
$$ \begin{align*} \Omega_{1} & \ll N^{\varepsilon} \left( \frac{r N^{2}X^3} {n_1^2 Q^3}\right)^{1/2} \frac{rq_1^3}{n_1} \frac{r^{1/2} P}{ q_1^{1/2} n_1^{1/2}} \frac{P}{q_1} \left(\frac{P Q^2 n_1}{q_1 NX^2}\right)^{1/2} \frac{P^2 T |T'|}{N} \left(\frac{P^2 T |T'|}{Nq_1}\frac{P}{q_1} + \frac{P^2}{q_1^2} \right) \\ & \ll \frac{r^2 P^{15/2} T^2 |T'|^2 X^{1/2}} { n_1^{2} q_1 Q^{1/2} N^{3/2} } + \frac{r^2 P^{13/2} T |T'| X^{1/2}} { n_1^{2} q_1 Q^{1/2} N^{1/2} }. \end{align*} $$
By (5.2) and (6.1), the contribution from
![]() $\Omega _{1}$
to
$\Omega _{1}$
to
![]() $S_{r}^{\pm }(N,X,P) $
is bounded by
$S_{r}^{\pm }(N,X,P) $
is bounded by
 $$ \begin{align*} & \ll N^{\varepsilon} \frac {Q} {r P^2 T^{1/2} |T'|^{1/2} X} \left(\frac{r N^{2}X^3} {Q^3} \right)^{1/2} \left( \frac{r P^{15/4} T |T'| X^{1/4}} { Q^{1/4} N^{3/4} } + \frac{r P^{13/4} T^{1/2} |T'|^{1/2} X^{1/4}} { Q^{1/4} N^{1/4} } \right) \\ & \ll N^{\varepsilon} r^{1/2} N^{1/4} Q T^{1/2} |T'|^{1/2} + N^{\varepsilon} r^{1/2} N^{3/4} Q^{1/2}. \end{align*} $$
$$ \begin{align*} & \ll N^{\varepsilon} \frac {Q} {r P^2 T^{1/2} |T'|^{1/2} X} \left(\frac{r N^{2}X^3} {Q^3} \right)^{1/2} \left( \frac{r P^{15/4} T |T'| X^{1/4}} { Q^{1/4} N^{3/4} } + \frac{r P^{13/4} T^{1/2} |T'|^{1/2} X^{1/4}} { Q^{1/4} N^{1/4} } \right) \\ & \ll N^{\varepsilon} r^{1/2} N^{1/4} Q T^{1/2} |T'|^{1/2} + N^{\varepsilon} r^{1/2} N^{3/4} Q^{1/2}. \end{align*} $$
By
![]() $Q=\frac { N^{1/2}}{K^{1/2}}$
and
$Q=\frac { N^{1/2}}{K^{1/2}}$
and
![]() $N\ll \frac {T^{3/2+\varepsilon } |T'|^{3/2}}{r^2}$
, the above is bounded by
$N\ll \frac {T^{3/2+\varepsilon } |T'|^{3/2}}{r^2}$
, the above is bounded by
If
![]() $1\ll N_* \ll \frac {N n_1}{q_1 P |T'|^2} N^{\varepsilon } + \frac {P^2 Q^3 n_1}{q_1 N^2 X^3} N^{\varepsilon } $
, then by (7.2), we obtain
$1\ll N_* \ll \frac {N n_1}{q_1 P |T'|^2} N^{\varepsilon } + \frac {P^2 Q^3 n_1}{q_1 N^2 X^3} N^{\varepsilon } $
, then by (7.2), we obtain
 $$ \begin{align*} \Omega_{1} & \ll N^{\varepsilon} \frac{r N^{2}X^3} {n_1^2 Q^3} \frac{rq_1^3}{n_1} \frac{P}{q_1} \left( \frac{N n_1}{q_1 P |T'|^2} + \frac{P^2 Q^3 n_1}{q_1 N^2 X^3} \right) \frac{P^2 T|T'|}{N} \left(\frac{P^2 T|T'|}{Nq_1}\frac{P}{q_1} + \frac{P^2}{q_1^2} \right) \\ & \ll N^{\varepsilon} \frac{r^2 N P^5 T|T'| X^3} {n_1^2 q_1 Q^3} \left( \frac{T}{|T'|} + \frac{P^3 Q^3 T|T'|}{N^3 X^3} + \frac{N}{P |T'|^2} + \frac{P^2 Q^3}{N^2 X^3} \right). \end{align*} $$
$$ \begin{align*} \Omega_{1} & \ll N^{\varepsilon} \frac{r N^{2}X^3} {n_1^2 Q^3} \frac{rq_1^3}{n_1} \frac{P}{q_1} \left( \frac{N n_1}{q_1 P |T'|^2} + \frac{P^2 Q^3 n_1}{q_1 N^2 X^3} \right) \frac{P^2 T|T'|}{N} \left(\frac{P^2 T|T'|}{Nq_1}\frac{P}{q_1} + \frac{P^2}{q_1^2} \right) \\ & \ll N^{\varepsilon} \frac{r^2 N P^5 T|T'| X^3} {n_1^2 q_1 Q^3} \left( \frac{T}{|T'|} + \frac{P^3 Q^3 T|T'|}{N^3 X^3} + \frac{N}{P |T'|^2} + \frac{P^2 Q^3}{N^2 X^3} \right). \end{align*} $$
By (5.2) and (6.1), the contribution from
![]() $\Omega _{1}$
to
$\Omega _{1}$
to
![]() $S_{r}^{\pm }(N,X,P) $
is bounded by
$S_{r}^{\pm }(N,X,P) $
is bounded by
 $$ \begin{align*} & \ll N^{\varepsilon} \frac {Q} {r P^2 T^{1/2}|T'|^{1/2} X} \left( \frac{r N^{2}X^3} {Q^3} \right)^{1/2} \frac{r N^{1/2} P^{5/2} T^{1/2}|T'|^{1/2} X^{3/2}} {Q^{3/2}} \\ & \hskip 60pt \cdot \left( \frac{T^{1/2}}{|T'|^{1/2}} + \frac{P^{3/2} Q^{3/2} T^{1/2}|T'|^{1/2}}{N^{3/2} X^{3/2}} + \frac{N^{1/2}}{P^{1/2} |T'|} + \frac{P Q^{3/2}}{N X^{3/2}} \right) \\ & \ll N^{\varepsilon} \frac{r^{1/2} N^{3/2} } {Q^{3/2}}\frac{T^{1/2}}{|T'|^{1/2}} + N^{\varepsilon} r^{1/2} Q^{3/2} T^{1/2}|T'|^{1/2} + N^{\varepsilon} \frac{r^{1/2} N^{2}} {Q^{2} |T'|} + N^{\varepsilon} r^{1/2} N^{1/2} Q. \end{align*} $$
$$ \begin{align*} & \ll N^{\varepsilon} \frac {Q} {r P^2 T^{1/2}|T'|^{1/2} X} \left( \frac{r N^{2}X^3} {Q^3} \right)^{1/2} \frac{r N^{1/2} P^{5/2} T^{1/2}|T'|^{1/2} X^{3/2}} {Q^{3/2}} \\ & \hskip 60pt \cdot \left( \frac{T^{1/2}}{|T'|^{1/2}} + \frac{P^{3/2} Q^{3/2} T^{1/2}|T'|^{1/2}}{N^{3/2} X^{3/2}} + \frac{N^{1/2}}{P^{1/2} |T'|} + \frac{P Q^{3/2}}{N X^{3/2}} \right) \\ & \ll N^{\varepsilon} \frac{r^{1/2} N^{3/2} } {Q^{3/2}}\frac{T^{1/2}}{|T'|^{1/2}} + N^{\varepsilon} r^{1/2} Q^{3/2} T^{1/2}|T'|^{1/2} + N^{\varepsilon} \frac{r^{1/2} N^{2}} {Q^{2} |T'|} + N^{\varepsilon} r^{1/2} N^{1/2} Q. \end{align*} $$
Here, we have used
![]() $X\ll T^{\varepsilon }$
. By
$X\ll T^{\varepsilon }$
. By
![]() $Q=\frac { N^{1/2}}{K^{1/2}}$
and
$Q=\frac { N^{1/2}}{K^{1/2}}$
and
![]() $N\ll \frac {T^{3/2+\varepsilon } |T'|^{3/2}}{r^2}$
, the above is bounded by
$N\ll \frac {T^{3/2+\varepsilon } |T'|^{3/2}}{r^2}$
, the above is bounded by
 $$ \begin{align} \ll N^{1/2+\varepsilon} \frac{K^{3/4} T^{7/8}}{|T'|^{1/8}} + N^{1/2+\varepsilon} \frac{ T^{7/8}|T'|^{7/8}}{K^{3/4}} + N^{1/2+\varepsilon} \frac{T^{3/4} K} { |T'|^{1/4}} + N^{1/2+\varepsilon} \frac{T^{3/4}|T'|^{3/4}}{K^{1/2}}. \end{align} $$
$$ \begin{align} \ll N^{1/2+\varepsilon} \frac{K^{3/4} T^{7/8}}{|T'|^{1/8}} + N^{1/2+\varepsilon} \frac{ T^{7/8}|T'|^{7/8}}{K^{3/4}} + N^{1/2+\varepsilon} \frac{T^{3/4} K} { |T'|^{1/4}} + N^{1/2+\varepsilon} \frac{T^{3/4}|T'|^{3/4}}{K^{1/2}}. \end{align} $$
7.2 The zero case
If
![]() $\mp n_1 q_2 q_3 \pm _1 m'n = 0$
, then we have
$\mp n_1 q_2 q_3 \pm _1 m'n = 0$
, then we have
![]() $n\asymp \frac {n_1 q_2 q_3}{m'} \ll \frac {n_1 N}{q_1 PT|T'|}$
. Since
$n\asymp \frac {n_1 q_2 q_3}{m'} \ll \frac {n_1 N}{q_1 PT|T'|}$
. Since
![]() $n\asymp N_*$
, we have
$n\asymp N_*$
, we have
![]() $\Omega _2=0$
, unless
$\Omega _2=0$
, unless
![]() $N_* \ll \frac {n_1 N}{q_1 PT|T'|}$
, in which case, by (7.2), we have
$N_* \ll \frac {n_1 N}{q_1 PT|T'|}$
, in which case, by (7.2), we have
![]() $H(N_*)=1$
. In
$H(N_*)=1$
. In
![]() $\Omega _2$
, we should consider the sums over
$\Omega _2$
, we should consider the sums over
![]() $d_2,\ q_2, \ q_3$
first. Since
$d_2,\ q_2, \ q_3$
first. Since
![]() $d_2\mid q_2$
, we rewrite
$d_2\mid q_2$
, we rewrite
![]() $q_2$
as
$q_2$
as
![]() $d_2 q_2$
. Hence
$d_2 q_2$
. Hence
 $$ \begin{align*} \Omega_{2}\ &\ll N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3^{\prime}\mid q_3} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3 \\ d_2^{\prime} \mid q_2^{\prime}}} (q_2^{\prime}/d_2^{\prime},d_3^{\prime}) \sum_{\substack{m'\asymp \frac{P^2 T |T'|}{N} }} |c_{m'}|^2 \\ &\quad\cdot \sum_{\substack{1 \ll |n|\ll \frac{n_1 N}{q_1 PT |T'|} \\ q_3\mid n}} \sum_{d_3\mid q_3} d_3 \sum_{\substack{d_2 \ll P/q_1q_3 \\ (d_2,\frac{n}{d_3}) \mid \frac{q_3}{d_3} }} d_2 \left(\frac{P^2 T |T'|}{Nq_1}\frac{(d_2,n/d_3)}{d_2} + 1\right) \sum_{\substack{q_2\sim P/q_1q_3d_2 \\ \mp n_1 d_2 q_2q_3 \pm_1 m'n =0 } } 1. \end{align*} $$
$$ \begin{align*} \Omega_{2}\ &\ll N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3^{\prime}\mid q_3} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3 \\ d_2^{\prime} \mid q_2^{\prime}}} (q_2^{\prime}/d_2^{\prime},d_3^{\prime}) \sum_{\substack{m'\asymp \frac{P^2 T |T'|}{N} }} |c_{m'}|^2 \\ &\quad\cdot \sum_{\substack{1 \ll |n|\ll \frac{n_1 N}{q_1 PT |T'|} \\ q_3\mid n}} \sum_{d_3\mid q_3} d_3 \sum_{\substack{d_2 \ll P/q_1q_3 \\ (d_2,\frac{n}{d_3}) \mid \frac{q_3}{d_3} }} d_2 \left(\frac{P^2 T |T'|}{Nq_1}\frac{(d_2,n/d_3)}{d_2} + 1\right) \sum_{\substack{q_2\sim P/q_1q_3d_2 \\ \mp n_1 d_2 q_2q_3 \pm_1 m'n =0 } } 1. \end{align*} $$
Note that
![]() $d_2d_3\leq d_2q_3\ll P/q_1$
and the choices of
$d_2d_3\leq d_2q_3\ll P/q_1$
and the choices of
![]() $(d_2,d_3,q_2)$
are at most
$(d_2,d_3,q_2)$
are at most
![]() $N^{\varepsilon }$
for each fixed
$N^{\varepsilon }$
for each fixed
![]() $m',n$
as
$m',n$
as
![]() $d_2d_3q_2 \mid d_2 q_2q_3 \mid m'n$
. Note that
$d_2d_3q_2 \mid d_2 q_2q_3 \mid m'n$
. Note that
![]() $ (d_2,\frac {n}{d_3}) \mid \frac {q_3}{d_3}$
gives
$ (d_2,\frac {n}{d_3}) \mid \frac {q_3}{d_3}$
gives
![]() $(d_2,n/d_3) d_3 \leq q_3$
. Hence
$(d_2,n/d_3) d_3 \leq q_3$
. Hence
 $$ \begin{align*} \Omega_{2}\ \ll N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3^{\prime}\mid q_3} &\sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3d_2^{\prime} }} (q_2^{\prime},d_3^{\prime}) \\ &\cdot \sum_{\substack{m'\asymp \frac{P^2 T |T'|}{N} }} |c_{m'}|^2 \sum_{\substack{1 \ll |n|\ll \frac{n_1 N}{q_1 PT |T'|} \\ q_3\mid n}} \left(\frac{P^2 T |T'|}{Nq_1} q_3 + \frac{P}{q_1} \right). \end{align*} $$
$$ \begin{align*} \Omega_{2}\ \ll N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3^{\prime}\mid q_3} &\sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3d_2^{\prime} }} (q_2^{\prime},d_3^{\prime}) \\ &\cdot \sum_{\substack{m'\asymp \frac{P^2 T |T'|}{N} }} |c_{m'}|^2 \sum_{\substack{1 \ll |n|\ll \frac{n_1 N}{q_1 PT |T'|} \\ q_3\mid n}} \left(\frac{P^2 T |T'|}{Nq_1} q_3 + \frac{P}{q_1} \right). \end{align*} $$
 $$ \begin{align*} \Omega_{2} \ll N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} \sum_{d_3^{\prime}\mid q_3} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3d_2^{\prime} }} (q_2^{\prime},d_3^{\prime}) \left( \frac{n_1 N}{q_1 PT |T'|} \right) \left(\frac{P^2 T |T'|}{Nq_1} q_3 + \frac{P}{q_1} \right) \frac{P^2 T |T'|}{N}. \end{align*} $$
$$ \begin{align*} \Omega_{2} \ll N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} \sum_{d_3^{\prime}\mid q_3} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3d_2^{\prime} }} (q_2^{\prime},d_3^{\prime}) \left( \frac{n_1 N}{q_1 PT |T'|} \right) \left(\frac{P^2 T |T'|}{Nq_1} q_3 + \frac{P}{q_1} \right) \frac{P^2 T |T'|}{N}. \end{align*} $$
Changing the order of summations, we get
 $$ \begin{align*} \Omega_{2} & \ll N_2 \frac{rq_1^3}{n_1} \frac{n_1 N}{q_1 PT |T'|} \frac{P^2 T |T'|}{N} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} \!\!\!\left(\frac{P^2 T |T'|}{Nq_1} q_3 + \frac{P}{q_1} \right) \!\sum_{d_3^{\prime}\mid q_3} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3d_2^{\prime} }} \!(q_2^{\prime},d_3^{\prime}) \\ & \ll N^{\varepsilon} N_2 rq_1^2 P \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} \left(\frac{P^2 T |T'|}{Nq_1} q_3 + \frac{P}{q_1} \right) \frac{P^2}{q_1^2q_3^2} \ll N^{\varepsilon} \frac{r^2 N^{2} P^4 X^3} {n_1^2 q_1 Q^3} \left(\frac{P T |T'|}{N} + 1 \right). \end{align*} $$
$$ \begin{align*} \Omega_{2} & \ll N_2 \frac{rq_1^3}{n_1} \frac{n_1 N}{q_1 PT |T'|} \frac{P^2 T |T'|}{N} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} \!\!\!\left(\frac{P^2 T |T'|}{Nq_1} q_3 + \frac{P}{q_1} \right) \!\sum_{d_3^{\prime}\mid q_3} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3d_2^{\prime} }} \!(q_2^{\prime},d_3^{\prime}) \\ & \ll N^{\varepsilon} N_2 rq_1^2 P \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} \left(\frac{P^2 T |T'|}{Nq_1} q_3 + \frac{P}{q_1} \right) \frac{P^2}{q_1^2q_3^2} \ll N^{\varepsilon} \frac{r^2 N^{2} P^4 X^3} {n_1^2 q_1 Q^3} \left(\frac{P T |T'|}{N} + 1 \right). \end{align*} $$
By (5.2) and (6.1), the contribution from
![]() $\Omega _{2}$
to
$\Omega _{2}$
to
![]() $S_{r}^{\pm }(N,X,P) $
is bounded by
$S_{r}^{\pm }(N,X,P) $
is bounded by
 $$ \begin{align*} & \ll N^{\varepsilon} \frac {Q} {r P^2 T^{1/2}|T'|^{1/2} X} \frac{r^{1/2} N X^{3/2}} {Q^{3/2}} \frac{r N P^2 X^{3/2}} { Q^{3/2}} \left(\frac{P^{1/2} T^{1/2}|T'|^{1/2}}{N^{1/2}} + 1 \right) \\ & \ll N^{\varepsilon} \frac {r^{1/2} N^{3/2} } { Q^{3/2} } + N^{\varepsilon} \frac {r^{1/2} N^2 } { Q^{2} T^{1/2}|T'|^{1/2}}. \end{align*} $$
$$ \begin{align*} & \ll N^{\varepsilon} \frac {Q} {r P^2 T^{1/2}|T'|^{1/2} X} \frac{r^{1/2} N X^{3/2}} {Q^{3/2}} \frac{r N P^2 X^{3/2}} { Q^{3/2}} \left(\frac{P^{1/2} T^{1/2}|T'|^{1/2}}{N^{1/2}} + 1 \right) \\ & \ll N^{\varepsilon} \frac {r^{1/2} N^{3/2} } { Q^{3/2} } + N^{\varepsilon} \frac {r^{1/2} N^2 } { Q^{2} T^{1/2}|T'|^{1/2}}. \end{align*} $$
Here, we have used
![]() $P\leq Q$
and
$P\leq Q$
and
![]() $X\ll T^{\varepsilon }$
. By
$X\ll T^{\varepsilon }$
. By
![]() $Q=\frac { N^{1/2}}{K^{1/2}}$
and
$Q=\frac { N^{1/2}}{K^{1/2}}$
and
![]() $N\ll \frac {T^{3/2+\varepsilon } |T'|^{3/2}}{r^2}$
, the above is bounded by
$N\ll \frac {T^{3/2+\varepsilon } |T'|^{3/2}}{r^2}$
, the above is bounded by
8 The nonzero frequencies, II
In this section, we treat the case
![]() $\frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
. By Lemmas 5.1 and 5.3, we get
$\frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
. By Lemmas 5.1 and 5.3, we get
![]() $\Omega _{\neq } \ll N^{\varepsilon } \Omega _3$
, where
$\Omega _{\neq } \ll N^{\varepsilon } \Omega _3$
, where
 $$ \begin{align*} & \Omega_{3} = \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} \sum_{\substack{m\geq1 \\ m\asymp M}} \sum_{\substack{q_2^{\prime}\sim P/q_1 \\ (q_2^{\prime},n_1r)=1}} \sum_{\substack{m'\geq1 \\ m'\asymp M}} |c_{m'}|^2 \; \frac{rq_1}{n_1} \sum_{d_1\mid q_1} \sum_{d_1^{\prime}\mid q_1} d_1^{\prime} (d_1,n_1) \delta_{(d_1,n_1)\mid m}\\ &\qquad\quad \cdot \mathop{\sum\sum}_{\substack{d_2 \mid (q_2, \pm n_1 q_2^{\prime}\pm_1 mn) \\ d_2^{\prime} \mid (q_2^{\prime}, \mp n_1 q_2 \pm_1 m'n)}} d_2d_2^{\prime} \min\left\{\frac{q_2}{[q_2/(q_2,q_2^{\prime}),d_2]},\frac{q_2^{\prime}}{[q_2^{\prime}/(q_2,q_2^{\prime}),d_2^{\prime}]} \right\} \sum_{\substack{ 1\ll |n|\ll \frac{P Q^2 n_1}{q_1 NX^2} N^{\varepsilon} \\ (q_2,q_2^{\prime})\mid n } } N_2. \end{align*} $$
$$ \begin{align*} & \Omega_{3} = \sum_{\substack{q_2\sim P/q_1 \\ (q_2,n_1r)=1}} \sum_{\substack{m\geq1 \\ m\asymp M}} \sum_{\substack{q_2^{\prime}\sim P/q_1 \\ (q_2^{\prime},n_1r)=1}} \sum_{\substack{m'\geq1 \\ m'\asymp M}} |c_{m'}|^2 \; \frac{rq_1}{n_1} \sum_{d_1\mid q_1} \sum_{d_1^{\prime}\mid q_1} d_1^{\prime} (d_1,n_1) \delta_{(d_1,n_1)\mid m}\\ &\qquad\quad \cdot \mathop{\sum\sum}_{\substack{d_2 \mid (q_2, \pm n_1 q_2^{\prime}\pm_1 mn) \\ d_2^{\prime} \mid (q_2^{\prime}, \mp n_1 q_2 \pm_1 m'n)}} d_2d_2^{\prime} \min\left\{\frac{q_2}{[q_2/(q_2,q_2^{\prime}),d_2]},\frac{q_2^{\prime}}{[q_2^{\prime}/(q_2,q_2^{\prime}),d_2^{\prime}]} \right\} \sum_{\substack{ 1\ll |n|\ll \frac{P Q^2 n_1}{q_1 NX^2} N^{\varepsilon} \\ (q_2,q_2^{\prime})\mid n } } N_2. \end{align*} $$
Here, we have used
![]() $|c_{m} c_{m'}| \leq |c_{m}|^2 + |c_{m'}|^2$
and without loss of generality only give details for the case with
$|c_{m} c_{m'}| \leq |c_{m}|^2 + |c_{m'}|^2$
and without loss of generality only give details for the case with
![]() $|c_{m'}|^2$
. By the same arguments as in Section 7, we have
$|c_{m'}|^2$
. By the same arguments as in Section 7, we have
where
 $$ \begin{align*} \Omega_{31}\ &= N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3\mid q_3}d_3 \sum_{d_2 \ll P/q_1q_3} d_2\sum_{\substack{q_2\sim P/q_1q_3 \\ (q_2,n_1r)=1 \\ d_2\mid q_2}} \frac{(q_2/d_2,d_3)}{d_3} \sum_{\substack{m'\asymp M }} |c_{m'}|^2 \\ &\qquad\cdot \sum_{\substack{|n|\ll \frac{P Q^2 n_1}{q_1 NX^2} N^{\varepsilon} \\ q_3\mid n \\ \mp n_1 q_2q_3 \pm_1 m'n \neq 0}} \left( \frac{M}{ q_1}\frac{(d_2d_3,n)}{d_2d_3} + 1\right) \sum_{d_3^{\prime}\mid q_3} d_3^{\prime} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 \\ \mp n_1 q_2q_3 \pm_1 m'n \equiv 0 \bmod d_2^{\prime}d_3^{\prime} }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3 \\ d_2^{\prime} \mid q_2^{\prime}}}1 \end{align*} $$
$$ \begin{align*} \Omega_{31}\ &= N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3\mid q_3}d_3 \sum_{d_2 \ll P/q_1q_3} d_2\sum_{\substack{q_2\sim P/q_1q_3 \\ (q_2,n_1r)=1 \\ d_2\mid q_2}} \frac{(q_2/d_2,d_3)}{d_3} \sum_{\substack{m'\asymp M }} |c_{m'}|^2 \\ &\qquad\cdot \sum_{\substack{|n|\ll \frac{P Q^2 n_1}{q_1 NX^2} N^{\varepsilon} \\ q_3\mid n \\ \mp n_1 q_2q_3 \pm_1 m'n \neq 0}} \left( \frac{M}{ q_1}\frac{(d_2d_3,n)}{d_2d_3} + 1\right) \sum_{d_3^{\prime}\mid q_3} d_3^{\prime} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 \\ \mp n_1 q_2q_3 \pm_1 m'n \equiv 0 \bmod d_2^{\prime}d_3^{\prime} }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3 \\ d_2^{\prime} \mid q_2^{\prime}}}1 \end{align*} $$
and
 $$ \begin{align*} \Omega_{32}\ & = N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3^{\prime}\mid q_3} d_3^{\prime} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3 \\ d_2^{\prime} \mid q_2^{\prime}}} \frac{(q_2^{\prime}/d_2^{\prime},d_3^{\prime})}{d_3^{\prime}} \sum_{\substack{m'\asymp M }} |c_{m'}|^2 \\ &\qquad\cdot \sum_{\substack{|n|\ll \frac{P Q^2 n_1}{q_1 NX^2} N^{\varepsilon} \\ q_3\mid n \\ \mp n_1 q_2q_3 \pm_1 m'n =0}} \sum_{d_3\mid q_3}d_3 \sum_{\substack{d_2 \ll P/q_1q_3 \\ (d_2,\frac{n}{d_3}) \mid \frac{q_3}{d_3} }} d_2 \left( \frac{M}{ q_1}\frac{(d_2,n/d_3)}{d_2} + 1\right) \sum_{\substack{q_2\sim P/q_1q_3 \\ (q_2,n_1r)=1 \\ d_2\mid q_2}} 1. \end{align*} $$
$$ \begin{align*} \Omega_{32}\ & = N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3^{\prime}\mid q_3} d_3^{\prime} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3 \\ d_2^{\prime} \mid q_2^{\prime}}} \frac{(q_2^{\prime}/d_2^{\prime},d_3^{\prime})}{d_3^{\prime}} \sum_{\substack{m'\asymp M }} |c_{m'}|^2 \\ &\qquad\cdot \sum_{\substack{|n|\ll \frac{P Q^2 n_1}{q_1 NX^2} N^{\varepsilon} \\ q_3\mid n \\ \mp n_1 q_2q_3 \pm_1 m'n =0}} \sum_{d_3\mid q_3}d_3 \sum_{\substack{d_2 \ll P/q_1q_3 \\ (d_2,\frac{n}{d_3}) \mid \frac{q_3}{d_3} }} d_2 \left( \frac{M}{ q_1}\frac{(d_2,n/d_3)}{d_2} + 1\right) \sum_{\substack{q_2\sim P/q_1q_3 \\ (q_2,n_1r)=1 \\ d_2\mid q_2}} 1. \end{align*} $$
8.1 The nonzero cases
If
![]() $\mp n_1 q_2 q_3 \pm _1 m'n \neq 0$
, then by (7.5), we have
$\mp n_1 q_2 q_3 \pm _1 m'n \neq 0$
, then by (7.5), we have
 $$ \begin{align*} \Omega_{31}\ &\ll N^{\varepsilon} N_2 \frac{rq_1^3}{n_1} \frac{P}{q_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3\mid q_3} \sum_{d_2 \ll P/q_1q_3} d_2\sum_{\substack{q_2\sim P/q_1q_3 \\ (q_2,n_1r)=1 \\ d_2\mid q_2}} (q_2/d_2,d_3) \\ &\quad\cdot \sum_{\substack{|n|\ll \frac{P Q^2 n_1}{q_1 NX^2} N^{\varepsilon} \\ q_3\mid n}} \left(\frac{M}{q_1}\frac{(d_2d_3,n)}{d_2d_3} + 1\right) \sum_{\substack{m'\asymp M}} |c_{m'}|^2. \end{align*} $$
$$ \begin{align*} \Omega_{31}\ &\ll N^{\varepsilon} N_2 \frac{rq_1^3}{n_1} \frac{P}{q_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3\mid q_3} \sum_{d_2 \ll P/q_1q_3} d_2\sum_{\substack{q_2\sim P/q_1q_3 \\ (q_2,n_1r)=1 \\ d_2\mid q_2}} (q_2/d_2,d_3) \\ &\quad\cdot \sum_{\substack{|n|\ll \frac{P Q^2 n_1}{q_1 NX^2} N^{\varepsilon} \\ q_3\mid n}} \left(\frac{M}{q_1}\frac{(d_2d_3,n)}{d_2d_3} + 1\right) \sum_{\substack{m'\asymp M}} |c_{m'}|^2. \end{align*} $$
 $$ \begin{align*} \Omega_{31} & \ll N^{\varepsilon} N_2 \frac{rq_1^3}{n_1} \frac{P}{q_1} \frac{P Q^2 n_1}{q_1 NX^2} M \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} \sum_{d_3\mid q_3} \sum_{d_2 \ll P/q_1q_3} d_2 \sum_{\substack{q_2\sim P/q_1q_3 \\ (q_2,n_1r)=1 \\ d_2\mid q_2}} (q_2/d_2,d_3) \left(\frac{M}{q_1}\frac{ (d_2,q_3) }{d_2} + 1\right) \\ & \ll N^{\varepsilon} N_2 \frac{rq_1^3}{n_1} \frac{P}{q_1} \frac{P Q^2 n_1}{q_1 NX^2} M \left(\frac{M}{q_1}\frac{P}{q_1} + \frac{P^2}{q_1^2} \right). \end{align*} $$
$$ \begin{align*} \Omega_{31} & \ll N^{\varepsilon} N_2 \frac{rq_1^3}{n_1} \frac{P}{q_1} \frac{P Q^2 n_1}{q_1 NX^2} M \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} \sum_{d_3\mid q_3} \sum_{d_2 \ll P/q_1q_3} d_2 \sum_{\substack{q_2\sim P/q_1q_3 \\ (q_2,n_1r)=1 \\ d_2\mid q_2}} (q_2/d_2,d_3) \left(\frac{M}{q_1}\frac{ (d_2,q_3) }{d_2} + 1\right) \\ & \ll N^{\varepsilon} N_2 \frac{rq_1^3}{n_1} \frac{P}{q_1} \frac{P Q^2 n_1}{q_1 NX^2} M \left(\frac{M}{q_1}\frac{P}{q_1} + \frac{P^2}{q_1^2} \right). \end{align*} $$
Recall that
![]() $N_2 = \frac {r N^{2}X^3} {n_1^2 Q^3} $
. We obtain
$N_2 = \frac {r N^{2}X^3} {n_1^2 Q^3} $
. We obtain
 $$ \begin{align} \Omega_{31} \ll N^{\varepsilon} \frac{r N^{2}X^3} {n_1^2 Q^3} \frac{rq_1^3}{n_1} \frac{P}{q_1} \frac{P Q^2 n_1}{q_1 NX^2} M \left(\frac{M}{q_1}\frac{P}{q_1} + \frac{P^2}{q_1^2} \right) \ll N^{\varepsilon} \frac{r^2 N P^2 X}{n_1^2 q_1 Q } M \left( M P + P^2 \right). \end{align} $$
$$ \begin{align} \Omega_{31} \ll N^{\varepsilon} \frac{r N^{2}X^3} {n_1^2 Q^3} \frac{rq_1^3}{n_1} \frac{P}{q_1} \frac{P Q^2 n_1}{q_1 NX^2} M \left(\frac{M}{q_1}\frac{P}{q_1} + \frac{P^2}{q_1^2} \right) \ll N^{\varepsilon} \frac{r^2 N P^2 X}{n_1^2 q_1 Q } M \left( M P + P^2 \right). \end{align} $$
By (5.2) and (6.1), the contribution from
![]() $\Omega _{31}$
to
$\Omega _{31}$
to
![]() $S_{r}^{\pm }(N,X,P,M) $
is bounded by
$S_{r}^{\pm }(N,X,P,M) $
is bounded by
 $$ \begin{align*} & \ll N^{\varepsilon} \frac{ Q }{r N^{1/2} P X M^{1/2} } \frac{r^{1/2} N X^{3/2}} {Q^{3/2}} \left( \frac{r N^{1/2} P X^{1/2}}{Q^{1/2}} M^{1/2} \left( \frac{PT}{N^{1/2}}P^{1/2} + \frac{N^{1/2}X}{Q} P^{1/2} + P \right) \right) \\ & \ll N^{\varepsilon} \frac{ r^{1/2} N^{1/2} TP^{3/2} }{ Q } + N^{\varepsilon} \frac{ r^{1/2} N^{3/2} P^{1/2} }{ Q^2 } + N^{\varepsilon}\frac{ r^{1/2} N }{ Q } P. \end{align*} $$
$$ \begin{align*} & \ll N^{\varepsilon} \frac{ Q }{r N^{1/2} P X M^{1/2} } \frac{r^{1/2} N X^{3/2}} {Q^{3/2}} \left( \frac{r N^{1/2} P X^{1/2}}{Q^{1/2}} M^{1/2} \left( \frac{PT}{N^{1/2}}P^{1/2} + \frac{N^{1/2}X}{Q} P^{1/2} + P \right) \right) \\ & \ll N^{\varepsilon} \frac{ r^{1/2} N^{1/2} TP^{3/2} }{ Q } + N^{\varepsilon} \frac{ r^{1/2} N^{3/2} P^{1/2} }{ Q^2 } + N^{\varepsilon}\frac{ r^{1/2} N }{ Q } P. \end{align*} $$
Here, we have used
![]() $X\ll T^{\varepsilon }$
and
$X\ll T^{\varepsilon }$
and
![]() $M\ll \frac {P^2T^2}{N}+\frac {NX^2}{Q^2}$
as in (4.10). Note that by the assumption
$M\ll \frac {P^2T^2}{N}+\frac {NX^2}{Q^2}$
as in (4.10). Note that by the assumption
![]() $\frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
, we have
$\frac {NX}{PQ}\gg |T'|^{1-\varepsilon }$
, we have
![]() $P\ll \frac {N}{Q |T'| } T^{\varepsilon }$
. Together with
$P\ll \frac {N}{Q |T'| } T^{\varepsilon }$
. Together with
![]() $Q=\frac { N^{1/2}}{K^{1/2}}$
and
$Q=\frac { N^{1/2}}{K^{1/2}}$
and
![]() $N\ll \frac {T^{3/2+\varepsilon } |T'|^{3/2}}{r^2}$
, the above is bounded by
$N\ll \frac {T^{3/2+\varepsilon } |T'|^{3/2}}{r^2}$
, the above is bounded by
 $$ \begin{align} & \ll N^{\varepsilon} \frac{ r^{1/2} N^{2} T }{ Q^{5/2} |T'|^{3/2} } + N^{\varepsilon} \frac{ r^{1/2} N^{3/2} }{ Q^{3/2} } + N^{\varepsilon}\frac{ r^{1/2} N^2 }{ Q^2 |T'| } \nonumber \\ & \ll N^{1/2+\varepsilon} \frac{ T^{11/8} K^{5/4} }{|T'|^{9/8}} + N^{1/2+\varepsilon} T^{3/8}|T'|^{3/8} K^{3/4} + N^{1/2+\varepsilon} \frac{ T^{3/4} K}{|T'|^{1/4}}. \end{align} $$
$$ \begin{align} & \ll N^{\varepsilon} \frac{ r^{1/2} N^{2} T }{ Q^{5/2} |T'|^{3/2} } + N^{\varepsilon} \frac{ r^{1/2} N^{3/2} }{ Q^{3/2} } + N^{\varepsilon}\frac{ r^{1/2} N^2 }{ Q^2 |T'| } \nonumber \\ & \ll N^{1/2+\varepsilon} \frac{ T^{11/8} K^{5/4} }{|T'|^{9/8}} + N^{1/2+\varepsilon} T^{3/8}|T'|^{3/8} K^{3/4} + N^{1/2+\varepsilon} \frac{ T^{3/4} K}{|T'|^{1/4}}. \end{align} $$
8.2 The zero case
In
![]() $\Omega _{32}$
, we should consider the sums over
$\Omega _{32}$
, we should consider the sums over
![]() $d_2,\ d_3, \ q_2$
first. Since
$d_2,\ d_3, \ q_2$
first. Since
![]() $d_2\mid q_2$
, we rewrite
$d_2\mid q_2$
, we rewrite
![]() $q_2$
as
$q_2$
as
![]() $d_2 q_2$
. Hence, we have
$d_2 q_2$
. Hence, we have
 $$ \begin{align*} \Omega_{32}\ &\ll N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3^{\prime}\mid q_3} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3 \\ d_2^{\prime} \mid q_2^{\prime}}} (q_2^{\prime}/d_2^{\prime},d_3^{\prime}) \sum_{\substack{m'\asymp M }} |c_{m'}|^2 \\ &\quad \cdot \sum_{\substack{1 \ll |n|\ll \frac{P Q^2 n_1}{q_1 NX^2} N^{\varepsilon} \\ q_3\mid n}} \sum_{d_3\mid q_3} \sum_{d_2 \ll P/q_1q_3} \left(\frac{M}{q_1} \Big(d_2,\frac{n}{d_3}\Big)d_3 + d_3 d_2 \right) \sum_{\substack{q_2\sim P/q_1q_3d_2 \\ \mp n_1 d_2 q_2q_3 \pm_1 m'n =0 } } 1. \end{align*} $$
$$ \begin{align*} \Omega_{32}\ &\ll N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} q_3 \sum_{d_3^{\prime}\mid q_3} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3 \\ d_2^{\prime} \mid q_2^{\prime}}} (q_2^{\prime}/d_2^{\prime},d_3^{\prime}) \sum_{\substack{m'\asymp M }} |c_{m'}|^2 \\ &\quad \cdot \sum_{\substack{1 \ll |n|\ll \frac{P Q^2 n_1}{q_1 NX^2} N^{\varepsilon} \\ q_3\mid n}} \sum_{d_3\mid q_3} \sum_{d_2 \ll P/q_1q_3} \left(\frac{M}{q_1} \Big(d_2,\frac{n}{d_3}\Big)d_3 + d_3 d_2 \right) \sum_{\substack{q_2\sim P/q_1q_3d_2 \\ \mp n_1 d_2 q_2q_3 \pm_1 m'n =0 } } 1. \end{align*} $$
Note that
![]() $d_2d_3\leq d_2q_3\ll P/q_1$
and the choices of
$d_2d_3\leq d_2q_3\ll P/q_1$
and the choices of
![]() $(d_2,d_3,q_2)$
are at most
$(d_2,d_3,q_2)$
are at most
![]() $N^{\varepsilon }$
for each fixed
$N^{\varepsilon }$
for each fixed
![]() $m',n$
as
$m',n$
as
![]() $d_2 d_3 q_2 \mid d_2 q_2q_3 \mid m'n$
. Note that
$d_2 d_3 q_2 \mid d_2 q_2q_3 \mid m'n$
. Note that
![]() $(d_2,\frac {n}{d_3}) \mid \frac {q_3}{d_3} $
implies
$(d_2,\frac {n}{d_3}) \mid \frac {q_3}{d_3} $
implies
![]() $(d_2,n/d_3) d_3 \leq q_3$
. Hence
$(d_2,n/d_3) d_3 \leq q_3$
. Hence
 $$ \begin{align*} \Omega_{32} \ll N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} \sum_{d_3^{\prime}\mid q_3} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3d_2^{\prime} }} (q_2^{\prime},d_3^{\prime}) q_3 \sum_{\substack{1 \ll |n|\ll\frac{P Q^2 n_1}{q_1 NX^2} N^{\varepsilon} \\ q_3\mid n}} \!\!\kern-2pt\left(\frac{M}{q_1} q_3 + \frac{P}{q_1} \right) \kern-2pt\!\sum_{\substack{m'\asymp M}} \kern-1pt|c_{m'}|^2\kern-1pt. \end{align*} $$
$$ \begin{align*} \Omega_{32} \ll N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} \sum_{d_3^{\prime}\mid q_3} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3d_2^{\prime} }} (q_2^{\prime},d_3^{\prime}) q_3 \sum_{\substack{1 \ll |n|\ll\frac{P Q^2 n_1}{q_1 NX^2} N^{\varepsilon} \\ q_3\mid n}} \!\!\kern-2pt\left(\frac{M}{q_1} q_3 + \frac{P}{q_1} \right) \kern-2pt\!\sum_{\substack{m'\asymp M}} \kern-1pt|c_{m'}|^2\kern-1pt. \end{align*} $$
By (5.1), we have
 $$ \begin{align*} \Omega_{32} & \ll N^{\varepsilon} N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} \sum_{d_3^{\prime}\mid q_3} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3d_2^{\prime} }} (q_2^{\prime},d_3^{\prime}) \frac{P Q^2 n_1}{q_1 NX^2} \left(\frac{M}{q_1} q_3 + \frac{P}{q_1} \right)M \\ & \ll N^{\varepsilon} \frac{r^2 N P^3 X } {n_1^2 q_1 Q} M \left( M + P \right). \end{align*} $$
$$ \begin{align*} \Omega_{32} & \ll N^{\varepsilon} N_2 \frac{rq_1^3}{n_1} \sum_{\substack{q_3\ll P/q_1 \\ (q_3,n_1r)=1}} \sum_{d_3^{\prime}\mid q_3} \sum_{\substack{d_2^{\prime} \ll P/q_1q_3 }} d_2^{\prime} \sum_{\substack{q_2^{\prime}\sim P/q_1q_3d_2^{\prime} }} (q_2^{\prime},d_3^{\prime}) \frac{P Q^2 n_1}{q_1 NX^2} \left(\frac{M}{q_1} q_3 + \frac{P}{q_1} \right)M \\ & \ll N^{\varepsilon} \frac{r^2 N P^3 X } {n_1^2 q_1 Q} M \left( M + P \right). \end{align*} $$
Note that this bound is the same as the bound for
![]() $\Omega _{31}$
in (8.2). Hence, we get the same bound for the contribution from
$\Omega _{31}$
in (8.2). Hence, we get the same bound for the contribution from
![]() $\Omega _{32}$
to
$\Omega _{32}$
to
![]() $S_{r}^{\pm }(N,X,P,M) $
.
$S_{r}^{\pm }(N,X,P,M) $
.
9 Proof of Theorem 1.1
By (6.2) and (6.3), we have the contribution from the zero frequency to
![]() $S_{r}^{\pm }(N,X,P) $
is bounded by
$S_{r}^{\pm }(N,X,P) $
is bounded by
 $$ \begin{align*} \ll N^{1/2+\varepsilon} \left( \frac{ r^{1/2} K^{3/2} T}{ |T'| } + r^{1/2} T^{1/2} |T'|^{1/2} + T^{3/8} |T'|^{3/8} K^{3/4} \right). \end{align*} $$
$$ \begin{align*} \ll N^{1/2+\varepsilon} \left( \frac{ r^{1/2} K^{3/2} T}{ |T'| } + r^{1/2} T^{1/2} |T'|^{1/2} + T^{3/8} |T'|^{3/8} K^{3/4} \right). \end{align*} $$
By (7.7), (7.8), (7.9), and (8.3), we have the contribution from the nonzero frequencies to
![]() $S_{r}^{\pm }(N,X,P) $
is bounded by
$S_{r}^{\pm }(N,X,P) $
is bounded by
 $$ \begin{align*} &\ll N^{1/2+\varepsilon} \bigg( \frac{ T^{7/8} |T'|^{7/8}}{K^{1/2}} + \frac{ T^{3/4} |T'|^{3/4}}{K^{1/4}} + T^{5/8}|T'|^{5/8} + T^{1/2}|T'|^{1/2} K^{1/4} \\ &\qquad\qquad\qquad + \frac{K^{3/4} T^{7/8}}{|T'|^{1/8}} + T^{3/8}|T'|^{3/8} K^{3/4} + \frac{T^{3/4} K} { |T'|^{1/4}} + T^{1/4}|T'|^{1/4} K + \frac{ T^{11/8} K^{5/4} }{|T'|^{9/8}} \bigg). \end{align*} $$
$$ \begin{align*} &\ll N^{1/2+\varepsilon} \bigg( \frac{ T^{7/8} |T'|^{7/8}}{K^{1/2}} + \frac{ T^{3/4} |T'|^{3/4}}{K^{1/4}} + T^{5/8}|T'|^{5/8} + T^{1/2}|T'|^{1/2} K^{1/4} \\ &\qquad\qquad\qquad + \frac{K^{3/4} T^{7/8}}{|T'|^{1/8}} + T^{3/8}|T'|^{3/8} K^{3/4} + \frac{T^{3/4} K} { |T'|^{1/4}} + T^{1/4}|T'|^{1/4} K + \frac{ T^{11/8} K^{5/4} }{|T'|^{9/8}} \bigg). \end{align*} $$
Assume
![]() $K\leq T^{1/2}|T'|^{1/2}$
. Note that
$K\leq T^{1/2}|T'|^{1/2}$
. Note that
![]() $T'\ll T$
. Hence, we have
$T'\ll T$
. Hence, we have
 $$ \begin{align*} S_{r}^{\pm}(N,X,P) \ll N^{1/2+\varepsilon} \kern-1pt\bigg( \frac{ R^{1/2} K^{3/2} T}{ |T'| } + R^{1/2} T^{1/2} |T'|^{1/2} + \frac{ T^{7/8} |T'|^{7/8}}{K^{1/2}} + \frac{K^{3/4} T^{7/8}}{|T'|^{1/8}} +\frac{ T^{11/8} K^{5/4} }{|T'|^{9/8}} \bigg)\kern-1.2pt. \end{align*} $$
$$ \begin{align*} S_{r}^{\pm}(N,X,P) \ll N^{1/2+\varepsilon} \kern-1pt\bigg( \frac{ R^{1/2} K^{3/2} T}{ |T'| } + R^{1/2} T^{1/2} |T'|^{1/2} + \frac{ T^{7/8} |T'|^{7/8}}{K^{1/2}} + \frac{K^{3/4} T^{7/8}}{|T'|^{1/8}} +\frac{ T^{11/8} K^{5/4} }{|T'|^{9/8}} \bigg)\kern-1.2pt. \end{align*} $$
If
![]() $T'\gg T^{5/6}$
, then we take
$T'\gg T^{5/6}$
, then we take
![]() $K=|T'|^{4/5}$
, and hence by (2.5), we have
$K=|T'|^{4/5}$
, and hence by (2.5), we have
If
![]() $T^{3/5} \ll T'\ll T^{5/6}$
, then we take
$T^{3/5} \ll T'\ll T^{5/6}$
, then we take
![]() $K=|T'|^{8/7}T^{-2/7}$
, and hence by (2.5) we have
$K=|T'|^{8/7}T^{-2/7}$
, and hence by (2.5) we have
Note that K satisfies the condition (4.17). By (3.1) and (4.16), we prove Proposition 2.2, and hence Theorem 1.1.
Acknowledgements
The author would like to thank Professor Valentin Blomer and Professor Philippe Michel for their help and encouragement. He also wants to thank the referees for their very helpful comments and suggestions. This work was supported by the National Key R&D Program of China (No. 2021YFA1000700) and NSFC (Nos. 12001314 and 12031008).
Competing interests
The authors have no competing interest to declare.