Published online by Cambridge University Press: 12 March 2014
We prove the undecidability of a very large class of restricted and unrestricted wreath products (Theorem 1.2), and of some skew fields of power series (Section2). Both undecidabilities are obtained by interpreting some enrichments of twisted wreath products, which are themselves proved to be undecidable (Proposition 1.1).
We consider division rings of power series in various languages:
We show (Theorem 2.8) that every power series division ring k((B)), whose field of constants k is commutative and whose ordered group of exponents is noncommutative with a convex center, is undecidable in every extension of the language of rings where the valuation and the ordered group B are definable.
For certain k and B we prove here the undecidability of the structure
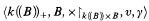
where X↾k((B))xB is the restriction of the multiplication to k((B)) Χ B,and γ is a given conjugation of k((B)). This shows that we cannot hope to improve our previous result, a sort of Ax-Kochen-Ershov principle for power series division rings, which ensures that
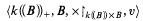
is decidable for every decidable solvable B.