Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Montalbán, Antonio
2017.
Computability and Complexity.
Vol. 10010,
Issue. ,
p.
221.
Bazhenov, N. A.
and
Harrison-Trainor, M.
2019.
Constructing Decidable Graphs from Decidable Structures.
Algebra and Logic,
Vol. 58,
Issue. 5,
p.
369.
Harrison-Trainor, Matthew
and
Ho, Meng-Che “Turbo”
2021.
Finitely generated groups are universal among finitely generated structures.
Annals of Pure and Applied Logic,
Vol. 172,
Issue. 1,
p.
102855.
Montalbán, Antonio
2021.
Computable Structure Theory.
ANDREWS, URI
KNIGHT, JULIA F.
KUYPER, RUTGER
MILLER, JOSEPH S.
and
SOSKOVA, MARIYA I.
2023.
EXPANDING THE REALS BY CONTINUOUS FUNCTIONS ADDS NO COMPUTATIONAL POWER.
The Journal of Symbolic Logic,
Vol. 88,
Issue. 3,
p.
1083.


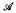 such that
such that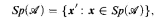
 is the set of Turing degrees which compute a copy of
is the set of Turing degrees which compute a copy of 