Since A. Robinson introduced the classes of existentially complete and generic models, conditions which were interesting for elementary classes were considered for these classes. In [6] H. Simmons showed that with the natural definitions there are prime and saturated existentially complete models and these are very similar to their elementary counterparts which were introduced by Vaught [2, 2.3]. As Example 6 will show, there is a limit to the similarity—there are theories which have exactly two existentially complete models.

In [6] H. Simmons considers the following list of properties, shows that each property implies the next one and asks whether any of them implies the previous one:

1.1. T is ℵ0-categorical.

1.2. T has an ℵ0-categorical model companion.

1.3. ∣E∣ = 1.

1.4. ∣E∣ < .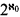

1.5. T has a countable ∃-saturated model.

1.6. T has a ∃-prime model.

1.7. Each universal formula is implied by a ∃-atomic existential formula.

[The reader is referred to [1], [3], [4] and [6] for the definitions and background.

We only mention that T is always a countable theory. All the models under discussion are countable. Thus E is the class of countable existentially complete models and F and G, respectively, are the classes of countable finite and infinite generic models. For every class C,∣C∣ is the number of (countable) models in C.]