Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-22T20:48:30.435Z Has data issue: false hasContentIssue false
  • English
  • Français

Adding dominating reals with ωω of bounding posets

Published online by Cambridge University Press:  12 March 2014

Janusz Pawlikowski
Janusz Pawlikowski*
Affiliation:
Instytut Matematyczny, Uniwersytet Wrogławski, 50-384 Wrocław, Poland
Get access Rights & Permissions [Opens in a new window]

Extract

Let B be the random real forcing. Miller [Mi] asked if there are ZFC models M ⊆ N such that forcing with BM over N adds a dominating real. A YES answer was provided by Judah and Shelah in [JS], where in a long and sophisticated construction they built such models. In this paper we prove that forcing with BV over VI, where I is the infinitely often equal real forcing of [Mi], adds a dominating real over VI. This greatly simplifies the YES answer to Miller's question. Moreover it turns out that B may be replaced here by E, the eventually different real forcing of [Mi]. This answers the second part of Miller's question. We also prove that both side by side products I × B and I × E add a Hechler dominating real over V.

In this section we establish the main result of the paper; namely, we prove that forcing over VI with either of the posets BV or EV adds a dominating real over VI.

First we recall the definitions of I and E from [Mi]. The infinitely often equal real forcing is the set

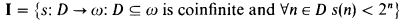
ordered by extension. Miller [Mi] proves that I is ωω bounding.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 57 , Issue 2 , June 1992 , pp. 540 - 547
Copyright
Copyright © Association for Symbolic Logic 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[G]Grigorieff, S., Combinatorics on ideals and forcing, Annals of Mathematical Logic, vol. 3 (1971), pp. 363–394.CrossRefGoogle Scholar
[H]Hechler, S. H., On the existence of certain cofinal subsets in ω ω, Axiomatic set theory, Proceedings of Symposia in Pure Mathematics, vol. 13, part 2, American Mathematical Society, Providence, Rhode Island, 1974, pp. 155–174.CrossRefGoogle Scholar
[JS]Judah, H. and Shelah, S., Adding dominating reals with random algebra, preprint.Google Scholar
[Ma]Mathias, A. R. D., Happy families, Annals of Mathematical Logic, vol. 12 (1977), pp. 59–111.CrossRefGoogle Scholar
[Mi]Miller, A., Some properties of measure and category, Transactions of the American Mathematical Society, vol. 266 (1981), pp. 93–114; Corrections and additions, Transactions of the American Mathematical Society., vol. 271 (1982), pp. 347–348.CrossRefGoogle Scholar
[T]Truss, J. K., Sets having calibre ℵ1, Logic colloquium '76 (Gandy, R. O. and Hyland, J. M. E., editors), North-Holland, Amsterdam, 1977, pp. 595–612.Google Scholar