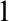 $_1$ THEORIES
$_1$ THEORIESPublished online by Cambridge University Press: 11 June 2021
We study the notion of weak canonical bases in an NSOP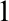 $_{1}$
theory T with existence. Given
$_{1}$
theory T with existence. Given 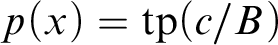 $p(x)=\operatorname {tp}(c/B)$
where
$p(x)=\operatorname {tp}(c/B)$
where 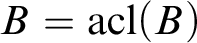 $B=\operatorname {acl}(B)$
in
$B=\operatorname {acl}(B)$
in 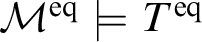 ${\mathcal M}^{\operatorname {eq}}\models T^{\operatorname {eq}}$
, the weak canonical base of p is the smallest algebraically closed subset of B over which p does not Kim-fork. With this aim we firstly show that the transitive closure
${\mathcal M}^{\operatorname {eq}}\models T^{\operatorname {eq}}$
, the weak canonical base of p is the smallest algebraically closed subset of B over which p does not Kim-fork. With this aim we firstly show that the transitive closure  $\approx $
of collinearity of an indiscernible sequence is type-definable. Secondly, we prove that given a total
$\approx $
of collinearity of an indiscernible sequence is type-definable. Secondly, we prove that given a total 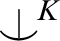 $\mathop {\smile \hskip -0.9em ^| \ }^K$
-Morley sequence I in p, the weak canonical base of
$\mathop {\smile \hskip -0.9em ^| \ }^K$
-Morley sequence I in p, the weak canonical base of 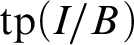 $\operatorname {tp}(I/B)$
is
$\operatorname {tp}(I/B)$
is 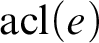 $\operatorname {acl}(e)$
, if the hyperimaginary
$\operatorname {acl}(e)$
, if the hyperimaginary 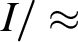 $I/\approx $
is eliminable to e, a sequence of imaginaries. We also supply a couple of criteria for when the weak canonical base of p exists. In particular the weak canonical base of p is (if exists) the intersection of the weak canonical bases of all total
$I/\approx $
is eliminable to e, a sequence of imaginaries. We also supply a couple of criteria for when the weak canonical base of p exists. In particular the weak canonical base of p is (if exists) the intersection of the weak canonical bases of all total 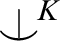 $\mathop {\smile \hskip -0.9em ^| \ }^K$
-Morley sequences in p over B. However, while we investigate some examples, we point out that given two weak canonical bases of total
$\mathop {\smile \hskip -0.9em ^| \ }^K$
-Morley sequences in p over B. However, while we investigate some examples, we point out that given two weak canonical bases of total 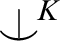 $\mathop {\smile \hskip -0.9em ^| \ }^K$
-Morley sequences in p need not be interalgebraic, contrary to the case of simple theories. Lastly we suggest an independence relation relying on weak canonical bases, when T has those. The relation, satisfying transitivity and base monotonicity, might be useful in further studies on NSOP
$\mathop {\smile \hskip -0.9em ^| \ }^K$
-Morley sequences in p need not be interalgebraic, contrary to the case of simple theories. Lastly we suggest an independence relation relying on weak canonical bases, when T has those. The relation, satisfying transitivity and base monotonicity, might be useful in further studies on NSOP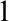 $_1$
theories .
$_1$
theories .