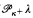Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T16:12:16.919Z Has data issue: false hasContentIssue false
  • English
  • Français

κ-stationary subsets of , infinitary games, and distributive laws in Boolean algebras

Published online by Cambridge University Press:  12 March 2014

Natasha Dobrinen
Natasha Dobrinen*
Affiliation:
Department of Mathematics, University of Denver, Denver, CO 80208, USA, E-mail: [email protected], URL: http://www.math.du.edu/dobrinen/
Get access Rights & Permissions [Opens in a new window]

Abstract

We characterize the (κ, λ, < μ)-distributive law in Boolean algebras in terms of cut and choose games 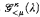, when μ ≤ κ ≤ λ and κ<κ = κ. This builds on previous work to yield game-theoretic characterizations of distributive laws for almost all triples of cardinals κ, λ, μ with μ ≤ λ, under GCH. In the case when μ ≤ κ ≤ λ and κ<κ = κ, we show that it is necessary to consider whether the κ-stationarity of 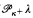in the ground model is preserved by 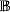. In this vein, we develop the theory of κ-club and κ-stationary subsets of 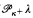. We also construct Boolean algebras in which Player I wins 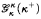but the (κ, ∞, κ)-d.1. holds, and, assuming GCH, construct Boolean algebras in which many games are undetermined.

Keywords

Boolean algebradistributive lawgameκ-stationary set
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 73 , Issue 1 , March 2008 , pp. 238 - 260
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Abraham, Uri and Shelah, Saharon, Forcing closed and unbounded sets, this Journal, vol. 48 (1983), no. 3, pp. 643–657.Google Scholar
[2]Baumgartner, J. E., Harrington, L. A., and Kleinberg, E. M., Adding a closed unbounded set, this Journal, vol. 41 (1976), no. 2, pp. 481–482.Google Scholar
[3]Elizabeth, Θ Brown, , Superperfect forcing at uncountable cardinals, preprint.Google Scholar
[4]Cummings, James and Dobrinen, Natasha, The hyper-weak distributive law and a related game in Boolean algebras, Annals of Pure and Applied Logic, to appear.Google Scholar
[5]Dobrinen, Natasha, Games and general distributive laws in Boolean algebras, Proceedings of the American Mathematical Society, vol. 131 (2003), pp. 309–318.CrossRefGoogle Scholar
[6]Foreman, Matthew and Magidor, Menachem, Large cardinals and definable counterexamples to the continuum hypothesis, Annals of Pure and Applied Logic, vol. 76 (1995), pp. 47–97.CrossRefGoogle Scholar
[7]Gray, Charles, Iterated forcing from the strategic point of view, Ph.D. thesis, University of California, Berkeley, 1983.Google Scholar
[8]Huuskonen, Taneli, Hyttinen, Tapani, and Rautila, Mika, On the κ-club game on λ and i[λ], Archive for Mathematical Logic, vol. 38 (1999), no. 8, pp. 549–557.CrossRefGoogle Scholar
[9]Huuskonen, Taneli, Hyttinen, Tapani, and Rautila, Mika, On potential isomorphism and non-structure, Archive for Mathematical Logic, vol. 43 (2004), no. 1, pp. 85–120.Google Scholar
[10]Jech, Thomas, A game theoretic property of Boolean algebras, Studies in Logic and the Foundations of Mathematics, vol. 96, North-Holland, 1978.Google Scholar
[11]Jech, Thomas, More game-theoretical properties of Boolean algebras, Annals of Pure Applied Logic, vol. 26 (1984), no. 1, pp. 11–29.CrossRefGoogle Scholar
[12]Jech, Thomas, Multiple forcing, Cambridge University Press, 1986.Google Scholar
[13]Jech, Thomas, Set theory, the 3rd millennium ed., Springer, 2003.Google Scholar
[14]Kamburelis, Anastasis, On the weak distributivity game, Annals of Pure Applied Logic, vol. 66 (1994), no. 1, pp. 19–26.CrossRefGoogle Scholar
[15]Kanamori, Akihiro, Perfect-set forcing for uncountable cardinals, Annals of Mathematical Logic, vol. 19 (1980), no. 1-2, pp. 97–114.CrossRefGoogle Scholar
[16]Kanamori, Akihiro, The Higher Infinite, 2nd ed., Springer, 2003.Google Scholar
[17]Koppelberg, Sabine, The general theory of Boolean algebras, Handbook on Boolean algebras, vol. 1, North-Holland, 1989.Google Scholar
[18]Kueker, David W., Löwenheim-Skolem and interpolation theorems in infinitary languages, Bulletin of the American Mathematical Society, vol. 78 (1972), pp. 211–215.CrossRefGoogle Scholar
[19]Kueker, David W., Countable approximations and Löwenheim-Skolem theorems, Annals of Mathematical Logic, vol. 11 (1977), no. 1, pp. 57–103.CrossRefGoogle Scholar
[20]Magidor, Menachem, Representing sets of ordinals as countable unions of sets in the core model, Transactions of the American Mathematical Society, vol. 317 (1990), no. 1, pp. 91–126.CrossRefGoogle Scholar
[21]Matsubara, Yo, Consistency of Menas' conjecure, Journal of the Mathematical Society of Japan, vol. 42 (1990), pp. 259–263.CrossRefGoogle Scholar
[22]Mekler, Alan H. and Shelah, Saharon, Stationary logic and its friends. II, Notre Dame Journal of Formal Logic, vol. 27 (1986), no. 1, pp. 39–50.CrossRefGoogle Scholar
[23]Piper, Gregory, On the combinatorics of P κλ, Ph.D. thesis, University of East Anglia, 2003.Google Scholar
[24]Piper, Gregory, Regular closure and corresponding P κλ versions of ◊ and ♣. preprint.Google Scholar
[25]Piper, Gregory, Regular clubs in Pκλ, preprint.Google Scholar
[26]Zapletal, Jindřich, More on the cut and choose game, Annals of Pure Applied Logic, vol. 76 (1995), pp. 291–301.CrossRefGoogle Scholar