Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
COLE, JOSHUA A.
and
SIMPSON, STEPHEN G.
2007.
MASS PROBLEMS AND HYPERARITHMETICITY.
Journal of Mathematical Logic,
Vol. 07,
Issue. 02,
p.
125.
Barmpalias, George
Lewis, Andrew E.M.
and
Stephan, Frank
2008.
Π10 classes, LR degrees and Turing degrees.
Annals of Pure and Applied Logic,
Vol. 156,
Issue. 1,
p.
21.
BARMPALIAS, GEORGE
and
MORPHETT, ANTHONY
2009.
Non-cupping, measure and computably enumerable splittings.
Mathematical Structures in Computer Science,
Vol. 19,
Issue. 1,
p.
25.
Barmpalias, George
Downey, Rod
and
Greenberg, Noam
2009.
𝐾-trivial degrees and the jump-traceability hierarchy.
Proceedings of the American Mathematical Society,
Vol. 137,
Issue. 6,
p.
2099.
Miller , Joseph S.
2009.
The K-Degrees, Low for K Degrees,and Weakly Low for K Sets.
Notre Dame Journal of Formal Logic,
Vol. 50,
Issue. 4,
Barmpalias, George
2010.
Elementary differences between the degrees of unsolvability and degrees of compressibility.
Annals of Pure and Applied Logic,
Vol. 161,
Issue. 7,
p.
923.
Barmpalias, George
2010.
Relative Randomness and Cardinality.
Notre Dame Journal of Formal Logic,
Vol. 51,
Issue. 2,
Barmpalias, George
and
Lewis, Andrew E. M.
2011.
Chaitin's halting probability and the compression of strings using oracles.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 467,
Issue. 2134,
p.
2912.
Miller, Joseph S.
and
Yu, Liang
2011.
Oscillation in the initial segment complexity of random reals.
Advances in Mathematics,
Vol. 226,
Issue. 6,
p.
4816.
Barmpalias, George
and
Vlek, C.S.
2011.
Kolmogorov complexity of initial segments of sequences and arithmetical definability.
Theoretical Computer Science,
Vol. 412,
Issue. 41,
p.
5656.
Barmpalias, George
Miller, Joseph S.
and
Nies, André
2012.
Randomness notions and partial relativization.
Israel Journal of Mathematics,
Vol. 191,
Issue. 2,
p.
791.
Morphett, A.
2012.
Prompt enumerations and relative randomness.
Journal of Logic and Computation,
Vol. 22,
Issue. 4,
p.
877.
Diamondstone, David
2012.
Low upper bounds in the LR degrees.
Annals of Pure and Applied Logic,
Vol. 163,
Issue. 3,
p.
314.
Bienvenu, Laurent
and
Miller, Joseph S.
2012.
Randomness and lowness notions via open covers.
Annals of Pure and Applied Logic,
Vol. 163,
Issue. 5,
p.
506.
Barmpalias, G.
2012.
Compactness arguments with effectively closed sets for the study of relative randomness.
Journal of Logic and Computation,
Vol. 22,
Issue. 4,
p.
679.
Barmpalias, George
and
Li, Angsheng
2013.
Kolmogorov complexity and computably enumerable sets.
Annals of Pure and Applied Logic,
Vol. 164,
Issue. 12,
p.
1187.
Barmpalias, George
2013.
Algorithmic Randomness and Measures of Complexity.
The Bulletin of Symbolic Logic,
Vol. 19,
Issue. 3,
p.
318.
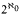 degrees (so that, in particular, there exist LR degrees with uncountably many predecessors) and we give sample results which demonstrate how various techniques from the theory of the c.e. degrees can be used to prove results about the c.e. LR degrees.
degrees (so that, in particular, there exist LR degrees with uncountably many predecessors) and we give sample results which demonstrate how various techniques from the theory of the c.e. degrees can be used to prove results about the c.e. LR degrees.