Published online by Cambridge University Press: 12 March 2014
Let 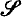 be a finite set of (nonlogical) predicate symbols. By an
be a finite set of (nonlogical) predicate symbols. By an 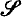 -structure, we mean a relational structure appropriate for
-structure, we mean a relational structure appropriate for 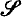 . Let
. Let 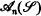 be the set of all
be the set of all 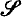 -structures with universe {1, …, n}. For each first-order
-structures with universe {1, …, n}. For each first-order 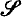 -sentence σ (with equality), let μ
n
(σ) be the fraction of members of
-sentence σ (with equality), let μ
n
(σ) be the fraction of members of 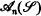 for which σ is true. We show that μ
n
(σ) always converges to 0 or 1 as n → ∞, and that the rate of convergence is geometrically fast. In fact, if T is a certain complete, consistent set of first-order
for which σ is true. We show that μ
n
(σ) always converges to 0 or 1 as n → ∞, and that the rate of convergence is geometrically fast. In fact, if T is a certain complete, consistent set of first-order 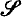 -sentences introduced by H. Gaifman [6], then we show that, for each first-order
-sentences introduced by H. Gaifman [6], then we show that, for each first-order 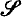 -sentence σ, μ
n
(σ) →
n
1 iff T ⊩ ω. A surprising corollary is that each finite subset of T has a finite model. Following H. Scholz [8], we define the spectrum of a sentence σ to be the set of cardinalities of finite models of σ. Another corollary is that for each first-order
-sentence σ, μ
n
(σ) →
n
1 iff T ⊩ ω. A surprising corollary is that each finite subset of T has a finite model. Following H. Scholz [8], we define the spectrum of a sentence σ to be the set of cardinalities of finite models of σ. Another corollary is that for each first-order 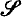 -sentence a, either σ or ˜σ has a cofinite spectrum (in fact, either σ or ˜σ is “nearly always“ true).
-sentence a, either σ or ˜σ has a cofinite spectrum (in fact, either σ or ˜σ is “nearly always“ true).
Let 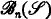 be a subset of
be a subset of 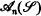 which contains for each
which contains for each 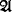 in
in 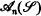 exactly one structure isomorphic to
exactly one structure isomorphic to 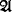 . For each first-order
. For each first-order 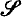 -sentence σ, let ν
n
(σ) be the fraction of members of
-sentence σ, let ν
n
(σ) be the fraction of members of 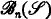 which a is true. By making use of an asymptotic estimate [3] of the cardinality of
which a is true. By making use of an asymptotic estimate [3] of the cardinality of 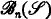 and by our previously mentioned results, we show that v
n(σ) converges as n → ∞, and that lim
n
ν
n
(σ) = lim
n
μ
n
(σ).If
and by our previously mentioned results, we show that v
n(σ) converges as n → ∞, and that lim
n
ν
n
(σ) = lim
n
μ
n
(σ).If 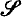 contains at least one predicate symbol which is not unary, then the rate of convergence is geometrically fast.
contains at least one predicate symbol which is not unary, then the rate of convergence is geometrically fast.
The author is grateful to Robert Vaught, William Craig, and Ralph McKenzie for useful suggestions which improved readability.
This paper is based on a part of the author's doctoral dissertation [2] in the Department of Mathematics at the University of California, Berkeley. Part of this work was carried out while the author was a National Science Foundation Graduate Fellow; also, part of this work was supported by NSF grant GP-24532.