Un espace ultramétrique est un ensemble muni d'une distance à valeurs dans un ordre total avec premier élément et pour laquelle tout triangle est isocèle avex deux grands côtés égaux. Les deux cas importants d'espaces ultramétriques sont:

(1) les corps valués lorsqu'on ne considère que leur structure métrique, et

(2) les ensembles Aλ, où λ est un ensemble bien ordonné, munis de la distance d(α, β) = inf {γ ∈ λ; α(γ) ≠ β(γ)} si α ≠ β et d(α, β) = 0 sinon; distance à valeurs dans l'ordre inverse de λ enrichi d'un premier élément 0.

Nous étudions ces structures dans un langage comportant un seul type de variables, les points de l'espace, et un prédicat à quatre places traduisant l'ordre sur les distances

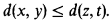
Nous définissons la notion d'espace riche, qui est la modèle-complétion relative à un ensemble des distances fixé: un espace est riche si et seulement s'il est existentiellement clos dans toute extension qui n'ajoute pas de nouvelle distance. Les deux exemples précédemment donnés, espaces Aλ et corps valués, fournissent des espaces riches. La suite de l'article s'attache à la description des espaces riches.