Published online by Cambridge University Press: 15 June 2020
We show in ZFC that the existence of completely separable maximal almost disjoint families of subsets of 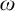 $\omega $
implies that the modal logic
$\omega $
implies that the modal logic 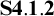 $\mathbf {S4.1.2}$
is complete with respect to the Čech–Stone compactification of the natural numbers, the space
$\mathbf {S4.1.2}$
is complete with respect to the Čech–Stone compactification of the natural numbers, the space 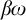 $\beta \omega $
. In the same fashion we prove that the modal logic
$\beta \omega $
. In the same fashion we prove that the modal logic  $\mathbf {S4}$
is complete with respect to the space
$\mathbf {S4}$
is complete with respect to the space 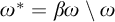 $\omega ^*=\beta \omega \setminus \omega $
. This improves the results of G. Bezhanishvili and J. Harding in [4], where the authors prove these theorems under stronger assumptions (
$\omega ^*=\beta \omega \setminus \omega $
. This improves the results of G. Bezhanishvili and J. Harding in [4], where the authors prove these theorems under stronger assumptions ( $\mathfrak {a=c}$
). Our proof is also somewhat simpler.
$\mathfrak {a=c}$
). Our proof is also somewhat simpler.