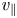1. Introduction
The transport of matter and radiation in the solar wind and terrestrial magnetosphere is a complicated problem involving competing processes of charged particles interacting with electric and magnetic fields. Given the rapid expansion of the solar wind within the Parker spiral, it would be expected that superthermal particles originating in the corona would cool rapidly as a function of the distance to the Sun. However, observations show that this is not the case and superthermal particles have been observed out to the termination shock (Decker et al. Reference Decker, Krimigis, Roelof, Hill, Armstrong, Gloeckler, Hamilton and Lanzerotti2008), suggesting the presence of an additional heating/acceleration mechanism. These superthermal tails have been observed to follow a power-law distribution in velocity space (Fisk & Gloeckler Reference Fisk and Gloeckler2006).
Much of the work on a possible explanation for this additional heating centres on wave–particle interactions as the primary heating mechanism, where energy is provided by the turbulence associated with propagating waves (Kennel & Petschek Reference Kennel and Petschek1966; Ergun et al. Reference Ergun, Larson, Lin, McFadden, Carlson, Anderson, Muschietti, McCarthy, Parks and Reme1998; Vinas, Wong & Klimas Reference Vinas, Wong and Klimas2000; Vocks et al. Reference Vocks, Salem, Lin and Mann2005; Rhee, Ryu & Yoon Reference Rhee, Ryu and Yoon2006; Califano & Mangeney Reference Califano and Mangeney2008). In these models, particles are energized at the resonant velocities, where 
$v k \cos \varTheta \simeq \omega$, and with 
$\cos \varTheta = \boldsymbol {v}\boldsymbol {\cdot }\boldsymbol {k}/(vk)$. Particle energization is then limited to 
$v\leq \omega /(k\cos \varTheta )$. Superthermal electrons then require energization by waves with large phase velocities 
$v_p=\omega /k$, such as whistler waves (Wilson et al. Reference Wilson, Koval, Szabo, Breneman, Cattell, Goetz, Kellogg, Kersten, Kasper and Maruca2012). However, in many systems, the energy available in whistler waves has been found to be insufficient to explain the observed level of electron energization, and in a recent analysis using NASA's Magnetospheric Multiscale (MMS) mission data it was found that while whistlers are effective for pitch angle scattering, the whistler bursts did not correlate well with electron energization (Oka et al. Reference Oka, Wilson III, Phan, Hull, Amano, Hoshino, Argall, Le Contel, Agapitov and Gershman2017).
Another challenge in using wave–particle interactions to explain the heating in the solar wind is the near-ubiquitous observations of power-law distributions of superthermal particles. Such power-law distributions are known to form in Fermi-like heating processes where the energy gains of individual particles are proportional to their initial energies, but it is difficult to reproduce with a set of resonant wave–particle interactions.
Previous work on magnetic pumping (such as transit-time damping (Barnes Reference Barnes1966; Berger et al. Reference Berger, Newcomb, Dawson, Frieman, Kulsrud and Lenard1971; Stix Reference Stix1992; Lichko et al. Reference Lichko, Egedal, Daughton and Kasper2017)), have largely concluded that pumping is not efficient for energizing superthermal electrons with 
$v>\omega /(k \cos \varTheta )$. Meanwhile, the pumping models of Egedal et al. (Reference Egedal, Monkhorst, Lichko and Montag2018) and Lichko & Egedal (Reference Lichko and Egedal2020) include the effects of trapping and differs significantly from earlier results, as the trapping permits especially electrons with 
$v\gg \omega /(k \cos \varTheta )$ to become energized. Another interesting property that is in contrast to the turbulent cascade where the energy is transferred from large scales to small scales before being absorbed (Howes et al. Reference Howes, Dorland, Cowley, Hammett, Quataert, Schekochihin and Tatsuno2008; Sahraoui et al. Reference Sahraoui, Goldstein, Robert and Khotyaintsev2009), in magnetic pumping the energy is provided directly by the energy-rich largest-scale magnetic fluctuations.
The results of the present paper can be considered an extension of the magnetic pumping model by Lichko & Egedal (Reference Lichko and Egedal2020). Here we uncover an additional heating mechanism, which is related to the particular effect of electrons becoming trapped/untrapped in magnetic mirror-structures that form in the presence of compressional wave dynamics. The process leads to parallel energy mixing (or 
$v_{\parallel }$-mixing) yielding a net energy gain also for electrons for which the magnetic moment, 
$\mu$, is conserved. In turn, by adding weak pitch angle scattering to the system, a heating model is obtained similar to that of Lichko & Egedal (Reference Lichko and Egedal2020), with the main difference being enhanced heating rates of superthermal electrons in the limit of weak pitch angle scattering.
The paper is organized as follows. In § 2 we evaluate the parallel electron energization and mixing in a system of magnetic trapping/detrapping where the magnetic moment, 
$\mu$ is consider an adiabatic invariant. In the drift kinetic limit and the limit of fast orbit bounce motion, in § 3 we show how this 
$v_{\parallel }$-mixing leads to parallel diffusion within the trapped part of the electron distributions. In § 4 we add to the model a phenomenological pitch angle scattering and evaluate the net changes to a distribution which after complete 
$v_{\parallel }$-diffusion becomes reisotropized by the pitch angle scattering. We then in § 5 consider a scenario of simultaneous 
$v_{\parallel }$-mixing and pitch angle diffusion, for which we derive an evolution equation for the slowly varying background electron distribution. In § 6 the new results are discussed and the analysis concluded with a comparison with those of Lichko & Egedal (Reference Lichko and Egedal2020), emphasizing enhanced heating rates for low values of pitch angle scattering.
2. Parallel energy mixing
Waves including magnetic perturbations can trap electrons, and considering an idealized standing wave configuration, Lichko & Egedal (Reference Lichko and Egedal2020) demonstrated the importance of trapping to render magnetic pumping an efficient heating mechanism for superthermal electrons. In general, however, magnetic perturbations will have a range of wavelengths, amplitudes and phases such that at different locations along a magnetic flux-tube regions of trapped electrons can develop and interact in a range of ways not accounted for in the previous analysis. We here explore how the process of trapping/detrapping itself leads to parallel energy mixing (
$v_{\parallel }$-diffusion), with the result of heating even for the case where the electron magnetic moments are conserved. The electron dynamics is here well accounted for by the drift kinetic framework pioneered by Kulsrud (Reference Kulsrud1983). In this framework the change of the electron energy is described by 
$\partial \mathcal {E} / \partial t= \mu \partial B / \partial t - e(\boldsymbol {v}_\|+ {\boldsymbol {v}}_D)\boldsymbol {\cdot }{\boldsymbol {E}}$, where 
${\boldsymbol {v}}_\|$ and 
${\boldsymbol {v}}_D$ are the field-aligned parallel streaming and guiding centre drift, respectively.
As a simplifying assumption and similar to Montag et al. (Reference Montag, Egedal, Lichko and Wetherton2017), Egedal et al. (Reference Egedal, Monkhorst, Lichko and Montag2018) and Lichko & Egedal (Reference Lichko and Egedal2020), in the present analysis we will only consider the electron dynamics in the fast transit time limit. In this limit it is assumed that the time scale associated with the electron bounce motion, 
$\tau _b$, is much shorter than the time scales characterizing the evolution of the magnetic perturbations, such that both the magnetic moment 
$\mu$, and the parallel action integral 
$J=\oint v_{\parallel }\,\textrm {d}l$ become adiabatic invariants. In addition, we assume a one-dimensional (1-D) spatial geometry where the electrons are confined in a single flux-tube. Orbits of electrons are then fully characterized by 
$\mu$ and 
$J$, and given the fast transit-time limit we can apply the multiple time scale method (Davidson Reference Davidson1972), where 
$f(\boldsymbol {x},\boldsymbol {v})$ is approximately constant along the ‘instantaneous’ bounce orbits. Consistent with Jeans theorem (Jeans Reference Jeans1915), it then follows that distributions can be expressed in the form 
$f=g(\mu ,J)$, where 
$g$ is an arbitrary function.
For the present analysis, however, we find it more useful to write 
$f(\mu ,\mathcal {E},t)=f_0(\mu ,\mathcal {E}_0)$, where 
$\mathcal {E}_0$ is the initial particle energy at a time 
$t_0$ of an initial known distribution, 
$f_0$. The problem of solving for the distribution 
$f(\mu ,\mathcal {E},t)$ is then reduced to obtaining a mapping between 
$\mathcal {E}(t)$ and 
$\mathcal {E}_0$ consistent with conservation of 
$\mu$ and 
$J$. Because we will only consider prescribed magnetic perturbations, there is no feedback of 
$f(\mu ,\mathcal {E},t)$ onto the wave dynamics. Determining the mapping 
$\mathcal {E}(t)\rightarrow \mathcal {E}_0$ then becomes a ‘single particle’ problem which can be solved by basically considering one point in phase space, 
$(\mu ,\mathcal {E},t)$, at a time. For general magnetic perturbations, determining the mapping 
$\mathcal {E}(t)\rightarrow \mathcal {E}_0$ is then a problem well suited for numerical orbit integration methods. Here, however, we will consider particularly simple magnetic geometries that allow explicit expressions for 
$\mathcal {E}_0(\mu ,\mathcal {E},t)$ to be determined, which (as we will see below) then in turn provide an explicit solution for the distribution function, 
$f(\mu ,\mathcal {E},t)=f_0(\mu ,\mathcal {E}_0(\mu ,\mathcal {E},t))$.
To illustrate how 
$v_{\parallel }$-diffusion can occur for adiabatic electrons with fixed magnetic moments, in figure 1 we consider a magnetic flux-tube with a square magnetic perturbation characterized by a reduced magnetic field 
$B_0$. Again, throughout the analysis we will assume that the electron transit time is fast compared with the time scale at which the magnetic field is changing. Thus, the evolution of the electron population will be adiabatic and reversible. As illustrated in figure 1(a), the magnetic well can trap electrons. The locations inside the magnetic well are parameterized by 
$x\in [0; 1]$, and at 
$x=d$ a narrow region is introduced where the magnetic field is increased to an enhanced value 
$B_T$. The width of this enhancement is assumed to be so narrow that we can neglect any heating 
$\mu \partial B / \partial t$ that result as it builds in time. Thus, the role of 
$B_T$ is solely to split electron orbits with total energy 
$\mathcal {E}< \mu B_T$ into locally trapped orbits in regions A and B, indicated in figure 1(b).
Figure 1. Sequence of magnetic perturbations considered for parallel velocity mixing, with the coloured arrows indicating distinct trapped orbit types. The deep magnetic square well of panel (a) is in panel (b) modified by a spatially narrow magnetic barrier at 
$x=d$ with 
$B=B_T$, separating regions A and B. In panel (c) the floor of region A is enhanced until 
$B=B_T$ is reached. In panel (d) the floor of region A (and the barrier) is reduced bringing the configuration back the initial state in panel (a).
From this point the magnetic geometry can be modified in a variety of ways. For example, in appendix A we analyse the result of changing dynamically the location 
$d$ of the barrier field 
$B_T$ and obtain very similar results to those to be derived now for a very different magnetic evolution. In this main section we consider a mixing cycle where we slowly raise the magnetic field in region A until it reaches the value of the barrier, 
$B_T$. During this process all the electrons trapped in region A will be energized at a rate 
$\mu \partial B / \partial t$ and become un-trapped as their total energies reach 
$\mathcal {E}=\mu B_T$. Here the electron orbits will undergo a transition from the blue orbit type to the red orbit type in figure 1(c). In region B the magnetic field is constant and no heating occurs, and compared with the trapped orbits in region A, the red orbit types are subject to reduced heating rates related the reduced fraction of time a given electron is present in region A. Then, as illustrated in figure 1(d) we again lower the magnetic field in region A and also eliminate the previous magnetic barrier at 
$x=d$. During this process, all the electrons initially confined to region B will observe orbit changes corresponding to the transition from the magenta to the red orbit types in figure 1(d). All electrons traversing regions A and B will be cooled proportionally the relative faction of the time they spend in region A.
As indicated above, the heating of the various orbit types can in principle be computed by integrating the orbit averaged value of 
$\mu \partial B / \partial t$. Meanwhile, the task of evaluating the energy changes is significantly simplified by considering the parallel action integral,
\begin{equation} J=\sqrt{\frac{m}{2}} \oint v_\|\,\textrm{d}l. \end{equation}
Here, the integral is taken over the trapped orbits’ bounce motion, and the unimportant factor 
$\sqrt {m/2}$ is included to ease the notation below. In addition, the use of 
$J$ makes the analysis more general as this framework also applies to less idealized configurations where the 
$- e(\boldsymbol {v}_\|+ \boldsymbol {v}_D)\cdot \boldsymbol {E}$-term (mentioned above) becomes important to the energization process (Montag et al. Reference Montag, Egedal, Lichko and Wetherton2017).
For orbits bouncing through both region A and region B we may differentiate between the contributions from the two regions,
\begin{equation} J=J_A + J_B , \end{equation}where
\begin{equation} J_A=\sqrt{\frac{m}{2}} \int_0^{d} v_\| \,\textrm{d}l ,\quad J_B=\sqrt{\frac{m}{2}} \int_{d}^1 v_\| \,\textrm{d}l. \end{equation} Introducing the present energy 
$\mathcal {E}$ and initial energy 
$\mathcal {E}_0$ of an electron in the configuration, using 
$v_\|=\sqrt {2/m}\,\sqrt {\mathcal {E}-\mu B}$, the present and initial values of these action contributions are trivially evaluated as
\begin{equation} J_A=d\sqrt{\mathcal{E}-\mu B},\quad J_{A0}=d\sqrt{\mathcal{E}_0-\mu B_0} \end{equation}and
\begin{equation} J_B=(1-d)\sqrt{\mathcal{E}-\mu B},\quad J_{B0}=(1-d)\sqrt{\mathcal{E}_0-\mu B_0}. \end{equation}
In general, the action integrals will be conserved while the magnetic configuration is evolving slowly in time. An exception to this occurs during the orbit transition in figure 1(c), where a new contribution, 
$J_{BT}$, from region B is acquired. Because the energy of a newly transitioned electron is 
$\mathcal {E}=\mu B_T$, in region B the parallel energy will be 
$\mu (B_T-B_0)$ and we find
\begin{equation} J_{BT}=(1-d)\sqrt{\mu (B_T-B_0)}. \end{equation}It then follows that electrons initially trapped in region A, will after their transition be characterized by
\begin{equation} J_A+J_B=J_{A0} + J_{BT}, \end{equation}from which we can relate the initial energy to the present energy,
\begin{equation} \mathcal{E}_0 = \frac{1}{d^2}\left[ (1-d) \left(\sqrt{\mathcal{E}- \mu B_0}-\sqrt{\mu(B_T-B_0)} \right) + d\sqrt{\mathcal{E}-\mu B} \right]^2 + \mu B_0. \end{equation}
While the electrons are confined in region A they experience the full heating provided by 
$\mu \partial B / \partial t$. This heating is stronger than the average cooling they observe when they transit both region A and region B, and 
$B$ is decreasing in region A. Consistently, from (2.8) it is readily shown that 
$\mathcal {E}_0<\mathcal {E}$ and it follows that all electrons originally in region A will gain energy during the mixing sequence.
We may consider the orbit transition in figure 1(d) where orbits confined to region B transition into orbits passing through both regions. This transition is different from that described above (where electrons cleared a barrier 
$\mu B_T$ and fell into a region of lower magnetic field 
$B_0 < B_T$, yielding a parallel energy boost). In the present transition there is no localized barrier, and the newly transitioned electrons will have 
$v_\|\simeq 0$ during their initial traversal of region A, and there are no new contributions to the action integral. Thus, for the electrons transitioning out of region B we have
\begin{equation} J_A + J_B = J_{B0}, \end{equation}such that
\begin{equation} \mathcal{E}_0 = \frac{ \left[d\sqrt{\mathcal{E}-\mu B} + (1-d) \sqrt{\mathcal{E}- \mu B_0}\right]^2}{(1-d)^2} + \mu B_0. \end{equation}
From (2.10) it can be shown that 
$\mathcal {E}_0>\mathcal {E}$ and all electrons which have undergone a transition out of region B will observe a net cooling. This is consistent with our expectation because these electrons only reach region A during the period where 
$\partial B / \partial t$ is negative.
With (2.8) and (2.10) we have obtained expressions for the initial energy as a function of the present energy for the orbits which have undergone orbit transitions. Similar expressions are also readily obtained for the orbits which have not undergone transitions simply by imposing 
$J_A=J_{A0}$, 
$J_B=J_{B0}$, and 
$J_A+ J_B=J_{A0} +J_{B0}$, for the ‘blue’, ‘magenta’ and ‘red’ orbit types, respectively. Thus, the application of the action integral permits a very effective evaluation of 
$\mathcal {E}_0$ as a function of 
$\mathcal {E}$ for all orbit classes continuous during the mixing sequence.
In figure 2 we illustrate the evolution of 
$\mathcal {E}_0(\mathcal {E})$ at selected times during the mixing sequence. In this figure the 
$y$-axes represent the present total kinetic energy 
$\mathcal {E}$ of electrons with magnetic moments 
$\mu$, while the colour contours describe their spectrum of initial energies 
$\mathcal {E}_0$. Figure 2(a) displays the initial range of relevant energies, where we simply have 
$\mathcal {E}=\mathcal {E}_0$. The black lines are the energy barriers due to the imposed magnetic field structure. Those electrons with present energy 
$\mathcal {E} >\mu B_T$ will be able to overcome the barrier separating region 
$A$ and region 
$B$. The changes in colour from one panel to the next then describe the evolution of the relationship between 
$\mathcal {E}$ and 
$\mathcal {E}_0$, as expressed in the derived equations. Because 
$\mu$ is conserved during the whole mixing process, and both 
$\mathcal {E}$ and 
$\mathcal {E}_0$ are proportional to 
$\mu$, the results of the figure become applicable to any value of 
$\mu$. At the time of figure 2(d) the magnetic field in region A has reached that of the barrier 
$B=B_T$, and all the electrons originally in region A now have energies larger than those of region B. In figure 2(e, f) the magnetic field of region A is reduced again and the magnetic barrier at 
$x=d$ is eliminated.
Figure 2. (a–g) Colour contour plots of the initial energy 
$\mathcal {E}_0$ as functions of position 
$x$ and present energy 
$\mathcal {E}$ as observed during the evolution of the magnetic well outlined in figure 1 with 
$d=0.4$ and 
$B_T/B_0=8$. Panel (h) illustrates the results of two complete mixing cycles.
In figure 2(g) the magnetic field has returned to its initial state. Consider an electron originally marginally trapped in region B with 
$\mathcal {E}_0=\mu B_T$, using (2.10) with 
$B=B_0$ we can solve for 
$\mathcal {E}$ to obtain the transition energy between the two electron populations after the mixing cycle is complete,
\begin{equation} \mathcal{E}_T= (1-d)^2 \mu(B_T-B_0) + \mu B_0. \end{equation}
Further, using (2.8) and (2.10) with 
$B=B_0$ we obtain the mapping between 
$\mathcal {E}_0$ and 
$\mathcal {E}$ after one complete mixing cycle,
\begin{equation} \mathcal{E}_0 = \begin{cases} \frac{\displaystyle \mathcal{E}-\mu B_0}{\displaystyle (1-d)^2} +\mu B_0, & \text{for}\ \mu B_0< \mathcal{E}< \mathcal{E}_T,\\ \frac{\displaystyle 1}{\displaystyle d^2}\left[ \sqrt{\mathcal{E}- \mu B_0} - (1-d) \sqrt{\mu(B_T-B_0)} \right]^2 + \mu B_0, & \text{for}\ \mathcal{E}_T<\mathcal{E}< \mu B_T,\\ \mathcal{E}, & \text{for}\ \mu B_T< \mathcal{E}. \end{cases} \end{equation} As is evident from (2.12) and figure 2 the energy gain 
$\Delta \mathcal {E}=\mathcal {E}-\mathcal {E}_0$ depends on the initial 
$\mathcal {E}_0$ as well as the initial location of the electrons. The electrons which gain the most energy are initially located in region A with vanishing parallel energy, such that 
$\mathcal {E}_0=\mu B_0$. After one mixing cycle these electrons will then have a total energy of 
$\mathcal {E}=\mathcal {E}_T$, marked in figure 2(g). On the other hand, the electrons that will be cooled the most are originally barely trapped in region B (i.e. 
$\mathcal {E}_0\sim \mu B_T$). After the mixing cycle, these will also have a present energy 
$\mathcal {E}=\mathcal {E}_T$. Meanwhile, region A electrons with 
$\mathcal {E}_0=\mu B_T$ as well as region B electrons with 
$\mathcal {E}_0=\mu B_0$ observe no change in their energies.
To characterize the effect of multiple mixing cycles we can evaluate (2.12) recursively. We introduce 
$\mathcal {E}_N$ as the electron energy after 
$N$ cycles and (2.12) then implies that
\begin{align} \mathcal{E}_{N-1} = \begin{cases} \displaystyle \frac{\mathcal{E}_N-\mu B_0}{(1-d)^2} +\mu B_0, & \text{for}\ \mu B_0< \mathcal{E}_N< \mathcal{E}_T, \\ \frac{\displaystyle 1}{\displaystyle d^2}\left[ \sqrt{\mathcal{E}_N- \mu B_0} - (1-d) \sqrt{\mu(B_T-B_0)} \right]^2 + \mu B_0, & \text{for}\ \mathcal{E}_T<\mathcal{E}_N< \mu B_T,\\ \mathcal{E}_N, & \text{for}\ \mu B_T< \mathcal{E}_N. \end{cases} \end{align}
With (2.13) we have now established a direct mapping between the energy 
$\mathcal {E}_N$ after 
$N$ mixing cycles and the initial energy 
$\mathcal {E}_0$. An example of 
$\mathcal {E}_0(\mathcal {E}_N)$ with 
$N=2$ is given in figure 2(h).
3. Parallel diffusion of 
$f_e$
As discussed in § 2, the electrons are governed by the drift kinetic equation, which, for the considered limit of slow magnetic field evolution and well magnetized electrons (such that 
$\textrm {d}\mu /\textrm {d}t=0$), simply takes the form 
$\textrm {d}f_e(\mathcal {E},\mu )/\textrm {d}t=0$ (Montag et al. Reference Montag, Egedal, Lichko and Wetherton2017). Assuming an initial electron distribution 
$f_{e0}(\mathcal {E},\mu )$, with (2.13) we then obtain the distribution that results after 
$N$ cycles as
\begin{equation} f_e(\mathcal{E}_N,\mu)= f_{e0}(\mathcal{E}_0(\mathcal{E}_N),\mu), \end{equation}
where 
$\mathcal {E}_0(\mathcal {E}_N)$ can be obtained from the recursion relation given in (2.13). As an example, starting with an initial Maxwellian 
$f_{e0}(\mathcal {E}_0,\mu )$ shown in figure 3(a), the results of one, two and five mixing cycles are illustrated in figure 3(b–d), respectively.
The changes in 
$f_e$ induced by the parallel mixing are fully reversible. However, we note how the number of stripes in the 
$f_e$ grows as 
$2^N$ such that at sufficiently large 
$N$ the smallest amount of scattering will be sufficient to smooth out the exponentially narrowing stripes. This will render 
$f_e$ independent of 
$\mathcal {E}_\|$, such that for the trapped ranges affected by the pumping we have 
$f_e=f_e(\mu )$. At this point the mixing process has run its course and no further changes will occur in 
$f_e$ by parallel mixing alone.
While the effect of parallel mixing, above, was calculated for a highly idealized magnetic geometry it is clear that the cause of the mixing of 
$f_e$ are the orbit transitions of the type introduced with figure 1(c). Therefore, any wave activity that leads to similar orbit transitions will cause equivalent mixing in naturally occurring systems.
4. Changes in $f_e$ due to combined ${\mathcal {E}_\parallel }$ and pitch angle mixing
In the following section we will derive a model for the heating that occurs when pitch angle scattering is included during the continuous mixing described above. We will formulate this model in terms of a slowly evolving 1-D velocity distribution 
$g(v,t)$. Any distribution as a function of speed can be written as an isotropic distribution in 
$(v_{\perp }, v_\|)$, and we denote an initial two-dimensional (2-D) distribution as 
$f(v_{\perp }, v_\|)\equiv \left \langle g \right \rangle _{\xi }$, an example of which is shown in figure 4(a) for the case where 
$g(v)$ is a simple Maxwellian. Furthermore, in our manipulations we will also use 
$\left \langle \cdots \right \rangle _{\xi }$ as an operator, which for any 2-D distribution yields a distribution fully scattered in the cosine-pitch-angle variable 
$\xi ={v_\parallel }/\sqrt {{v_\parallel }^2+{v_\perp }^2}$.
Figure 4. Illustration of how the 2-D distributions 
$\left \langle g \right \rangle _{\parallel }$ and 
$\left \langle \left \langle g \right \rangle _{\parallel } \right \rangle _{\xi }$ are determined from 
$\left \langle g \right \rangle _{\xi }$. In panels (a,b) the green lines are the trapped passing boundaries characterized by 
${\mathcal {E}_\parallel }=h{\mathcal {E}_\perp }$, where 
$h=(B_T/B_0-1)$. The 
${\mathcal {E}_\parallel }$-mixed distribution 
$\left \langle g \right \rangle _{\parallel }$ is determined from 
$\left \langle g \right \rangle _{\xi }$ by requiring particle conservation for the velocity phase-space elements of the type encircled in cyan. In turn, 
$\left \langle \left \langle g \right \rangle _{\parallel } \right \rangle _{\xi }$ in panel (c) is determined from 
$\left \langle g \right \rangle _{\parallel }$ by requiring particle conservation for the velocity phase-space elements of the type encircled in red in panels (b,c).
The distribution in figure 4(b) represents the result of the 
${v_\parallel }$-diffusion described above for electrons trapped by 
$B_T$. We denote this distribution as 
$\left \langle g \right \rangle _{\parallel }$ corresponding to a distribution completely mixed in the 
${v_\parallel }$-direction for the electrons within the trapped region. Here the trapped region is outlined by the green lines characterized by 
${v_\parallel }^2< h {v_\perp }^2$, where 
$h = (B_T/B_0-1)$ and 
$B_T$ is the value of the barrier introduced in figure 1(b). Mathematically, 
$\left \langle g \right \rangle _{\parallel }$ is obtained from 
$\left \langle g \right \rangle _{\xi }$ by particle conservation. In particular, we require that for any 
${v_\perp }$ the rectangular type areas in the trapped regions of differential width 
$d{v_\perp }$, as outlined by the areas encircled in cyan in figures 4(a) and 4(b), 
$\left \langle g \right \rangle _{\parallel }$ and 
$\left \langle g \right \rangle _{\xi }$ contain identical number of particles.
We next consider the scenario where 
$\left \langle g \right \rangle _{\parallel }$ is completely isotropized in pitch angle yielding the distribution here denoted 
$\left \langle \left \langle g \right \rangle _{\parallel } \right \rangle _{\xi }$. Mathematically, as outlined in figures 4(b) and 4(c) this distribution is also determined by imposing particle conservation, this time requiring that for any 
$v$ the differential speed elements 
$\textrm {d}v$, as outlined by the areas encircled in magenta in figures 4(b) and 4(c), contain identical number of particles in 
$\left \langle g \right \rangle _{\parallel }$ and 
$\left \langle \left \langle g \right \rangle _{\parallel } \right \rangle _{\xi }$. In appendix B we show that
\begin{equation} \left\langle \left\langle g \right\rangle_{{\parallel}} \right\rangle_{\xi}\simeq \left\langle g+ \delta g \right\rangle_{\xi}, \end{equation}where
\begin{equation} \delta g = \frac{h}{45 } \left(\frac{h}{1+h} \right)^{3/2} \frac{1}{v^2}\frac{\partial }{\partial v} v^4 \frac{\partial }{\partial v} g \end{equation}
and, repeated for convenience, 
$h=B_T/B_0-1$.
5. Evolution of the background distribution
Above, we introduced the 1-D distribution 
$g=g(v,t)$ for characterizing the isotropic component of the background plasma. The main goal of the present section is to derive an evolution equation that describes the slow evolution of 
$g$. To accomplish this we need to consider the full 2-D distribution, which we approximately describe as a linear combination of the fully 
${v_\parallel }$-mixed distribution 
$\left \langle g \right \rangle _{\parallel }$ and the fully pitch angle scattered distribution 
$\left \langle g \right \rangle _{\xi }$, such that
\begin{equation} f = (1-\alpha)\left\langle g \right\rangle_{\xi} + \alpha \left\langle g \right\rangle_{{\parallel}}. \end{equation}
The parameter 
$\alpha$ will be determined below and is dependent on the drive frequency, 
$\nu _{\parallel }$, of the parallel mixing compared with the characteristic frequency, 
$\nu _{\xi }$, of the pitch angle diffusion.
We further approximate the parallel mixing and pitch angle diffusion in terms of Krook-type operators, allowing us to write the kinetic equation as
\begin{equation} \frac{\partial f}{\partial t} = \nu_{{\parallel}}\left(\left\langle \,f \right\rangle_{{\parallel}} - f\right) + \nu_{\xi}\left(\left\langle \,f \right\rangle_{\xi} -f \right), \end{equation}
which we, through numerical analysis (not included), find is a reasonable approximation for 
$\nu _{\parallel } \gtrsim 3\nu _{\xi }$. Here 
$\nu _{\parallel }$ describes the characteristic frequency of the 
$v_{\parallel }$-diffusion process, which will be of the order of the frequencies describing the magnetic perturbations. Similarly, 
$\nu _{\xi }$ is the characteristic frequency of the pitch angle scattering process.
Inserting (5.1) into (5.2) yields
\begin{equation} \frac{\partial f}{\partial t} ={-} K \left(\left\langle g \right\rangle_{{\parallel}} - \left\langle g \right\rangle_{\xi} \right) + \nu_{\xi} \alpha\left\langle \delta g \right\rangle_{\xi}, \end{equation}with
\begin{equation} K= \nu_{\xi} \alpha -\nu_{{\parallel}} (1-\alpha), \end{equation}where we have used (4.1) together with the rules
\begin{equation} \left\langle \left\langle g \right\rangle_{\xi} \right\rangle_{\xi}=\left\langle g \right\rangle_{\xi},\quad \left\langle \left\langle g \right\rangle_{\xi} \right\rangle_{{\parallel}}= \left\langle g \right\rangle_{{\parallel}},\quad \left\langle \left\langle g \right\rangle_{{\parallel}} \right\rangle_{{\parallel}}=\left\langle g \right\rangle_{{\parallel}}. \end{equation}
Note that the first two of these rules follow because 
$g(v)$ is isotropic such that 
$\left \langle g \right \rangle _{\xi }=g$.
Next we use that direct differentiation of (5.1) with respect to time yields
\begin{equation} \frac{\partial f}{\partial t} = \dot{\alpha}\left(\left\langle g \right\rangle_{{\parallel}} -\left\langle g \right\rangle_{\xi} \right) + (1-\alpha)\left\langle \dot{g} \right\rangle_{\xi} + \alpha \left\langle \dot{g} \right\rangle_{{\parallel}}, \end{equation}
where we used the notation 
$\dot {g}=\partial g / \partial t$ and 
$\dot {\alpha }=\partial \alpha / \partial t$. Matching the terms in (5.3) and (5.6) proportional to 
$(\left \langle g \right \rangle _{\parallel } -\left \langle g \right \rangle _{\xi } )$ we find
\begin{equation} \dot{\alpha} ={-}K = \nu_{{\parallel}} (1-\alpha) - \nu_{\xi} \alpha. \end{equation}
This provides an evolution equation of the level of anisotropy parameterized by 
$\alpha$. At a time scale of the order of 
$1/\nu _{\parallel }$, the value of 
$\alpha$ will approach the steady-state solution described by 
$K=0$ for which
\begin{equation} \alpha = \frac{\displaystyle \nu_{{\parallel}}}{\displaystyle \nu_{{\parallel}}+\nu_{\xi}}. \end{equation}
Inserting (5.8) and 
$\dot {\alpha }=K=0$ into (5.3) and (5.6) and equating the resulting two expressions for 
$\partial f / \partial t$ we find
\begin{equation} \frac{\displaystyle \nu_{\xi} \nu_{{\parallel}}}{\displaystyle \nu_{{\parallel}}+\nu_{\xi}} \left\langle \delta g \right\rangle_{\xi} = \frac{\displaystyle \nu_{\xi}}{\displaystyle \nu_{{\parallel}}+\nu_{\xi}}\left\langle \dot{g} \right\rangle_{\xi} +\frac{\displaystyle \nu_{{\parallel}}}{\displaystyle \nu_{{\parallel}}+\nu_{\xi}} \left\langle \dot{g} \right\rangle_{{\parallel}}. \end{equation}
Then, by taking the 
$\left \langle \cdots \right \rangle _{\xi }$-average and using the approximation that 
$\left \langle \left \langle \dot {g} \right \rangle _{\parallel } \right \rangle _{\xi } \simeq \left \langle \dot {g} \right \rangle _{\xi }$ the right-hand side simplifies and we find
\begin{equation} \left\langle \dot{g} \right\rangle_{\xi} = \frac{\displaystyle \nu_{\xi}\nu_{{\parallel}}}{\displaystyle \nu_{{\parallel}}+\nu_{\xi}}\left\langle \delta g \right\rangle_{\xi}. \end{equation}
By inspection of (5.2) it becomes clear that the approximation 
$\left \langle \left \langle \dot {g} \right \rangle _{\parallel } \right \rangle _{\xi } \simeq \left \langle \dot {g} \right \rangle _{\xi }$, above, corresponds to the neglect of a second-order time-derivative term of the approximate size 
$(1/\nu _{\parallel })\partial \dot {g} /\partial t$.
Given (5.10), we may now apply the form in (4.2) to obtain the desired evolution equation for 
$g(v,t)$:
\begin{equation} \boxed{\frac{\partial g}{\partial t} = \frac{1}{v^2}\frac{\partial }{\partial v} v^2 D \frac{\partial }{\partial v} g\,,\quad D=\nu_{{\parallel}} v^2 {\mathcal{G}},} \end{equation}where
\begin{equation} {\mathcal{G}} = \frac{\displaystyle \nu_{\xi}}{\displaystyle \nu_{{\parallel}}+\nu_{\xi} } \frac{h}{45 } \left(\frac{h}{1+h} \right)^{3/2},\quad h=\frac{B_T}{B_0} -1. \end{equation}We have drawn a box around (5.11) as it represents the main result of our analysis.
6. Discussion and conclusion
The expression for 
$\partial g / \partial t$ in (5.11) has the form of velocity diffusion, where the diffusion coefficient 
$D\propto \nu _{\parallel } v^2$ describes a process with a diffusive step size proportional to velocity 
$\delta v\propto v$. Equivalently, the diffusive energy step size is proportional to energy, as is characteristic of a Fermi heating process. It is readily seen that a power-law distribution of the form 
$g\propto v^{-\gamma }$ with 
$\gamma =3$, represents a steady-state solution to (5.11). For a more realistic representation of a physical system, particle sources and sinks can be added to (5.11). In general, this will lead to power-law solutions with 
$\gamma > 3$ (Montag et al. Reference Montag, Egedal, Lichko and Wetherton2017). The diffusion equation in (5.11) (as well as the similar form obtained in Lichko & Egedal (Reference Lichko and Egedal2020)) is, therefore, consistent with the power law distributions recorded in situ by spacecraft throughout the solar wind and the Earth's magnetosphere.
For wave dynamics with a typical magnitude 
$\widetilde {\textrm {d}B} = \textrm {d}B/B_0$ we may approximate 
$B_T\simeq B_0+dB$ and it follows that 
$h\simeq \widetilde {\textrm {d}B}$. Given the dependency of (5.11) on 
$h$, the efficiency of the energy diffusion for small 
$\widetilde {\textrm {d}B}$ scales as 
$\widetilde {\textrm {d}B}^{5/2}$, but falls off to a linear scaling for larger order unity wave amplitudes. The present model is obtained using the Krook model in (5.2), which from preliminary numerical results (not included here) is found to be a good approximation when the system is characterized by weak pitch angle scattering, 
$\nu _{\xi }/\nu _{\parallel } \lesssim 1/3$. In figure 5 the blue lines illustrate the predictions of (5.12) for 
${\mathcal {G}}$, evaluated for the amplitudes of 
$B_T$ listed in the figure, and the full lines for 
$\nu _{\xi }/\nu _{\parallel } < 1/3$ correspond to the range where the model is expected to be accurate. For 
$\nu _{\xi }/\nu _{\parallel } \gtrsim 1/3$ the Krook model in (5.2) becomes inaccurate because the pitch angle scattering will cause the region A and region B electrons (see figure 1b) to mix without the separate 
$\mu \partial B / \partial t$ heating/cooling of the two regions. In fact, for 
$\nu _{\xi }/\nu _{\parallel } \gtrsim 1$ we expect that heating by magnetic pumping will be more efficient than heating by 
$v_{\parallel }$-mixing.
Figure 5. Blue lines: the energization rate 
${\mathcal {G}}$ by 
$v_{\parallel }$-mixing as a function of 
$\nu _{\xi }/\nu _{\parallel }$, calculated using (5.12) for 
$B_T/B_0 \in \{1.1, 1.2, 1.5, 2.3, 5 \}$. Indicated by full lines, the theory is expected to be valid for 
$\nu _{\xi }/\nu _{\parallel }<1/3$. Red lines: for comparison the efficiency of magnetic pumping the red lines represent the similar 
${\mathcal {G}}$ in (6) of Lichko & Egedal (Reference Lichko and Egedal2020), evaluated with 
$\nu /f_{\textrm {pump}}=\nu _{\xi }/\nu _{\parallel }$ and 
$C_K=1$, and considering the same magnetic perturbations as applied for the 
$v_{\parallel }$-mixing.
For comparison, the red lines in figure 5 are obtained from the model of magnetic pumping with trapped electrons developed in Lichko & Egedal (Reference Lichko and Egedal2020), where in (6) an expression is given for the form of 
${\mathcal {G}}_{\textrm {pump}}$ due to magnetic pumping, and we evaluate 
${\mathcal {G}}_{\textrm {pump}}$ for the same magnetic perturbations as yielded the blue lines in figure 5. Furthermore, in this comparison 
${\mathcal {G}}_{\textrm {pump}}$ is obtained assuming 
$\nu /f_{\textrm {pump}} = \nu _{\xi }/\nu _{\parallel }$. The model for 
${\mathcal {G}}_{\textrm {pump}}$ also includes a factor, 
$C_K$, that calibrates the efficiency of a Krook scattering model to the efficiency of the Lorentz scattering operator. The Krook scattering model implemented here in (5.2) is equivalent to 
$C_K=1$, and is thus the value used in calculating the red lines.
We observe that the predicted heating from 
$v_{\parallel }$-mixing is up to two orders of magnitude larger than that expected from magnetic pumping. Physically, this result is reasonable because net energization in the magnetic pumping model requires pitch angle scattering during each pumping cycle. In contrast, the 
$v_{\parallel }$-mixing yields finite 
${\mathcal {E}_\parallel }$-energization even if 
$\nu _{\xi }=0$ (corresponding to the changes in the distributions between figures 4a and 4b). As in Landau damping, for the limit of 
$\nu _{\xi }=0$ the process is fully reversible for the hypothetical case where the mixing cycle is exactly reversed. But given the fine scale structures that develop in velocity space after just a few mixing cycles, such a reversal is unlikely to occur in any physical system. As emphasized in Lichko & Egedal (Reference Lichko and Egedal2020), the electron energization is caused by mechanical work through the term 
$p_{\perp } \boldsymbol {\nabla } \boldsymbol {\cdot } \boldsymbol {v}_{\perp }$ and is linked to the development of pressure anisotropy, which in the pumping model is continuously being isotropized by pitch angle scattering. Meanwhile, for the 
$v_{\parallel }$-mixing this anisotropy can build during multiple mixing cycles, and becomes more pronounced than the anisotropy that develop during a single magnetic pump cycle.
The regime with 
$\nu _{\xi }/\nu _{\parallel } \ll 1/3$ is likely to be relevant to the solar wind for which a recent analysis of the Strahl electrons show that pitch angle scattering is mostly limited to the low level provided by Coulomb collisions between electrons and ions (Horaites, Boldyrev & Medvedev Reference Horaites, Boldyrev and Medvedev2019). Meanwhile, for the MMS bow-shock encounter analysed in Lichko & Egedal (Reference Lichko and Egedal2020) we estimate that 
$\nu _{\xi }/\nu _{\parallel } \simeq 1/2$, whereas the analysis of a similar MMS bow-shock event (Amano et al. Reference Amano, Katou, Kitamura, Oka, Matsumoto, Hoshino, Saito, Yokota, Giles and Paterson2020) infer much larger values of 
$\nu _{\xi }/\nu _{\parallel }$. In future studies of in situ spacecraft data, to help determine the relevant value of 
$\nu _{\xi }/\nu _{\parallel }$ of a given dataset, we note that (5.1) and (5.8) can be fitted to electron data as provided by, for example, MMS (Burch et al. Reference Burch, Moore, Torbert and Giles2016) and may prove useful for inferring 
$\nu _{\xi }/\nu _{\parallel }$ directly from the observations.
The magnetic configurations considered here are highly idealized. This adds to the need for developing new analytical and numerical techniques for simultaneously evaluating heating by both 
$v_{\parallel }$-mixing and magnetic pumping for more general magnetic perturbation geometries. Nevertheless, while the configurations considered are useful for providing physical insight into the heating mechanism, we expect that the energization theoretical rates obtained will prove representative also for naturally occurring systems. This is emphasized by the result that the very different scenarios considered in the main text and appendix A, respectively, provide similar levels of 
$v_{\parallel }$-mixing.
Editor William Dorland thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.
Appendix A
In this appendix we consider a modified 
$v_{\parallel }$-mixing scenario, which turns out to yield results very similar to those of §§ 2 and 3. As outlined in figure 6(a) we again consider a magnetic barrier at 
$x=d$ with height 
$\mu B_T$, separating the spatial dimension into region A and region B. We then examine the 
$v_{\parallel }$-mixing that occurs as region A is expanded at the expense of region B, corresponding to the location of the barrier being moved from 
$d'=d$ towards 
$d'=1$. Requiring again that the parallel action integrals be conserved 
$(J_A=J_{A0})$, it follows that the region A electrons are being cooled with
\begin{equation} \mathcal{E}_0=\left(\frac{\displaystyle d'}{\displaystyle d}\right)^2\left(\mathcal{E}-\mu B_0\right) + \mu B_0. \end{equation}
Meanwhile, the region B electrons are being heated and the initial energy 
$\mathcal {E}_0$ and present energy 
$\mathcal {E}$ are similarly described by
\begin{equation} \mathcal{E}_0=\left(\frac{\displaystyle 1-d'}{\displaystyle 1-d}\right)^2\left(\mathcal{E}-\mu B_0\right) + \mu B_0. \end{equation}
Figure 6. Illustration of 
$v_{\parallel }$-mixing by changing the location of a magnetic barrier initially located at 
$x=d$. In panels (a–d) the colour contours represent 
$\mathcal {E}_0$ as a function of 
$x$ and 
$\mathcal {E}$, with the initial profile in panel (a), while panels (b,c) are computed with the barrier moved to 
$d'=0.6$ and 
$d'=1$, respectively. Panel (d) corresponds to the result of two complete mixing cycles. (e–g) Electron distributions computed using (A 7) for one, two and five complete mixing cycles, respectively.
As region B is contracting the electrons confined to this region are all subject to 
$v_{\parallel }$ heating and will eventually reach the energy 
$\mathcal {E}=\mu B_T$ where they can overcome the barrier. After clearing the barrier they will immediately experience the cooling of region A and will, therefore, become trapped in region A. For an initial value of 
$\mathcal {E}_0$ we obtain from (A 2) the value of 
$d'=d_T$ when this transition occurs,
\begin{equation} \left(1-d_T\right)^2= (1-d)^2 \left(\frac{\displaystyle \mathcal{E}_0-\mu B_0}{\displaystyle \mu(B_T-B_0)}\right). \end{equation} To further established the relationship between 
$\mathcal {E}_0$ and 
$\mathcal {E}$ after the transition, we characterize the subsequent cooling in region A for 
$d_T\leq d'\leq 1$. Considering (A 1), it follows that this cooling must be governed by
\begin{equation} \mu B_T=\left(\frac{\displaystyle d'}{\displaystyle d_T}\right)^2\left(\mathcal{E}-\mu B_0\right) + \mu B_0. \end{equation}
Combining (A 3) and (A 4) by eliminating 
$d_T$ while solving for 
$\mathcal {E}_0$ we obtain
\begin{equation} \mathcal{E}_0=\frac{\displaystyle \mu(B_T-B_0)}{\displaystyle (1-d)^2}\left(1-d'\sqrt{\frac{\displaystyle \mathcal{E}-\mu B_0}{\displaystyle \mu(B_T-B_0)}}\,\right)^2+\mu B_0. \end{equation}We further introduce the transition energy
\begin{equation} \mathcal{E}_T= \frac{\displaystyle d^2}{\displaystyle {d'}^2} \,\mu(B_T-B_0) + \mu B_0, \end{equation}
obtained by solving (A 1) for 
$\mathcal {E}$ with 
$\mathcal {E}_0=\mu B_T$. The electrons in region A are then characterized by (A 1) for 
$\mu B_0 \leq \mathcal {E} \leq \mathcal {E}_T$, and by (A 5) for 
$\mathcal {E}_T \leq \mathcal {E} \leq \mu B_T$. The electrons in region B are characterized by (A 2) for the full interval 
$\mu B_0 \leq \mathcal {E} \leq \mu B_T$. With the initial barrier at 
$d=0.4$, the derived relationship between 
$\mathcal {E}$ and 
$\mathcal {E}_0$ is illustrated in figure 6(b,c) evaluated for 
$d'=0.6$ and 
$d'=1$, respectively. Note that electrons with 
$\mathcal {E} > \mu B_T$ are not affected by the changes in the location of the magnetic barrier.
In the present scenario, a mixing cycle is complete when 
$d'=1$ and all electrons are then characterized by the region A expressions. Similar to the derivation in § 2, we readily obtain recurrence relations for the impact of 
$N$ complete mixing cycles,
\begin{equation} \mathcal{E}_{N-1} = \begin{cases} \frac{\displaystyle \mathcal{E}_N-\mu B_0}{\displaystyle d^2} +\mu B_0, & \text{for}\ \mu B_0< \mathcal{E}_N < \mathcal{E}_T,\\ \frac{\displaystyle \mu(B_T- B_0)}{\displaystyle (1-d)^2}\left(1-\sqrt{\frac{\displaystyle \mathcal{E}_N-\mu B_0}{\displaystyle \mu(B_T-B_0)}}\right)^2 + \mu B_0, & \text{for}\ \mathcal{E}_T<\mathcal{E}< \mu B_T\\ \mathcal{E}_N, & \text{for}\ \mu B_T< \mathcal{E}_N, \end{cases} \end{equation}
and because 
$d'=1$ the transition energy is here characterized by
\begin{equation} \mathcal{E}_T= d^2\mu(B_T-B_0) + \mu B_0. \end{equation}
In figure 6(d) we display the predictions of (A 7) computed for two mixing cycles, and similar to the distributions in § 3, figure 6(e–g) display the distributions that result after one, two and five cycles. Although the mixing process here is different from that of §§ 2 and 3, the final result is again a rapid 
$v_{\parallel }$ mixing and diffusion for the magnetically trapped electrons.
Appendix B
We will here derive the expression for 
$\delta g$ given in (4.2). For this we apply the procedure outlined in figure 4 imposing particle conservation between 
$\left \langle g \right \rangle _{\xi }$, 
$\left \langle g \right \rangle _{\parallel }$ and 
$\left \langle \left \langle g \right \rangle _{\parallel } \right \rangle _{\xi }$ for the differential velocity region encircled by the cyan and magenta lines, respectively. In our analysis we will consider the distributions of the form 
$f({\mathcal {E}_\parallel },{\mathcal {E}_\perp })$ normalized such that 
$n=\int f({\mathcal {E}_\parallel },{\mathcal {E}_\perp }) d^3v$. Because
\begin{equation} \textrm{d}v_{{\parallel}} = \frac{\displaystyle \textrm{d}{\mathcal{E}_\parallel}}{\displaystyle mv_{{\parallel}}}=\frac{\displaystyle \textrm{d}{\mathcal{E}_\parallel}}{\displaystyle \sqrt{2m{\mathcal{E}_\parallel}}},\quad 2{\rm \pi}{v_\perp}\,\textrm{d}{v_\perp} = \frac{\displaystyle 2{\rm \pi}}{\displaystyle m} \,\textrm{d}{\mathcal{E}_\perp} \end{equation}we have
\begin{equation} n= \frac{\displaystyle {\rm \pi}\sqrt{2}}{\displaystyle m^{3/2}}\iint f({\mathcal{E}_\parallel},{\mathcal{E}_\perp}) \frac{\displaystyle 1}{\displaystyle {\mathcal{E}_\parallel}^{1/2}}\, \textrm{d}{\mathcal{E}_\parallel} d{\mathcal{E}_\perp}. \end{equation} First, the background distribution 
$\left \langle g \right \rangle _{\xi }$ is isotropic, but during the mixing process rapid diffusion occurs in 
${\mathcal {E}_\parallel }$ for all the electrons trapped by 
$B_T$. Again, the trapped electrons are those with 
${\mathcal {E}_\parallel }< h {\mathcal {E}_\perp }$, where 
$h = B_T/B_0-1$, and within this fully diffused velocity region of 
$\left \langle g \right \rangle _{\parallel }$ is independent of 
${\mathcal {E}_\parallel }$; we will characterize this part of the distribution as 
${f_\perp }({\mathcal {E}_\perp })$, i.e. 
${f_\perp }({\mathcal {E}_\perp })= \left \langle g \right \rangle _{\parallel }$ for 
${\mathcal {E}_\parallel }< h {\mathcal {E}_\perp }$. From (B 2), particle conservation for the differential velocity regions outlined in cyan in figure 4(a,b) then imposes that
\begin{equation} \Delta{\mathcal{E}_\perp} \int_0^{h{\mathcal{E}_\perp}}{f_\perp}({\mathcal{E}_\perp}) \frac{\displaystyle 1}{\displaystyle {\mathcal{E}_\parallel}^{1/2}}\, \textrm{d}{\mathcal{E}_\parallel} =\Delta{\mathcal{E}_\perp} \int_0^{h{\mathcal{E}_\perp}} g(\mathcal{E}) \frac{\displaystyle 1}{\displaystyle {\mathcal{E}_\parallel}^{1/2}}\, \textrm{d}{\mathcal{E}_\parallel} \end{equation}or
\begin{equation} {f_\perp}({\mathcal{E}_\perp}) = \frac{\displaystyle 1}{\displaystyle 2(h{\mathcal{E}_\perp})^{1/2}} \int_0^{h{\mathcal{E}_\perp}} g(\mathcal{E}) \frac{\displaystyle 1}{\displaystyle {\mathcal{E}_\parallel}^{1/2}}\, \textrm{d}{\mathcal{E}_\parallel}. \end{equation}
For approximate evaluation of this integral we use that 
$\mathcal {E}={\mathcal {E}_\parallel }+{\mathcal {E}_\perp }$ and Taylor expand 
$g$ about 
${\mathcal {E}_\perp }$, such that
\begin{equation} g(\mathcal{E}) \simeq g({\mathcal{E}_\perp}) + g^\prime({\mathcal{E}_\perp}){\mathcal{E}_\parallel} + \frac{1}{2} g^{\prime\prime}({\mathcal{E}_\perp}){\mathcal{E}_\parallel}^2, \end{equation}and it then follows that
\begin{align} {f_\perp}({\mathcal{E}_\perp}) &\simeq \frac{\displaystyle 1}{\displaystyle 2(h{\mathcal{E}_\perp})^{1/2}}\left[ 2g {\mathcal{E}_\parallel}^{1/2} +\frac{2}{3} g^{\prime} {\mathcal{E}_\parallel}^{3/2}+ \frac{1}{5} g^{\prime\prime} {\mathcal{E}_\parallel}^{5/2} \right]_0^{h{\mathcal{E}_\perp}},\nonumber\\ &\simeq g({\mathcal{E}_\perp}) +\frac{1}{3}h{\mathcal{E}_\perp} g^{\prime} ({\mathcal{E}_\perp}) +\frac{1}{10}(h{\mathcal{E}_\perp})^2 g^{\prime\prime} ({\mathcal{E}_\perp}). \end{align} For what comes next, Taylor expansion of 
${f_\perp }({\mathcal {E}_\perp })$ to second order becomes useful:
\begin{equation} {f_\perp}({\mathcal{E}_\perp}) \simeq {f_\perp}(\mathcal{E}) - {f_\perp}^\prime(\mathcal{E}) {\mathcal{E}_\parallel} + \frac{1}{2} {f_\perp}^{\prime\prime}(\mathcal{E}){\mathcal{E}_\parallel}^2 . \end{equation}
We then use (B 6) to obtain expressions for the derivatives of 
${f_\perp }$ such that
\begin{equation} {f_\perp}^\prime(\mathcal{E}) \simeq \left(1+\frac{h}{3} \right) g^{\prime}(\mathcal{E}) + \frac{h}{3}\mathcal{E} g^{\prime\prime}(\mathcal{E})) +\frac{1}{5}h^2\mathcal{E} g^{\prime\prime} (\mathcal{E}) \end{equation}and
\begin{equation} {f_\perp}^{\prime\prime}(\mathcal{E}) \simeq \left(1+\frac{2h}{3} +\frac{h^2}{5} \right) g^{\prime\prime}(\mathcal{E}). \end{equation}
Using the cosine-pitch-angle variable introduced above we have 
${\mathcal {E}_\parallel }=\xi ^2\mathcal {E}$, and it follows that:
\begin{align} {f_\perp}({\mathcal{E}_\perp})&\simeq g(\mathcal{E}) +\frac{1}{3}h\mathcal{E} g^{\prime} (\mathcal{E}) +\frac{1}{10}(h\mathcal{E})^2 g^{\prime\prime} (\mathcal{E}) \nonumber\\ &\quad -\xi^2\mathcal{E} \left( \left(1+\frac{h}{3} \right) g^{\prime}(\mathcal{E}) + \left( \frac{h}{3} +\frac{h^2}{5}\right)\mathcal{E} g^{\prime\prime} (\mathcal{E})\right) \nonumber\\ &\quad + \frac{\xi^4}{2}\mathcal{E}^2 \left(1+\frac{2h}{3} +\frac{h^2}{5} \right) g^{\prime\prime}(\mathcal{E}). \end{align} With (B 10) we now have an expression for the diffused region of 
$\left \langle g \right \rangle _{\parallel }$ in terms of 
$g$, readily evaluated as a function of 
$\mathcal {E}$ and 
$\xi$. To continue and obtain an expression for 
$\delta g= \left \langle \left \langle g \right \rangle _{\parallel }-\left \langle g \right \rangle _{\xi } \right \rangle _{\xi }$ we apply that the number of particles in the differential speed intervals encircled in magenta in figure 4(b,c) must be identical. In general, the number of particles in an interval 
$dv$ can be computed as 
$4{\rm \pi} v^2\,\textrm {d}v\int _0^1 f(v,\xi )\,\textrm {d}\xi$. Meanwhile, 
$\left \langle g \right \rangle _{\parallel }$ and 
$\left \langle g \right \rangle _{\xi }$ only differ in the trapped region characterized by 
$\xi \leq k$, where 
$k^2=h/(1+h)$. It then follows that:
\begin{equation} \delta g \int_0^{1}\,\textrm{d}\xi = \int_0^{k} (\,{f_\perp}({\mathcal{E}_\perp}) -g(\mathcal{E}) )\,\textrm{d}\xi. \end{equation}
Here, of course, 
$\int _0^1\,\textrm {d}\xi =1$, and we proceed to evaluate directly the right-hand side using (B 10), well suited for the required integration over 
$\xi$ at constant 
$\mathcal {E}$:
\begin{align} \delta g&\simeq \frac{1}{3}kh\mathcal{E} g^{\prime} (\mathcal{E}) +\frac{1}{10}k(h\mathcal{E})^2 g^{\prime\prime} (\mathcal{E}) \nonumber\\ &\quad - \frac{1}{3} k^3\mathcal{E} \left( \left(1+\frac{h}{3} \right) g^{\prime}(\mathcal{E}) + \left(\frac{h}{3} +\frac{h^2}{5}\right)\mathcal{E} g^{\prime\prime} (\mathcal{E})\right) \nonumber\\ &\quad + \frac{1}{10}k^5\mathcal{E}^2\left( \left(1+\frac{2h}{3} +\frac{h^2}{5} \right) g^{\prime\prime}(\mathcal{E})\right). \end{align}This expression has the form
\begin{equation} \delta g\simeq A \mathcal{E} g^{\prime} (\mathcal{E}) + B\mathcal{E}^2 g^{\prime\prime} (\mathcal{E}), \end{equation}with
\begin{equation} \frac{A}{k}=\frac{1}{3}h -\frac{1}{3} k^2 \left(1+\frac{h}{3} \right) \end{equation}and
\begin{equation} \frac{B}{k}= \frac{1}{10}h^2 -\frac{1}{9} k^2h -\frac{1}{15} k^2h^2+\frac{1}{10}k^4 \left(1+\frac{2h}{3} +\frac{h^2}{5} \right). \end{equation}
Using 
$k^2=h/(1+h)$, the expressions for 
$A$ and 
$B$ reduce to
\begin{equation} A=\frac{2}{9} h\left(\frac{h}{1+h}\right)^{3/2}, \quad B=\frac{2}{5} A + \frac{4}{75} h^2 \left(\frac{h}{1+h}\right)^{5/2}. \end{equation}We further notice that (B 13) can also be written as
\begin{equation} \delta g\simeq A \frac{v}{2} \frac{\partial g}{\partial v} + B\left(\frac{-v}{4} \frac{\partial g}{\partial v} + \frac{v^2}{4} \frac{\partial ^2g}{\partial v^2}\right). \end{equation}
To within the order and accuracy of the applied Taylor expansions we have 
$B=2A/5$, and the result stated in (4.2), follows from simple manipulations
\begin{equation} \delta g \simeq \frac{A}{10} \frac{1}{v^2}\frac{\partial }{\partial v} v^4 \frac{\partial }{\partial v} g . \end{equation}
