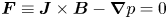2. The DESC code

DESC is a recently developed (Dudt & Kolemen Reference Dudt and Kolemen2020) pseudospectral code for computing 3-D MHD equilibria. DESC computes 3-D MHD equilibria by solving the force balance equations $\boldsymbol {J} \times \boldsymbol {B} - \boldsymbol {\nabla } p = 0$ as opposed to the more common variational method which minimizes the MHD energy $\int _V (B^2/2\mu _0 + p) \,{\rm d}V$. The independent variables in the equation are the positions of the flux surfaces $(R,Z)$ as well as the stream function $\lambda$, defined as the difference between the boundary poloidal angle $\theta$ and the straight-field-line poloidal angle $\vartheta = \theta + \lambda$. These quantities are discretized in a Fourier–Zernike basis, using a Fourier series in the toroidal direction and Zernike polynomials in the poloidal/radial directions. After discretization, the equilibrium equation is expressed as a set of nonlinear algebraic equations $\boldsymbol {f}(\boldsymbol {x}, \boldsymbol {c}) = 0$, where $\boldsymbol {x}$ is a vector containing the spectral coefficients of $R$, $Z$ and $\lambda$, while $\boldsymbol {c}$ contains fixed parameters that define the equilibrium problem, such as the pressure and rotational transform profiles and the fixed boundary shape.

Since its original publication (Dudt & Kolemen Reference Dudt and Kolemen2020), DESC has undergone a major upgrade that involved porting it from MATLAB to Python in order to take advantage of the JAX library (Bradbury et al. Reference Bradbury, Frostig, Hawkins, Johnson, Leary, Maclaurin, Necula, Paszke, VanderPlas and Wanderman-Milne2018) for automatic differentiation and just-in-time compilation. Initially developed for machine learning applications, JAX provides a NumPy-like (Van Der Walt, Colbert & Varoquaux Reference Van Der Walt, Colbert and Varoquaux2011; Harris et al. Reference Harris, Millman, van der Walt, Gommers, Virtanen, Cournapeau, Wieser, Taylor, Berg and Smith2020) application programming interface for common mathematical operations and allows arbitrary functions to be differentiated using forward- or reverse-mode automatic differentiation. This allows the calculation of exact derivatives of the objective function automatically, rather than having to code them by hand which is time-consuming and error prone, or using finite differences which are computationally expensive and can be inaccurate. It is also much more flexible as new objective functions can be added and optimized by defining only the forward pass, which is of great use in stellarator optimization where new objectives may be added in the future. JAX also allows for just-in-time compiling of code to both central and graphics processing units which significantly speeds up calculation, approaching speeds of traditional compiled languages, avoiding one of the primary limitations of Python for scientific computing. Additionally, given that the vast majority of new supercomputers heavily leverage graphics processing units, and this trend is likely to continue, using JAX allows DESC to take full advantage of all the compute capability available, rather than being limited to central-processing-unit-only parallelization like many legacy codes. This allows a ‘best of both worlds’ approach where the code is easy to use, maintain, adapt and upgrade, while still being fast enough for production applications.

Several aspects also make DESC the ideal code for implementing the perturbation method outlined in § 3:

1. (i) Using a pseudospectral discretization significantly reduces the number of independent variables, resulting in smaller Jacobian matrices.

2. (ii) Using JAX allows fast and accurate computation of the required derivatives and Jacobian–vector products.

3. (iii) Formulating the problem as a system of nonlinear equations and solving them in a least-squares sense also effectively gives an extra order of derivative for free.

This last point can be seen by considering the least-squares problem

(2.1)\begin{equation} \min_{\boldsymbol{x}} y(\boldsymbol{x}) \equiv \frac{1}{2} \boldsymbol{f}(\boldsymbol{x})^{\rm T} \boldsymbol{f}(\boldsymbol{x}), \end{equation}

where $\boldsymbol {f}$ is a vector valued function and $y$ is the sum of squares of the residuals of $\boldsymbol {f}$. The gradient of $y$ is given by

(2.2)\begin{equation} \frac{{\rm d} y}{{\rm d} \boldsymbol{x}} = \boldsymbol{f}^{\rm T} \frac{{\rm d} \boldsymbol{f}}{{\rm d} \boldsymbol{x}}, \end{equation}

and its Hessian (matrix of second partial derivatives) is given by

(2.3)\begin{equation} \frac{{\rm d}^2y}{{\rm d} \boldsymbol{x}^2} = \frac{{\rm d} \boldsymbol{f}}{{\rm d} \boldsymbol{x}}^{\rm T} \frac{{\rm d} \boldsymbol{f}}{{\rm d} \boldsymbol{x}} + \boldsymbol{f}^{\rm T} \frac{{\rm d}^2 \boldsymbol{f}}{{\rm d} \boldsymbol{x}^2}. \end{equation}

Given that $\boldsymbol {f}$ is the function we are trying to minimize in the least-squares sense, we can generally assume that the second term in the Hessian is negligible compared with the first, the so-called ‘small residual approximation’ (Nocedal & Wright Reference Nocedal and Wright2006). This gives an approximate Hessian ${{\rm d}^2 y}/{{\rm d} \boldsymbol {x}^2} \sim ({{\rm d} \boldsymbol {f}}/{{\rm d} \boldsymbol {x}}^{\rm T}) ({{\rm d} \boldsymbol {f}}/{{\rm d} \boldsymbol {x}})$, meaning that using only first-derivative information about $\boldsymbol {f}$ gives us both first- and second-derivative information about $y$. In addition, the approximate Hessian that this gives is always positive semi-definite, leading to a convex subproblem which is easy to solve.

3. Perturbations

A general fixed-boundary equilibrium problem can be described by a set of parameters $\boldsymbol {c} = \{R_b, Z_b, p, \iota, \varPsi \}$, where $R_b, Z_b$ are the $R,Z$ coordinates of the boundary surface, $p$ is the pressure profile, $\iota$ is the rotational transform and $\varPsi$ is the total toroidal flux through the torus. In many spectral equilibrium codes (Hirshman & Whitson Reference Hirshman and Whitson1983a; Dudt & Kolemen Reference Dudt and Kolemen2020), the independent variables that define the equilibrium can be given by $\boldsymbol {x} = [R_{lmn},Z_{lmn},\lambda _{lmn}]$, where $R_{lmn}$, $Z_{lmn}$ and $\lambda _{lmn}$ are spectral coefficients of the flux surface positions and the poloidal stream function (indexed by $l$ in the radial direction, $m$ in the poloidal direction and $n$ in the toroidal direction). The condition of MHD equilibrium can then be written as a (possibly vector-valued) nonlinear algebraic equation involving the fixed parameters and independent variables, $\boldsymbol {f}(\boldsymbol {x},\boldsymbol {c})=0$. The function $f$ is the discretized form of the general MHD force balance $\boldsymbol {J} \times \boldsymbol {B} - \boldsymbol {\nabla } p = 0$ (Dudt & Kolemen Reference Dudt and Kolemen2020), or a condition on the gradient of the energy functional $W = \int _V (B^2/2\mu _0 + p) \,{\rm d}V$ (Hirshman & Whitson Reference Hirshman and Whitson1983a).

Given a set of parameters $\boldsymbol {c}$ and a solution vector $\boldsymbol {x}$ which satisfy $\boldsymbol {f}(\boldsymbol {x},\boldsymbol {c}) = 0$, we wish to find how the equilibrium would change if the parameters $\boldsymbol {c}$ are perturbed to $\boldsymbol {c} + \Delta \boldsymbol {c}$. For instance, we may have a solution for a vacuum equilibrium and want to see how adding finite pressure changes it, or we may start with a 2-D tokamak solution and add a 3-D perturbation to the boundary shape to form a stellarator.

We assume that the new equilibrium is given by $\boldsymbol {x} + \Delta \boldsymbol {x}$, and expand $f$ in a Taylor seriesFootnote ¹ :

(3.1)\begin{gather} \boldsymbol{f}(\boldsymbol{x}+\Delta \boldsymbol{x},\boldsymbol{c}+ \Delta \boldsymbol{c}) = \boldsymbol{f}(\boldsymbol{x},\boldsymbol{c}) + \frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}}\Delta \boldsymbol{x} + \frac{\partial \boldsymbol{f}}{\partial \boldsymbol{c}}\Delta \boldsymbol{c} + \frac{1}{2}\frac{\partial^2 \boldsymbol{f}}{\partial \boldsymbol{x}^2}\Delta \boldsymbol{x}\Delta \boldsymbol{x}\nonumber\\ +\, \frac{1}{2} \frac{\partial^2 \boldsymbol{f}}{\partial \boldsymbol{c}^2}\Delta \boldsymbol{c}\Delta \boldsymbol{c} + \frac{\partial^2 \boldsymbol{f}}{\partial \boldsymbol{x}\partial \boldsymbol{c}}\Delta \boldsymbol{x}\Delta \boldsymbol{c} + O(\Delta x^3) . \end{gather}

We wish to solve this equation for $\Delta \boldsymbol {x}$ such that $\boldsymbol {f}(\boldsymbol {x}+\Delta \boldsymbol {x},\boldsymbol {c}+ \Delta \boldsymbol {c}) = 0$. At first order this is a straightforward algebraic equation, but at higher orders it becomes a tensor polynomial equation which can be difficult or impossible to solve efficiently (for example, if $\boldsymbol {f}$ is a vector-valued function, just storing the second-derivative tensor in memory could require upwards of 100 GB). Instead of seeking a direct solution, we can try a perturbative approach, were we introduce an arbitrary small parameter $\epsilon$ and further expand $\Delta \boldsymbol {x}$ and $\Delta \boldsymbol {c}$ in a perturbation series in powers of $\epsilon$ (we assume that $\Delta \boldsymbol {c}$ is known a priori and so only a first-order term is required):

(3.2)\begin{gather} \Delta \boldsymbol{x} = \epsilon \boldsymbol{x}_1 + \epsilon^2 \boldsymbol{x}_2 + \cdots , \end{gather}

(3.3)\begin{gather}\Delta \boldsymbol{c} = \epsilon \boldsymbol{c}_1. \end{gather}

Plugging this into (3.1) (and setting $\boldsymbol {f}(\boldsymbol {x},\boldsymbol {c}) = \boldsymbol {f}(\boldsymbol {x}+\Delta \boldsymbol {x}, \boldsymbol {c} + \Delta \boldsymbol {c})=0$) we get

(3.4)\begin{gather} 0 = \frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}}(\epsilon \boldsymbol{x}_1 + \epsilon^2 \boldsymbol{x}_2) + \frac{\partial \boldsymbol{f}}{\partial \boldsymbol{c}}\epsilon \boldsymbol{c}_1 + \frac{1}{2} \frac{\partial^2 \boldsymbol{f}}{\partial \boldsymbol{x}^2}(\epsilon \boldsymbol{x}_1 + \epsilon^2 \boldsymbol{x}_2)(\epsilon \boldsymbol{x}_1 + \epsilon^2 \boldsymbol{x}_2) \nonumber\\ + \frac{1}{2} \frac{\partial^2 \boldsymbol{f}}{\partial \boldsymbol{c}^2}\epsilon \boldsymbol{c}_1 \epsilon \boldsymbol{c}_1 + \frac{\partial^2 \boldsymbol{f}}{\partial \boldsymbol{x}\partial \boldsymbol{c}}(\epsilon \boldsymbol{x}_1 + \epsilon^2 \boldsymbol{x}_2) \epsilon \boldsymbol{c}_1 + O(\Delta x^3) . \end{gather}

We can then collect powers of $\epsilon$ and set each order of $\epsilon$ to zero in turn. The first-order equation gives

(3.5)\begin{gather} {0} =\frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}}\epsilon \boldsymbol{x}_1 + \frac{\partial \boldsymbol{f}}{\partial \boldsymbol{c}}\epsilon \boldsymbol{c}_1 , \end{gather}

(3.6)\begin{gather}x_1 ={-}\left(\frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}}\right)^{{-}1} \left( \frac{\partial \boldsymbol{f}}{\partial \boldsymbol{c}} c_1 \right). \end{gather}

The second-order term gives

(3.7)\begin{gather} {0} = \frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}}\epsilon^2 \boldsymbol{x}_2 + \frac{1}{2}\frac{\partial^2 \boldsymbol{f}}{\partial \boldsymbol{x}^2}\epsilon^2 \boldsymbol{x}_1 \boldsymbol{x}_1 + \frac{1}{2}\frac{\partial^2 \boldsymbol{f}}{\partial \boldsymbol{c}^2}\epsilon^2 \boldsymbol{c}_1 \boldsymbol{c}_1 + \frac{\partial^2 \boldsymbol{f}}{\partial \boldsymbol{x}\partial \boldsymbol{c}}\epsilon^2 \boldsymbol{x}_1 \boldsymbol{c}_1 , \end{gather}

(3.8)\begin{gather}\boldsymbol{x}_2 ={-}\left(\frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}}\right)^{{-}1} \left( \frac{1}{2}\frac{\partial^2 \boldsymbol{f}}{\partial \boldsymbol{x}^2} \boldsymbol{x}_1 \boldsymbol{x}_1 + \frac{1}{2}\frac{\partial^2 \boldsymbol{f}}{\partial \boldsymbol{c}^2} \boldsymbol{c}_1 \boldsymbol{c}_1 + \frac{\partial^2 \boldsymbol{f}}{\partial \boldsymbol{x}\partial \boldsymbol{c}} \boldsymbol{x}_1 \boldsymbol{c}_1 \right) . \end{gather}

In general, the second-derivative terms will be large, dense, rank 3 tensors (recall that can be a vector-valued function), which may be extremely expensive to compute and may not even fit in memory for high-resolution cases. However, it is important to note that the full second derivatives are never needed (or indeed full first derivatives apart from the Jacobian matrix $\partial \boldsymbol {f}/\partial \boldsymbol {x}$). All that is needed are directional derivatives or Jacobian vector products. In the DESC code (§ 2) these are calculated using forward mode automatic differentiation at a cost a few times greater than the cost of a single evaluation of $\boldsymbol {f}$. These terms could also be approximated using finite differences at a similar cost. This means that at each order the most expensive operation is solving a linear system of the form

(3.9)\begin{equation} \boldsymbol{J} \boldsymbol{x}_i = \boldsymbol{b}, \end{equation}

where $\boldsymbol {J} \equiv \partial \boldsymbol {f} / \partial \boldsymbol {x}$ is the Jacobian matrix and is the same at each order, so only needs to be decomposed once, and $i$ is the order of the term in the perturbation series. Because of these computation and memory savings, the method has been extended to third order in the DESC code (see § 2), though in most situations first- or second-order perturbations give acceptable results (see figure 2).

It is instructive to note that the first-order term in the perturbation series for $\Delta \boldsymbol {x}$ is effectively the Newton step, while the second-order term is commonly referred to as the Halley step in optimization literature (Gander Reference Gander1985; Gundersen & Steihaug Reference Gundersen and Steihaug2010). While Newton's method converges quadratically (Nocedal & Wright Reference Nocedal and Wright2006) when started sufficiently close to a solution, if started far away it may diverge and so in practice the method must be globalized using either a line search or a trust region framework. Although we assume that we begin near or at an equilibrium so that $\boldsymbol {f}(\boldsymbol {x},\boldsymbol {c}) = 0$, depending on the size of the perturbation the solution landscape may change such that this is no longer the case, and we find in practice in several cases the unconstrained Newton step causes the solution to diverge. There is also an additional constraint inherent in the approach taken in that the second-order term should be smaller than the first-order term by a factor $\epsilon \ll 1$.

This suggests that a natural way to enforce these conditions and ensure reasonable convergence properties is to use a trust region method. When expanding the objective function in a Taylor series we are effectively approximating it by a linear or quadratic function. Instead of seeking the global minimizer to these model functions, the trust region approach instead recognizes that the Taylor approximation is only valid in some small neighbourhood and restricts the step size accordingly. Mathematically, instead of finding the exact solution $\boldsymbol {x}_i^*$ to the linear system

(3.10)\begin{equation} \boldsymbol{J} \boldsymbol{x}_i^* = \boldsymbol{b}, \end{equation}

we instead seek a solution to the following optimization problem:

(3.11)\begin{equation} \min_{\boldsymbol{x}_i} \|\boldsymbol{J} \boldsymbol{x}_i - \boldsymbol{b}\|^2 \quad {\rm s.t.}\ \|\boldsymbol{x}_i\| \le r, \end{equation}

where $r$ is the radius of the trust region. This subproblem has two possible solutions (Nocedal & Wright Reference Nocedal and Wright2006): either the true solution $\boldsymbol {x}_i^*$ lies within the trust region or else that there is a scalar $\alpha > 0$ such that

(3.12)\begin{equation} (\boldsymbol{J} + \alpha I)\boldsymbol{x}_i = \boldsymbol{b}, \quad \|\boldsymbol{x}_i\|=r. \end{equation}

The constrained value for $\boldsymbol {x}_i$ can be efficiently found using a one-dimensional root-finding method in $\alpha$. In the DESC code we use a bracketed Newton method. The cost of solving this subproblem is roughly the cost of one singular value decomposition of the Jacobian $\boldsymbol {J}$, or two to three Cholesky factorizations of the approximate Hessian matrix $\boldsymbol {B} \equiv \boldsymbol {J}^{\rm T} \boldsymbol {J}$.

Selection of the trust region radius $r$ is traditionally done adaptively within an optimization loop, by comparing the actual reduction in the residual at each step with that predicted by the model function. In a perturbation, only a single ‘step’ is taken, and we have found empirically that setting the trust region at a small fraction of $\|\boldsymbol {x}\|$ generally gives good results, typically $r=0.1 \|\boldsymbol {x}\|$. For second- and higher-order perturbations, such a large trust region can lead to inaccurate results. This can be understood by considering the expansion made in (3.2), where it was implicitly assumed that the second-order correction was a factor of $\epsilon$ smaller than the first-order term. Using a large trust region for the first-order term ($r=0.1 \|\boldsymbol {x}\|$) and a smaller trust region for the higher-order terms correctly enforces this assumed scaling. In practice we obtained good performance using $r_i=0.1 \|\boldsymbol {x}_{i-1}\|$, so the second-order term is an order of magnitude less than the first-order term and so on for higher orders.

4. Continuation method

Many MHD equilibrium codes (Hirshman & Whitson Reference Hirshman and Whitson1983a; Hudson et al. Reference Hudson, Dewar, Hole and McGann2012) use a multigrid approach, where an initial guess is specified on a coarse grid, and the error is minimized on that grid before being interpolated to a finer grid and re-solved, continuing until the finest resolution level has been reached. This is done both to speed computation by doing more calculations on coarser grids, and also to make it more robust to poor initial guesses and avoid additional saddle points that can appear in high-dimensional spaces (Dauphin et al. Reference Dauphin, Pascanu, Gulcehre, Cho, Ganguli and Bengio2014). DESC offers this as well, allowing the resolution to be varied in the radial, poloidal and toroidal directions independently.

In addition to the standard multigrid approach, DESC has also implemented a new continuation method using the perturbation techniques described in § 3. In general, continuation methods seek to find how the solution to an equation varies as parameters are changed. Using the notation of § 3 we can view $\boldsymbol {x}$ to be an implicit function of $\boldsymbol {c}$, related by the constraint equation $\boldsymbol {f}(\boldsymbol {x},\boldsymbol {c})=0$, and try to find the map that relates $\boldsymbol {x}$ and $\boldsymbol {c}$ along lines of $\boldsymbol {f}(\boldsymbol {x},\boldsymbol {c})=0$.

In this work, we note two properties that make continuation methods especially relevant:

1. (i) Two-dimensional (axisymmetric) equilibria are much easier to compute than 3-D equilibria, due to the guaranteed existence of flux surfaces in axisymmetric equilibria, and the significant reduction in the number of variables needed to represent the solution.

2. (ii) Vacuum (vanishing beta) equilibria are easier to compute than finite-pressure equilibria, due to the lack of Shafranov shift.

We can take advantage of these properties to compute complicated stellarator equilibria by first solving an ‘easy’ problem, and then introduce a continuation parameter that transforms our initial solution into the solution to a ‘hard’ problem.

To do this, we introduce two scalar continuation parameters: $\eta _b$, a multiplier on all of the non-axisymmetric boundary modes, and $\eta _p$, a scaling factor for the pressure profile. Setting $\eta _b=0$ would give a 2-D axisymmetric boundary that is ‘close’ to the desired 3-D equilibrium, while setting $\eta _p=0$ would give the zero pressure equilibrium with the desired boundary shape. By varying these two parameters, we find a ‘family’ of solutions that are connected continuously.

To vary the parameters, we apply a sequence of perturbation steps as outlined in § 3. With each perturbation we take a small step in the desired direction in parameter space (e.g. varying $\boldsymbol {c} = \{\eta _b, \eta _p\}$). Depending on the step size $\Delta \boldsymbol {c}$ it may be necessary to refine the solution with a small number (2–5) of Newton iterations of (2.1) to ensure a good equilibrium is reached. We then re-linearize about the new position and perform the next step, until the final desired parameters are reached.

A standard method for solving continuation problems, known as ‘natural parameter continuation’, would be analogous to a zeroth-order perturbation followed by several Newton iterations of (2.1), while a first-order perturbation would be similar to Gauss–Newton continuation. The higher-order perturbations discussed above do not seem to have been explored in the more general continuation method literature, but can be seen as a version of Halley's method applied to the combined system $\{\boldsymbol {f}(\boldsymbol {x},\boldsymbol {c})=0, \boldsymbol {c} - \boldsymbol {c}_{{\rm desired}}=0\}$.

In most traditional continuation methods, the step size in the continuation parameter is determined adaptively based on local error estimates and the ratio of predicted to achieved error reduction. In practice we have found that this is often not necessary, and fixing the step sizes a priori provides sufficiently accurate results. In most cases going from a zero-pressure equilibrium to a moderate beta of ${\sim }3\,\%$ can be done in a single step, and boundary perturbations in anywhere from one to four steps, depending on the desired accuracy and complexity of the boundary. This does require the user to specify the desired perturbation steps explicitly, though a future upgrade to the code is planned to allow adaptive perturbations where the user need only supply an initial guess and the final desired parameters.

As a first example (figure 1), we solve for a zero-pressure heliotron by first solving for a simple circular tokamak, then applying a 3-D perturbation to the boundary. After the perturbation, a small number of regular Newton iterations of (2.1) are applied to ensure convergence. As shown in figure 1 and table 1, the first order perturbation step captures the dominant effects of the shaping, while the second order correction has a smaller effect.

Figure 1. Comparison of perturbed tokamak equilibrium versus true solution for a heliotron-like stellarator. The initial tokamak (grey) is axisymmetric. By applying a perturbation (first order in red, second order in green) to the non-axisymmetric boundary modes, we obtain an approximation to the true 3-D solution (blue), obtained by solving from the start with the full 3-D boundary shape. The first-order perturbation captures the majority of the differences between the initial and true solutions. The second-order effects bring the perturbed solution even closer to the true one.

Table 1. Mean flux surface position error versus perturbation order for boundary perturbation from a circular tokamak to a heliotron.

Similarly, when computing finite-pressure equilibria it can be difficult to estimate the Shafranov shift a priori for generating a good initial guess. DESC avoids this by first computing a zero-pressure solution, for which a good initial guess can generally be found by simply scaling the boundary surface. The finite pressure is then added back in as a perturbation, which then often only requires a small number of further iterations to reach convergence as shown in figure 2. In these and the following examples, the rotational transform profile is held fixed during the perturbations, resulting in a change in the toroidal current as the pressure and boundary are varied. In this example, the toroidal current before and after (not shown) is largely similar, with a small amount of additional current required to support the increased pressure.

Figure 2. Comparison of perturbed equilibrium versus true solution for a change in pressure from $\beta =0\,\%$ to $\beta =3\,\%$. The first-order perturbation (red) captures the majority of the differences between the initial (grey) and true (blue) solutions. Second- and third-order effects (not shown for clarity) are visually very similar but significantly reduce the resulting force balance error as shown in table 2.

Table 2. Normalized force balance error versus perturbation order for a pressure increase from $\beta =0\,\%$ to $\beta =3\,\%$.

While in general the two parameters could be varied in any order, or simultaneously when solving for a 3-D finite-beta equilibrium, we have found that first varying $\eta _p$ followed by $\eta _b$ to be more efficient. Varying $\eta _p$ while holding $\eta _b$ fixed at $0$ allows the pressure perturbations to be done on a 2-D axisymmetric configuration, which reduces the computational cost and ensures the existence of good flux surfaces. After reaching a high-resolution finite-beta axisymmetric equilibrium, 3-D modes are added to the basis functions and the boundary is perturbed to give the final desired 3-D finite-beta equilibrium.

This procedure is demonstrated in figure 3, where the initial solution is an axisymmetric zero-pressure tokamak. The pressure is then increased, as demonstrated by the Shafranov shift, followed by 3-D deformation of the boundary shape to arrive at a W7-X-like configuration. After each large perturbation, a small number of regular Newton iterations of (2.1) are performed to ensure that an equilibrium has been reached (recall that in the derivation of the perturbations, it was assumed that the initial state before perturbing was an equilibrium). This method was also used to compute the solutions shown in Part 1 (Panici et al. Reference Panici, Conlin, Dudt and Kolemen2022), where a detailed analysis of the force error is given.

Figure 3. Continuation solution for W7-X-like equilibrium. Starting from a zero-pressure 2-D equilibrium, the pressure is increased to $\beta \sim 3\,\%$ in a series of two steps. Then a 3-D perturbation is applied to the boundary, broken up into four steps (two shown) to arrive at the final finite-beta 3-D solution.

Further insight can be gained by looking at the toroidal current profile of the W7-X-like equilibrium as the boundary ratio is varied in figure 4. At each step we keep the rotational transform profile fixed, and so as expected the axisymmetric case ($\eta _b=0$) requires a large toroidal current to generate the poloidal field. As we increase the 3-D shaping, more of the rotational transform is generated by axis torsion and boundary shaping, reducing the required plasma current to near zero.

Figure 4. Toroidal current and rotational transform for W7-X-like equilibrium with varying boundary ratios. When $\eta _b=0$, corresponding to an axisymmetric solution, a large toroidal current is required to generate the rotational transform (which is held fixed as the boundary is varied). Increasing the 3-D shaping allows more of the rotational transform to come from external fields, reducing the plasma current. Note that the current in the final step is still non-zero, as the rotational transform being held fixed was chosen for illustration, and does not correspond to the vacuum rotational transform on W7-X.

An important feature to note about the aforementioned continuation method is that the solution at each step (after any necessary Newton iterations of (2.1) to refine the solution) is in fact the ‘exact’ solution to the equilibrium problem with perturbed parameters, and is hence still a valid equilibrium that satisfies MHD force balance and may have desirable physics properties worth studying that may be absent in the final solution. By applying different perturbations and varying different parameters, one can explore whole families of solutions that are ‘nearby’ to a starting equilibrium.

5. Other applications

5.1. Parameter scans

Another important feature of continuation methods is revealing how solutions change as parameters of the problem are varied. In the previous section we used this to find single equilibria, but the method can also be used to explore families of equilibria related by a parameter or group of parameters. In this, we find equilibria ‘nearby’ to an equilibrium already found, such as examining the same boundary shape at different values of $\beta$ or boundary perturbations of varying magnitude and shape such as resonant magnetic perturbations in a tokamak. Traditionally this requires re-solving the equilibrium for each new value of the parameter. An alternative approach is to apply a perturbation to an initial equilibrium and find the corresponding changes in the flux surfaces. After applying the first perturbation, we re-linearize about the new state and perturb again, and so step through different equilibria for the cost of a single linear system solve at each step. This represents significant computational savings compared with solving the full nonlinear problem for each value of the parameter.

Figure 5 shows the flux surfaces on the $\zeta =0$ and $\zeta ={\rm \pi}$ planes for a helical stellarator for the same pressure profile scaled to different values of $\beta$. The initial solution was at $\beta = 0\,\%$, and second-order perturbations were applied sequentially to step the pressure up to $\beta =10\,\%$. As in previous examples, the rotational transform is held fixed as the pressure is increased, leading to an increase in the toroidal current. The flux surfaces are indistinguishable from those obtained by solving from scratch at each value of $\beta$, and the computational cost is significantly reduced, as shown in table 3. Performing such a scan requires only a few lines of code, as shown in Listing 1.

Listing 1 Code example for β scan.

Figure 5. Flux surfaces on the $\zeta =0$ and $\zeta ={\rm \pi}$ planes for a helical stellarator. The initial equilibrium had $\beta =0\,\%$, and a series of second-order perturbations were applied to increase the pressure rather than solving a new equilibrium from scratch each time.

Table 3. Computation times for different values of $\beta$ in the pressure scan shown in figure 5, both with and without perturbations, starting from a zero-pressure solution ($\beta =0$, not shown). The first perturbation takes longer as the time includes just-in-time compilation for the specific problem being solved, resulting in significantly faster times for the subsequent perturbation steps which reuse the same compiled code. The ‘without perturbations’ method is already able to take advantage of compiled code from the initial solve and does not see any significant speed-up at subsequent iterations. All computation was done on an AMD Ryzen 7 PRO 4750 U with 32 GB memory.

As another example (figure 6), a D-shaped tokamak was used as the starting point for variations in the rotational transform profile. The initial equilibrium had a rotational transform on axis of $\iota _0=1$, and perturbations were applied to reduce this down to $\iota _0=0.34$. As in the previous examples, the prescribed profiles at each step are pressure and rotational transform. As the rotational transform is decreased, we see increased Shafranov shift and deformation of the flux surfaces as the reduced poloidal field struggles to contain the pressure ($\beta \sim 3\,\%$ in this example).

Figure 6. Top: Flux surfaces on the $\zeta =0$ plane for a D-shaped tokamak with varying axis rotational transform. The initial equilibrium (blue) corresponds to $\iota _0=1$, and perturbations were used to reduce the axis rotational transform without recomputing the entire equilibrium solution. Bottom: Rotational transform profiles corresponding to flux surfaces shown above.

As in the pressure scan example, the solution obtained by perturbation is indistinguishable by eye from the solution obtained by solving the full equilibrium problem, and significantly faster. Once an initial equilibrium is solved, parameter scans can be performed an order of magnitude faster using perturbations than other approaches which require a full solution at each step. The code to perform such a scan is shown in Listing 2.

Listing 2 Code example for perturbing ɩ profile.

5.2. Optimization

The perturbation techniques described previously can also be adapted for optimization, where instead of choosing a particular change in the parameters $\Delta \boldsymbol {c}$ we instead let $\Delta \boldsymbol {c}$ be a free parameter that is chosen to minimize a cost function $\boldsymbol {g}(\boldsymbol {x},\boldsymbol {c})$, such as quasi-symmetry error (Boozer Reference Boozer1983; Helander Reference Helander2014), coil complexity (Zhu et al. Reference Zhu, Hudson, Song and Wan2018b, Reference Zhu, Hudson, Lazerson, Song and Wan2018a; McGreivy, Hudson & Zhu Reference McGreivy, Hudson and Zhu2020) or fast particle confinement (Nemov et al. Reference Nemov, Kasilov, Kernbichler and Leitold2008; Velasco et al. Reference Velasco, Calvo, Mulas, Sanchez, Parra and Cappa2021):

(5.1)\begin{equation} \Delta \boldsymbol{c}^* = {\rm arg\,min}_{\Delta \boldsymbol{c}} \boldsymbol{g}(\boldsymbol{x}+\Delta \boldsymbol{x}, \boldsymbol{c} + \Delta \boldsymbol{c}) \quad {\rm s.t.}\ \boldsymbol{f}(\boldsymbol{x}+\Delta \boldsymbol{x}, \boldsymbol{c}+\Delta \boldsymbol{c}) = 0, \end{equation}

where as before $\Delta \boldsymbol {x}$ is an implicit function of $\Delta \boldsymbol {c}$.

This finds the step in parameter space that most decreases the cost function $\boldsymbol {g}$ while maintaining approximate force balance. After applying this perturbation step, a small number of Newton iterations of (2.1) are used to reconverge to the correct equilibrium, without the need for a full ‘cold start’ equilibrium solve. This single ‘warm start’ equilibrium solve in DESC can be contrasted with the method of STELLOPT (Lazerson et al. Reference Lazerson, Schmitt, Zhu and Breslau2020) or SIMSOPT (Landreman et al. Reference Landreman, Medasani, Wechsung, Giuliani, Jorge and Zhu2021) where at each optimization step a series of $N$ cold start equilibrium solves must be performed to find the descent direction, where $N$ is the number of variables being optimized.

In the optimization literature, this is part of a more general class of methods for constrained optimization. Like the perturbations described in § 3, this method can also be extended to higher order. This extension and further details of this method of optimization and applications to quasi-symmetry are given in Part 3 (Dudt et al. Reference Dudt, Conlin, Panici and Kolemen2022).