Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-23T11:00:31.308Z Has data issue: false hasContentIssue false
  • English
  • Français

On the electric field components in the collisionless plasmoid instability

Published online by Cambridge University Press:  15 February 2022

M. Shahraki Pour  and
M. Hosseinpour Open the ORCID record for M. Hosseinpour [Opens in a new window]
M. Shahraki Pour
Affiliation:
Faculty of Physics, University of Tabriz, PO Box 16471, Tabriz, Iran
M. Hosseinpour*
Affiliation:
Faculty of Physics, University of Tabriz, PO Box 16471, Tabriz, Iran
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Using two-dimensional particle-in-cell simulations of collsionless plasmoid instability, the spatial and temporal variations of electric field components are investigated. The initial magnetic field is a Harris sheet which is added by a non-uniform perpendicular magnetic field (guide field). The effects of weak and medium guide field on the evolution of plasmoid instability and associated electric field are discussed with the input parameters of the solar corona with the condition $\omega _{{\rm pe}}/\omega _{{\rm ce}}>1$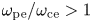. As the current sheet elongates, magnetic reconnection in an X-point transits into the plasmoid instability, in which secondary X-points are formed and the consequent magnetic islands coalesce and form larger islands. During the instability, electric field components show two types of disturbances. (1) Transient waves, being excited very early, propagate mainly perpendicular to the current sheet and become damped as the instability proceeds to the nonlinear stage. Fourier analysis reveals that electromagnetic right- and left-hand polarized modes parallel to the initial magnetic field and also the extraordinary mode perpendicular to the current sheet are excited. Additionally, electron Langmuir and slow magnetosonic waves are observed in both directions. (2) Inside the current sheet, an electric field is generated by the plasmoid-dominated reconnection and grows in amplitude as the plasmoid instability proceeds. Moreover, in our study, the effects of amplitude-varying guide field on the spatial structure of electric field components outside and inside the current sheet are discussed. This study is valuable because understanding the spatial and temporal variation of the electric field is an essential prerequisite for the issue of particle acceleration in plasmoid-dominated magnetic reconnection.

Keywords

astrophysical plasmasplasma simulationplasma waves
Type
Research Article
Information
Journal of Plasma Physics , Volume 88 , Issue 1 , February 2022 , 905880113
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bárta, M., Büchner, J., Karlický, M. & Kotrč, P. 2011 Spontaneous current-layer fragmentation and cascading reconnection in solar flares: II. Relation to observations. Astrophys. J. 730, 47.CrossRefGoogle Scholar
Bhattacharjee, A. 2004 Impulsive magnetic reconnection in the Earth's magnetotail and the solar corona. Annu. Rev. Astron. Astrophys. 42, 365.CrossRefGoogle Scholar
Bhattacharjee, A., Brunel, F. & Tajima, T. 1983 Magnetic reconnection driven by the coalescence instability. Phys. Fluids 26, 3332.CrossRefGoogle Scholar
Birn, J. & Priest, E. 2007 Reconnection of Magnetic Fields: Magnetohydrodynamic and Collisionless Theory and Observations. Cambridge University Press.CrossRefGoogle Scholar
Cargill, P.J., Vlahos, L., Baumann, G., Drake, J.F. & Nordlund, Å. 2012 Current fragmentation and particle acceleration in solar flares. Space Sci. Rev. 173, 223.CrossRefGoogle Scholar
Chen, L.J., Daughton, M., Bhattacharjee, A., Torbert, R.B., Roytershteyn, V. & Bessho, N. 2012 In-plane electric fields in magnetic islands during collisionless magnetic reconnection. Phys. Plasmas 19, 112902.CrossRefGoogle Scholar
Comisso, L., Lingam, M., Huang, Y.-M. & Bhattacharjee, A. 2016 General theory of the plasmoid instability. Phys. Plasmas 23, 100702.CrossRefGoogle Scholar
Comisso, L., Lingam, M., Huang, Y.-M. & Bhattacharjee, A. 2017 Plasmoid instability in forming current sheets. Astrophys. J. 850, 142.CrossRefGoogle Scholar
Daughton, W., Roytershteyn, V., Albright, B.J., Karimabadi, H., Yin, L. & Bowers, K.J. 2009 Role of electron physics in the development of turbulent magnetic reconnection in collisionless plasmas. Phys. Rev. Lett. 103, 065004.CrossRefGoogle Scholar
Drake, J.F., Swisdak, M., Schoeffler, K.M., Rogers, B.N. & Kobayashi, S. 2006 Formation of secondary islands during magnetic reconnection. Geophys. Res. Lett. 33, L13105.CrossRefGoogle Scholar
Egedal, J., Daughton, W. & Le, A. 2012 Large-scale electron acceleration by parallel electric fields during magnetic reconnection. Nat. Phys. 8, 321.CrossRefGoogle Scholar
Fan, F., Huang, C., Lu, Q., Xie, J. & Wang, S. 2016 The structures of magnetic islands formed during collisionless magnetic reconnections in a force-free current sheet. Phys. Plasmas 23, 112106.CrossRefGoogle Scholar
Fu, S., Huang, S., Zhou, M., Ni, B. & Deng, X. 2018 Tripolar electric field structure in guide field magnetic reconnection. Ann. Geophys. 36, 373.CrossRefGoogle Scholar
Galsgaard, K. & Nordlund, Å. 1996 Heating and activity of the solar corona: 1. Boundary shearing of an initially homogeneous magnetic field. J. Geophys. Res. 101, 13445.CrossRefGoogle Scholar
Gonzalez, W. & Parker, E. 2016 Magnetic Reconnection Concepts and Applications. Springer.CrossRefGoogle Scholar
Gudiksen, B.V. & Nordlund, Å. 2005 An ab initio approach to the solar coronal heating problem. Astrophys. J. 618, 1020.CrossRefGoogle Scholar
Intrator, T.P., Sun, X., Lapenta, G., Dorf, L. & Furno, I. 2009 Experimental onset threshold and magnetic pressure pile-up for 3D reconnection. Nat. Phys. 5, 521.CrossRefGoogle Scholar
Karimabadi, H., Dorelli, J., Roytershteyn, V., Daughton, W. & Chacon, L. 2011 Flux pileup in collisionless magnetic reconnection: bursty interaction of large flux ropes. Phys. Rev. Lett. 107, 025002.CrossRefGoogle ScholarPubMed
Karimabadi, H., Krauss-Varban, D. & Omidi, N. 1999 Magnetic structure of the reconnection layer and core field generation in plasmoids. J. Geophys. Res. 104, 12313.CrossRefGoogle Scholar
Kumar, P., Karpen, J.T., Antiochos, S.K., Wyper, P.F. & Devore, C.R. 2019 First detection of plasmoids from breakout reconnection on the Sun. Astrophys. J. Lett. 885, L15.CrossRefGoogle Scholar
Liu, W., Chen, Q. & Petrosian, V. 2013 Plasmoid ejections and loop contractions in an eruptive M7.7 solar flare: evidence of particle acceleration and heating in magnetic reconnection outflows. Astrophys. J. 767, 168.CrossRefGoogle Scholar
Loureiro, N.F., Schekochihin, A.A. & Cowley, S.C. 2007 Instability of current sheets and formation of plasmoid chains. Phys. Plasmas 14, 100703.CrossRefGoogle Scholar
Markidis, S., Henri, P., Lapenta, G., Divin, A., Goldman, M.V., Newman, D. & Eriksson, S. 2012 Collisionless magnetic reconnection in a plasmoid chain. Nonlinear Process. Geophys. 19, 145.CrossRefGoogle Scholar
Priest, E. & Forbes, T. 2000 Magnetic Reconnection: MHD Theory and Applications. Cambridge University Press.CrossRefGoogle Scholar
Wan, W., Lapenta, G., Delzanno, G.L. & Egedal, J. 2008 Electron acceleration during guide field magnetic reconnection. Phys. Plasmas 15, 032903.CrossRefGoogle Scholar
Yamada, M., Kulsrud, R. & Ji, H. 2010 Magnetic reconnection. Rev. Mod. Phys. 82, 603.CrossRefGoogle Scholar
Zhou, M., Deng, X.H. & Huang, S.Y. 2012 Electric field structure inside the secondary island in the reconnection diffusion region. Phys. Plasmas 19, 042902.CrossRefGoogle Scholar