The magnetized plasma-wall transition (MPWT) layer occurring, for example near a tokamak diverter, typically consists of three distinct sublayers: the Debye sheath (DS), the magnetic presheath (MPS) and the collisional presheath (CPS), with characteristic lengths λD (electron Debye length), ρi (ion gyroradius) and λ (smallest relevant ion collision length), respectively. For analytical simplicity one usually assumes the ordering λD ≪ ρi ≪ λ, or, equivalently, 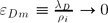and 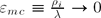(‘asymptotic three-scale (A3S) limit’), in which the three sublayers are precisely defined. In the present work the equations and length scales governing the transition, or the ‘intermediate’ regions between neighboring sublayers (DS–MPS, MPS–CPS), in the A3S limit are derived, allowing one to avoid the singularities arising from the ϵDm → 0 and ϵmc → 0 approximations. The MPS entrance and the related Bohm–Chodura condition is defined in a natural way. It is found that in the hydrodynamic Ti = 0 approximation the intermediate scales and equations have a universal form and a similar structure not only for the MPS–DS and CPS–MPS transitions but also for the DS–CPS transition in the non-magnetized case.