Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-23T14:41:44.733Z Has data issue: false hasContentIssue false
  • English
  • Français

How eigenmode self-interaction affects zonal flows and convergence of tokamak core turbulence with toroidal system size

Part of: Focus on Fusion

Published online by Cambridge University Press:  28 September 2020

Ajay C. J. Open the ORCID record for Ajay C. J. [Opens in a new window] ,
Stephan Brunner Open the ORCID record for Stephan Brunner [Opens in a new window] ,
Ben McMillan Open the ORCID record for Ben McMillan [Opens in a new window] ,
Justin Ball Open the ORCID record for Justin Ball [Opens in a new window] ,
Julien Dominski Open the ORCID record for Julien Dominski [Opens in a new window]  and
Gabriele Merlo
Ajay C. J.*
Affiliation:
Ecole Polytechnique Fédérale de Lausanne (EPFL), Swiss Plasma Center, CH-1015Lausanne, Switzerland
Stephan Brunner
Affiliation:
Ecole Polytechnique Fédérale de Lausanne (EPFL), Swiss Plasma Center, CH-1015Lausanne, Switzerland
Ben McMillan
Affiliation:
Centre for Fusion, Space and Astrophysics, Department of Physics, University of Warwick, CV4 7ALCoventry, UK
Justin Ball
Affiliation:
Ecole Polytechnique Fédérale de Lausanne (EPFL), Swiss Plasma Center, CH-1015Lausanne, Switzerland
Julien Dominski
Affiliation:
Princeton Plasma Physics Laboratory, Princeton University, P.O. Box 451, Princeton, NJ08543-0451, USA
Gabriele Merlo
Affiliation:
The University of Texas at Austin, Austin, TX78712, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

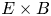Self-interaction is the process by which a microinstability eigenmode that is extended along the direction parallel to the magnetic field interacts non-linearly with itself. This effect is particularly significant in gyrokinetic simulations accounting for kinetic passing electron dynamics and is known to generate stationary $E\times B$ zonal flow shear layers at radial locations near low-order mode rational surfaces (Weikl et al. Phys. Plasmas, vol. 25, 2018, 072305). We find that self-interaction, in fact, plays a very significant role in also generating fluctuating zonal flows, which is critical to regulating turbulent transport throughout the radial extent. Unlike the usual picture of zonal flow drive in which microinstability eigenmodes coherently amplify the flow via modulational instabilities, the self-interaction drive of zonal flows from these eigenmodes are uncorrelated with each other. It is shown that the associated shearing rate of the fluctuating zonal flows therefore reduces as more toroidal modes are resolved in the simulation. In simulations accounting for the full toroidal domain, such an increase in the density of toroidal modes corresponds to an increase in the toroidal system size, leading to a finite system size effect that is distinct from the well-known profile shearing effect.

Keywords

fusion plasmaplasma simulationplasma non-linear phenomena
Type
Research Article
Information
Journal of Plasma Physics , Volume 86 , Issue 5 , October 2020 , 905860504
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abiteboul, J. 2012 Turbulent and neoclassical toroidal momentum transport in tokamak plasmas. PhD thesis, Aix-Marseille Université.Google Scholar
Abiteboul, J., Garbet, X., Grandgirard, V., Allfrey, S. J., Ghendrih, Ph., Latu, G., Sarazin, Y. & Strugarek, A. 2011 Conservation equations and calculation of mean flows in gyrokinetics. Phys. Plasmas 18 (8), 082503.Google Scholar
Ball, J., Brunner, S. & C. J., Ajay 2020 Eliminating turbulent self-interaction through the parallel boundary condition in local gyrokinetic simulations. J. Plasma Phys. 86 (2), 905860207.CrossRefGoogle Scholar
Beer, M. A., Cowley, S. C. & Hammett, G. W. 1995 Field-aligned coordinates for nonlinear simulations of tokamak turbulence. Phys. Plasmas 2 (7), 2687–2700.CrossRefGoogle Scholar
Biglari, H., Diamond, P. H. & Terry, P. W. 1990 Influence of sheared poloidal rotation on edge turbulence. Phys. Fluids B 2 (1), 1–4.CrossRefGoogle Scholar
Candy, J., Belli, E. A. & Staebler, G. 2020 Spectral treatment of gyrokinetic profile curvature. Plasma Phys. Control. Fusion 62 (4), 042001.CrossRefGoogle Scholar
Chen, L., Lin, Z. & White, R. 2000 Excitation of zonal flow by drift waves in toroidal plasmas. Phys. Plasmas 7 (8), 3129–3132.CrossRefGoogle Scholar
Chowdhury, J., Ganesh, R., Angelino, P., Vaclavik, J., Villard, L. & Brunner, S. 2008 Role of non-adiabatic untrapped electrons in global electrostatic ion temperature gradient driven modes in a tokamak. Phys. Plasmas 15 (7), 072117.CrossRefGoogle Scholar
Connor, J. W., Hastie, R. J. & Taylor, J. B. 1978 Shear, periodicity, and plasma ballooning modes. Phys. Rev. Lett. 40, 396–399.Google Scholar
Diamond, P. H., Itoh, S.-I., Itoh, K. & Hahm, T. S. 2005 Zonal flows in plasma – a review. Plasma Phys. Control. Fusion 47 (12A), R35.Google Scholar
Dimits, A. M., Bateman, G., Beer, M. A., Cohen, B. I., Dorland, W., Hammett, G. W., Kim, C., Kinsey, J. E., Kotschenreuther, M., Kritz, A. H., et al. 2000 Comparisons and physics basis of tokamak transport models and turbulence simulations. Phys. Plasmas 7 (3), 969–983.CrossRefGoogle Scholar
Dominski, J., Brunner, S., Görler, T., Jenko, F., Told, D. & Villard, L. 2015 How non-adiabatic passing electron layers of linear microinstabilities affect turbulent transport. Phys. Plasmas 22 (6), 062303.CrossRefGoogle Scholar
Dominski, J., McMillan, B. F., Brunner, S., Merlo, G., Tran, T.-M. & Villard, L. 2017 An arbitrary wavelength solver for global gyrokinetic simulations. Application to the study of fine radial structures on microturbulence due to non-adiabatic passing electron dynamics. Phys. Plasmas 24 (2), 022308.CrossRefGoogle Scholar
Dorland, W., Jenko, F., Kotschenreuther, M. & Rogers, B. N. 2000 Electron temperature gradient turbulence. Phys. Rev. Lett. 85, 5579–5582.CrossRefGoogle ScholarPubMed
Faber, B. J., Pueschel, M. J., Terry, P. W., Hegna, C. C. & Roman, J. E. 2018 Stellarator microinstabilities and turbulence at low magnetic shear. J. Plasma Phys. 84 (5), 905840503.CrossRefGoogle Scholar
Falchetto, G. L., Vaclavik, J. & Villard, L. 2003 Global-gyrokinetic study of finite $\beta$ effects on linear microinstabilities. Phys. Plasmas 10 (5), 1424–1436.Google Scholar
Gallagher, S., Hnat, B., Connaughton, C., Nazarenko, S. & Rowlands, G. 2012 The modulational instability in the extended Hasegawa–Mima equation with a finite larmor radius. Phys. Plasmas 19 (12), 122115.CrossRefGoogle Scholar
Görler, T., Lapillonne, X., Brunner, S., Dannert, T., Jenko, F., Merz, F. & Told, D. 2011 The global version of the gyrokinetic turbulence code gene. J. Comput. Phys. 230 (18), 7053–7071.CrossRefGoogle Scholar
Hahm, T. S., Beer, M. A., Lin, Z., Hammett, G. W., Lee, W. W. & Tang, W. M. 1999 Shearing rate of time-dependent $E\times B$ flow. Phys. Plasmas 6 (2–3), 922–926.CrossRefGoogle Scholar
Hallatschek, K. & Dorland, W. 2005 Giant electron tails and passing electron pinch effects in tokamak-core turbulence. Phys. Rev. Lett. 95, 055002.CrossRefGoogle ScholarPubMed
Hasegawa, A., Maclennan, C. G. & Kodama, Y. 1979 Nonlinear behavior and turbulence spectra of drift waves and Rossby waves. Phys. Fluids 22 (11), 2122–2129.Google Scholar
Hasegawa, A. & Mima, K. 1978 Pseudo-three-dimensional turbulence in magnetized nonuniform plasma. Phys. Fluids 21 (1), 87–92.CrossRefGoogle Scholar
Hatch, D. R., Terry, P. W., Jenko, F., Merz, F. & Nevins, W. M. 2011 Saturation of gyrokinetic turbulence through damped eigenmodes. Phys. Rev. Lett. 106, 115003.CrossRefGoogle ScholarPubMed
Hazeltine, R. D. & Newcomb, W. A. 1990 Inversion of the ballooning transformation. Phys. Fluids B 2 (1), 7–10.Google Scholar
Horton, W. 1999 Drift waves and transport. Rev. Mod. Phys. 71, 735–778.CrossRefGoogle Scholar
Jenko, F., Dorland, W., Kotschenreuther, M. & Rogers, B. N. 2000 Electron temperature gradient driven turbulence. Phys. Plasmas 7 (5), 1904–1910.CrossRefGoogle Scholar
Krommes, J. A. & Kim, C.-B. 2000 Interactions of disparate scales in drift-wave turbulence. Phys. Rev. E 62, 8508–8539.CrossRefGoogle ScholarPubMed
Lapillonne, X., Brunner, S., Dannert, T., Jolliet, S., Marinoni, A., Villard, L., Gorler, T., Jenko, F. & Merz, F. 2009 Clarifications to the limitations of the s-alpha equilibrium model for gyrokinetic computations of turbulence. Phys. Plasmas 16 (3), 032308.CrossRefGoogle Scholar
Lin, Z., Hahm, T. S., Lee, W. W., Tang, W. M. & White, R. B. 1998 Turbulent transport reduction by zonal flows: massively parallel simulations. Science 281 (5384), 1835–1837.CrossRefGoogle ScholarPubMed
McMillan, B., Lapillonne, X., Brunner, S., Villard, L., Jolliet, S., Bottino, A., Goerler, T. & Jenko, F. 2010 System size effects on gyrokinetic turbulence. Phys. Rev. Lett. 105, 155001.CrossRefGoogle ScholarPubMed
Merz, F. 2008 Gyrokinetic simulation of multimode plasma turbulence. PhD thesis, Universität Münster.Google Scholar
Parra, F. I. & Catto, P. J. 2009 Vorticity and intrinsic ambipolarity in turbulent tokamaks. Plasma Phys. Control. Fusion 51 (9), 095008.CrossRefGoogle Scholar
Rosenbluth, M. N. & Hinton, F. L. 1998 Poloidal flow driven by ion-temperature-gradient turbulence in tokamaks. Phys. Rev. Lett. 80, 724–727.CrossRefGoogle Scholar
Scott, B. 1998 Global consistency for thin flux tube treatments of toroidal geometry. Phys. Plasmas 5 (6), 2334–2339.CrossRefGoogle Scholar
Waltz, R. E. 2005 Rho-star scaling and physically realistic gyrokinetic simulations of transport in DIII-D. Fusion Sci. Technol. 48 (2), 1051–1059.CrossRefGoogle Scholar
Waltz, R. E., Austin, M. E., Burrell, K. H. & Candy, J. 2006 Gyrokinetic simulations of off-axis minimum-q profile corrugations. Phys. Plasmas 13 (5), 052301.CrossRefGoogle Scholar
Waltz, R. E., Candy, J. M. & Rosenbluth, M. N. 2002 Gyrokinetic turbulence simulation of profile shear stabilization and broken gyrobohm scaling. Phys. Plasmas 9 (5), 1938–1946.CrossRefGoogle Scholar
Waltz, R. E., Dewar, R. L. & Garbet, X. 1998 Theory and simulation of rotational shear stabilization of turbulence. Phys. Plasmas 5 (5), 1784–1792.CrossRefGoogle Scholar
Waltz, R. E., Kerbel, G. D. & Milovich, J. 1994 Toroidal Gyro-Landau fluid model turbulence simulations in a nonlinear ballooning mode representation with radial modes. Phys. Plasmas 1 (7), 2229–2244.CrossRefGoogle Scholar
Weikl, A., Peeters, A. G., Rath, F., Seiferling, F., Buchholz, R., Grosshauser, S. R. & Strintzi, D. 2018 The occurrence of staircases in ITG turbulence with kinetic electrons and the zonal flow drive through self-interaction. Phys. Plasmas 25 (7), 072305.CrossRefGoogle Scholar