Introduction
The threshold wind—speed, at which particle motion just begins, is a critical parameter of any accurate formulation that expresses the transport rate of heavy particles such as sand, soil, or snow as a function of horizontal wind—speed in the Earth’s atmosphere. Until the wind reaches this threshold speed, no transport occurs. But the characteristics of particles, surface, and wind that determine the threshold speed, continue to govern the relationship between wind and particle mass flux as speed increases above the threshold. Therefore, this critical value represents something of an index for the effectiveness of the wind in particle transport at all speeds.
Wind, at speeds near the threshold for particle movement, is classified as turbulent flow over a rough surface, with the possible exception of wind moving scattered particles on very smooth ice. Threshold wind—speeds are usually reported as values measured at a specified height, averaged for some specific time period, but the maxima or gusts during the period actually initiate particle motion. Momentum is transferred to the surface by these horizontal velocity maxima and the associated vertical component of the turbulent wind. The vertical wind—speed profile determines friction velocity, defined by U ★ = (τ0/ρa)½ where τo is the surface shear stress and air density is ρa.
Blowing—snow particles are usually fragments of the original precipitation crystals, except for those being transported by wind during snow—fall. Once on the surface, snow crystals become bonded to other crystals so rapidly that the wind has little chance to move these relatively large particles. Particles moving very near the surface range from a few to 800 μm or more with mean sizes about 200 μm and the distribution of sizes reasonably well described by the two—parameter gamma function (Reference Budd and RubinBudd, 1966). For a surface of snow that fell during calm conditions, close—up photographs show snow crystals interlocked to such an extent that only small portions of the uppermost crystals receive the main impact of horizontal wind component. These protrusions must be broken from the snow crystal to initiate transport. When wind restarts movement of an old snow surface, protrusions at the surface are usually much less fragile. If snow was deposited from wind transport, the particles are typically small ice grains, and cohesive bonds between these must be broken to start movement again. When particle movement starts again, bond strength has increased so that interparticle bonds cannot be broken by wind forces that initiated previous transport, and higher threshold speeds, or other forces, are required.
Surface features determine the distribution of wind shear stress, concentrating the force of horizontal wind gusts on the frontal areas of ripples, ridges, dunes, and sastrugi. Since these features result from previous transport, and are aligned according to that wind direction, the threshold for reinitiating transport depends on the new wind direction and may be less than the threshold along the previous wind direction. Perhaps the most important interaction of surface features with drifting is their influence on trajectories, as particles rebound from the windward faces. The effect of surface features needs further study.
In defining the threshold wind—speed for snow movement, it is particularly important to maintain the differentiation made by Bagnold (1941, p. 265) between the “fluid” and “impact” thresholds. For motion of a sand bed with mixed grain sizes, he noted that as the fluid forces became large enough, small grains were removed from the surface, after which the bed was stable at that wind—speed. With another small increase in speed, the next larger size of grains were moved, and so on, until only the largest sizes remained exposed on the surface. Above this velocity, motion of the bed is continuous. For dry quartz sand, the “fluid” threshold is the velocity at which aerodynamic forces overcome the force due to weight of the grain, and thus is a well—defined function of grain size.
The characteristic motion of particles by jumps, referred to as saltation, creates additional forces when moving particles impact those at rest on the surface. If a sand surface is disturbed artificially so that saltation begins, then the wind—speed at which motion will just be maintained down—wind is lower than the fluid threshold. Bagnold found that this “impact” threshold also depended on the same (square—root) function of grain size, but velocities were 20% lower than the fluid thresholds.
In the ease of snow, cohesive forces are usually much larger than the force associated with particle mass, and the strength of intergranular bonds is strongly time and temperature dependent. Instead of a well—defined relation of threshold speed and particle size, the situation is more complicated because large differences between fluid and impact threshold develop: The fluid threshold for movement of old snow surfaces appears to increase beyond the range of natural wind. Erosion of snow surfaces with high fluid thresholds by much lower wind speeds and precipitating ice crystals demonstrates the difference between the forces of fluid drag on a surface particle, and elastic impact of a saltating particle.
As with most problems that concern the structure of natural snow, simplifying assumptions are necessary to start an analysis. Therefore most of the mathematical arguments that follow deal with spherical particles of ice instead of the irregular fragments that are real particles of blowing snow.
Fluid forces on a surface particle
To determine the relevant features of particle and wind interaction that combine to dictate the wind speed at which particle motion begins, it will help to examine the forces on a particle exposed to the wind on a horizontal bed of particles. The analysis for sand presented by Bagnold (1941, p. 265) provides a beginning. Reference ChepilChepil’s (1959) work with soil expands the analysis, to which must be added those factors peculiar to snow, to arrive at a mathematical formulation of the forces. This should help perception of the factors represented by windspeed values at the fluid threshold.
The analysis for sand
Bagnold (1941, p. 265) equated the moment of the particle’s immersed weight acting through its center of gravity, with the force exerted by the wind against the projected area of the particle to arrive at the forces on an exposed sand grain at the fluid threshold. He assumed the wind force was proportional to the square of friction velocity U* to derive the equation
where g is the gravitational acceleration, ρ a and ρ p are air and particle density, and A is a coefficient of proportionality. Since by definition, (
and for sand or snow particles in air ρ p is at least a thousand times larger than ρ a, so
According to Bagnold, the coefficient A depends on the ratio of the maximum momentary velocities of turbulence to the mean velocity, also on the proportion of the drag per unit area which is taken by a particle, by virtue of its relative position in the piling, and partly on the height at which the drag force acts. For sand grains larger than 250 μm in diameter, his experiments in the wind tunnel gave A = 0.1 for the “fluid” threshold. For smaller grains (less than 100 μm diameter) the coefficient increased.
Chepil’s (1945[a], [b]) wind—tunnel experiment confirmed the analysis and the value of the coefficient A for soil grains, where the particle densities varied from 1.6 to 2.0 Mg m—3. Reference Zinggzingg (1953) determined the value for the “saltation” threshold of sand to be A = 0.116, where the critical shear stress was estimated by a graphical technique rather than visual observation. Chepil continued experiments directed toward evaluating those factors (noted by Bagnold) upon which coefficient A depends. His ingenuity and willingness to undertake difficult measurements can be seen from the experimental determination he made of lift and drag on a single surface soil particle. These efforts culminated in the analysis outlined below (Reference ChepilChepil, 1959), which refers to an exposed soil grain at rest on a bed of soil particles and the fluid forces acting on the grain.
Moments due to forces acting on the grain (Fig. 1) are computed for motion around the down—wind contact point, P. Thus, grain weight acts through the center of gravity, and the moment arm X is estimated from the angle of repose determined by tilting the bed until grain motion occurs. For dune sand of various sizes, the angle is almost constant at 33°. This force is directly opposed by the lift L c created by the Bernoulli effect. Measurements showed L c was consistently about 0.85 times the total drag force F e (Reference ChepilChepil, 1958). The moment arm X/tan Φ' through which F e acts, is determined by the distribution of velocity pressure on the exposed grain. Integration of drag due to fluid velocity determined the level at which one—half the drag acted above and one—half below. This average drag level determined the angle Φ’ (240 from the average of Chepil’s calculations), and the balance of moments gives an expression for the critical drag force:

Fig. 1. Diagram for the analysis of fluid forces on a surface particle without cohesion (after Reference ChepilChepil, 1959).
Substituting L c = 0.85Fc and factoring gives
the critical drag force required to move a particle of diameter d, assuming it has the mass of a sphere of density ρ', equal to the difference between the particle and fluid densities ρ' = (ρp—ρa). The horizontal area over which this drag can be distributed is the projected area of the grain (assumed spherical) or 0.785 4d 2 so that drag per unit area on the most exposed grains is estimated by
The critical drag per unit area of the horizontal bed τc, is expected to be in some ratio η to the drag that moves the top grains so that τc/Fe' = η and
Chepil evaluated this packing ratio η from experiments with hemispheres of three sizes spaced in a hexagonal pattern, three diameters apart. The values show only a slight effect of size and no trend with wind—speed, so that the average η = 0.21 is used in his computations.
The final factor in Chepil’s analysis is the ratio T of maximum to mean turbulent impulse. He assumes this ratio to be the same for both lift and drag forces, so that the mean critical drag ![]() per unit area of the whole bed is τc = T and
per unit area of the whole bed is τc = T and
In terms of a threshold friction velocity, U*t = (

or

Pressure fluctuations that produce both lift and drag, measured at the level of the most exposed grains by Reference ChepilChepil and Siddoway (1959), showed a “somewhat skewed normal error law”. This is noteworthy in view of the skewness shown in recent wind—tunnel measurements of turbulent shear stress (Pyle, unpublished). Values for T were approximated from the ratio (P+3σp)/P where P is the mean and σp represents the standard deviation of the measured pressure fluctuations.
Chepil’s analysis tends to overestimate threshold drag ![]() by a consistent percentage (Fig 2) for both sand and soil particles, but it appears that effects of turbulent gusts, grain exposure, and packing have been taken into account in a reasonable way. Out of curiosity, assume a bed of ice grains similar in shape to quartz sand with a uniform size d = 0.2 mm. If these particles have density ρp = 0.9 Mg/m3, and are only held on the surface by their weight, at what value of friction velocity would movement begin according to Chepil’s analysis? Evaluating Equation (7), using his values η = 0.21, Φ'= 24°, T = 2.5, and ρa = 0.001 Mg/m3, gives U*t = 24 cm/s. The critical force due to drag, calculated for the above situation by Equation (3), is F c = 0.001 2 dyn (1.2 x 1o—8 N), roughly one—thousandth the weight of a cubic centimeter of air.
by a consistent percentage (Fig 2) for both sand and soil particles, but it appears that effects of turbulent gusts, grain exposure, and packing have been taken into account in a reasonable way. Out of curiosity, assume a bed of ice grains similar in shape to quartz sand with a uniform size d = 0.2 mm. If these particles have density ρp = 0.9 Mg/m3, and are only held on the surface by their weight, at what value of friction velocity would movement begin according to Chepil’s analysis? Evaluating Equation (7), using his values η = 0.21, Φ'= 24°, T = 2.5, and ρa = 0.001 Mg/m3, gives U*t = 24 cm/s. The critical force due to drag, calculated for the above situation by Equation (3), is F c = 0.001 2 dyn (1.2 x 1o—8 N), roughly one—thousandth the weight of a cubic centimeter of air.
The analysis for snow
Although snow particles are more irregular than sand, especially new snow on the surface before drift begins, the largest difference between the forces on snow particles at fluid threshold, and those on sand is the greater prevalence of cohesive forces. Rain will immobilize a sand surface by producing cohesion between grains, but the natural tendency in desert regions is away from this condition, toward lower threshold values. Metamorphism of snow, in contrast, usually tends to increase threshold wind—speed values as grain size and cohesion become larger. An attempt is made, in this section, to add to Chepil’s analysis the cohesive forces on a particle. These may be considered as the combined force required to overcome both intergranular bonds and electrostatic forces, but in evaluating the result, only mechanical bond strength will be considered.

Fig. 2. Threshold drag as a function of particle size comparing Chepil’s analysis with wind—tunnel data of Reference BagnoldBagnold (1941), Reference ZinggZingg (1953), and Chepil (1945[b]).
While the situation depicted in Figure 3 would be quite unrealistic for sand or other particles without significant cohesion, it is probably a reasonable idealization for the most exposed grains on a snow surface, and is a simpler point of departure than the multiple—bond configuration. Overturning moments will be calculated around the point p, at the down—wind edge of the bond, where the bond radius x is smallest. The moments due to vertical forces acting through the particles center of gravity operate over moment arm x, the bond radius. Drag force F c again operates on a moment arm determined by the mean drag level so that
The weight of the particle W, and the cohesive bond F b, are opposed by lift L c.

Fig. 3. Diagram for analysis of forces on an exposed surface particle with a single cohesive bond.
Assuming Chepils' relation Lc = 0.85 Fc applies in this situation,
or

where the immersed weight of the particle is W = (4πR 3ρ’g/3). The bond strength is π X 2σ , where σ is the tensile strength at failure, so F b, = π X 2 σ at the initiation of particle motion. If ∆R denotes the distance above the center of the particle to the mean drag level, then tan Φ' = x/(R+∆R). Chepil’s integration of drag and velocity profile over the surface of a sphere at the level of the most exposed grains gives ∆R = 0.42R, so that tan Φ' = 0.7x/R. (Using the logarithmic velocity profile at this level is questionable, but necessary because experimental measurements in the region are lacking.)
When expressions for W, F b, and tan Φ' are substituted in Equation (11)

Consider Fc' as the drag per unit horizontal area occupied by the particle (F c' = F c/πR 2), and that this is larger than the drag per unit area of the surface by a factor that depends on the number of exposed grains in each unit area. Following Chepil’s notation, η is the ratio of drag per unit area of surface to drag per unit area of top grains (η = τ c/F c'), so that τ c, the surface shear stress at threshold, is

If this value obtains during a peak gust, then the ratio T = τ c /

This expression is for the very simple case of a single ice sphere bonded to a similar sphere on the surface by a neck of radius x with tensile strength σ.Reference Iversen, Iversen, Pollack, Greeley and WhiteIversen and others (1976), provide an analysis that includes interparticle forces for the situation depicted in Figure 1.
The point here is that for each size class of particles exposed on the surface there is an average critical force required for movement, and a corresponding distribution of critical forces around that mean value. The forces estimated by Equation (12) should not be considered as the mean value, because it seems likely that the analysis for the very exposed particle with a single bond would estimate forces below the mean value required for particles of that size. However, factors that effect cohesion and sintering (the change in x/R) should change the mean critical force in a way that is predictable from Equation (12). Evaluation of Equation (14) for ice spheres with several bond—to—radius ratios is shown (Fig.4) for η = 0.21, T = 2.5, ρ' = 0.9 Mg/m3, and σ = 10 bar. Threshold drag, calculated by Equation (14) shows negligible variation with particle diameter, even though the critical force of Equation (12) is strongly size dependent. This results from dividing the force by the projected particle area to obtain surface drag. The drag required to break even the smallest cohesive bonds is at least an order of magnitude larger than that required to overcome particle weight.
Reference HobbsHobbs (1974) summarized cohesion measurements for ice spheres. Experiments on the force required to separate an ice sphere from a plane ice surface (Reference Yamada and ŌuraYamada and Ōura, 1969) were noted by Kuroiwa ([1975]). The nature of the bond that produces cohesion between ice has been a scientific controversy, and remains in question. For a natural snow surface, impurities are quite likely within the precipitation crystals. It seems probable that rotations at the bond, as reported by Reference NakayaNakaya and Matsumoto (1954), would occur for the idealized surface particle of Figure 3, at least for temperatures above — 10°C. Equating the cohesive force to that required to exceed the tensile strength of an ice bond with radius x may over—simplify the problem.

Fig. 4. Mean drag required to remove ice spheres bonded to the surface by a single bond, computed from Equation (14) for several bond/radius ratios.
Measured cohesion definitely increases as a function of the size of ice sphere (Table 1). Experiments (Reference Hosier, Hosler, Jensen and GoldshlakHosler and others, 1957) determined the effect of temperature on cohesion quite well (Fig. 5), and data from Nakaya and Matsumoto can be compared by normalizing the forces by the force estimated from an exponential function fit to measurements for each sphere, for example at — 15°C. The curve F b = 8Fb(—15) exp (0.141 T), gives an empirical relation that describes the effect of temperature T in Celsius degrees on the cohesion of Table 1 14.6 mm diameter spheres in an environment saturated with respect to ice. Considering the procedure in these cohesion experiments, Figure 5 should be interpreted as the effect of temperature on cohesion measured within about one minute after contact between ice surfaces.
Table I. Measured cohesion of ice at —5°C

Nakaya and Matsumoto were impressed by the large increase in cohesion with small increases in initial contact pressure. According to Reference Hosier, Hosler, Jensen and GoldshlakHosier and others (1957), cohesion on contact between ice spheres is also a strong function of humidity. The initial contact area is apparently smaller at low humidities, and, for a completely dry atmosphere, the strength of the bond decreases to a negligible value above —5°C.

Fig. 5. Cohesion of ice spheres, measured soon after contact, decreases exponentially with decreasing temperature. Data are normalized by the cohesion at — 15 oC to allow comparison of several sphere diameters.
Kuroiwa ([1975]) presents fluidization measurements by Matsumaru, who estimated cohesion for powder snow at —7°C to be F b = 0.085 dyn (8.5 X 10—7 N). It appears that the normal force required to break the cohesive bond can vary over several orders of magnitude, from a low of the order 10—3 dyn (10—8 N), soon after contact between small particles at low temperatures, to a high of the order 103 dyn (10—2 N),for large particles sintered to x/R = 0.25. In sum, experiments on cohesion of ice show
(1) cohesion increases rapidly with particle size,
(2) strength of cohesion on contact decreases exponentially with decreasing temperature,
(3) the initial cohesive force is less at a given temperature the lower the humidity with respect to saturation over ice, and (4) initial contact pressure increases the initial cohesion, even when the pressure is immediately removed.
Excellent laboratory work (again summarized by Reference HobbsHobbs (1974)) related the bond growth of sintering ice spheres to time t and temperature T according to the relation

where B(T) is a function of temperature (see Appendix). The conclusion of these experiments (Reference Hobbs and MasonHobbs and Mason, 1964) is that bond growth occurs by condensation of water vapor transferred through the environment by diffusion. This transfer is apparently much more rapid in the natural snow—pack, presumably due to convection. Reference KeelerKeeler (1969) presents data from thin sections of natural dry snow showing that x/R increases from 0.02 for snow two days old to 0.25 by day 47 after precipitation. Beyond that, x/R changed little during the remainder of the snow—pack season.
For wind—speeds at the 10 m height ranging from 8 to 40 m/s, corresponding values of friction velocity are between 25 and 160 cm/s. Assuming air density is 1.0 kg/m3, the range of surface shear stress would be 0.625 to 11.2 dyn/cm2 (6.25 to 112 N/m2). According to Equation (14), in Figure 4 the aerodynamic drag at the 40 m/s wind—speed would not move surface particles bonded with x/R greater than 0.03, which is toward the low end of the expected bond—to—grain—size range. In other words, for snow surface particles where bonding has developed even slightly, the calculated critical force for particle motion is greater than drag on the particle produced in the normal range of the Earth’s atmospheric winds.
Impact forces on a surface particle
Once particles begin to move on a surface, or are injected into the airstream by some other means, an additional force is available to cause movement of surface particles. This section calculates the forces created by elastic impact of saltating particles.
Elastic properties of ice depend on the rate at which stress is applied. For particle collisions the stress rate is rapid and duration is short. In the range —3 to —40°C, Hooke’s law holds (Reference GoldGold, 1958) so that these collisions are expected to exhibit almost perfect elasticity. Although the elastic properties of ice crystals depend on crystal orientation, the blowing snow particles are assumed isotropic for these calculations. From the summary of values presented by Reference HobbsHobbs (1974), Young’s modulus E = 9.3 x 1o4 bar and Poisson’s ratio, v = 0.33 were chosen, and assumed independent of temperature.
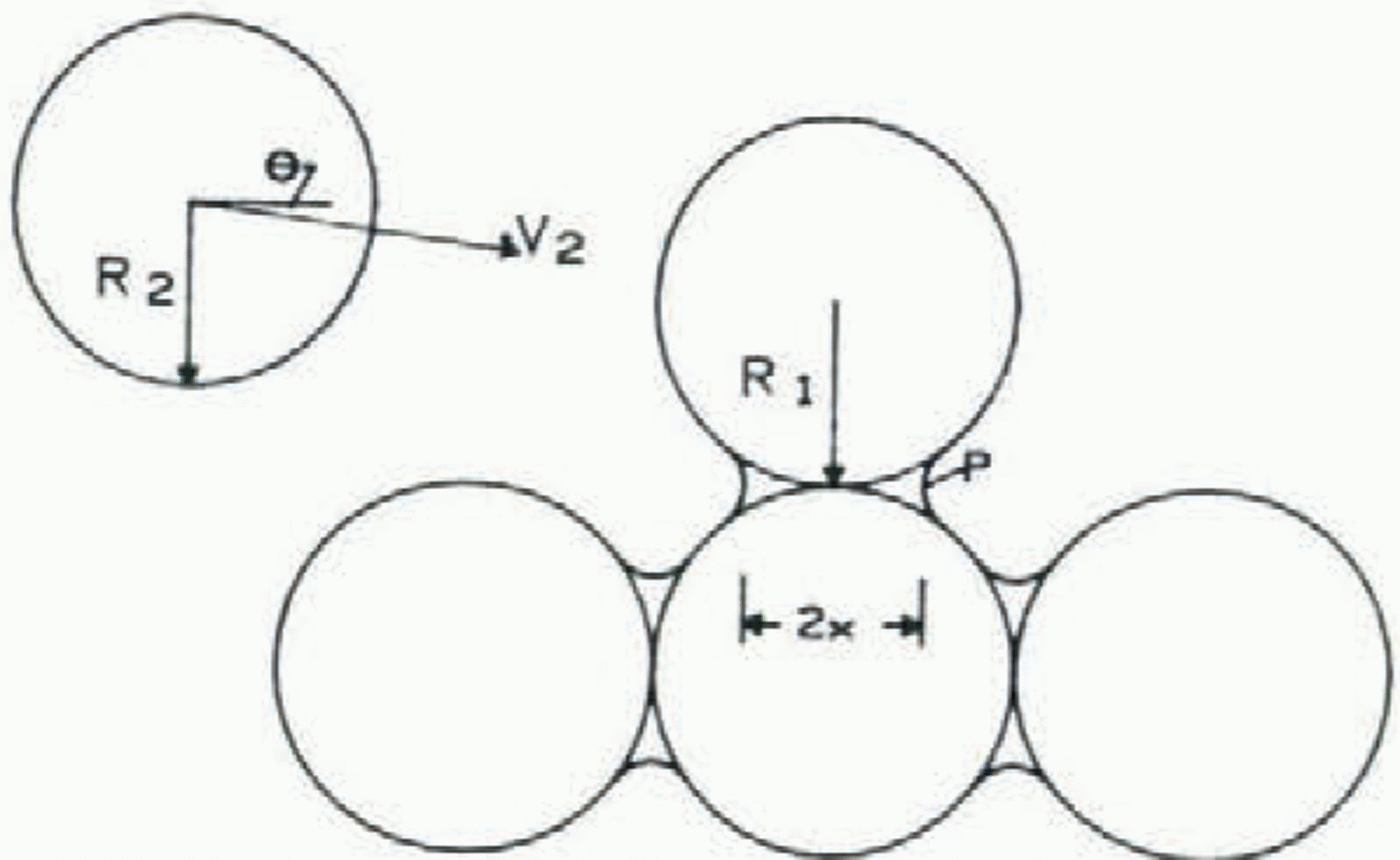
Fig. 6. Diagram for analysis of the force due to elastic collision on a surface particle with bond.
Using the classic analysis for collision of spheres first set forth by Hertz (see, for example, Reference NadeauNadeau, 1964), we will assume a sphere of radius R 1 at rest on the surface, being struck by a sphere of radius R 2, moving with velocity V 2 along a path declining by angle θ from the horizontal (Fig. 6). The collision is central, and α is the diminuation of distance between centers during impact. The sphere on the surface has mass m1 = 4πR 13ρ p/3 and for the moving particle, m 2 = 4πR 23ρ p/3.
During collision, deformation of both spheres occurs so that a circular area of contact forms, and the force F generated by the impact is equal to the integral of pressure over this contact area. The analysis gives the radius of this contact circle as

where k1 = (1— v 12) E 1 and k 2 = (1 —v 22)/E 2, E 1, E 2, v 1, and v 2 being Young’s modulus and Poisson's ratio respectively for the sphere denoted by the subscript. For the diminution α of distance between centers, the result is

The total energy of the impact is conserved, so that the sum of kinetic and potential energy must equal the total energy m2V2/2 where V is the velocity just before impact. The impact force is equal to the change in potential energy with a differential change in diminution. Maximum diminution αm occurs when all kinetic energy is converted to potential energy, and the analysis gives

where

Total time of contact, or the duration of the collision, is

To evaluate the maximum force that will be exerted on the surface particle by the collision, Equation (18) is evaluated to get αm, and Equation (17) provides the relation between αm and the maximum force, which occurs at α = αm. The elastic constants are assumed equal so k1 = k 2 = k, where k is 9.6 x 10—6 bar—1. Impact forces (Fig. 7) were computed for the central collision of a sphere with one of similar size at rest on the surface.
The impact force F e, in a central elastic collision, develops a clockwise moment (F e cos θ) (R sin θ) and a counter—clockwise moment (F e sin θ) (x+R cos θ) around point p. If we assume that net moment F e(R cos θ—x sin θ), is equal to the moment required to initiate particle motion (Fig. 1), then

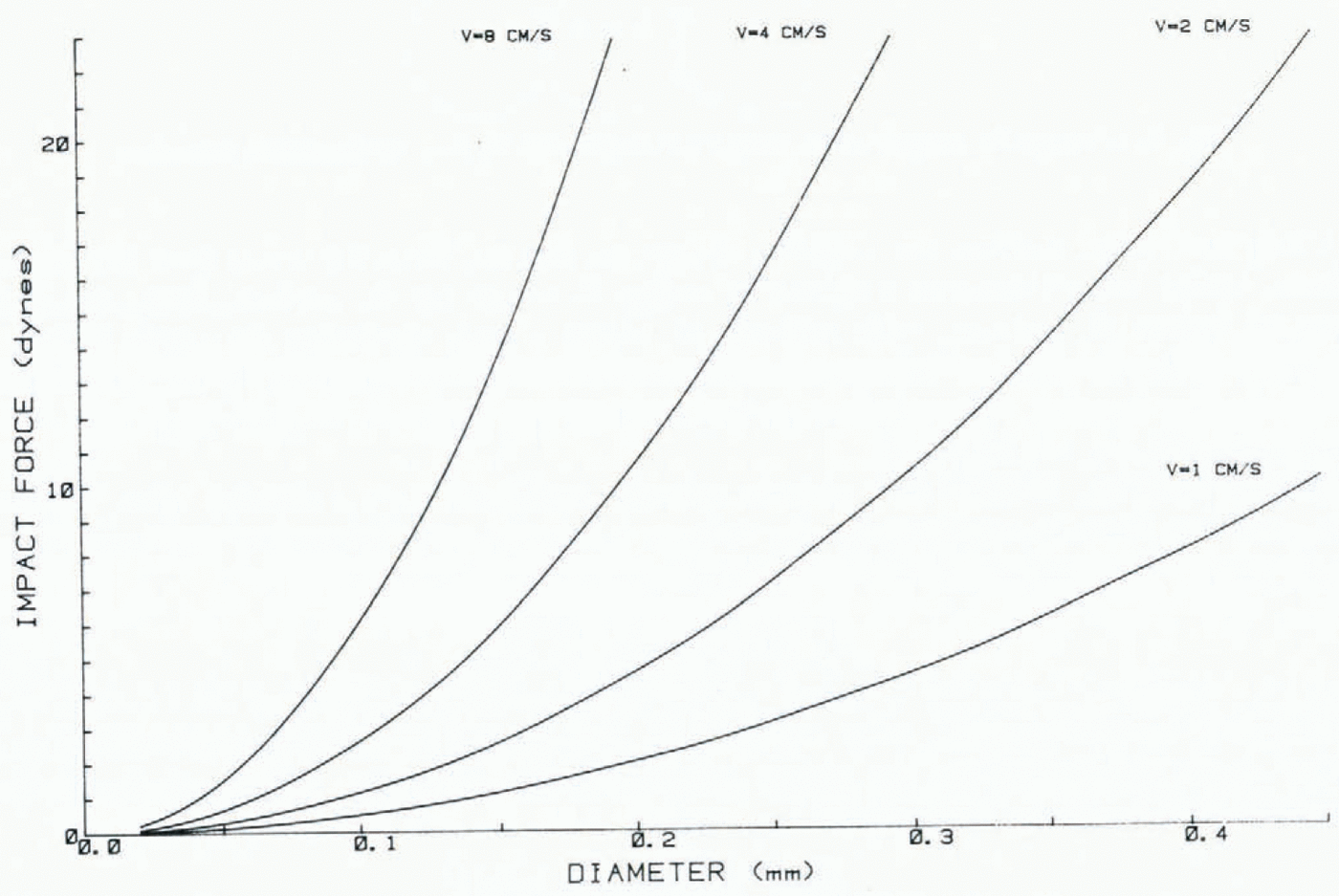
Fig. 7. Force created by central collision of an ice sphere with a similar sphere at rest.
Or

Evaluation of Equation (14) showed the force required to overcome the bond strength was much larger than W. Assuming lift Lc is also small compared to F b = πR 2(x/R) 2σ, the impact force of a saltating particle on a surface particle at the threshold of pardcle motion is approximated by

According to this, the impact force that will move a particle of radius R bonded to the surface by a single ice bond of radius x and tensile strength σ can be estimated. Such a force will Figure 8 produce some maximum compression αm that can be computed from Equation (17). Then, the velocity at impact can be calculated by Equation (18). Such a procedure was used to calculate impact velocities of uniform ice spheres, at the impact threshold (Fig. 8). The increase in impact force with particle size compensates for the increase in bond area at constant x/R, so that threshold impact velocity is independent of particle size for the approximation (23). The impact angle θ makes slight difference in estimated impact threshold velocity within the range 50 < θ < 15°.

Fig. 8. Threshold impact velocity of ice sphere required to move a sphere of similar size, bonded to the surface with a single ice bond of radius x. Impact angle is 10° below horizontal, and collision is central.
Discussion
To interpret the information on ice cohesion and elastic impact in terms of the wind—speed threshold for movement of a snow surface, it is necessary to recognize that a distribution of grain—sizes and bond strengths exists among the exposed surface particles, and that there is also a distribution of shear stress associated with the turbulent wind. Reference GesslerGessler (1970) has applied the concept that there is a certain probability that the shear stress of a given flow will exceed the critical stress required for movement of a given particle size, to predict the stabilization of alluvial channels by armoring with coarser grains of the sediment distribution. His argument can also be applied to the movement of snow particles by fluid forces, if it is recognized that the critical shear is determined by bond strength rather than by the particle Reynolds number. Snow exhibits amazing strength almost immediately after wind deposition, and this must certainly be a factor in the stability of drifts behind obstacles. Even a slight decrease in the frequency with which maximum gusts occur, results in a longer average rest between particle moves and thus a greater threshold for movement.
A probabilistic description of the phenomenon becomes even more interesting when we consider the impact threshold. Reference White and SchulzWhite and Schulz (1977), from high—speed motion pictures of the saltation trajectories of glass beads in a wind tunnel, showed that, in addition to the fluid drag, a lift force was required in the equations of particle motion to explain the observed trajectories. This lift was assumed to result from particle spin in the range from 100—300 rev/s for which their photographs offer some evidence (as do those of Chepil (1945[b]) for soil and Kobayashi (1972) for snow). Particle impact velocities are determined primarily by the longitudinal wind speed at the maximum height of saltation trajectory. These trajectory heights in turn, depend on particle size, the wind velocity profile in the saltation layer, and the lift—off velocity due to rebound from elastic collision.
Upon impact of a saltating snow particle with an exposed surface particle, a force develops in opposition to the bond or bonds holding the surface particle. If these bonds do not fracture, the potential energy of the elastic compression must overcome the cohesion at the contact between the surface and impacting particle, or the particle will stick and become part of the surface. Reference KobayashiKobayashi (1972) experimented with an ice sphere dropped on a thick ice plane to determine the coefficient of restitution. His results showed the strong effect of cohesion in reducing the height of rebound at warmer temperatures. These results seemed to explain the observations of ŌReference Ōura, Ōura, Ishida, Kobayashi, Kobayashi and Yamadaura and others (1967) that the threshold wind—speed for snow transport at Syowa Station, Antarctica, increased with increasing temperature above —7°C. More recent measurements of the restitution coefficient by Reference Araoka and MaenoAraoka and Maeno (1978) suggest, however, that plastic deformation, rather than cohesion, is the primary factor that reduces particle energy upon rebound. Assuming that the particle strikes with momentum such that it will rebound without breaking a bond, then its lift—off velocity will be some function of the impact velocity. From this, it is logical to expect that the height of saltation depends, in part, on the strength of surface bonds.
Average particle trajectories, calculated by White and Schulz, show an increase in expected height with particle size. Measured size distributions of blowing snow, although mostly for heights above the saltation layer (Reference Budd and RubinBudd and others, 1966) show a general decrease in size with height. It seems reasonable that the momentum of the larger particles is more likely to be sufficient to break surface bonds, and even if this does not occur, the larger size of the particles creates a greater cohesion on impact, which reduces the momentum of rebound, with the net result that large particles have average trajectories with lower heights than small particles.
Conclusions
The threshold wind—speed for transport of snow is determined primarily by the degree of cohesive bonding rather than particle size, in contrast to the single function found by Bagnold for sand and verified by others for materials with insignificant cohesion. From experiments on the cohesion of ice, the threshold wind speed for snow transport is expected to vary in the following ways.
(i) The initial threshold at the time of deposition will be higher at warmer temperatures, with higher humidity, and if deposition occurs with wind. Initial cohesion increases with temperature, humidity, and contact force.
(ii) Threshold wind speed will increase with time since deposition. The increase slows with time and is slower at colder temperatures. This assumes that the mechanism is similar to sintering of ice spheres, although more rapid, due probably to convection.
From calculations and experiments on the elastic impact of ice:
(iii) The threshold for wind transport of a snow surface will be much lower if there is a source of particles, such as precipitating snow, snow on trees, or surface hoar, that will create initial saltation, since the particle—impact forces are much higher than wind drag on surface grains or projections.
(iv) The distribution of saltation trajectory heights depends on the distribution of cohesive bonds for exposed particles. The greater the impact—threshold wind speed, the higher will be the particle trajectories, not only at the threshold but also at greater wind—speeds. The impact threshold will be influenced by cohesion between impacting particles and surface grains so that a given wind—speed will be less effective in eroding a surface at warmer temperatures and higher humidities.
If the calculated forces presented in this analysis are of the same order—of—magnitude as those actually occurring in natural snow transport, then cohesion is often stronger than forces on the surface particle due to wind drag. Computed particle velocities for impact threshold, on the other hand, are low compared to longitudinal wind velocities expected at maximum saltation trajectory heights. This suggests that saltation impacts in many cases produce forces sufficient to break more than one particle from the surface.
After reviewing the knowledge of how threshold wind—speed depends on the various factors that determine the cohesion of a snow surface, it should be apparent that (a) the threshold wind—speed of a snow surface determines the distribution of saltation trajectories of the transport and (b) those factors that determine the threshold wind—speed continue to govern the transport mechanism at winds in excess of the threshold. These facts make the threshold wind—speed a critical parameter of any general equation for mass transport of snow as a function of wind speed, and certainly one which must be properly scaled for realistic modeling.
Acknowledgements
This paper was improved by several suggestions offered by Dr J. L. Kovner, after his very careful review, for which I thank him. I also appreciated helpful comments by A. Judson.
Appendix
Evaluation of the temperature function for sintering rate of ice spheres
THE function B(T) derived by Reference Hobbs and MasonHobbs and Mason (1964) expresses the effect of temperature on the growth of bonds between ice spheres according to Equation (15). The mechanism is described as diffusion of water molecules in the vapor phase through the environment to the bond, where condensation occurs. A balance is required between the rate of condensation and the rate at which latent heat can be dissipated. This leads them to the equation

The variables are listed below, first those with a constant value, then those that are temperature dependent :
γ surface tension of ice 109 mJ m—2 (109 erg/cm2) (Reference HobbsHobbs, 1974, p. 346).
δ intermolecular spacing 2.76 Å (2.76x 10—8 cm) (Reference HobbsHobbs, 1974).
k Boltzmann constant 1.38 x 10—16 erg/K (1.38X 10—23J K—1).
ß ice density 0.92 Mg/m3.
m mass of water molecule 2.922 x 10—23 g (2.922 x 10—26 kg) (Reference HobbsHobbs, 1974).
Temperature—dependent variables are expressed in terms of absolute temperature T:
DG diffusion coefficient of water vapor in air (DG — 0.206 (T0/273K)1.75(P0)/P cm2/s where P 0 is standard atmospheric pressure and P is the pressure of the environment (Reference Thorpe and MasonThorpe and Mason, 1966)).
K thermal conductivity of air (K = [5.748 + 0.018 46(T—273 K)]10-5 cal/cms K = = [2.407+0.007 73 ( T-273)] 10-2 J/m s K (for the range 243 K ≤ T ≤ 273 K)(Reference LeeLee, 1975, p. 134)).
Ls latent heat of sublimation (Ls = 677 - 0.056 75(T-273 K)—0.000 751 6(T-273 K)2 cal/g = 2.834X 1o6 —237.6(T—273 K)— 3.147(T— 273 K)2J/kg (Reference LeeLee, 1975, from data in Reference ListList, 1949)).
po equilibrium vapor pressure (log P 0= -9.097 18(T0/T-1) —3.566 54 log10(T0/T) ++ 0.876 793(1 —T/T0) + log10 6.107 1; T 0 = 273.16 K (List, 1949, p. 350)).
The solution of B(T) is plotted (Fig. A1), for two atmospheric pressures, to show the decrease of the parameter with temperature and the relative effect of elevation.
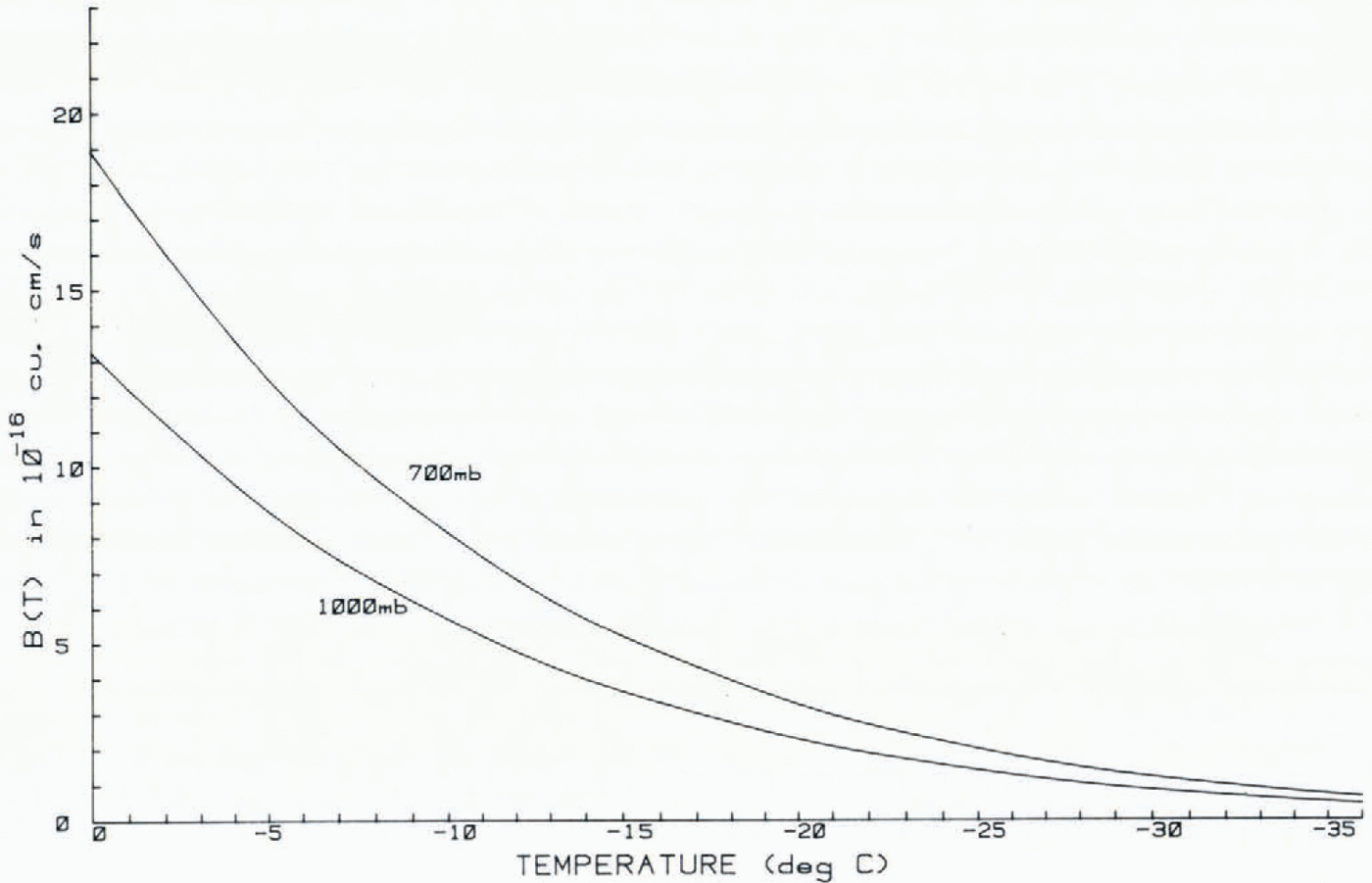
Fig. A1. Evaluation of the ice sintering temperature function derived by Reference HobbsHobbs and Mason (1969) for two atmospheric pressures.












