Introduction
Extensive snow covers are among the few natural surfaces where “hydraulically smooth” boundary-layer wind flows are frequent even in relatively exposed sites (Reference Bergen and SwansonBergen and Swanson, 1964). This type of boundary-layer flow is probably typical for snow covers under forest canopy where wind movement is greatly attenuated. Such flows differ from the more familiar “hydraulically rough” flow in that the actual surface elements are not exposed to turbulence; instead they are submerged in a layer of non-turbulent air in which the movement of momentum or other atmospheric properties, such as sensible heat or water vapor, is due to molecular diffusion alone, i.e. the “laminar sublayer”. This paper compares some field observations of wind speed and snow surface properties with relations predicted by Reference Beavers and JosephBeavers and Joseph (1967), who hypothesized that the rate of change of wind speed with height in the laminar sub-layer is inversely proportional to the square root of the specific permeability.
Nikuradse experimentally established (Reference SchlictingSchlicting, 1968) that the vertical profile of wind speed for “smooth” flows may be written in the same form as that for a “rough” flow for heights above the laminar sub-layer:
where U is the wind speed at a height Z above the surface, u⋆ is the “friction velocity” defined in terms of the air density ρ and the surface shear stress τ by
and ZL is a scaling height.
The factor ϕ (Lumley and Panofsky, [c1964]) varies with the ratio of the sensible heat flux to the surface to τ and vanishes when that ratio approaches zero, i.e. for “neutral” stabilities. For neutral stability the apparent level of zero velocity occurs at ZL while the friction velocity is equal to about 0.4 times the speed at a height of 2.303 ZL
In “rough flow”, ZL is a characteristic of the surface—the “roughness length”, but for “smooth” flow laboratory measurements over impermeable surfaces (Reference SchlictingSchlicting, 1968) indicate that
where v is the kinematic viscosity of the air. The same measurements establish a criterion for smooth flow in terms of the roughness length Z0 :
Since ZL for smooth flow must be larger than Z0 for the same surface, a smooth flow is assured if:
For “smooth” flow, Equation (1) contains only one free parameter, u⋆. The value of u⋆ obtained from Equation (3) and that estimated from the wind speed at 2.303 ZL should agree.
Equation (1) not only defines an effective drag coefficient for the surface, but is the basis for estimates of the local heat-transfer coefficient (Reference SchlictingSchlicting, 1968).
For “smooth” flow, Equation (1) is valid only above the laminar sub-layer, a height which experiments indicate is about 
. Below this height, turbulent mixing becomes negligible and the velocity profile is linear, with a slope specified by the condition that τ is constant with height:
For a solid wall, an additional condition is that
which is sometimes called the “non-slip condition”. For a permeable surface Equation (7) does not hold because a non-zero horizontal velocity U s may be present in the pores of the material, often called the “slip velocity”.
Under this condition, Equation (6) will require an adjustment to Equation (1) such that
Equation (8) implies that the local drag coefficients and heat-transfer coefficients will be a function of U s as well as U ⋆; and that the coefficients calculated on the basis of Equation (7) will be in error to the extent that U s is an appreciable fraction of U ⋆.
An estimate of U s in terms of U, measured at some practical reference level, and some reasonably accessible property of the snow surface thus becomes of particular interest in applied studies of snow-cover thermal regimes.
Reference Ruff and GelharRuff and Gelhar (1972) have investigated the more general problems of estimating slip velocities for any type of boundary-layer flow over a porous surface. They did not place any explicit restriction on the magnitude of the flow velocities induced in the porous material by the surface shear, i.e. the flow may be outside the Darcy range (Reference BenderBender, 1957), and the transfer of momentum between levels in the porous material may include that due to a velocity-dependent “apparent viscosity” representing the joint effects of turbulence and dispersion.
The results are relatively indefinite and involve at least one constant of the material, the “Forchheimer” or quadratic flow resistance constant, that is known to depend upon grain-size and geometry (Reference BenderBender, 1957) but which has never been explicitly determined for snow.
The problem of estimating U s becomes considerably simpler if we can assume that flow velocities in the medium are within the Darcy range, less than about 5 cm s-1 for fine grained snow (Reference BenderBender, 1957), and that the momentum transfer is due entirely to a constant fluid viscosity operating in the pore spaces. These two assumptions seem plausible for “smooth” flow, and lead to an expression first published by Reference Beavers and JosephBeavers and Joseph (1967) in a study of laminar flow in a flume with a porous floor. They were able to correlate the flume friction factor with the specific permeability k of the porous material by assuming that
where Q was the volume flow per unit area in the material corresponding to Darcy flow through the flume pressure gradient and to k, and where the velocity gradient is evaluated on the fluid side of the porous surface. The coefficient β is independent of viscosity and, apparently, a function of pore geometry and porosity. For two beds of packed granules of unspecified, but apparently differing, porosities β was about 10.
An elementary analysis with the assumption of laminar, Darcy flow indicates that β should be less than or equal to unity, as does the result of a physical simulation of flow over a porous medium (Reference TaylorTaylor, 1971).
Equation (6) implies vanishing horizontal pressure gradients in the boundary layer and hence that Q may be neglected in Equation (9). When Equation (6) is evaluated at the surface and used to eliminate the derivative in Equation (9), then
Measurements
The data used in this study were obtained during an experiment with a different objective than to test Equation (10). In this experiment surface air permeability and the vertical profile of wind speed were measured simultaneously. These data, although very limited, offered the first opportunity to assess the plausibility of Equation (10) for a snow surface.
The experimental site was a helicopter pad of 300 m diameter at about 3 000 m altitude and bounded by trees about 20 m tall.
Vertical profiles of wind speed were measured over the snow cover near the center of the clearing with a Thornthwaite sensitive-cup anemometer array. The array was mounted on a plywood base and equipped with a millimeter scale on the staff to record the local snow surface level. The cups were locaed tat 20, 40, 80, and 160 m above the base. Starting speed for the cups is about 10 cm s-1.
Density and air permeability of the top 19 cm of the snow surface were measured from samples taken from a trench located about midway between the wind-profile equipment and the forest edge. Samples were recorded in pairs by using standard SIPRE tubes inserted vertically into the snow surface. The trench was extended about 1 m between samplings.
Air permeability was measured by using the same equipment and procedures described earlier (Reference BergenBergen, 1968), except that the permeameter was calibrated between sample measurements with fiber-filled sample tubes.
The choice of the sample volume and depth was unfortunate from the viewpoint of a test of Equation (10). Sub-surface air flow would be concentrated in the top centimeter or so of the snow surface where porosities and air permeabilities could often be expected to exceed those typical of an average of the top 19 cm of the snow cover when the snow surface has settled.
At the beginning of the observations the snow surface was a thin, smooth melt crust. The anemometer array base was placed on the crust to be covered by subsequent snow-fall through the week. No surface ripple or drifting was evident until the last day.
About four, 15 min, wind-speed profiles were recorded each day. These data were plotted on log-linear graph paper with speeds assigned to the nominal anemometer heights less the snow surface height indicated by the scale on the staff.
Linearity of the plots was taken as evidence of neutral stability, i.e. the absence of profile curvature due to the last term in Equation (I). Profiles with only slight deviation were available for six days of observations. The parameter ZL was estimated by extrapolation to zero speed and u⋆ calculated from ZL and the plot as noted above. The profiles where u⋆ZL fell below the threshold of condition (5) were used for subsequent analysis.
The largest deviation from Equation (1) occurred with the wind-speed profile for the second day (11 March) and amounted to about 10% of the highest anemometer speed (Fig. 1). The anemometer output at the second highest level was unavailable on the fourth day due to a recorder malfunction.
Fig. 1. Vertical profiles of wind speed used for analysis.
The estimated ZL and U ⋆ values were used to calculate Us / U⋆ 2from the relation obtained by setting U equal to zero in Equation (8) and Z equal to zL with division by U⋆ :
The calculation of ZL from the various wind-speed profiles collected during the experiment suggests a maximum error of about 10% in the estimate of In zL and U *. The error in k with the same general procedure and equipment was about 20%.
The resulting estimates together with the measured values of 
are shown in Table I together with the porosity η of the surface sample.
The values of Us / U⋆2 and 
are plotted in Figure 2. The extreme deviation of the data for 8 March is probably due to the initial melt crust still lying within the layer of snow sampled by the tubes. This crust extending across the sample tube would result in erroneously low permeability estimates.
TABLE I. Estimates of wind-profile parameters and snow properties
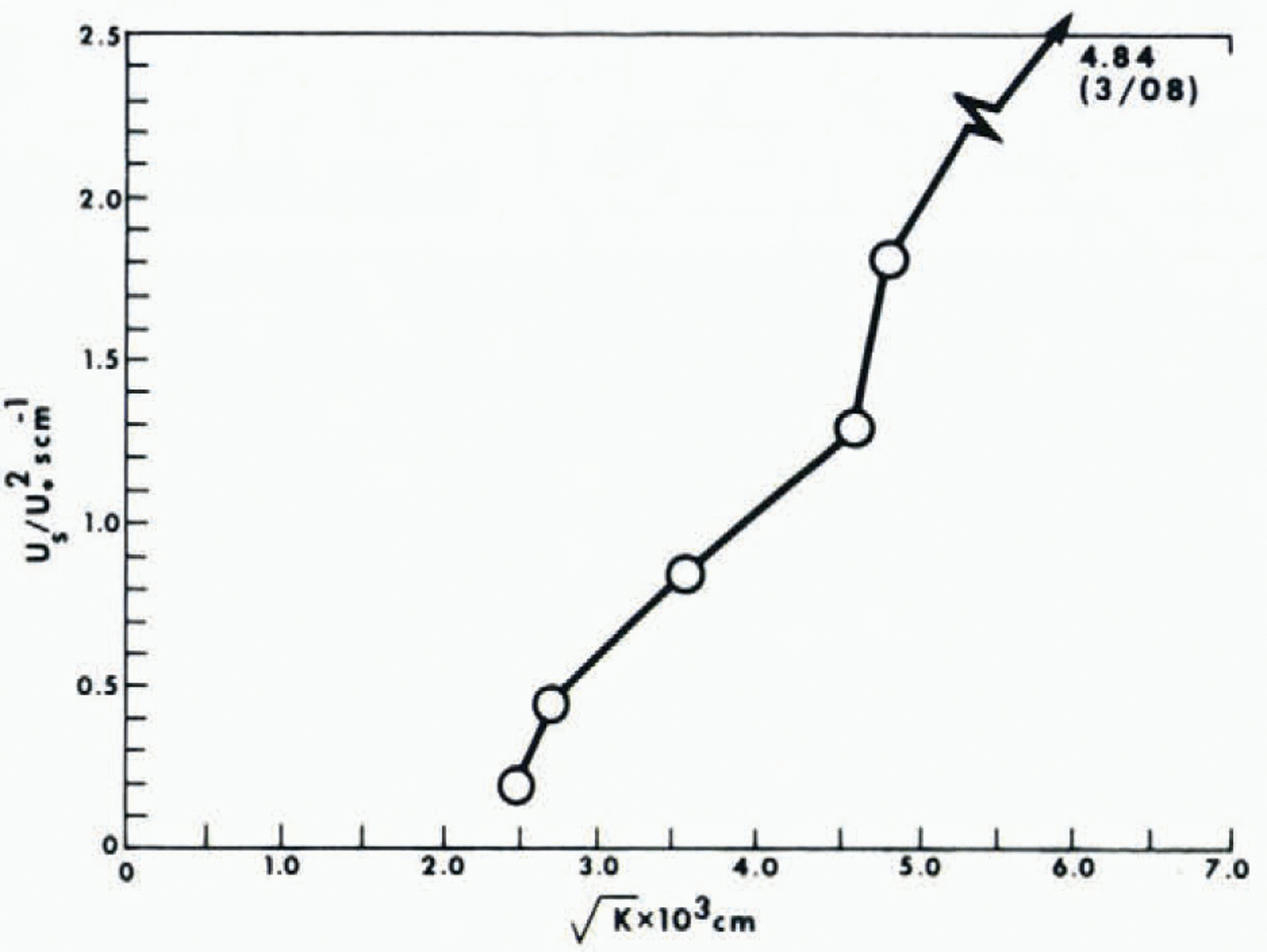
Fig. 2. Variation of the ratio of slip velocity to shear stress with the square root of the specific permeability.
While the data are too sparse for any rigorous test of Equation (8), the increase of U s / u⋆2 with 
is statistically significant at the 10% level if a normal distribution may be assumed for these variables. All the estimated U s / u⋆2 values are however an order of magnitude greater than those calculated from Equation (8) using a value of unity for β, and are larger than those computed with β = 10—the maximum reported by Beavers and Joseph. Perhaps significantly, the lowest value is found on the third day of the observations, just after the heaviest new-snow accumulation of the week. This condition suggests that k averaged over the 19 cm below the snow surface is considerably less than that relevant sub-surface flow. This difference would increase with snow settlement and metamorphosis. However, considering the variation of k with grain-size and porosity reported by Reference BenderBender (1957) and by others, it seems doubtful that the discrepancy in β due to this effect could amount to as much as an order of magnitude for the uncrusted snow layer.
An alternative explanation for the high values of β found in Reference Beavers and JosephBeavers and Joseph’s (1967) results and in this experiment is that the effective momentum transfer in snow is much less than that which would be predicted by using a kinematic viscosity formed by the product of the porosity and the kinematic viscosity of the fluid. Such a situation might arise if local, laminar separation of the flow within the porous medium was extensive.
Tests of the applicability of Equation (1) and eventually the more general results of Reference Ruff and GelharRuff and Gelhar (1972) will probably require measurements with a much finer resolution for k, e.g. for layers 1 cm thick. This is a task which will require modifications of the procedure and equipment heretofore used, but which should be well worthwhile because of the many implications of substantial sub-surface air flow in the surface snow layers.
