Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T13:56:05.791Z Has data issue: false hasContentIssue false
  • English
  • Français

Wake of super-hydrophobic falling spheres: influence of the air layer deformation

Published online by Cambridge University Press:  06 July 2018

Marco Castagna ,
Nicolas Mazellier Open the ORCID record for Nicolas Mazellier [Opens in a new window]  and
Azeddine Kourta
Marco Castagna
Affiliation:
University of Orléans, INSA-CVL, PRISME, EA 4229, 45072 Orléans, France
Nicolas Mazellier*
Affiliation:
University of Orléans, INSA-CVL, PRISME, EA 4229, 45072 Orléans, France
Azeddine Kourta
Affiliation:
University of Orléans, INSA-CVL, PRISME, EA 4229, 45072 Orléans, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report an experimental investigation of the wake of free falling super-hydrophobic spheres. The mutual interaction between the air layer (plastron) encapsulating the super-hydrophobic spheres and the flow is emphasised by studying the hydrodynamic performance. It is found that the air plastron adapts its shape to the flow-induced stresses which compete with the surface tension. This competition is characterised by introducing the Weber number 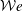${\mathcal{W}}e$, whilst the plastron deformation is estimated via the aspect ratio 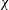$\unicode[STIX]{x1D712}$. While noticeable distortions are locally observed, the plastron becomes more and more spherical on average (i.e. 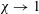$\unicode[STIX]{x1D712}\rightarrow 1$) as far as 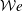${\mathcal{W}}e$ increases. The study of the falling motion reveals that the plastron compliance has a sizeable influence on the wake development. Investigating the lift force experienced by the super-hydrophobic spheres, the onset of wake instabilities is found to be triggered earlier than for smooth spheres used as reference. Surprisingly, it is also observed that the early promotion of the wake instabilities is even more pronounced beyond a critical Weber number, 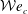${\mathcal{W}}e_{c}$, which corresponds to a critical aspect ratio 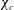$\unicode[STIX]{x1D712}_{c}$. Furthermore, the magnitude of the hydrodynamic loads is found to be dependent on the average deformation of the gas/liquid interface. Indeed, in comparison to the reference spheres, the high deformation achieved for 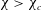$\unicode[STIX]{x1D712}>\unicode[STIX]{x1D712}_{c}$ (oblate shape) leads to lift and drag increase, whereas the low deformation obtained for 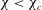$\unicode[STIX]{x1D712}<\unicode[STIX]{x1D712}_{c}$ (spherical shape) yields lift and drag mitigation. Accordingly, taking into account the plastron deformation provides an attractive way to explain the somehow discordant results reported in other studies at comparable Reynolds numbers. These results suggest that the amount of vorticity produced at the body surface and then released in the wake is strongly impacted by the plastron compliance. If confirmed by additional studies and extrapolated to other flow configurations, our findings would imply that plastron compliance and its feedback on the flow, which are currently neglected in most theoretical works and numerical simulations, must be accounted for to design super-hydrophobic surfaces and/or predict their performance.

JFM classification

Multiphase and Particle-laden Flows: Multiphase flow Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 850 , 10 September 2018 , pp. 646 - 673
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achenbach, E. 1972 Experiments on the flow past spheres at very high Reynolds numbers. J. Fluid Mech. 54, 565–575.Google Scholar
Achenbach, E. 1974 The effects of surface roughness and tunnel blockage on the flow past spheres. J. Fluid Mech. 65, 113–125.Google Scholar
Ahmmed, K. M. T., Patience, C. & Kietzig, A.-M. 2016 Internal and external flow over laser-textured superhydrophobic polytetrafluoroethylene (PTFE). ACS Appl. Mater. Interfaces 8, 27411–27419.Google Scholar
Alamé, K. & Mahesh, K.2018 Wall-bounded flow over a realistically rough superhydrophobic surface. J. Fluid Mech. (submitted). arXiv:1802.06845.Google Scholar
Aljallis, E., Sarshar, M. A., Datla, R., Sikka, V., Jones, A. & Choi, C.-H. 2013 Experimental study of skin friction drag reduction on superhydrophobic flat plates in high Reynolds number boundary layer flow. Phys. Fluids 25, 025103.Google Scholar
Auguste, F. & Magnaudet, J. 2018 Path oscillations and enhanced drag of light rising spheres. J. Fluid Mech. 841, 228–266.Google Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bhushan, B. & Jung, Y. C. 2011 Natural and biomimetic artificial surfaces for superhydrophobicity, self-cleaning, low adhesion, and drag reduction. Prog. Mater. Sci. 56, 1–108.Google Scholar
Byun, D., Kim, J., Ko, H. S. & Park, H. C. 2008 Direct measurement of slip flows in superhydrophobic microchannels with transverse grooves. Phys. Fluids 20, 113601.Google Scholar
Cassie, A. B. D. & Baxter, S. 1944 Wettability of porous surfaces. Trans. Faraday Soc. 40, 546–551.Google Scholar
Cheng, N.-S. 2009 Comparison of formulas for drag coefficient and settling velocity of spherical particles. Powder Technol. 189, 395–398.Google Scholar
Ellingsen, K. & Risso, F. 2001 On the rise of an ellipsoidal bubble in water: oscillatory paths and liquid-induced velocity. J. Fluid Mech. 440, 235–268.Google Scholar
Epps, B. P., Truscott, T. T. & Techet, A. H. 2010 Evaluating derivatives of experimental data using smoothing splines. In Proceedings of Mathematical Methods in Engineering International Symposium. MMEI, Coimbra, Portugal, pp. 29–38.Google Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Annu. Rev. Fluid Mech. 44, 97–121.Google Scholar
Fernandes, P. C., Risso, F., Ern, P. & Magnaudet, J. 2007 Oscillatory motion and wake instability of freely rising axisymmetric bodies. J. Fluid Mech. 573, 479–502.Google Scholar
Gruncell, B. R. K., Sandham, N. D. & McHale, G. 2013 Simulations of laminar flow past a superhydrophobic sphere with drag reduction and separation delay. Phys. Fluids 25, 043601.Google Scholar
Horowitz, M. & Williamson, C. H. K. 2010a The effect of Reynolds number on the dynamics and wakes of freely rising and falling spheres. J. Fluid Mech. 651, 251–294.Google Scholar
Horowitz, M. & Williamson, C. H. K. 2010b Vortex-induced vibration of a rising and falling cylinder. J. Fluid Mech. 662, 352–383.Google Scholar
Howe, M. S. 1995 On the force and moment on a body in an incompressible fluid, with application to rigid bodies and bubbles at high and low Reynolds numbers. Q. J. Mech. Appl. Maths 48, 401–426.Google Scholar
Jenny, M., Dušek, J. & Bouchet, G. 2004 Instabilities and transition of a sphere falling or ascending freely in a Newtonian fluid. J. Fluid Mech. 508, 201–239.Google Scholar
Jetly, A., Vakarelski, I. U. & Thoroddsen, S. T. 2018 Drag crisis moderation by thin air layers sustained on superhydrophobic spheres falling in water. Soft Matt. 14, 1608–1613.Google Scholar
Jung, T., Choi, H. & Kim, J. 2016 Effects of the air layer of an idealized superhydrophobic surface on the slip length and skin-friction drag. J. Fluid Mech. 790, R1.Google Scholar
Kim, N., Kim, H. & Park, H. 2015 An experimental study on the effects of rough hydrophobic surfaces on the flow around a circular cylinder. Phys. Fluids 27, 085113.Google Scholar
Kim, J. H. & Rothstein, J. P. 2017 Role of interface shape on the laminar flow through an array of superhydrophobic pillars. Microfluid. Nanofluid. 21:78. https://doi.org/10.1007/s10404-017-1914-7.Google Scholar
Lapple, C. E. & Sheperd, C. B. 1940 Calculation of particle trajectories. Ind. Engng Chem. 32, 605–617.Google Scholar
Lau, K. K. S., Bico, J., Teo, K. B. K., Chhowalla, M., Amaratunga, G. A. J., Milne, W. I., McKinley, G. H. & Gleason, K. K. 2003 Superhydrophobic carbon nanotube forests. Nano Lett. 3 (12), 1701–1705.Google Scholar
Lauga, E. & Stone, H. A. 2003 Effective slip in pressure-driven Stokes flow. J. Fluid Mech. 489, 55–77.Google Scholar
Leal, L. G. 1989 Vorticity transport and wake structure for bluff bodies at finite Reynolds number. Phys. Fluids 1, 124–131.Google Scholar
Legendre, D., Lauga, E. & Magnaudet, J. 2009 Influence of slip on the dynamics of two-dimensional wakes. J. Fluid Mech. 633, 437–447.Google Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32, 659–708.Google Scholar
Magnaudet, J. & Mougin, G. 2007 Wake instability of a fixed spheroidal bubble. J. Fluid Mech. 572, 311–337.Google Scholar
Martell, M. B., Blair Perot, J. & Rothstein, J. P. 2009 Direct numerical simulations of turbulent flows over superhydrophobic surfaces. J. Fluid Mech. 620, 31–41.Google Scholar
McHale, G., Shirtcliffe, N. J., Evans, C. R. & Newton, M. I. 2009 Terminal velocity and drag reduction measurements on superhydrophobic spheres. Appl. Phys. Lett. 94, 064104.Google Scholar
Min, T. & Kim, J. 2004 Effects of hydrophobic surface on skin-friction drag. Phys. Fluids 16, 55–58.Google Scholar
Mordant, N. & Pinton, J.-F. 2000 Velocity measurement of a settling sphere. Eur. Phys. J. B 18, 343–352.Google Scholar
Mougin, G. & Magnaudet, J. 2002a The generalized Kirchhoff equations and their application to the interaction between a rigid body and an arbitrary time-dependent viscous flow. Intl J. Multiphase Flow 28, 1837–1851.Google Scholar
Mougin, G. & Magnaudet, J. 2002b Path instability of a rising bubble. Phys. Rev. Lett. 88 (1), 014502.Google Scholar
Nilsson, M. A., Daniello, R. J. & Rothstein, J. P. 2010 A novel and inexpensive technique for creating superhydrophobic surfaces using Teflon and sandpaper. J. Phys. D: Appl. Phys. 43, 1–5.Google Scholar
Piao, L. & Park, H. 2015 Two-dimensional analysis of air-water interface on superhydrophobic grooves under fluctuating water pressure. Langmuir 31, 8022–8032.Google Scholar
Quéré, D. 2008 Wetting and roughness. Annu. Rev. Mater. Res. 38, 71–99.Google Scholar
Reinsch, C. H. 1967 Smoothing by spline functions. Numer. Math. 10, 177–183.Google Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 42, 89–109.Google Scholar
Samaha, M. A., Tafreshi, H. V. & Gad-el-Hak, M. 2012 Superhydrophobic surfaces: from the lotus leaf to the submarine. C. R. Meć. 340, 18–34.Google Scholar
Seo, J., García-Mayoral, R. & Mani, A. 2015 Pressure fluctuations and interfacial robustness in turbulent flows over superhydrophobic surfaces. J. Fluid Mech. 783, 448–473.Google Scholar
Shew, W. L., Poncet, S. & Pinton, J.-F. 2006 Force measurements on rising bubbles. J. Fluid Mech. 569, 51–60.Google Scholar
Shirtcliffe, N. J., McHale, G., Atherton, S. & Newton, M. I. 2010 An introduction to superhydrophobicity. Adv. Colloid Interface Sci. 161, 124–138.Google Scholar
Truscott, T. T., Epps, B. P. & Munns, R. H. 2016 Water exit dynamics of buoyant spheres. Phys. Rev. Fluids 1, 074501.Google Scholar
UltraTech International, Inc.2017 Webpage. http://www.spillcontainment.com/products/ever-dry, Accessed: December 2017.Google Scholar
Vakarelski, I. U., Chan, D. Y. C. & Thoroddsen, S. T. 2014 Leidenfrost vapour layer moderation of the drag crisis and trajectories of superhydrophobic and hydropholic spheres falling in water. Soft Matt. 10, 5662–5668.Google Scholar
Vakarelski, I. U., Marston, J. O., Chan, D. Y. C. & Thoroddsen, S. T. 2011 Drag reduction by Leidenfrost vapor layers. Phys. Rev. Lett. 106, 214501.Google Scholar
Vakarelski, I. U., Patankar, N. A., Marston, J. O., Chan, D. Y. C. & Thoroddsen, S. T. 2012 Stabilization of Leidenfrost vapour layer by textured superhydrophobic surfaces. Nature 489, 274–277.Google Scholar
Wu, J.-Z., Lu, X.-Y. & Zhuang, L.-X. 2007 Integral force acting on a body due to local flow structures. J. Fluid Mech. 576, 265–286.Google Scholar
Ybert, C., Barentin, C., Cottin-Bizonne, C., Joseph, P. & Bocquet, L. 2007 Achieving large slip with superhydrophobic surfaces: scaling laws for generic geometries. Phys. Fluids 19, 123601.Google Scholar
Zhang, X., Shi, F., Niu, J., Jiang, Y. & Wang, Z. 2008 Superhydrophobic surfaces: from structural control to functional application. J. Mater. Chem. 18, 621–633.Google Scholar
Zhang, Y.-L., Xia, H., Kim, E. & Sun, H.-B. 2012 Recent developments in superhydrophobic surfaces with unique structural and functional properties. Soft Matt. 8, 11217–11231.Google Scholar

Castagna et al. supplementay movie

Typical movie recorded (recording speed 1300 fps, reproduction speed 5 fps) in high magnification configuration for the SH-80 sphere (d = 20 mm). The gravity direction is from right to left.

Download Castagna et al. supplementay movie(Video)
Video 8.4 MB