Article contents
Vortex-induced vibrations of a sphere close to a free surface
Published online by Cambridge University Press: 11 May 2018
Abstract
Results are presented from an experimental investigation into the effects of proximity to a free surface on vortex-induced vibration (VIV) experienced by fully and semi-submerged spheres that are free to oscillate in the cross-flow direction. The VIV response is studied over a wide range of reduced velocities:
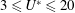 $3\leqslant U^{\ast }\leqslant 20$
, covering the mode I, mode II and mode III resonant response branches and corresponding to the Reynolds number range of
$3\leqslant U^{\ast }\leqslant 20$
, covering the mode I, mode II and mode III resonant response branches and corresponding to the Reynolds number range of
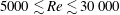 $5000\lesssim Re\lesssim 30\,000$
. The normalised immersion depth of the sphere is varied in small increments over the range
$5000\lesssim Re\lesssim 30\,000$
. The normalised immersion depth of the sphere is varied in small increments over the range
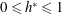 $0\leqslant h^{\ast }\leqslant 1$
for the fully submerged case and
$0\leqslant h^{\ast }\leqslant 1$
for the fully submerged case and
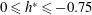 $0\leqslant h^{\ast }\leqslant -0.75$
for the semi-submerged case. It is found that for a fully submerged sphere, the vibration amplitude decreases monotonically and gradually as the immersion ratio is decreased progressively, with a greater influence on the mode II and III parts of the response curve. The synchronisation regime becomes narrower as
$0\leqslant h^{\ast }\leqslant -0.75$
for the semi-submerged case. It is found that for a fully submerged sphere, the vibration amplitude decreases monotonically and gradually as the immersion ratio is decreased progressively, with a greater influence on the mode II and III parts of the response curve. The synchronisation regime becomes narrower as
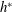 $h^{\ast }$
is decreased, with the peak saturation amplitude occurring at progressively lower reduced velocities. The peak response amplitude decreases almost linearly over the range of
$h^{\ast }$
is decreased, with the peak saturation amplitude occurring at progressively lower reduced velocities. The peak response amplitude decreases almost linearly over the range of
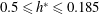 $0.5\leqslant h^{\ast }\leqslant 0.185$
, beyond which the peak response starts increasing almost linearly. The trends in the total phase,
$0.5\leqslant h^{\ast }\leqslant 0.185$
, beyond which the peak response starts increasing almost linearly. The trends in the total phase,
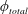 $\unicode[STIX]{x1D719}_{total}$
, and the vortex phase,
$\unicode[STIX]{x1D719}_{total}$
, and the vortex phase,
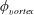 $\unicode[STIX]{x1D719}_{vortex}$
, reveal that the mode II response occurs for progressively lower
$\unicode[STIX]{x1D719}_{vortex}$
, reveal that the mode II response occurs for progressively lower
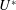 $U^{\ast }$
values with decreasing
$U^{\ast }$
values with decreasing
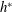 $h^{\ast }$
. On the other hand, when the sphere pierces the free surface, there are two regimes with different characteristic responses. In regime
$h^{\ast }$
. On the other hand, when the sphere pierces the free surface, there are two regimes with different characteristic responses. In regime
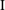 $\text{I}$
(
$\text{I}$
(
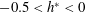 $-0.5<h^{\ast }<0$
), the synchronisation region widens and the vibration amplitude increases, surprisingly becoming even higher than for the fully submerged case in some cases, as
$-0.5<h^{\ast }<0$
), the synchronisation region widens and the vibration amplitude increases, surprisingly becoming even higher than for the fully submerged case in some cases, as
 $h^{\ast }$
decreases. However, in regime
$h^{\ast }$
decreases. However, in regime
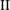 $\text{II}$
(
$\text{II}$
(
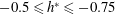 $-0.5\leqslant h^{\ast }\leqslant -0.75$
), the vibration amplitude decreases with a decrease in
$-0.5\leqslant h^{\ast }\leqslant -0.75$
), the vibration amplitude decreases with a decrease in
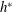 $h^{\ast }$
, showing a very sharp reduction beyond
$h^{\ast }$
, showing a very sharp reduction beyond
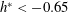 $h^{\ast }<-0.65$
. The response in regime II is characterised by two distinct peaks in the amplitude response curve. Careful analysis of the force data and phase information reveals that the two peaks correspond to modes I and II seen for the fully submerged vibration response. This two-peak behaviour is different to the classic VIV response of a sphere under one degree of freedom (1-DOF). The response was found to be insensitive to the Froude number (
$h^{\ast }<-0.65$
. The response in regime II is characterised by two distinct peaks in the amplitude response curve. Careful analysis of the force data and phase information reveals that the two peaks correspond to modes I and II seen for the fully submerged vibration response. This two-peak behaviour is different to the classic VIV response of a sphere under one degree of freedom (1-DOF). The response was found to be insensitive to the Froude number (
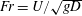 $Fr=U/\sqrt{gD}$
, where
$Fr=U/\sqrt{gD}$
, where
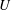 $U$
is the free-stream velocity,
$U$
is the free-stream velocity,
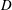 $D$
is the sphere diameter and
$D$
is the sphere diameter and
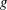 $g$
is the acceleration due to gravity) in the current range of
$g$
is the acceleration due to gravity) in the current range of
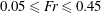 $0.05\leqslant Fr\leqslant 0.45$
, although higher Froude numbers resulted in slightly lower peak response amplitudes. The wake measurements in the cross-plane
$0.05\leqslant Fr\leqslant 0.45$
, although higher Froude numbers resulted in slightly lower peak response amplitudes. The wake measurements in the cross-plane
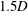 $1.5D$
downstream of the rear of the sphere reveal a reduction in the vorticity of the upper vortex of the trailing vortex pair, presumably through diffusion of vorticity into the free surface. For the piercing sphere case, the near-surface vorticity completely diffuses into the free surface, with only the opposite-signed vortex visible in the cross-plane at this downstream position. Interestingly, this correlates with an even higher oscillation amplitude than the fully submerged case. Finally, the effects of immersion ratio and diameter ratio (
$1.5D$
downstream of the rear of the sphere reveal a reduction in the vorticity of the upper vortex of the trailing vortex pair, presumably through diffusion of vorticity into the free surface. For the piercing sphere case, the near-surface vorticity completely diffuses into the free surface, with only the opposite-signed vortex visible in the cross-plane at this downstream position. Interestingly, this correlates with an even higher oscillation amplitude than the fully submerged case. Finally, the effects of immersion ratio and diameter ratio (
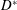 $D^{\ast }$
$D^{\ast }$
 $=$
sphere diameter/support-rod diameter) are quantified, showing care needs to be taken with these factors to avoid unduly influencing VIV predictions.
$=$
sphere diameter/support-rod diameter) are quantified, showing care needs to be taken with these factors to avoid unduly influencing VIV predictions.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 27
- Cited by



