Published online by Cambridge University Press: 05 January 2017
The dynamics of vortical structures in flow over a circular cylinder in the vicinity of a flat plate is investigated using particle image velocimetry (PIV). The cylinder is placed above the flat plate with its axis parallel to the wall and normal to the flow direction. The Reynolds number  $Re_{D}$ based on the cylinder diameter
$Re_{D}$ based on the cylinder diameter 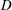 $D$ is 1072 and the gap
$D$ is 1072 and the gap 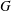 $G$ between the cylinder and the flat plate is varied from gap-to-diameter ratio
$G$ between the cylinder and the flat plate is varied from gap-to-diameter ratio 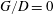 $G/D=0$ to
$G/D=0$ to 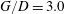 $G/D=3.0$. The flow statistics and vortex dynamics are strongly dependent on the gap ratio
$G/D=3.0$. The flow statistics and vortex dynamics are strongly dependent on the gap ratio 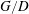 $G/D$. Statistics show that as the cylinder comes close to the wall (
$G/D$. Statistics show that as the cylinder comes close to the wall (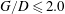 $G/D\leqslant 2.0$), the cylinder wake becomes more and more asymmetric and a boundary layer separation is induced on the flat plate downstream of the cylinder. The wake vortex shedding frequency increases with decreasing
$G/D\leqslant 2.0$), the cylinder wake becomes more and more asymmetric and a boundary layer separation is induced on the flat plate downstream of the cylinder. The wake vortex shedding frequency increases with decreasing 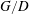 $G/D$ until a critical gap ratio (about
$G/D$ until a critical gap ratio (about 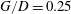 $G/D=0.25$) below which the vortex shedding is irregular. The deflection of the gap flow away from the wall and its following interaction with the upper shear layer may be the cause of the higher shedding frequency. The vortex dynamics is investigated based on the phase-averaged flow field and virtual dye visualization in the instantaneous PIV velocity field. It is revealed that when the cylinder is close to the wall (
$G/D=0.25$) below which the vortex shedding is irregular. The deflection of the gap flow away from the wall and its following interaction with the upper shear layer may be the cause of the higher shedding frequency. The vortex dynamics is investigated based on the phase-averaged flow field and virtual dye visualization in the instantaneous PIV velocity field. It is revealed that when the cylinder is close to the wall (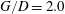 $G/D=2.0$), the cylinder wake vortices can periodically induce secondary spanwise vortices near the wall. As the cylinder approaches the wall (
$G/D=2.0$), the cylinder wake vortices can periodically induce secondary spanwise vortices near the wall. As the cylinder approaches the wall (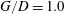 $G/D=1.0$) the secondary vortex can directly interact with the lower wake vortex, and a further approaching of the cylinder (
$G/D=1.0$) the secondary vortex can directly interact with the lower wake vortex, and a further approaching of the cylinder (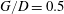 $G/D=0.5$) can result in more complex interactions among the secondary vortex, the lower wake vortex and the upper wake vortex. The breakdown of vortices into filamentary debris during vortex interactions is clearly revealed by the coloured virtual dye visualizations. For
$G/D=0.5$) can result in more complex interactions among the secondary vortex, the lower wake vortex and the upper wake vortex. The breakdown of vortices into filamentary debris during vortex interactions is clearly revealed by the coloured virtual dye visualizations. For 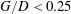 $G/D<0.25$, the lower shear layer is strongly inhibited and only the upper shear layer can shed vortices. Investigation of the vortex formation, evolution and interaction in the flow promotes the understanding of the flow physics for different gap ratios.
$G/D<0.25$, the lower shear layer is strongly inhibited and only the upper shear layer can shed vortices. Investigation of the vortex formation, evolution and interaction in the flow promotes the understanding of the flow physics for different gap ratios.
Movie 4 for Figure 13: Instantaneous vortical structures at G/D=0.5 revealed by virtual dye visualization.