Published online by Cambridge University Press: 09 July 2013
Numerical results from large-scale, long-time, simulations of decaying homogeneous turbulence are reported, which indicate that blow-up of inviscid flows is tamed by the emergence of collective dynamics of coherent structures. The simulations also suggest that this collective dynamics might lead to universal behaviour during the transient evolution of turbulence. In particular, simulations with three different initial conditions show evidence of a 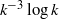 ${k}^{- 3} \log k$ spectrum in the transient stage, before the Kolmogorov
${k}^{- 3} \log k$ spectrum in the transient stage, before the Kolmogorov 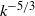 ${k}^{- 5/ 3} $ asymptotic regime is attained. Such a universal transient might serve as a spectral funnel to the time-asymptotic Kolmogorov spectrum, which is invariably observed in the late stage of all three simulations presented in this work. The present work is entirely based on simulation evidence. However, the statistical analysis of the coherent structures suggests an analogy with population dynamics, which might be conducive to new mathematical models of transient decaying turbulence.
${k}^{- 5/ 3} $ asymptotic regime is attained. Such a universal transient might serve as a spectral funnel to the time-asymptotic Kolmogorov spectrum, which is invariably observed in the late stage of all three simulations presented in this work. The present work is entirely based on simulation evidence. However, the statistical analysis of the coherent structures suggests an analogy with population dynamics, which might be conducive to new mathematical models of transient decaying turbulence.
This movie refers to the KP initial condition at Re = 5000, with a spatial resolution of 10243, using a PS code. It shows three plots of maximum vorticity versus time, energy spectra and Taylor microscale Reynolds number versus time, respectively. The k-3 log k scaling (middle plot) in energy spectrum, in relation with the attainment of the first maxima in maximum vorticity at t ~ 2.1, is well apparent in the movie. The spectra quickly aligns with the k-3 log k line when the first maxima in maximum vorticity is reached, and then moves towards the k^-5/3 scaling, when the magnitude of maximum vorticity decreases and the flow enters a constant decay stage. The movie runs from t = 0 - 10.
Like the previous one, this movie shows the simulation result of TG initial condition at Re = 5000 and N = 10243, from t = 0-12, using a PS code. Unlike the KP flow, the first maximum in maximum vorticity is attained at t~4, where the k-3log k scaling is observed. From the movie, it is also evident that the global maxima in maximum vorticity is reached long after the first local maximum. The flow then goes towards the steady decay, where k-5/3 scaling in energy spectra is observed.
This movie refers to the simulation of a group of six Hills vortices, one from centre of each side, colliding at the centre of the periodic box. This initial condition is different from the previous ones, as it shows no symmetry. Notwithstanding this lack of symmetry, the movie confirms the existence of k-3 log k scaling, in accordance with the first maxima of maximum vorticity. It should also be noted that PS methods with periodic boundary conditions cannot represent exactly the jump in vorticity across the boundary of the vortex. This implies a small violation of incompressibility which shows however no appreciable effect on the spectral dynamics of the flow.
Indication from tracking of maximum vorticity that vorticity saturation is driven by collision-like events among high vorticity blob (0.9 of maximum vorticity at a given time, shown in movie in yellow color) and low vorticity blobs (0.5 of maximum vorticity at a given time, shown in movie in green color).