Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zheng, Qinmin
and
Alam, Md. Mahbub
2019.
Evolution of the wake of three inline square prisms.
Physical Review Fluids,
Vol. 4,
Issue. 10,
Jiang, Hongyi
and
Cheng, Liang
2020.
Flow separation around a square cylinder at low to moderate Reynolds numbers.
Physics of Fluids,
Vol. 32,
Issue. 4,
Brandao, Filipe L.
Bhatt, Mrugank
and
Mahesh, Krishnan
2020.
Numerical study of cavitation regimes in flow over a circular cylinder.
Journal of Fluid Mechanics,
Vol. 885,
Issue. ,
Chen, Weilin
Ji, Chunning
Xu, Dong
Zhang, Zhimeng
and
Wei, Yuhan
2020.
Flow-induced vibrations of an equilateral triangular prism at various angles of attack.
Journal of Fluids and Structures,
Vol. 97,
Issue. ,
p.
103099.
Chen, Weilin
Ji, Chunning
Xu, Dong
and
Zhang, Zhimeng
2020.
Vortex-induced vibrations of two inline circular cylinders in proximity to a stationary wall.
Journal of Fluids and Structures,
Vol. 94,
Issue. ,
p.
102958.
Zhu, Jianxun
Holmedal, Lars Erik
Myrhaug, Dag
and
Wang, Hong
2020.
Near-wall effect on flow around an elliptic cylinder translating above a plane wall.
Physics of Fluids,
Vol. 32,
Issue. 9,
Zhu, Hongjun
Tang, Tao
Zhou, Tongming
Liu, Hongye
and
Zhong, Jiawen
2020.
Flow structures around trapezoidal cylinders and their hydrodynamic characteristics: Effects of the base length ratio and attack angle.
Physics of Fluids,
Vol. 32,
Issue. 10,
Zhu, Hongjun
and
Liu, Wenli
2021.
Wake structure and evolution of flow over a finned circular cylinder.
Physics of Fluids,
Vol. 33,
Issue. 7,
Shui, Qingxiang
Duan, Cuie
Wang, Daguo
and
Gu, Zhaolin
2021.
New insights into numerical simulations of flow around two tandem square cylinders.
AIP Advances,
Vol. 11,
Issue. 4,
Jiang, Hongyi
2021.
Formation mechanism of a secondary vortex street in a cylinder wake.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Shan, Xiangjun
2021.
Effect of an upstream cylinder on the wake dynamics of two tandem cylinders with different diameters at low Reynolds numbers.
Physics of Fluids,
Vol. 33,
Issue. 8,
Zhu, Hongjun
Chu, Xin
Yan, Zhiyin
and
Gao, Yun
2021.
Coupling response of flow-induced oscillating cylinder with a pair of flow-induced rotating impellers.
Physics of Fluids,
Vol. 33,
Issue. 8,
Zhu, Hongjun
Tang, Tao
Gao, Yun
Zhou, Tongming
and
Wang, Junlei
2021.
Flow-induced vibration of a trapezoidal cylinder placed at typical flow orientations.
Journal of Fluids and Structures,
Vol. 103,
Issue. ,
p.
103291.
Li, Han
Huang, Qiaogao
Pan, Guang
and
Dong, Xinguo
2021.
Wake instabilities of a pre-swirl stator pump-jet propulsor.
Physics of Fluids,
Vol. 33,
Issue. 8,
Dynnikova, G. Ya.
Dynnikov, Ya. A.
Guvernyuk, S. V.
and
Malakhova, T. V.
2021.
Stability of a reverse Karman vortex street.
Physics of Fluids,
Vol. 33,
Issue. 2,
Zhu, Hongjun
Zhong, Jiawen
and
Zhou, Tongming
2021.
Wake structure characteristics of three tandem circular cylinders at a low Reynolds number of 160.
Physics of Fluids,
Vol. 33,
Issue. 4,
Jiang, Hongyi
2021.
Three-dimensional wake transition of a diamond-shaped cylinder.
Journal of Fluid Mechanics,
Vol. 918,
Issue. ,
Wang, Duo
Liu, Yang
Li, Heng
and
Xu, Hongyi
2021.
Secondary instability of channel-confined transition around dual-circular cylinders in tandem.
International Journal of Mechanical Sciences,
Vol. 208,
Issue. ,
p.
106692.
Kim, Ildoo
2021.
On the morphology of two-dimensional laminar vortex streets behind triangles.
Physics of Fluids,
Vol. 33,
Issue. 3,
Kumar, Pankaj
and
Kalita, Jiten C.
2021.
A comprehensive study of secondary and tertiary vortex phenomena of flow past a circular cylinder: A Cartesian grid approach.
Physics of Fluids,
Vol. 33,
Issue. 5,
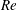 $Re$) between 200 and 300, and (ii) the pairing of two opposite-sign vortices, followed by the merging of the paired vortices into subsequent vortices, over a range of
$Re$) between 200 and 300, and (ii) the pairing of two opposite-sign vortices, followed by the merging of the paired vortices into subsequent vortices, over a range of 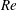 $Re$ between 400 and 1000. Single vortices may be generated between the merging cycles due to mismatch of the vortices. The irregular merging process results in flow irregularity and an additional frequency signal
$Re$ between 400 and 1000. Single vortices may be generated between the merging cycles due to mismatch of the vortices. The irregular merging process results in flow irregularity and an additional frequency signal 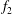 $f_{2}$ (in addition to the primary vortex shedding frequency
$f_{2}$ (in addition to the primary vortex shedding frequency 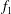 $f_{1}$) in the two-layered and secondary vortex streets. In particular, a gradual energy transfer from
$f_{1}$) in the two-layered and secondary vortex streets. In particular, a gradual energy transfer from 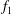 $f_{1}$ to
$f_{1}$ to 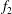 $f_{2}$ with distance downstream is observed in the two-layered vortex street prior to the merging. The frequency spectra of
$f_{2}$ with distance downstream is observed in the two-layered vortex street prior to the merging. The frequency spectra of 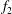 $f_{2}$ are broad-band for
$f_{2}$ are broad-band for 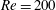 $Re=200$–300 but become increasingly sharp-peaked with increasing
$Re=200$–300 but become increasingly sharp-peaked with increasing 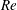 $Re$ because the vortex merging process becomes increasingly regular. The ratio of the sharp-peaked frequencies
$Re$ because the vortex merging process becomes increasingly regular. The ratio of the sharp-peaked frequencies 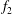 $f_{2}$ and
$f_{2}$ and 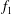 $f_{1}$ is equal to the ratio of the numbers of vortices observed after and before the merging. The general conclusions drawn from a circular cylinder are expected to be applicable to other bluff bodies.
$f_{1}$ is equal to the ratio of the numbers of vortices observed after and before the merging. The general conclusions drawn from a circular cylinder are expected to be applicable to other bluff bodies.

