3.1. Mean flow

The mean flow is presented with contours of $u$-velocity normalised by the freestream speed of sound in figure 2. Important flow features can be observed including a long recirculation bubble that extends over the suction side, from the detachment at $x = 0.34$ until its reattachment at $x = 0.82$. In the magnified view, a small bubble can be observed on the pressure side, followed by a recirculation region at the trailing edge. The blue contours enclosed by magenta lines indicate regions of reversed flow.

Figure 2. Contours of mean streamwise velocity $\bar {u}$ normalised by freestream speed of sound. The magenta dashed lines depict the reversed flow boundaries which include a wide separation bubble on the suction side besides a small bubble on the pressure side, near the trailing edge.

Distributions of root-mean-square (RMS) for kinetic energy $k$ and pressure $p$ are presented in figures 3(a) and 3(b), respectively. As it can be seen from the plots, fluctuations start amplifying along the bubble and the highest values appear at the reattachment region, on the suction side. The green and blue dashed lines in figures 3(a) and 3(b), respectively, depict the locations of maximum $k$ and $p$ along the shear layer forming on the suction side. In the following analyses, these lines will be used as reference locations for data extraction to track flow disturbances. Again, the solid magenta line shows the recirculation bubble.

Figure 3. RMS values of (a) kinetic energy and (b) pressure. The green and blue dashed lines depict locations of maximum fluctuations along the shear layer on the suction side, whereas the magenta solid line delimits the reversed flow region.

The negative mean pressure coefficient $-C_p$ is shown in figure 4(a) with blue and red solid lines for suction and pressure sides, respectively. To highlight the regions with intense fluctuations, the pressure coefficient is presented as $-C_p \mp C_{p_{{RMS}}}$, where the blue dashed and red dotted lines correspond to the suction and pressure sides, respectively. The peak value of pressure coefficient on the suction side is observed near the leading edge at $x = 0.02$. From this point onward, a pressure increase leads to a drop in $-C_p$ until reaching a plateau along the LSB. The plateau extends up to $x = 0.7$, where the pressure further increases towards the trailing edge, causing another drop in $-C_p$. Pressure fluctuations are shown in figure 4(d) for both suction and pressure sides. The RMS values of $C_p$ are low along the entire pressure side, and upstream of the bubble ($x \lesssim 0.5$) on the suction side. However, they increase towards the peak at $x \approx 0.78$ on the suction side.

Figure 4. Mean and RMS distributions of (a,d) pressure and (b,e) friction coefficients along the airfoil surface, and (c, f) tangential velocity profiles computed in the wall-normal direction $\Delta n$.

The mean skin friction $C_f$ distribution over the airfoil is presented in figure 4(b). The RMS values of skin friction $C_{f_{{RMS}}}$, shown in figure 4(e), are also added to the mean values. A magnified view highlights the presence of the LSB which starts at $x = 0.34$ and reattaches at $x = 0.67$. The reattachment is followed by a second detachment which reaches a minimum at $x = 0.75$ and reattaches at $x = 0.82$. The nature of the double detachment profile is discussed in details by Duck et al. (Reference Duck, Ruban, Theofilis, Hein and Dallmann2000). The RMS peaks at $x \approx 0.76$ due to the high value of $k$ shown in figure 3(a).

Mean tangential velocity profiles extracted along the wall-normal direction $\Delta n$ are presented in figure 4(c) at different locations along the chord. At the detachment point, $x = 0.34$, the red curve indicates the zero wall-normal derivative in the velocity profile. At $x = 0.73$, the velocity profile shown as a grey line exhibits the maximum reversed flow of $-0.13 U_\infty$. The orange line shows a velocity profile at $x = 0.95$, where 3-D effects are important due to turbulent transition. In figure 4( f), RMS values of the tangential velocity are presented and a single peak is observed for the profile computed at $x = 0.34$. Velocity fluctuations increase inside the bubble at $x = 0.64$ and become dominant at $x = 0.73$. In both these locations, the velocity fluctuations present triple peak profiles as also observed by Nash et al. (Reference Nash, Lowson and McAlpine1999), Desquesnes et al. (Reference Desquesnes, Terracol and Sagaut2007) and Duck et al. (Reference Duck, Ruban, Theofilis, Hein and Dallmann2000). Near the trailing edge at $x = 0.95$, where a turbulent regime may occur, mixing results in a smoother velocity fluctuation profile.

3.2. Vortex dynamics

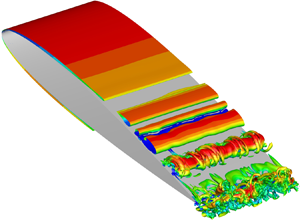
Instantaneous 3-D flow fields over the airfoil are presented in figure 5 with iso-surfaces of Q-criterion coloured by $u$-velocity. A magenta shade along the airfoil surface depicts the region of reversed flow along the separation bubble. This figure shows 2-D rolls that are visible along the separation bubble and amplify on the suction side, leading to vortex shedding. Moreover, different flow regimes are observed at the trailing edge, where coherent structures alternate with periods of turbulent packets. For example, figure 5(a) shows a single laminar-like roll reaching the trailing edge at $t = 20.82$ whereas figure 5(b) shows that, at $t = 21.78$, vortex breakdown leads to a turbulent regime near the trailing edge. Readers are referred to the movie of the flow field provided as supplementary movie 1 are available at https://doi.org/10.1017/jfm.2022.129 for detailed inspection of the present flow dynamics.

Figure 5. Instantaneous iso-surfaces of Q-criterion coloured by $u$-velocity show regimes with (a) coherent structures at the trailing edge (high spanwise coherence, $t=20.82$) and (b) smaller-scale turbulent eddies (low spanwise coherence, $t=21.78$).

The analysis of flow snapshots is important to understand the vortex dynamics over the airfoil suction side. Based on the acoustic analogy of Ffowcs-Williams & Hall (Reference Ffowcs-Williams and Hall1970), efficient sound generation is achieved when pressure fluctuations are aligned with an edge, such that it will be maximum for 2-D-like perturbations. In this sense, figure 6 shows the spanwise-averaged $\omega _z$ vorticity, where blue and red contours represent negative and positive values, respectively. A dark blue colour indicates strong spanwise coherence of a 2-D vortex, whereas light blue contours are representative of uncorrelated turbulence. A thin black line is used to identify individual vorticity packets, based on the iso-contour of an entropy measure given by ${p}/{\rho ^{\gamma }} - ({p_{\infty }}/{\rho _{\infty }^{\gamma }}) = 0.1\,\%$. This separates the region where vorticity is important from where the flow is irrotational, outside the boundary layer. A magenta dashed line represents the border of averaged negative $\bar {u}$ velocity, as discussed in figure 2. The simulation time is shown in convective time units on the lower left corner of all plots. A movie of figure 6 is provided as supplementary movie 2 to aid the dynamic visualisation of the flow features.

Figure 6. Spanwise-averaged vorticity $\omega _z$ shows vortex pairing over the airfoil. The magenta dashed line represents the boundary of reversed flow (negative $\bar {u}$). The black lines connecting the sub-figures mark the evolution of vortices with high ($\boldsymbol {-}$ and ${-}\,{-}$) or low ($\cdots$ and ${-}\cdot {-}$) spanwise coherence.

As shown in figure 6, the flow dynamics is dominated by events on the suction side, where vortices are shed from the LSB. During the shedding process, there is a possibility that the 2-D laminar vortices undergo a process of vortex pairing. In case this process is not successful, vortex bursting leads to turbulent transition and low coherence along the span, represented by dotted lines. These turbulent packets may interact with other vortices and further reduce their coherence, as indicated by the dashed-dotted line. On the other hand, if the vortices merge or only a solitary vortex is shed from the bubble, the trend is for either structure to keep its high coherence up to the trailing edge. Both of these processes are represented by the dashed (merging) and solid (single vortex) lines in figure 6. A detailed discussion on the consequence and cause of this behaviour is presented in §§ 3.3 and 3.6, respectively. Similar dynamics of vortex shedding from LSBs are observed experimentally by Kurelek et al. (Reference Kurelek, Lambert and Yarusevych2016).

As shown in the experimental investigations of Pröbsting & Yarusevych (Reference Pröbsting and Yarusevych2015) and Pröbsting et al. (Reference Pröbsting, Scarano and Morris2015), for this Reynolds number and angle of attack, it is expected that the pressure side does not play an important role in terms of the flow dynamics. In order to confirm this observation, a temporal signal of pressure fluctuation is extracted at $x = 0.98$, marked by the blue dashed line in figure 3(b). A second signal is obtained for the velocity derivative in the wall-normal direction on the pressure side at $x = 0.95$. Both signals are presented in figure 7(a) as well as the time-averaged ${\rm d} \bar {u}/{\rm d} n$, indicating that the flow is, on average, recirculating (${\rm d} \bar {u}/{\rm d} n<0$). In the velocity derivatives, the wall-normal direction is positive pointing outwards from the airfoil surface. Snapshots of the flow dynamics are presented in 7(b), where the red–blue contours are the $\omega _z$ vorticity, similarly to the previous figures, the green hatched colours show instantaneous regions of negative $u$-velocity whereas the dashed magenta line indicates the boundaries of the time-averaged pressure side bubble. In this figure, it is possible to see that when a vortex arrive at the trailing edge from the suction side at $t = 20.59$ (negative $p'$ peak), the flow reattaches on the bottom side (positive ${\rm d} u/{\rm d} n$ at the wall). As the vortex leaves the airfoil surface on the suction side at $t=20.73$, the pressure increases on the suction side (positive $p'$) and, as a consequence, the flow detaches on the pressure side (negative ${\rm d} u/{\rm d} n$). Thus, the magenta dashed line in figure 7(a) shows that the recirculation bubble exists on an time-averaged sense. Moreover, these figures show that the pressure side dynamics seems to be a reaction to the suction side events in the present flow.

Figure 7. Intermittency of the pressure side bubble exhibits dependence on the suction side vortices as presented for (a) temporal signals and (b) flow snapshots. In (a), the pressure signal is extracted on the suction side at $x = 0.98$ and the velocity derivative is computed on the pressure side at $x = 0.95$. In (b), the hatched green region indicates instantaneous values of negative $u$-velocity. In both plots, the magenta dashed line indicates negative values in the time-averaged $u$-velocity.

3.3. Intermittency and sound generation

The acoustic analogy of Ffowcs-Williams & Hall (Reference Ffowcs-Williams and Hall1970) states that efficient acoustic scattering occurs due to flow fluctuations near a trailing edge. In this sense, the hydrodynamic near field with pressure fluctuations is presented in figures 8(a) and 8(c) with black–white contours, while the acoustic field is presented in figures 8(b) and 8(d). In the latter, the levels are presented 10 times lower compared with the former. The figures also display $\omega _z$ vorticity in red–blue colours. To highlight the spanwise coherence, regions of $|\omega _z| > 24$ are plotted as filled contours. The vortex cores are related to lower pressures (white background contours) whereas the gaps between the cores display higher pressures (black contours). A coherent vortex at the trailing edge is presented in figure 8(a) at a time instant $t=20.82$. The highly coherent hydrodynamic structure leads to efficient acoustic scattering at the trailing edge which, in turn, induces the emission of an intense acoustic wave. The wave is scattered with a ${\rm \pi}$ phase opposition relative to the incident fluctuations and it reaches the leading edge at a retarded time $t = 21.31$, as shown in figure 8(b). When the flow is turbulent, at $t = 21.78$, a less-coherent vorticity packet reaches the trailing edge as shown in figure 8(c). In this case, a weaker acoustic wave is emitted from the trailing edge, reaching the leading edge at a retarded time of $t = 22.27$, as exhibited in figure 8(d). A movie of figure 8 is submitted as supplementary movie 3 to show the relation between the acoustic field and vortex dynamics.

Figure 8. Acoustic radiation from the airfoil. (a) A coherent structure near the trailing edge at $t = 20.82$ and (b) its subsequent intense acoustic wave reaching the leading edge, at a retarded time $t = 21.31$. (c) An uncorrelated turbulent packet near the trailing edge at $t = 21.78$ and (d) its subsequent weaker acoustic wave reaching the leading edge, at a retarded time $t = 22.27$. Note that the levels from (b) and (d) are 10 times lower than those from figures (a) and (c).

Temporal signals are acquired at different positions along the blue dashed line in figure 3(b) in terms of spanwise-averaged non-dimensional pressure. The signal at the trailing edge is presented in figure 9(a) and displays intermittent deep valleys related to the passage of coherent structures as shown in figure 8(a). The signal also shows low-amplitude oscillations related to the turbulent packets that carry a negative pressure envelope, as described in figure 8(b). Such behaviour can be characterised as an amplitude modulation of the signal. The same trends are also observed in the acoustic pressure signal, which is extracted one chord above the trailing edge, at $(x,y) = (1c,1c)$, and presented in figure 9(c). It is possible to see that the low-pressure valleys from figure 9(a) result in high-pressure peaks that reach the observer position at a retarded time.

Figure 9. Time-signal and Fourier transform of spanwise-averaged pressure at different locations (a) and (b) inside the boundary layer along the chord and (c) and (d) in the acoustic field.

The magnitude of the Fourier coefficients is presented in figure 9(b) and 9(d) for the hydrodynamic and acoustic fields, respectively, displaying equidistant multiple tones. The Fourier transforms employ a frequency domain averaging with an overlap of $67\,\%$ amongst 4 bins covering the entire period. The frequency resolution is $\Delta f = 0.03$ and a Hanning window function with energy correction is applied. All tonal peaks are integer multiples of the lowest-frequency tone, $St \approx 0.5$. As it can be seen in figure 9(b), the dominant peak at the trailing edge is at $St \approx 3.5$ for probes located close to the leading edge ($x = 0.05$), at the detachment point ($x = 0.34$) and the trailing edge ($x = 0.98$). This frequency is related to the passage of low-pressure packets, either turbulent or coherent. At $x = 0.64$, in the shear-layer roll-up region, the dominant peak moves to higher frequencies which may be related to the smaller-scale instabilities yet to be merged into larger vortices. In the acoustic field, figure 9(d) presents results extracted at one and five chords above the trailing edge. The same frequencies are observed where $St = 3.5$ is still the most prominent peak.

As can be seen from figure 9(a), coherent structures often reach the trailing edge with a slow timescale of $\Delta t \approx 2.0$ convective time units, which corresponds to a frequency $St = 0.5$. However, due to the chaotic motion, this process is not perfectly periodic and multiple vortices may reach the trailing edge within this period, as indicated by the time differences $\Delta t = 0.22$, 0.25, 0.29, 0.33 and 0.40 in the figure. In this faster time scales, the different intervals are related to frequencies $St = 4.5$, 4.0, 3.5, 3.0 and 2.5, respectively, which are integer multiples of the low-frequency tone at $St = 0.5$.

To better highlight this behaviour, a time-frequency analysis is also performed with the continuous wavelet transform (CWT) using the complex Morlet wavelet (Farge Reference Farge1992), as shown in figure 10. The present wavelet function is the product of a monochromatic complex exponential with a Gaussian envelope. Its spectral response is an exponentially decaying band-pass filter centred around the frequency of the complex exponential. The filter width depends on the Gaussian standard deviation. The scalogram presents how the correlation of the wavelet with a reference signal changes in time based on the wavelet frequency. Hence, higher values indicate strong fluctuations of the signal at a particular frequency and time. Results are obtained for the same probe locations considered in figure 9(b). The scalograms from figures 10(a) and 10(c) exhibit longer periods of intense pressure fluctuations at $St = 3.5$, whereas in figure 10(b), a broader range of frequencies is excited more intensely. As it can be seen from the probe at $x=0.64$, frequencies higher than $St = 3.5$ are excited, particularly $St = 4.5$, $5.0$ and $5.5$. One should note that the colour levels are different for each location, with lower and higher amplitudes for probes at $x=0.34$ and $0.98$, respectively. These figures show that the secondary tones present intermittent behaviour, with each frequency experiencing periods of silence (blue contours) and loud noise emission (green, yellow and red contours). Another important aspect captured by the scalograms is the amplitude modulation of the signals. Such behaviour has an important role in the generation of secondary tones, as discussed by Desquesnes et al. (Reference Desquesnes, Terracol and Sagaut2007), Pröbsting et al. (Reference Pröbsting, Serpieri and Scarano2014) and Ricciardi et al. (Reference Ricciardi, Arias-Ramirez and Wolf2020).

Figure 10. Time-frequency analysis of pressure fluctuations using a CWT at (a) the detachment point $x = 0.34$, (b) shear-layer roll-up $x = 0.64$ and (c) trailing edge $x = 0.98$.

3.4. Linear analysis and amplification mechanisms

In order to investigate the growth of velocity and pressure fluctuations at the tonal frequencies, figure 11 presents Fourier transforms of the temporal signals extracted along the airfoil suction side, following the green (velocities) and blue (pressure) dashed lines from figures 3(a) and 3(b), respectively. In this analysis, the temporal signals are computed for the spanwise-averaged normal and tangential velocity components $u_n$ and $u_t$, respectively, in addition to pressure $p$. Results are plotted together with the RMS values (solid black line) extracted from figure 3. Both $\hat {u}_t$ and $\hat {p}$ show strong amplification downstream of $x = 0.5$, which coincides with the location of the recirculation bubble. Furthermore, a plateau is observed upstream of $x = 0.5$ for pressure fluctuations, which indicates that acoustic waves dominate over hydrodynamic disturbances along this region. Pressure fluctuations at $St \approx 3.5$ exhibit higher amplitudes along the entire chord and similar observations can be made for the velocity components. As discussed by Kurelek et al. (Reference Kurelek, Yarusevych and Kotsonis2019), it is possible that these fluctuations act as a sub-harmonic forcing that stimulates the vortex merging process.

Figure 11. Magnitude of Fourier transform coefficients for (a) normal velocity $\hat {u}_n (St,x)$, (b) tangential velocity $\hat {u}_t (St,x)$ and (c) pressure $\hat {p} (St,x)$ computed along the green (velocities) and blue (pressure) lines from figures 3(a) and 3(b), respectively. Each colour represents a tonal frequency, identified in the colourbar, whereas the RMS is presented as the black line.

The mechanisms of generation and amplification of flow instabilities is explained by linear stability theory. In this regard, bi-global linear stability and resolvent analyses are employed to understand the most sensitive frequencies in terms of optimal forcing and response characteristics for 2-D perturbations, i.e. only for spanwise wavenumber $\beta = 0$. This is justified because 2-D structures are expected to radiate noise more efficiently (Sano et al. Reference Sano, Abreu, Cavalieri and Wolf2019). In the LNS operator, the off-diagonal terms, related to velocity gradients and shear, lead to a non-normal operator. Hence, orthogonality of the stability modes is not expected and interaction among modes within the system may lead to transient response that affect its short-term dynamics (Schmid Reference Schmid2007). This behaviour is properly captured by the resolvent analysis, which provides the information on eigenvalue sensitivity and transient energy amplification rate.

Following the theoretical and numerical methodology described in § 2.2, the eigenvalue spectrum from a bi-global stability analysis is presented in figure 12. The black circles represent the physically meaningful eigenvalues whereas the empty grey symbols are spurious eigenvalues. The latter could be identified due to their large displacement in the complex plane during the grid/sponge convergence study (not shown) as well as by visualisation of the associated eigenvectors (modes). Sensitivity of the operator to external disturbances is computed by the resolvent analysis along both real (frequency) and imaginary (growth rate) axes and it is measured by the pseudospectrum, presented as the contour plot in figure 12. The region of analysis in the resolvent operator is limited by means of matrices $\boldsymbol{\mathsf{B}}$ and $\boldsymbol{\mathsf{C}}$ in (2.10). Only the near-field grid points are considered, i.e. those inside the dashed red rectangle in figure 1. This is physically justified because the most intense quadrupole noise sources which are responsible for the incident field in the acoustic scattering process are close to the trailing edge (Wolf et al. Reference Wolf, Azevedo and Lele2012a). As an additional positive side effect, this improved results by reducing spatial support of spurious eigenvectors.

Figure 12. Spectrum (symbols) and pseudospectrum (contours in logarithmic scale) of the linearised compressible Navier–Stokes equations for 2-D spanwise perturbations $(\beta = 0)$. Higher frequencies present larger sensitivity as shown in light blue and green colours.

Results from the bi-global stability analysis in terms of the eigenspectrum are presented in figure 12. It is possible to see multiple eigenvalues at frequencies close to those from the LES, previously discussed in figure 9(b,d). For instance, the maximum relative deviation is less than 5 %, at $St \approx 2.0$, and around 2 % for the most unstable frequency $St \approx 5.0$. Thus, the vortex dynamics and the multiple tones seem to be triggered by linear mechanisms. The pseudospectrum, obtained from the resolvent analysis, is shown as a contour plot in logarithmic scale of the leading singular value from the SVD according to (2.7). The input–output amplification ratio depends on both resonance and pseudoresonance (see (2.12)) such that peaks appear when approaching an eigenvalue. The pseudoresonance levels depend on the mutual excitation of eigenvectors with more sensitive eigenvalues presenting higher peaks. In this sense, it is possible to see in figure 12 that higher frequencies are more sensitive compared with the lower frequencies. Moreover, the stable eigenvalues may affect the flow dynamics in terms of transient energy amplification given their sensitivities to disturbances.

The most unstable frequencies of $St \approx 4.5$, $5.0$ and $5.5$ are observed in the LES on the shear-layer roll-up region at $x=0.64$, as illustrated by figure 10(b). The interaction among multiple frequencies of the flow instabilities and the vortex merging reduce the shedding frequency in the LES, where the dominant tonal peak becomes $St \approx 3.5$. This nonlinear phenomenon is captured by the LES but not by the linear analysis. A more detailed discussion regarding the necessary conditions for vortex merging is presented in § 3.6.

The modal shape of each frequency is crucial to understand the system dynamics and to identify amplification regions within the flow. In this sense, figure 13(a)–13(c) present the real part of the global stability modes for the most unstable frequency $St = 5.08$ in terms of $u'$, $v'$ and $p'$, respectively. The modes are normalised with respect to the maximum value for each variable and the magnitude doubles every level to better represent lower values. The modal shapes computed for other relevant frequencies in the spectrum (resonances) show similar patterns compared with that described here and differences are only related to their characteristic wavelengths. Along the separation bubble, the modal structures of $u'$ and $v'$ are tilted against the mean shear, suggesting an Orr mechanism for transient growth of energy and amplification of disturbances (Schmid & Henningson Reference Schmid and Henningson2001). After flow reattachment, the structures become more aligned with the wall-normal direction. The pressure disturbances $p'$ display upstream travelling acoustic waves radiated from the trailing edge due to scattering mechanism. The modes displayed in the figure originate as shear layer instabilities on the airfoil suction side and extends along the wake. Hence, wake–boundary layer coupling mechanisms cannot be discarded.

Figure 13. Global stability modes of the most unstable frequency $St = 5.08$ for primitive variables (a) $u'$, (b) $v'$ and (c) $p'$.

The dominant resolvent modes are computed along the neutral stability axis $(\omega _i = 0.0)$ for $St = 5.08$ in terms of kinetic energy $k$ and presented in figure 14 normalised with respect to their maximum value. The response mode, shown in white–purple contours, depicts the location where disturbances are more energetically relevant. Here, its modal shape magnitude is presented such that it doubles every two levels. It is possible to see negligible levels from the leading edge until the recirculation bubble. Then, for $x > 0.4$, its magnitude increases quickly, indicating that the suction side bubble is an amplifier of disturbances. The forcing mode, upper-left plot with white–blue contours, highlights the most receptive location, where minimal disturbances result in larger transient growth by the system. This mode is related to the adjoint operator of the LNS equations and it is introduced in the context of airfoil secondary tones by Fosas de Pando et al. (Reference Fosas de Pando, Schmid and Sipp2017). In the present results, the leading-edge region on the suction side shows the higher values of forcing modes. Furthermore, these modes are absent on the bottom side which corroborates to the absence of pressure side-driven events for this flow configuration.

Figure 14. Response (white–purple contours) and forcing (upper-left plot with white–blue contours) modes of kinetic energy $k$ from the resolvent analysis along the neutral stability axis for $St = 5.08$.

3.5. Acoustic feedback loop mechanism

As discussed by several authors (Tam Reference Tam1974; Lowson et al. Reference Lowson, Fiddes and Nash1994; Desquesnes et al. Reference Desquesnes, Terracol and Sagaut2007; Jones & Sandberg Reference Jones and Sandberg2011; Fosas de Pando et al. Reference Fosas de Pando, Schmid and Sipp2014b), airfoil flows at transitional Reynolds numbers are subject to an acoustic feedback loop mechanism that is related to the multiple tones. In this feedback process, hydrodynamic perturbations are excited in the vicinity of the leading edge and convected downstream. The disturbances amplify along the recirculation bubble on the airfoil surface and, upon reaching the trailing edge, scatter acoustic waves that travel upstream and trigger new disturbances. In this context, figure 15(a)–15(h) present results from the resolvent analysis for different frequencies. The real part of the pressure forcing modes is shown in red–blue contours whereas black–white contours display the real component of the leading pressure response modes. The modes have been normalised with respect to their maximum values. To highlight the most receptive locations for each individual frequency, the yellow spots in the forcing modes are shown only for regions where the magnitude reaches higher values than 98 % of the maximum. As presented in figure 15, the locations of maximum receptivity change with frequency and vary along the interval $0.10 < x < 0.18$.

Figure 15. Real component of pressure response (black–white contours) and forcing (blue–red contours) modes from resolvent analysis along the neutral stability axis. The yellow spots represent the most sensitive regions where the forcing modes achieve at least 98 % of the respective maximum values for each frequency.

Aspects such as the amplitude and phase between the acoustic waves and flow receptivity at different frequencies impact the onset of hydrodynamic disturbances. To understand such complex interrelation, the acoustic feedback is analysed using the mean flow perturbation technique to solve the LNS equations around the 3-D mean flow in time domain (Jones & Sandberg Reference Jones and Sandberg2011; Fosas de Pando et al. Reference Fosas de Pando, Schmid and Sipp2014b). The method assumes that the base flow is steady and that it is not modified by the linear perturbations. The dynamics of the pressure fluctuations is presented in figure 16. For the initial condition, a pressure disturbance is applied at the leading edge, from $x = 0.0$ to $0.005$ over a short duration of $\Delta t = 1 \times 10^{-4}$ to excite all frequencies (impulse response). This triggers a wavepacket that is advected by the mean flow along the suction side. Figures 16(a) and 16(b) present the growth of disturbances for $x > 0.4$, where spatial amplification described by the response modes becomes important, as shown in figure 14. When the wavepacket reaches the trailing edge, acoustic waves are generated and travel upstream as shown in figure 16(c). After the wavepacket reaches the wake, hydrodynamic disturbances are no longer observed on the suction side, as displayed by figure 16(d). Afterwards, disturbances in the wake slowly decay whereas a new wavepacket amplifies on the suction side (figure 16e) and ( f). Similarly to the low frequency observed in the LES calculation, the wavepackets have a period of $\Delta t = 2.0$ and the next cycle is presented in figure 16(g)–16( j). The combined response from the suction side wavepacket, wake instability and upstream travelling acoustic waves keeps the fluctuation field active, amplifying the globally unstable frequencies in the eigenspectrum of figure 12, which ultimately become dominant. Readers are referred to the movie provided as supplementary movie 4 presenting the evolution of the linearised flow dynamics.

Figure 16. Snapshots of the LNS equations presented in terms of pressure fluctuations show periodic wavepackets composed by the multiple frequencies from the eigenspectrum of figure 12.

The feedback loop mechanism is investigated here by analysing the generation of flow instabilities by upstream propagating acoustic waves, as presented in figure 17. In this figure, the entropy measure ${p}/{\rho ^{\gamma }}$ is given by red–blue contours whereas pressure fluctuations are given by blue–green–red lines, where solid and dashed lines are positive and negative values, respectively. The entropy measure is used to partially filter out fluctuations associated to acoustic waves whereas pressure is used to highlight acoustic waves. In figure 17(a), it is possible to see an incoming acoustic wave at $t = 5.888$ that, upon reaching the leading edge at $t = 5.920$, triggers an entropy fluctuation due to the secondary diffraction. This latter phenomenon is typical of airfoil noise as discussed by Miotto, Wolf & de Santana (Reference Miotto, Wolf and de Santana2017). The entropy fluctuation at the leading edge, presented in red colour and highlighted by a dotted line box, is propagated downstream in figure 17(b–d) at $t = 5.920$, $5.952$ and $5.984$, respectively. This disturbance overlaps with an incoming entropy wave moving upstream, carried by an acoustic wave depicted with blue dashed lines. Then, in figure 17(e) and 17( f) at $t = 6.016$ and $6.048$, respectively, the downstream propagating entropy fluctuation encounters a second positive acoustic wave in the region where the forcing modes are maximum, i.e. for $0.10 < x < 0.18$. This upstream propagating acoustic wave carries a positive entropy fluctuation which impinges on that generated at the leading edge. Thus, although the onset of instabilities occurs very close to the leading edge, the interaction between upstream travelling acoustic waves and downstream propagating boundary layer instabilities cannot be discarded because it occurs along the entire sensitive region of the flow. Albeit the analysis is conducted for pressure and entropy, local velocity fluctuations also occur and contribute to the incoming perturbations seen by the bubble. This overall process of the feedback loop mechanism is better visualised in supplementary movie 5.

Figure 17. Snapshots of the LNS equations presented in terms of entropy (contour) and pressure (lines) fluctuations. A downstream propagating entropy wave (highlighted by dotted line box) is generated due to leading-edge secondary diffraction. This wave impinges an upstream propagating entropy fluctuation carried by an acoustic wave at the region of maximum receptivity.

Flow disturbances are tracked along the black dashed line in figure 17 (also shown as a blue dashed line in figure 3b) and presented as a function of time and space in figures 18(a) and 18(b). The former shows pressure fluctuations $p'$ whereas the latter displays disturbances of an entropy measure $({p}/{\rho ^{\gamma }})'$. In these plots, the values are normalised with respect to the maximum and presented in a logarithmic scale. The positive and negative values are presented as red and blue colours, respectively. The first wavepacket shown in figure 16(a,b) is observed travelling downstream with a local mean velocity $\bar {u}$ as bottom-up contours starting at $t = 0.0$. Upon reaching the trailing edge, at $t > 1.2$, the wavepacket generates acoustic waves propagating upstream with $\bar {u} - a$ speed. These waves are observed as top-down contours with lower magnitudes. The acoustic pressure has a phase opposition of ${\rm \pi}$ compared with the hydrodynamic fluctuations on the trailing edge and, hence, an incident negative hydrodynamic pressure fluctuation (blue) creates a scattered positive acoustic wave (red).

Figure 18. Space–time map of linear solution obtained by the mean flow perturbation for (a) pressure and (b) entropy. The map is normalised with respect to the maximum value and presented in a logarithmic scale. The positive and negative fluctuations are indicated by red and blue colours, respectively.

Upstream of $x \approx 0.4$, the acoustic waves dominate and it is not possible to see the onset of instabilities. Hence, a measure of entropy $({p}/{\rho ^{\gamma }})'$ is shown in figure 18(b) to partially filter the upstream acoustic disturbances and highlight the hydrodynamic content. In this figure, the contours of hydrodynamic fluctuations from bottom-up are better visualised. In both plots, a green region covering the entire period is placed at $0.1 \le x \le 0.18$, illustrating the maximum forcing region from figure 15. Along this region, disturbances generated in the vicinity of the leading edge ($x \approx 0.0$) travel downstream and appear to interact with the incoming acoustic waves, as depicted in figure 17(e) and 17( f). Such interaction results in a chessboard-like interference pattern where the entropy levels carried by upstream-propagating acoustic waves (inside the boundary layer) are of the same order of the entropy disturbances generated at the leading edge. We conjecture that the simultaneous combination of acoustic and hydrodynamic interactions at this location results in the maximum forcing. Finally, black lines are drawn on the plots using the convective velocity information for both pressure and entropy disturbances. These lines are used to track the feedback dynamics and show that, if the feedback indeed closes along the most receptive region, the period of $\Delta t \approx 2.0$ is satisfied.

The analysis of the feedback mechanism for the LES results is presented based on the RMS values of either the pressure $p$ or the entropy measure ${p}/{\rho ^{\gamma }}$ averaged along the $z$-direction (spanwise direction). Similarly to the linear analysis, time signals are extracted along the blue line in figure 3(b) and the RMS values are presented in a logarithmic scale in figure 19(a) for pressure and figure 19(b) for the entropy measure. In both cases, it is possible to see high fluctuation values for $x > 0.4$ travelling downstream towards the trailing edge. For $x < 0.4$, smaller values of $p'$ propagate upstream towards the leading edge. Similarly to the linear analysis, the former and latter disturbances represent hydrodynamic and acoustic waves, respectively. The entropy measure partially filters the acoustic waves moving upstream. Based on linear analysis results, the onset of disturbances occurs very close to the leading edge in a position that coincides with the small hump observed in figure 4 for pressure and friction coefficients in terms of RMS values $C_{p_{{RMS}}}$ and $C_{f_{{RMS}}}$, respectively. Thus, the wave secondary diffraction at the leading edge excites boundary layer disturbances which are also observed in the LES. The entropy fluctuations generated at the leading edge appear to interact with the upstream-propagating acoustic waves in the region of maximum receptivity, similarly to the phenomenon observed in the linear analysis. In figure 19, black lines are used to track disturbances assuming that the feedback mechanism takes place at $0.1 < x < 0.18$, indicated by the green shaded rectangle which represents the region of maximum receptivity from figure 15.

Figure 19. RMS values along the spanwise direction computed as a function of chordwise position $x$ and time $t$ for (a) pressure $p'$ and (b) entropy $(p/p^{\gamma })'$.

As a final remark, the repeating patterns observed in the simulations demonstrate that acoustic feedback occurs in the present flow. Results indicate that the loop depends on the leading-edge secondary diffraction and the region of maximum sensitivity, located downstream of the leading edge and upstream of the separation bubble. However, the intermittent interaction of vortex merging and bursting on the suction side may eventually disrupt the cycle by altering the phase and magnitude of the tonal frequencies with a temporary impact on the feedback loop.

3.6. On vortex merging and phase interference

From the previous sections, it is observed that the acoustic feedback loop is self-sustained by strong acoustic waves scattered from coherent flow structures advected past the trailing edge. These upstream-propagating acoustic waves create new flow instabilities which are amplified by the separation bubble and undergo a process of vortex pairing. Thus, it is important to understand which circumstances lead to generation of coherent structures or small-scale eddies, as discussed in § 3.3. For this task, the dynamics of wavepackets in the linear simulation is first investigated, followed by a similar analysis in terms of the LES data.

The amplification of the wavepacket along the recirculation bubble results in a maximum value of the perturbations evaluated by the mean flow perturbation at $x = 0.72$. The temporal signal of $p'$ at this location is presented in figure 20(a) depicting three envelopes. These are evaluated using the Hilbert transform to obtain the imaginary part and, thus, the magnitude of a real signal. Then, using the CWT, it is possible to extract the phase information of the previous signal. To highlight the relevant periods of the dynamics, the phase is weighted by the magnitude of the CWT coefficients as presented in figure 20(b). Comparing the temporal signal with the weighted phase, it is possible to see that the wavepacket envelopes peak when there is phase alignment across the multiple frequencies of the eigenspectrum shown in figure 12. Hence, constructive interference of multiple modes is crucial for maximum energy amplification. When the waves are out of phase, the wavepacket magnitude drops.

Figure 20. Wavepacket dynamics from linear solution including (a) temporal signal and (b) its phase scalogram at point of maximum amplitude ($x = 0.72$).

The phase information from the LES data is presented together with the spanwise-averaged pressure fluctuations in figures 21(a) and 21(b) at $x = 0.64$. This location is representative of the vortex pairing region. These figures show that high-pressure disturbances depend on phase alignment of frequencies $4 \lesssim St \lesssim 6$. This frequency range corresponds to that where the most amplified modes from the linear analysis are observed. If more (fewer) frequencies are aligned, a stronger (weaker) pressure signal is observed. If the disturbances are in phase, the result is vortex merging and strong spanwise coherence. On the other hand, if they are out of phase, the vortex pairing fails and coherence is reduced, leading to lower values of spanwise-averaged pressure fluctuations. The repeating patterns in the pressure signal show that the feedback mechanism has a period of $\Delta t \approx 2.0$, related to the lower tone in the spectrum at $St = 0.5$.

Figure 21. Effects of constructive/destructive interference across multiple frequencies presented as the (a) phase-weighted scalogram and its effect in the (b) spanwise-averaged pressure fluctuations.

Destructive and constructive interference of vortical structures during the pairing process leads to an amplitude modulation of the signal (Desquesnes et al. Reference Desquesnes, Terracol and Sagaut2007; Pröbsting et al. Reference Pröbsting, Serpieri and Scarano2014; Ricciardi et al. Reference Ricciardi, Arias-Ramirez and Wolf2020). The modulation mechanism from the 2-D simulations performed in these references differs from the current 3-D case, where turbulent transition occurs. Here, the destructive interference leads to vortex breakdown and smaller pressure fluctuations. On the other hand, constructive interference of multiple frequencies creates spikes in the pressure signal as shown for certain time instants in figure 21 and also in figures 9(a) and 9(c).