4.1. Validation against experiment for steady flow

In order to validate the formulation, particularly justifying the assumptions of the cubic velocity profile in the supercritical region and the lubrication flow in the subcritical region, we first compare our predictions against experiment for the steady circular jump. In this case, we set $W = 1$. Comparison between our predictions and the measurements of Duchesne et al. (Reference Duchesne, Lebon and Limat2014) is reported in figure 3 for the film thickness distribution in the super- and subcritical regions for silicon oil (20 cSt). The data are reproduced here in dimensionless form from their figure 2, corresponding to Re = 169, Fr = 16.88, We = 339 and a normalised disk radius ${\bar{r}_\infty } = 16.95$. The theoretical value of the thickness at the edge of the disk was fixed to ${\bar{H}_\infty } = 4.6$, corresponding to a contact angle ${\theta _Y} = {53^ \circ }$. Figure 3 shows that the theoretical predictions are generally in close agreement with the measurements of Duchesne et al. (Reference Duchesne, Lebon and Limat2014), slightly underestimating the measured thickness in the supercritical region. The location of the jump is predicted accurately whereas the jump height is slightly higher than experiment.

Figure 3. Comparison in terms of the free-surface profile between theoretical predictions and measurements of Duchesne et al. (Reference Duchesne, Lebon and Limat2014) for silicon oil (20 cSt). Results are plotted in dimensionless form for Re = 169, Fr = 16.88, We = 339 and ${\bar{r}_\infty } = 16.95$.

4.2. The transient response of the flow in the developing boundary-layer region

The time interval $\bar{t} \le 0$ corresponds to the initial steady state where $W = 1$. In this case, the initial steady-state profiles of the boundary-layer thickness and the film height are (Wang & Khayat Reference Wang and Khayat2018)

(4.2a,b)\begin{equation}\bar{\delta }(\bar{r} < {\bar{r}_0},\bar{t} \le 0) = 2\sqrt {\frac{{70}}{{39}}\bar{r}} ,\quad \bar{h}(\bar{r} < {\bar{r}_0},\bar{t} \le 0) = \frac{1}{4}\left( {\frac{2}{{\bar{r}}} + \sqrt {\frac{{210}}{{13}}\bar{r}} } \right).\end{equation}

We note that (4.2a) and (4.2b) constitute the leading-order terms in (3.14) and (3.15), respectively, for $W = 1$. Consequently, the initial conditions (3.12c) and (3.13c) are now given as

(4.3a,b)\begin{equation}{Z_0}(\bar{r}) = \frac{{280}}{{39}}{\bar{r}^3},\quad {Y_0}(\bar{r}) = \frac{1}{4}\left( {2 + \sqrt {\frac{{210}}{{13}}} {{\bar{r}}^{3/2}}} \right).\end{equation}

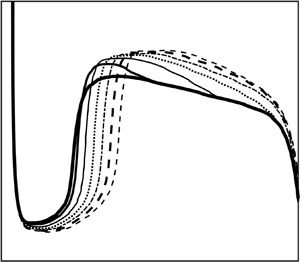
Figure 4 illustrates the transient development of the boundary-layer thickness and the film height in the developing boundary-layer region at equal time intervals, subject to the jet velocity profile (4.1). Shown is the numerical solution for $\bar{\delta }(\bar{r},\bar{t})$ and $\bar{h}(\bar{r},\bar{t})$, which closely agrees with their approximate counterparts established earlier in (3.14) and (3.15), to leading order. In this case, (3.9a) reduces essentially to the familiar steady-state form: $\bar{h}(\bar{r},\bar{t}) = {\textstyle{3 \over 8}}\bar{\delta }(\bar{r},\bar{t}) + 1/2\bar{r}$ (Wang & Khayat Reference Wang and Khayat2018). At $\bar{t} = 0$, W = 1, and the classical boundary-layer result is recovered (Watson Reference Watson1964; Schlichtling & Gersten Reference Schlichtling and Gersten2000). The profiles in figure 4 do not show a deviation from the classical parabolic character of the boundary-layer height, as the jet accelerates. We observe that since the boundary-layer height is small near the origin, the film height decays like $\bar{h}\sim 1/2\bar{r}$, regardless of the jet velocity value. This behaviour is also reflected by the $\bar{h}$ curves in figure 4, showing a narrow spread as time varies compared with $\bar{\delta }$. In particular, the $\bar{h}$ curves tend to saturate near impingement. Accelerating the jet tends to lower both the boundary-layer height and the film thickness with time. Therefore, the jet acceleration has a similar effect of thinning the boundary layer as with slip (Prince et al. Reference Prince, Maynes and Crockett2012; Khayat Reference Khayat2016), disk rotation (Wang & Khayat Reference Wang and Khayat2018) and gravity for high-viscosity liquids (Wang & Khayat Reference Wang and Khayat2019). Figure 4 also suggests that $\bar{\delta }(\bar{r},\bar{t})$ and $\bar{h}(\bar{r},\bar{t})$ do not exhibit a long-term transient behaviour after the acceleration period ends $(\bar{t} \ge {\bar{t}_c})$; that is, the flow reaches the steady state the moment the acceleration is halted. We shall see that this is not the case for the flow in the fully developed viscous region.

Figure 4. The transient behaviour of the developing boundary-layer region for a linearly accelerated jet. The rescaled boundary-layer height, $\bar{\delta }(\bar{r},\bar{t})$, and film thickness, $\bar{h}(\bar{r},\bar{t})$, are plotted against the rescaled radial distance $\bar{r}$. The flow is examined subject to the jet velocity profile (4.1) for $A = 0.022$ and ${\bar{t}_c} = 50$. The curves $\bar{t} \ge 50$ represent the final steady-state profile for $\bar{\delta }$ and $\bar{h}$. The transition location coincides with the intersection of the two heights (at the cusps in the figure), indicated here by vertical lines. The blue curve represents the locus of the transition points demarking the end of the developing boundary-layer region at different times.

It is worth mentioning that the overall monotonic thinning behaviour of the film in this region due to the jet acceleration resembles the monotonic thinning behaviour of a fluid film lying on an accelerated stretching surface in the plane (Wang Reference Wang1990) and for axisymmetric flow (Usha & Sridharan Reference Usha and Sridharan1995). In those studies, a similarity solution was developed for the inversely linear unsteady (accelerating and decelerating) stretching. The actual film thickness evolution was found to be inversely proportional to the square root of the imposed stretching velocity. This behaviour is similar to the dependence of the film thickness evolution on the jet velocity at large radial positions depicted in figure 4.

We note that the behaviour of $\bar{\delta }$ in figure 4 can also be deduced qualitatively from a balance argument from (3.4). By taking u to correspond to the free-surface value W $(u\sim W)$, the transient term $Re\,{u_t}$ cancels out with the radial pressure gradient term reflected by $Re\,\dot{W}$. Thus, the radial convective term and the viscous term must balance in (3.4): $Re\,u{u_r}\sim Re\,{W^2}/r$, leading to $\delta \sim \sqrt {r/W\,Re} $ or $\bar{\delta }\sim \sqrt {\bar{r}/W} $ which is in accordance with the leading-order term in (3.14).

The evolution of $\bar{\delta }(\bar{r},\bar{t})$ and $\bar{h}(\bar{r},\bar{t})$ is illustrated in figure 5 at different radial positions in the developing boundary-layer region. In particular, the evolution of $\bar{\delta }$ at small time is compared against the developed approximate solution (A10) given in Appendix A, showing a good agreement for $\bar{t} < 1$ (see inset). In general, $\bar{h}$ decreases more slowly than $\bar{\delta }$; however, both $\bar{h}$ and $\bar{\delta }$ decrease at a lower rate with time as the jet accelerates. This behaviour can be inferred from ${\bar{h}_{\bar{t}}}\sim {\textstyle{3 \over 8}}{\bar{\delta }_{\bar{t}}}\sim{-} {\textstyle{3 \over 8}}{(1 + At)^{ - 3/2}}$ to leading order.

Figure 5. Evolution of the boundary-layer and film heights at different radial positions in the developing boundary-layer region for $A = 0.022$ and ${\bar{t}_c} = 50$. The green dashed vertical line indicates the time ${\bar{t}_c} = 50$ at which the jet velocity as well as the boundary-layer and film heights all reach their final steady state. The inset shows a comparison for the evolution of the boundary-layer thickness at small time between the numerical solution (black curves) and approximate solution (A10) (blue curves).

Figure 6 depicts the evolution of the transition location ${\bar{r}_0}(\bar{t})$ and corresponding film thickness ${\bar{h}_0}(\bar{t}) \equiv \bar{h}(\bar{r} = {\bar{r}_0})$. As the jet accelerates (inertia is enhanced), the transition point moves further downstream from impingement, and the corresponding film thickness decreases, but they both reach their final steady state at $\bar{t} = {\bar{t}_c}$. In fact, this behaviour can be deduced analytically by equating the leading-order terms in (3.14) and (3.15), yielding ${\bar{r}_0}(\bar{t}) \approx {({\textstyle{{78} \over {875}}}W)^{1/3}}$ or ${\bar{r}_0}(\bar{t}) \propto {W^{1/3}}$. Moreover, the relation $\bar{h}(\bar{r},\bar{t}) = {\textstyle{3 \over 8}}\bar{\delta }(\bar{r},\bar{t}) + 1/2\bar{r}$, established earlier, reduces to ${\bar{h}_0} = 4/5{\bar{r}_0}$ at the transition point, suggesting that ${\bar{h}_0}(\bar{t}) \propto {W^{ - 1/3}}$. For the initial steady state $(\bar{t} \le 0)$, since $W = 1$, we obtain ${\bar{r}_0} = {(78/875)^{1/3}} = 0.447$ and ${\bar{h}_0} = 1.791$, which are the values reflected in figure 6 at $\bar{t} = 0$. In comparison, Watson's steady transition point found using an exact solution of the boundary-layer equations is given as ${\bar{r}_0} = {(9\sqrt 3 c({\rm \pi} - c\sqrt 3 )/16{{\rm \pi} ^2})^{1/3}} = 0.463$, where $c = 1.402$ (Watson Reference Watson1964), which reflects a discrepancy of less than 3 %.

Figure 6. Evolution of the location and film thickness at the transition point between the developing boundary-layer and fully developed viscous regions for $A = 0.022$ and ${\bar{t}_c} = 50$. The green dashed vertical line indicates the time ${\bar{t}_c} = 50$ at which W, as well as ${\bar{r}_0}$ and ${\bar{h}_0}$ all reach their final steady state.

The pressure distribution $p(\bar{r},\bar{t})$ in the developing boundary-layer region is shown in figure 7. Here, we neglect the effect of gravity in the supercritical region. Therefore, expressions (3.3) and (3.17) reduce to $p(0 < r < {r_0},t) = ({r_0} - r)\dot{W}$ and $p({r_0} \le r \le {r_J},t) = 0$, respectively. Figure 7 indicates that the pressure in this region decreases linearly with the radial distance at different times for $\bar{t} \le {\bar{t}_c}$ and vanishes at the transition point. This linear decrease in the pressure follows a constant radial pressure gradient at all times because of the linear acceleration of the jet. The behaviour shown in figure 7 can be interpreted analytically by expressing the pressure, using (3.3), to obtain, to leading order: $p(\bar{r} < {\bar{r}_0},0 < \bar{t} < {\bar{t}_c}) = A({\bar{r}_0} - \bar{r}) \approx A[{({\textstyle{{78} \over {875}}}(1 + A\bar{t}))^{1/3}} - \bar{r}]$. As depicted in the inset of figure 7, for a given radial position, the beginning and the end of the acceleration period are accompanied by a sudden jump and a sudden drop in the pressure, respectively. However, during the acceleration period, the pressure increases nonlinearly with time. This behaviour resembles the one reported by Chang & Maxey (Reference Chang and Maxey1995) for the case of a linearly accelerated flow over a sphere, from one steady state to another (see their figure 6). They attributed the sudden changes in pressure to the added-mass effects, i.e. inertial effects added to the system because of the acceleration, which is the same driving mechanism of the transient response in the present problem.

Figure 7. The transient response of the pressure in the developing boundary-layer region for a linearly accelerated jet ($A = 0.022$ and ${\bar{t}_c} = 50$). The curve $\bar{t} > 50$ indicates that $p = 0$ is the final steady state. The blue curve represents the locus of the transition points. The inset depicts the evolution of the pressure at different radial positions showing sudden changes at the beginning and at the end of the acceleration period.

4.3. The transient response of the flow in the fully developed viscous region

We now examine the flow response in the fully developed viscous region subject to the jet velocity profile (4.1). The initial steady-state profiles of the film thickness and the surface velocity are recalled as (Wang & Khayat Reference Wang and Khayat2018)

(4.4a)\begin{gather}\bar{h}({\bar{r}_0} < \bar{r} < {\bar{r}_J},\bar{t} \le 0) = \frac{{175}}{{136}}{\bar{r}^2} + \frac{{233}}{{340\bar{r}}} = \frac{{175}}{{136\bar{r}}}({\bar{r}^3} - \bar{r}_0^3) + 2\frac{{{{\bar{r}}_0}}}{{\bar{r}}}\sqrt {\frac{{70}}{{39}}{{\bar{r}}_0}}, \end{gather}

(4.4b)\begin{gather}s({\bar{r}_0} < \bar{r} < {\bar{r}_J},\bar{t} \le 0) = \frac{4}{{5\bar{h}\bar{r}}}.\end{gather}

We note that (4.4a) and (4.4b) are in close agreement with Watson's expressions, reproduced here in dimensionless forms as: $\bar{h} \approx 1.28{\bar{r}^2} + 0.69/\bar{r}$ and $s \approx 0.81/\bar{h}\bar{r}$ (Watson Reference Watson1964), respectively.

The time-dependent boundary-layer height and supercritical film thickness are plotted against the radial distance at equal time intervals as shown in figure 8. We recall that the transition point moves downstream with time, as the jet accelerates. At any time, the film thickness exhibits a strong minimum followed by an increase with the radial distance. In the limit $\bar{t} = 0$, (4.4a) indicates that the height increases like $\bar{h} \propto {\bar{r}^2}$ at large distance. For a faster jet, the film acquires additional radial momentum, with a reduced viscous effect. Therefore, it is apparent from figure 8 that, as the jet accelerates, the minimum film thickness weakens, accompanied by an overall thinning of the boundary layer and film. We observe that, close to the transition point, the film thickness in the fully developed viscous region decays at a slower rate at a later time than initially, a behaviour similar to that predicted in the boundary-layer region (see figure 5). Figure 8 indicates that the location of the minimum height moves downstream as the effect of viscosity gradually diminishes with time relative to inertia. The last point along the $\bar{h}$ curves marks the end of the fully developed viscous region at different times, coinciding with the jump occurrence.

Figure 8. Transient response of the developing boundary-layer height and film thickness in the supercritical region for a linearly accelerated jet ($A = 0.022$ and ${\bar{t}_c} = 50$). The red curve represents the locus of the jump points (also indicated by the vertical lines) demarking the end of the fully developed viscous region at different times. The cyan curve represents the quasi-steady profile of the film thickness in the fully developed viscous region at $\bar{t} = 10$. Also indicated in vertical lines on the left are the transition point locations at different times. The curve $\bar{t} > 50$ represents the final steady-state profile of $\bar{\delta }$ and $\bar{h}$. The jump is determined for $Re = 100$, $Fr = 10$, $We = 120$, ${\bar{H}_\infty } = R{e^{1/3}}{H_\infty } = 5.1$ and ${\bar{r}_\infty } = R{e^{ - 1/3}}{r_\infty } = 5.38$.

We find that, far from the transition point, the actual instantaneous film thickness in the fully developed viscous region deviates from the quasi-steady state, and so does the jump location. We illustrate this deviation by adding the quasi-steady profile (in cyan) for $\bar{t} = 10$ in figure 8. We also observe from the figure that the film thickness continues to decrease after the acceleration has ceased at $\bar{t} = {\bar{t}_c} = 50$. Thus, unlike the developing boundary-layer region, the film thickness in the fully developed viscous region exhibits a long-term transient behaviour, which is particularly evident at large $\bar{r}$; the thickness profile reaches its final steady state at a time $\bar{t} > {\bar{t}_c}$. This suggests that, despite the end of the acceleration period, inertial effects still induce a transient change in the flow, which is attributed to the intrinsic nonlinearities present in (3.22a) and (3.22b).

Figure 9 shows the evolution of the film thickness $\bar{h}(\bar{r},\bar{t})$ in the fully developed viscous region at different radial positions. The quasi-steady states are also plotted (cyan curves) for comparison. It is shown that, initially, the actual instantaneous film thickness accumulates and deviates from the quasi-steady state given the significance of viscous effects (Telionis Reference Telionis1981), exhibiting a weak maximum when inertia becomes as important as viscous effects. The thickness then decays with time as inertia becomes dominant, and behaves closer to the quasi-steady state as reflected by the narrowing of the gap between the black and cyan curves in figure 9. The purple curve, representing the locus of the maximum film thickness at different radial positions, shows an earlier occurrence of this maximum at smaller $\bar{r}$. This transient behaviour of the film thickness (early-stage maximum before decaying with time) is similar to the one observed in the case of a laminar film suddenly accelerated by gravity and falling inside a vertical circular tube as studied experimentally by Zhong et al. (Reference Zhong, He and Longtin2020) (see their figure 9). Furthermore, we observe that the film thickness reaches its final steady state at $\bar{t} \approx {\bar{t}_c}$ for small $\bar{r}$, and at $\bar{t} > {\bar{t}_c}$ for large $\bar{r}$, as reflected by the green solid curves in figure 9 and the inset, respectively, suggesting that the long-term transient response in the film thickness is particularly evident at large $\bar{r}$.

Figure 9. Evolution of the film thickness in the fully developed viscous region at different radial positions for $A = 0.022$ and ${\bar{t}_c} = 50$. The purple curve represents the locus of the maximum film thickness, the cyan curves represent the quasi-steady film thickness profiles and the green solid curve represents the locus of the final steady state. The inset depicts the evolution of $\bar{h}$ at large radial positions for $\bar{t} > 40$, showing that the final steady state is reached at $\bar{t} > {\bar{t}_c}$.

As discussed earlier (figure 8), the parabolic profile of the film thickness in the fully developed viscous region exhibits a minimum at any time. The time variation of this minimum film thickness, denoted by ${\bar{h}_{min}}(\bar{t})$, and its corresponding radial position, denoted by ${\bar{r}_{min}}(\bar{t})$, are plotted in figure 10. At the early stage of the flow, as viscous effects are important, ${\bar{h}_{min}}$ exhibits a weak maximum, while ${\bar{r}_{min}}$ exhibits a weak minimum. As viscous effects gradually diminish with time relative to inertia, the minimum film height weakens and occurs further downstream.

Figure 10. Evolution of the minimum film thickness and its corresponding radial position in the fully developed viscous region for $A = 0.022$ and ${\bar{t}_c} = 50$.

The transient behaviour of the supercritical free-surface velocity is depicted in figure 11. As seen in figure 11(a), at any time, the surface velocity remains equal to the jet velocity in the developing boundary-layer region, as reflected by the horizontal lines, before it decreases monotonically with distance downstream of the transition location in the fully developed viscous region. At $\bar{t} = 0$, the monotonic decrease of s with respect to $\bar{r}$ is recalled from the initial steady-state solution by substituting (4.4a) into (4.4b)

(4.5)\begin{equation}s({\bar{r}_0} < \bar{r} < {\bar{r}_J},\bar{t} \le 0) = \frac{4}{5}{\left( {\frac{{175}}{{136}}({{{\bar{r}}^3} - \bar{r}_0^3} )+ 2{{\bar{r}}_0}\sqrt {\frac{{70}}{{39}}{{\bar{r}}_0}} } \right)^{ - 1}}.\end{equation}

In this case (at $\bar{t} = 0$), s decreases like ${\bar{r}^{ - 3}}$ at large distance, and we can clearly observe from figure 11(a) a similar behaviour at subsequent times. We can also see that the jet acceleration increases the surface velocity of the flow with time (see figure 11b), but diminishes the rate at which it decreases with radial distance (see figure 11a), which is similar to the effect of slip (Prince et al. Reference Prince, Maynes and Crockett2012; Khayat Reference Khayat2016) and disk rotation (Wang & Khayat Reference Wang and Khayat2018). We observe that s = W at $\bar{r} = 0.3$ in figure 11(b), since this radial position belongs to the developing boundary-layer region at all times. Figure 11(b) and the inset in figure 9 show that, similar to the film thickness, the long-term transient behaviour of the surface velocity in the fully developed viscous region is particularly evident at large radial positions. This is depicted by the green solid curve representing the locus of the final steady state (see for example the time at which $\bar{h}$ and s reach their final steady state for $\bar{r} = 1.7$ compared with $\bar{r} = 0.9$).

Figure 11. Transient behaviour of the supercritical surface velocity for $A = 0.022$ and ${\bar{t}_c} = 50$. The radial dependence of s is plotted at equal time intervals (a), and the evolution of s is plotted at different radial positions in the supercritical region (b). The blue curve represents the locus of the transition points whereas the red curve represents the locus of the jump points. The green solid curve represents the locus of the final steady state reached by s at different $\bar{r}$. The jump is determined for $Re = 100$, $Fr = 10$, $We = 120$, ${\bar{H}_\infty } = 5.1$ and ${\bar{r}_\infty } = 5.38$.

In figure 12, we present a three-dimensional surface plot to illustrate in detail the transient behaviour of the thin film in the fully developed viscous region. We show the evolution of both the film thickness as depicted by the height of the surface (z-axis), and surface velocity as described by the colour map. It is shown from the colour map that, upon accelerating the jet, the surface velocity at the transition location increases with time, which is also reflected by the blue curve in figure 11. However, the surface velocity does not change much at the hydraulic jump location, which is also reflected by the red curve in figure 11. Moreover, the projected curves in figure 12 indicate that the relative change between the final and initial steady states is larger for ${\bar{r}_J}(\bar{t})$ and ${\bar{h}_J}(\bar{t})$ than for ${\bar{r}_0}(\bar{t})$ and ${\bar{h}_0}(\bar{t})$.

Figure 12. Surface plot showing the evolution of the film thickness and surface velocity contours in the fully developed viscous region for $A = 0.022$ and ${\bar{t}_c} = 50$. The height of the surface reflects the film thickness while the colour map reflects the values of the surface velocity. The jump is determined for $Re = 100$, $Fr = 10$, $We = 120$, ${\bar{H}_\infty } = 5.1$ and ${\bar{r}_\infty } = 5.38$.

The wall shear stress at the disk is expressed as

(4.6a)\begin{gather}{\bar{\tau }_w}(\bar{r} < {\bar{r}_0},\bar{t}) = \frac{3}{2}\frac{W}{{\bar{\delta }}},\end{gather}

(4.6b)\begin{gather}{\bar{\tau }_w}({\bar{r}_0} < \bar{r} < {\bar{r}_J},\bar{t}) = \frac{3}{2}\frac{s}{{\bar{h}}}.\end{gather}

Always for the same jet velocity profile (4.1), figure 13 illustrates the transient behaviour of the wall shear stress. As seen in figure 13(a), at any time, the stress decays very rapidly with the radial distance in the developing boundary-layer region, which can be explained by referring to the leading-order solution in (3.14). In this case, (4.6a) reduces to

(4.7)\begin{equation}{\bar{\tau }_w}(\bar{r} < {\bar{r}_0},\bar{t}) \approx \sqrt {\frac{{39}}{{280}}\frac{{{W^3}}}{{\bar{r}}}} .\end{equation}

Equation (4.7) also suggests that, for a given radial position in the developing boundary-layer region, ${\bar{\tau }_w}\sim {W^{3\; /2}}$, which resembles the dependence of the wall shear stress on the stretching velocity for a fluid film lying on an unsteady stretching surface (Wang Reference Wang1990; Usha & Sridharan Reference Usha and Sridharan1995). After its rapid drop in the developing boundary-layer region, ${\bar{\tau }_w}$ exhibits a maximum in the fully developed viscous region before decaying monotonically with the radial distance as in figure 13(a). For $\bar{t} = 0$, the monotonic decrease of ${\bar{\tau }_w}$ with respect to $\bar{r}$ is recalled from the initial steady-state solution by substituting (4.4a) and (4.4b) into (4.6b) to obtain

(4.8)\begin{equation}{\bar{\tau }_w}({\bar{r}_0} < \bar{r} < {\bar{r}_J},\bar{t} \le 0) = \frac{6}{5}\bar{r}{\left( {\frac{{175}}{{136}}({{\bar{r}}^3} - \bar{r}_0^3) + 2{{\bar{r}}_0}\sqrt {\frac{{70}}{{39}}{{\bar{r}}_0}} } \right)^{ - 2}}.\end{equation}

In this case (at $\bar{t} = 0$), at large radial distance, the wall shear stress decays like ${\bar{r}^{ - 5}}$, and a similar behaviour is observed in figure 13(a) at subsequent times. Moreover, the rate at which the wall shear stress decays with radial distance increases as the jet accelerates. We observe that, since accelerating the jet causes a higher velocity gradient near the wall, we obtain a monotonic increase with time in the wall shear stress at any radial position in the supercritical region as depicted in figure 13(b). This can easily be explained by referring to (4.5a) and (4.5b), knowing that W and s increase with time, whereas $\bar{\delta }$ and $\bar{h}$ decrease overall. Figure 13(b) also shows a long-term transient response in ${\bar{\tau }_w}$ at large $\bar{r}$.

Figure 13. Transient behaviour of the supercritical wall shear stress for $A = 0.022$ and ${\bar{t}_c} = 50$. The radial dependence of ${\bar{\tau }_w}$ is plotted at equal time intervals (a), and the evolution of ${\bar{\tau }_w}$ is plotted at different radial positions in the supercritical region (b). The blue curve represents the locus of the transition points whereas the red curve represents the locus of the jump points. The green solid curve represents the locus of the final steady state reached by ${\bar{\tau }_w}$ at different $\bar{r}$. The jump is determined for $Re = 100$, $Fr = 10$, $We = 120$, ${\bar{H}_\infty } = 5.1$ and ${\bar{r}_\infty } = 5.38$.

Finally, a monotonic increase with time in the wall shear stress was also reported by Seddighi et al. (Reference Seddighi, He, Vardy and Orlandi2014) for a linearly accelerating channel flow starting from an initially statistically steady turbulent flow (see their figure 3b). However, the friction coefficient, which was introduced as the actual wall shear stress normalised relative to the instantaneous bulk velocity instead of the average velocity, showed a non-monotonic evolution (see their figure 3c). Following Seddighi et al. (Reference Seddighi, He, Vardy and Orlandi2014), we introduce the friction coefficient at the disk in the supercritical region as ${C_f} = 2R{e^{ - 2/3}}{\bar{\tau }_w}/{W^2}$ where ${C_f}$ is the actual wall shear stress normalised by ${\textstyle{1 \over 2}}\rho {V^2}(t)$, and $V(t)$ is the dimensional instantaneous jet velocity, with $V(t = 0) = {V_0}$. In this case, the friction coefficient in the developing boundary-layer and fully developed viscous regions can be expressed as

(4.9a)\begin{gather}{C_f}(\bar{r} < {\bar{r}_0},\bar{t}) = \frac{{3R{e^{ - 2/3}}}}{{W\bar{\delta }}},\end{gather}

(4.9b)\begin{gather}{C_f}({\bar{r}_0} < \bar{r} < {\bar{r}_J},\bar{t}) = \frac{{3R{e^{ - 2/3}}s}}{{{W^2}\bar{h}}},\end{gather}

respectively. Figure 14 shows the transient behaviour of the supercritical friction coefficient. We observe from figure 14(a) that, at any time, the radial dependence of the friction coefficient follows the radial dependence of the wall shear stress shown earlier in figure 13(a). Interestingly, in the fully developed viscous region, in contrast to the monotonic response of the shear stress (see figure 13b for $\bar{r} > 0.5$), ${C_f}$ exhibits a non-monotonic transient behaviour as depicted in figure 14(b). This occurs further downstream in the fully developed viscous region at the radial positions that show a weak maximum in the film thickness, namely at $\bar{r} = 0.9$, 1 and 1.1 (see also figure 9). We observe that, at these radial positions, ${C_f}$ decreases initially with the increase in the film thickness, exhibiting an early weak minimum coinciding with the weak maximum in the film thickness. As the flow continues to accelerate, the friction coefficient increases as a result of the low flow momentum that is pushed inside of the boundary layer against the wall, simultaneously reducing the overall film thickness. This non-monotonic behaviour of the friction coefficient shown in figure 14(b) is parallel to the one observed by Seddighi et al. (Reference Seddighi, He, Vardy and Orlandi2014) as reported in their figure 3(c). In their case, the friction coefficient behaves oppositely to the boundary-layer thickness, whereas in our case, the friction coefficient behaves oppositely to the film thickness.

Figure 14. Transient behaviour of the friction coefficient in the supercritical region for $A = 0.022$ and ${\bar{t}_c} = 50$. The radial dependence of ${C_f}$ is plotted at equal time intervals (a), and the evolution of ${C_f}$ is plotted at different radial positions in the fully developed viscous region (b). The blue curve represents the locus of the transition points whereas the red curve represents the locus of the jump points. The green solid curve represents the locus of the final steady state reached by ${C_f}$ at different $\bar{r}$. The jump is determined for $Re = 100$, $Fr = 10$, $We = 120$, ${\bar{H}_\infty } = 5.1$ and ${\bar{r}_\infty } = 5.38$.

4.4. Evolution of the hydraulic jump radius and comparison with the numerical simulation

A numerical simulation of a transient jet impinging over a stationary horizontal disk was carried out using the Ansys Fluent software. Silicone oil was considered with the following physical properties: $\rho = 950\;\textrm{kg}\;{\textrm{m}^{ - 3}}$, $\mu = 19\;\textrm{mPa}\;\textrm{s}$ and $\gamma = 20\;\textrm{dyn}\;\textrm{c}{\textrm{m}^{ - 1}}$. The nozzle radius was taken as $a = 1.6\;\textrm{mm}$ and the initial jet flow rate was $Q = 10\;\textrm{ml}\;{\textrm{s}^{ - 1}}$. These parameters correspond to the steady-state experiment carried out by Duchesne et al. (Reference Duchesne, Lebon and Limat2014) for a plate radius of 150 mm and a disk-to-nozzle distance of 16 mm, except that their operating flow rate was $Q = 17\;\textrm{ml}\;{\textrm{s}^{ - 1}}$. In addition, we have shortened the radius of the disk to 40 mm and the disk-to-nozzle distance to 8 mm to lower the computational cost. In terms of the dimensionless parameters, this corresponds to $Re = 100$, $Fr = 10$, $We = 120$ and ${\bar{r}_\infty } = 5.38$.

The numerical model was previously validated against the measurements of Duchesne et al. (Reference Duchesne, Lebon and Limat2014) for steady state (Wang & Khayat Reference Wang and Khayat2021). In order to study the linearly accelerated jet, the jet velocity profile (4.1) was imposed in the present numerical simulation, where A = 0.022 and ${\bar{t}_c} = 50$. The flow was allowed to fall freely over the edge of the disk in the absence of any obstacle.

As the flow is assumed to be axisymmetric, polygonal jumps (Rojas & Tirapegui Reference Rojas and Tirapegui2015) are not considered. In this case, we solve the axisymmetric version of the full Navier–Stokes equations in cylindrical coordinates (see Wang & Khayat Reference Wang and Khayat2021 for details), with the gas–liquid interface (i.e. the free surface) tracked by an extra scalar field using the volume of fluid (VOF) approach (Hirt & Nichols Reference Hirt and Nichols1981). The physical and computational domains are shown in figure 15 with the dimensions shown along the corresponding sides of the domain. The simulation is carried out using a finite volume solver (Ansys Fluent), with the primary variables located at the centroid of the mesh cells. The fluxes at the cell surface are calculated based on the interpolated values of the cell centroid. With the VOF method, the free surface is tracked by a transport equation that governs the volume fraction of the liquid phase, namely

(4.10)\begin{equation}\frac{\partial }{{\partial t}}{\alpha _l} + {\boldsymbol{v}_l}\boldsymbol{\cdot }\boldsymbol{\nabla }{\alpha _l} = 0,\end{equation}

with ${\alpha _l}$ being the volume fraction of the liquid, and therefore ${\alpha _g} = 1 - {\alpha _l}$ being the gas fraction. Here, ${\boldsymbol{v}_l}$ is the velocity vector of the liquid. With this approach, only a single set of transport equations is solved. The values of variables and fluid properties at the centroid of each cell represent the volume-weighted averages based on the fraction of the two phases.

Figure 15. The three-dimensional physical domain and the two-dimensional axisymmetric computational domain of the numerically simulated flow.

The standard Semi-Implicit Method for Pressure Linked Equations-Consistent (SIMPLEC) scheme (Van Doormaal & Raithby Reference Van Doormaal and Raithby1984) is selected for pressure correction. For spatial discretisation, we adopt the second-order Quadratic Upstream Interpolation for Convective Kinematics (QUICK) scheme (Leonard & Mokhtari Reference Leonard and Mokhtari1990), which uses two upstream and one downstream value of the neighbouring cell centroid to interpolate the face values of the control volume for flux calculation. A second-order implicit time marching scheme is selected for the best stability. Finally, the volume fraction (4.10) is discretised by a second-order compressive scheme such that the face value of the volume fraction is given by ${\phi _f} = {\phi _d} + 2\boldsymbol{\nabla }{\phi _d}\boldsymbol{\cdot }\boldsymbol{S}$, where ${\phi _f}$ is the volume fraction at the cell face between the donor (upstream) and acceptor (downstream) cell, ${\phi _d}$ is the volume fraction of the donor cell and $\boldsymbol{S}$ is the displacement vector from the donor cell centroid to the centroid of the cell face. Surface tension is considered using the continuum surface force model (Brackbill, Kothe & Zemach Reference Brackbill, Kothe and Zemach1992). The detailed reasons of these numerical choices can be found in the work of Wang & Khayat (Reference Wang and Khayat2021).

The pressure is set to atmospheric everywhere in the domain and the velocity is set to be zero initially. The domain is at first fully occupied by air, the silicon oil at a uniform velocity of flow rate Q = 10 ml s⁻¹ is injected into the domain through the inlet of radius a = 1.6 mm until the first steady state is reached when a stable hydraulic jump has been formed. Then the flow rate starts to vary according to Q = 10 + 37.3t ml s⁻¹. The impingement surface of radius R = 40 mm is at a distance D = 8 mm away from the inlet. The boundary conditions are also displayed in the computational domain. The pressure is set to be atmospheric at the right side of the computational domain (cf. figure 15). A sidewall near the trailing edge of the disk is constructed so that the flow can turn and flow off the domain under the action of gravity. We note that the upper boundary of the domain is set to a no-slip condition instead of atmospheric pressure as it turns out that overregulating the pressure sometimes drives the flow to an unrealistic state before reaching a steady state. The solution converges better when using a no-slip condition which allows the pressure to freely adjust itself according to the momentum evolution. Practically, this should not affect the solution much since the viscosity of the gas phase is usually negligible compared with that of the liquid, and the configuration is laminar. In addition, we refer to the satisfactory numerically simulated results obtained by Askarizadeh et al. (Reference Askarizadeh, Ahmadikia, Ehrenpreis, Kneer, Pishevar and Rohlfs2020) and Wang & Khayat (Reference Wang and Khayat2021), who also used a similar numerical configuration.

The convergence test is carried out at the steady state. Three sets of uniform grid sizes (the side length of the control volume) are tested, namely 0.32, 0.16 and 0.08 mm, treated as coarse, medium and fine meshes, respectively. It is found that the relative error in the jump location is well below 1 % between the medium and the fine mesh. In this case, the medium mesh size is sufficient and thus adopted in the transient numerical computation. For more details on the numerical convergence test, the reader is referred to the work of Wang & Khayat (Reference Wang and Khayat2021).

The evolution of the simulated flow in the (r, z) plane is depicted in figure 16 in terms of the volume fraction of the fluid at equal time intervals. As the jet accelerates, the location of the jump moves forward and the maximum film height increases.

Figure 16. Evolution of the simulated flow for $A = 0.022$, ${\bar{t}_c} = 50$, $Re = 100$, $Fr = 10$, $We = 120$ and ${\bar{r}_\infty } = 5.38$. The volume fraction is presented for liquid (in red) and surrounding air (in blue), corresponding to ${\alpha _l} = 1$ and ${\alpha _g} = 0$, respectively. The liquid and gas phases are separated by the free surface ($0 < \alpha < 1$).

The comparison of the free-surface height at equal time intervals between the theory and numerical simulation is shown in figure 17. Best comparison was achieved upon taking ${\bar{H}_\infty } = 5.1$. This corresponds to an edge film thickness equal to 1.76 mm, which is close to the capillary length of the considered fluid (1.46 mm). It is shown that the theory predicts well the free-surface evolution of the fluid, except the gradual transition in the hydraulic jump region, due to the sharp jump assumption, as well as the turn-around region at the edge. These issues will be touched on later in § 5.

Figure 17. Comparison between theory (black solid curves) and numerical simulation (red circles). The free-surface height is shown at equal time intervals for $A = 0.022$, ${\bar{t}_c} = 50$, $Re = 100$, $Fr = 10$, $We = 120$, ${\bar{H}_\infty } = 5.1$ and ${\bar{r}_\infty } = 5.38$.

We next quantify the comparison between the theory and numerical simulation in terms of the jump radius, the upstream and downstream jump heights, as depicted in figure 18, which show good agreement. As is apparent, even though the jet velocity increases linearly with time, the responses in ${\bar{r}_J}$, ${\bar{h}_J}$ and ${\bar{H}_J}$ are predominantly linear only at later times. We note that the jump position deduced from the numerical simulation corresponds to the maximum radial gradient in the film thickness, and the downstream jump height corresponds to the numerical maximum film thickness. Due to our sharp jump assumption, the downstream jump height predicted theoretically cannot be directly compared against the one from the numerical simulation. However, the good agreement shown in figure 18 in terms of ${\bar{H}_J}$ was obtained upon reducing all the predicted values at all times by 11 % as a correction made to compensate for the sharp jump assumption.

Figure 18. Comparison between theory (lines) and numerical simulation (points). The evolution of the jump radius ${\bar{r}_J}$, the upstream jump height ${\bar{h}_J}$ and the downstream jump height ${\bar{H}_J}$ are shown for a linearly accelerated jet for $A = 0.022$, ${\bar{t}_c} = 50$, $Re = 100$, $Fr = 10$, $We = 120$, ${\bar{H}_\infty } = 5.1$ and ${\bar{r}_\infty } = 5.38$.

Combining the simulated free-surface height at equal time intervals in one plot, as shown in figure 19, reveals an interesting transient dynamics, which is not necessarily captured by the thin-film theory. The figure indicates that the film height tends to exhibit an overshoot in the form of a localised maximum that diffuses with time. We also notice that, although the downstream film thickness increases with time, it always converges to the initial steady-state profile at a certain radial position that increases with time. In other words, the influence of inertia, as a result of the jet acceleration, on the downstream film height is not felt until later times. Moreover, we observe that the film thickness at the edge does not vary with time, as the film seems to be pinned there, making our earlier assumption of a time-independent ${H_\infty }$ in our theory plausible. The overall increase in the downstream height is obviously accompanied by a rise in the pressure force, which acts on the jump to slow it down. However, the jump continues to move outward, reflecting the dominance of inertia over the pressure force as the jet accelerates.

Figure 19. The film profiles based on the numerical simulation at equal time intervals for $A = 0.022$, ${\bar{t}_c} = 50$, $Re = 100$, $Fr = 10$, $We = 120$ and ${\bar{r}_\infty } = 5.38$.

The transient behaviour of the subcritical film thickness and surface velocity, predicted from (3.31) and (3.34), is shown in figure 20. Figure 20(a,c) shows the radial dependence of $\bar{H}$ and S at equal time intervals, whereas figure 20(b,d) shows the evolution of $\bar{H}$ and S at different radial positions. We observe from figures 20(a) and 20(c) that, at any time, $\bar{H}$ and S decrease with the radial distance since the flow becomes slower near the edge. While $\bar{H}$ decreases monotonically with $\bar{r}$ similar to the case for steady flow, S exhibits a minimum close to the edge, which is not usually predicted or observed for steady flow. While $\bar{H}$ reaches the same constant level, S continues to grow with time, which is reflected in the curve corresponding to ${r_\infty }$ in figure 20(d). We observe from figures 20(b) and 20(d) that, for a given radial position, $\bar{H}$ and S increase with time during the acceleration period and overshoot their final steady states. The overshoot occurs at $\bar{t} \approx {\bar{t}_c}$ when the acceleration is halted. We recall from (3.23) that the pressure, downstream of the jump, is related to the film height, and therefore, the evolution of $\bar{H}$ in figure 20(b) reflects the evolution of the pressure. Consequently, figure 20(b) suggests that, similar to the transient behaviour of the pressure in the developing boundary-layer region (see figure 7), the pressure downstream of the jump also increases with time. However, no sudden changes occur before or after the acceleration period since the film height evolves smoothly with time. We also note that the pressure decreases with the radial distance in both the supercritical and subcritical regions. Finally, figure 20(b,c) shows that $\bar{H}$ and S reach their final steady state at $\bar{t} > {\bar{t}_c}$, suggesting that the long-term transient behaviour is not restricted to the supercritical region.

Figure 20. Transient behaviour of the subcritical film thickness and surface velocity for $A = 0.022$ and ${\bar{t}_c} = 50$. The profiles of $\bar{H}$ and S are plotted against the radial distance at equal time intervals (a,c), and against time at different radial positions (b,d). The curves $\bar{t} > 50$ in (a,c) correspond to the final steady-state profiles. The red curve represents the locus of the jump points whereas the green solid curve represents the locus of the final steady state reached by $\bar{H}$ and S at different $\bar{r}$. The jump is determined for $Re = 100$, $Fr = 10$, $We = 120$, ${\bar{H}_\infty } = 5.1$ and ${\bar{r}_\infty } = 5.38$.

We now explore the effect of gravity, which is found to have a significant influence on the transient response of the jump. Therefore, we consider varying Fr while keeping Re and We fixed. The base case corresponds to the values taken in the comparison with the numerical simulation earlier, namely $Re = 100$, $Fr = 10$ and $We = 120$. We also take ${\bar{H}_\infty } = 5.1$ and ${\bar{r}_\infty } = 5.38$. The influence of Fr on the transient response of the jump radius ${\bar{r}_J}(\bar{t})$, the upstream jump height ${\bar{h}_J}(\bar{t})$ and surface velocity ${s_J}(\bar{t})$, as well the downstream jump height ${\bar{H}_J}(\bar{t})$, is illustrated in figure 21. We also include the final steady state as the green solid curve. As expected, the jump radius increases with time as the jet is accelerated. For any Fr, ${\bar{r}_J}$ increases monotonically before reaching its final steady state (figure 21a). Similarly, the upstream and downstream jump heights also increase with time, but they overshoot their final steady-state level (see figure 21b,d) at a time close to $\bar{t} = {\bar{t}_c}$ (dashed vertical line) when the acceleration is halted. This behaviour is similar to that depicted in figure 21(b). The overshoot occurs later and intensifies further for a lower gravity level. We also observe that the overshoot in ${\bar{h}_J}$ and ${\bar{H}_J}$ is accompanied by a weak undershoot in ${s_J}$ (see figure 21c).

Figure 21. Influence of the Froude number (gravity) on the transient response of ${\bar{r}_J}$ (a), ${\bar{h}_J}$ (b), ${s_J}$ (c) and ${\bar{H}_J}$ (d) for $A = 0.022$, ${\bar{t}_c} = 50$, $Re = 100$, $We = 120$, ${\bar{H}_\infty } = 5.1$ and ${\bar{r}_\infty } = 5.38$. The green solid curve represents the locus of the final steady state reached by the different variables.

In the limit of small Fr, the flow responds almost instantly to the ending of the acceleration period, and ${\bar{r}_J}$, ${\bar{h}_J}$, ${s_J}$ and ${\bar{H}_J}$ reach their final steady state at $\bar{t} = {\bar{t}_c}$. However, as Fr increases, the final steady state is reached at $\bar{t} = {\bar{t}_c}$, and ${\bar{r}_J}$, ${\bar{h}_J}$ and ${\bar{H}_J}$ increase overall. Obviously, this is due to the effect of inertia carrying itself for longer times, especially when gravitational effects are weakened across the jump. Moreover, figure 21(a–d) shows that in the limit of high Fr, ${\bar{r}_J}$, ${\bar{h}_J}$, ${s_J}$ and ${\bar{H}_J}$ remain initially unchanged for a very short period before evolving with time, suggesting that, at low gravity, the jump response to the jet acceleration is initially delayed. Finally, it is interesting to observe that, while ${\bar{r}_J}$ and ${\bar{h}_J}$ deviate significantly from the initial steady state to reach a much higher steady-state level, ${s_J}$ and ${\bar{H}_J}$ tend to reach essentially the same level as the initial steady state.

As discussed earlier, when the gravitational effect is weak, the jump continues to slowly expand for some time as a result of its inertia. A similar behaviour was observed experimentally by Lamiel et al. (Reference Lamiel, Lamarque, Hélie and Legendre2021) in the evolution of a circular film induced by the impingement of a spray generated by a high-pressure injector on a horizontal plate. A spray was injected at a constant flow rate (constant injection pressure) for some period before the injection was stopped. It was shown that the circular film spreading on the plate wall continued to expand in the radial direction for some time after the injection had stopped (see their figure 5). Moreover, it was observed that increasing the injection pressure yielded a larger radius of the film at any time during the injection period and after the injection period (see their figure 10). This behaviour is similar to what is depicted in figure 21(a) in terms of the influence of Fr on the evolution of the jump radius during and after the acceleration period.