1. Introduction
The motion of elongated drops in vertical pipes arises in many engineering systems, such as buoyancy-driven displacements in wells and chemical reactors (Baird et al. Reference Baird, Aravamudan, Rao, Chadam and Peirce1992; Frigaard & Scherzer Reference Frigaard and Scherzer1998; Sahu & Vanka Reference Sahu and Vanka2011; Alba, Taghavi & Frigaard Reference Alba, Taghavi and Frigaard2014; Hasnain & Alba Reference Hasnain and Alba2017; Hasnain, Segura & Alba Reference Hasnain, Segura and Alba2017; Etrati & Frigaard Reference Etrati and Frigaard2018; Mirzaeian & Alba Reference Mirzaeian and Alba2018; Amiri et al. Reference Amiri, Eslami, Mollaabbasi, Larachi and Taghavi2019; Oladosu et al. Reference Oladosu, Hasnain, Brown, Frigaard and Alba2019). In nature, it is important for understanding conduit flow in persistently degassing volcanoes (Francis, Oppenheimer & Stevenson Reference Francis, Oppenheimer and Stevenson1993; Kazahaya, Shinohara & Saito Reference Kazahaya, Shinohara and Saito1994; Stevenson & Blake Reference Stevenson and Blake1998; Fowler & Robinson Reference Fowler and Robinson2018; Suckale et al. Reference Suckale, Qin, Picchi, Keller and Battiato2018). In all of these systems, gravity is the only driving force that generates the exchange flow of fluids with different densities.
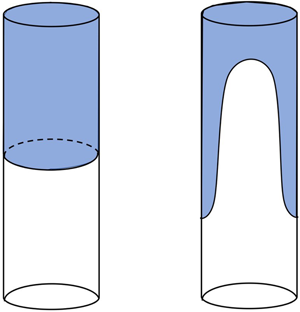
A typical experimental mechanism that leads to the formation of elongated drops is the lock-exchange configuration. In this set-up, a heavier fluid is initially separated from a lighter fluid by a horizontal barrier. Retraction of this barrier at the onset of the experiment releases the heavier fluid into the lighter fluid (see figure 1). The light fluid takes a symmetrical bullet shape, commonly called a Taylor drop, while the heavy fluid sinks as a film along the domain walls. Although an analytic description for the ascent speed of the drop may be useful for many problems, including the experimental study of slug flows (Joseph & Renardy Reference Joseph and Renardy1992; Brauner Reference Brauner1998), the dynamics of an isolated Taylor drop moving in a closed environment has not yet been quantified in detail.
Figure 1. Sketch of the lock-exchange problem in a vertical pipe of length 
$2L$ and radius 
$R$. At time 
$\hat {t}=0$, the top part of the pipe is filled with the heavier, descending fluid (dark blue) and the bottom part with the lighter, ascending fluid (white). When the lock is removed, a Taylor drop of length 
$\mathcal {L}$ and thickness 
$\hat {\delta }$ forms and the front ascends at speed 
$\hat {V}_f$ while the tail descends at speed 
$\hat {V}_t$.
Previous research has focused primarily on understanding the ascent dynamics of a gaseous Taylor bubble (Dumitrescu Reference Dumitrescu1943; Davies & Taylor Reference Davies and Taylor1950; White & Beardmore Reference White and Beardmore1962; Brown Reference Brown1965; Zukoski Reference Zukoski1966; Viana et al. Reference Viana, Pardo, Yanez, Trallero and Joseph2003). When capillary forces are negligible and inertial effects dominate over viscous forces, the Taylor bubble rises with a speed that is proportional to 
$\sqrt {gD}$. This result has been obtained theoretically by Dumitrescu (Reference Dumitrescu1943) and Davies & Taylor (Reference Davies and Taylor1950) using the potential flow theory for an ellipsoidal inviscid bubble and has later been confirmed by several experiments (White & Beardmore Reference White and Beardmore1962; Brown Reference Brown1965; Zukoski Reference Zukoski1966; Viana et al. Reference Viana, Pardo, Yanez, Trallero and Joseph2003). When viscous forces dominate over inertial and surface tension effects, the ascent speed of a gaseous Taylor bubble is proportional to 
${\rm \Delta} \rho g D^2/\mu _d$, where 
$\mu _d$ is the viscosity of the liquid (Brown Reference Brown1965; Wallis Reference Wallis1969). In contrast, when surface tension dominates over buoyancy, the ascent speed and film thickness are controlled by capillary forces (Bretherton Reference Bretherton1961; Reinelt Reference Reinelt1987; Batchelor Reference Batchelor2000; Llewellin et al. Reference Llewellin, Bello, Taddeucci, Scarlato and Lane2012; Shukla et al. Reference Shukla, Kofman, Balestra, Zhu and Gallaire2019).
Most existing studies assume a density contrast of multiple orders of magnitude between the Taylor bubble and the surrounding fluid. In some natural systems, however, the two overturning fluids have similar densities, leading to the formation of Taylor drops rather than Taylor bubbles. One specific example where this flow configuration arises is the conduit of a persistently active volcano (e.g. Francis et al. Reference Francis, Oppenheimer and Stevenson1993). Persistent activity is driven by degassing as evidenced by continual emissions of large quantities of gas, which are occasionally punctuated by the eruption of comparatively negligible quantities of magma (e.g. Vergniolle & Mangan Reference Vergniolle and Mangan2000). Originally dissolved in the magma, volatiles exsolve as the magma ascends, forming a large number of small bubbles. Most bubbles remain largely or partially entrained in the ambient flow due to the high magma viscosity. As a consequence, a Taylor drop of bubble-rich, buoyant magma can form and ascend to the surface where the bubbles escape, depriving the magma of its buoyancy and leaving it for recycling back to depth (e.g. Stevenson & Blake Reference Stevenson and Blake1998; Beckett et al. Reference Beckett, Mader, Phillips, Rust and Witham2011; Kerswell Reference Kerswell2011; Suckale et al. Reference Suckale, Qin, Picchi, Keller and Battiato2018). Since magma viscosity depends very sensitively on the dissolved volatile content and temperature, the viscosity between upwelling and downwelling magmas can vary by several orders of magnitude (Giordano, Russell & Dingwell Reference Giordano, Russell and Dingwell2008).
Up to now, only the experiments by Stevenson & Blake (Reference Stevenson and Blake1998) and Goldsmith & Mason (Reference Goldsmith and Mason1962) constrain the ascent dynamics of Taylor drops in a regime where viscous forces dominate over inertial and surface tension effects. While Goldsmith & Mason (Reference Goldsmith and Mason1962) investigated the motion of an isolated Taylor drop, Stevenson & Blake (Reference Stevenson and Blake1998) focused primarily on vertical lock-exchange systems for a large range of viscosity contrasts. Stevenson & Blake (Reference Stevenson and Blake1998) found that the non-dimensional rise speed of both isolated drops and elongated drops formed from a lock-exchange configuration saturates at a constant value when the viscosity of the surrounding fluid is approximately an order of magnitude higher than the viscosity of the drop. This finding has been confirmed by models (Suckale et al. Reference Suckale, Qin, Picchi, Keller and Battiato2018). Also, Kurimoto, Hayashi & Tomiyama (Reference Kurimoto, Hayashi and Tomiyama2013) and Hayashi, Kurimoto & Tomiyama (Reference Hayashi, Kurimoto and Tomiyama2011) measured the ascent speed of Taylor drops with and without the effect of surfactants when inertial forces are non-negligible. Direito, Campos & Miranda (Reference Direito, Campos and Miranda2016) showed numerically that the recirculation patterns inside a Taylor drop change significantly with the viscosity ratio.
The goal of this paper is to quantify the ascent dynamics of a Taylor drop confined in a vertical pipe when surface tension and inertia are negligible. We propose a theoretical framework that quantifies the interplay between buoyancy and viscous forces for an elongated Taylor drop. Our analytical model estimates the ascent speed and drop thickness from first principles and elucidates the effect of the viscosity ratio on the ascent dynamics of a Taylor drop. While our model is motivated primarily by the flow conditions arising in the conduits of persistently active volcanoes, as reflected in the non-dimensional regime we explore, it is generally applicable to Taylor drops in other fields of application.
We derive a lubrication model for a Taylor drop formed from a lock-exchange configuration and obtain the scaling of the ascent speed as a function of the drop thickness and the viscosity ratio (§ 2). The lubrication model solves for the velocity profiles in the drop and the surrounding fluid. To identify which configurations are stable, we analyse the energy balance of the whole system. We show that the drop obeys an ordinary differential equation for the drop thickness. The steady state is determined by the interplay of the potential energy and the viscous dissipation produced by the motion of the flowing fluids (§ 3). When the drop reaches its terminal ascent speed, its thickness is independent of the viscosity ratio in the non-dissipative regime (§ 4.1).
Our theory provides a new theoretical framework that not only explains the lock-exchange experiments of Stevenson & Blake (Reference Stevenson and Blake1998) (§ 4.2), but that can also be generalized to the case of an isolated elongated drop released into a vertical pipe (§ 4.3). Our theory agrees well with the measurements of Goldsmith & Mason (Reference Goldsmith and Mason1962) and provides new physical insights into the backflow patterns in Taylor drops in the presence of large variations in the viscosity contrast (§ 4.4).
2. Lubrication model
2.1. Governing equations
In the lock-exchange configuration, the fluids are initially unstably stratified. An elongated Taylor drop forms after lock removal, as sketched in figure 1. Assuming immiscible flow of two Newtonian fluids, the governing equations are continuity and Navier–Stokes in both fluids
\begin{gather} \boldsymbol{\nabla} \boldsymbol{\cdot} \hat{\boldsymbol{u}}_i=0, \end{gather}
\begin{gather}\rho_i \left[ \frac{\partial \hat{\boldsymbol{u}}_i}{\partial \hat{t}} + \left( \hat{\boldsymbol{u}}_i \boldsymbol{\cdot} \boldsymbol{\nabla} \right)\hat{\boldsymbol{u}}_i \right]= - \boldsymbol{\nabla} \hat{p}+\mu_i \nabla^2 \hat{\boldsymbol{u}}_i - \rho_i{g} \boldsymbol{e}_g, \end{gather}
where 
$\hat {p}$ is the pressure and 
$\hat {\boldsymbol {u}}=(\hat {v},\hat {w},\hat {u})$ is the velocity vector with 
$\hat {v}$, 
$\hat {w}$ and 
$\hat {u}$ representing the velocity components in the 
$r$, 
$\theta$ and 
$z$ directions, respectively. The subscripts, 
$i=d,a$, refer to the descending and ascending fluid, respectively. The dynamic viscosity and density of the fluids are 
$\mu _i$ and 
$\rho _i$. The acceleration due to gravity is denoted by 
$g$ and acts in the direction of unit vector 
$\boldsymbol {e}_g$. The boundary conditions are no-slip and no-penetration at the pipe wall and continuity of velocity and shear stresses at the fluid–fluid interface. In addition, the system satisfies the exchange-flow condition, which requires that the net volumetric flux is zero in each cross-section 
$\hat {A}$, i.e.
\begin{equation} \int_{\hat{A}_d} \hat{\boldsymbol{u}}_d \boldsymbol{\cdot} \boldsymbol{n}\,\textrm{d}\hat{S}+ \int_{\hat{A}_a} \hat{\boldsymbol{u}}_a\boldsymbol{\cdot} \boldsymbol{n} \,\textrm{d}\hat{S}={0}, \end{equation}
where 
$\boldsymbol {n}$ is the vector normal to the pipe cross-section. The dimensional parameters governing the flow are listed in table 1.
Table 1. List of the dimensional input parameters and variables of the problem.
2.2. Dimensionless formulation and lubrication approximation
In this section, we derive a lubrication model for a Taylor drop of length 
$\mathcal {L}$ and thickness 
$\hat {\delta }$. We assume that the drop is sufficiently long such that the fluid–fluid interface is approximately parallel to the vertical direction, 
$\hat {z}$ in figure 1. We can thus neglect the velocity component in the azimuthal direction, 
$\hat {w}_i=0$, which leaves 
$\hat {\boldsymbol {u}}_i=(\hat {v}_i,0,\hat {u}_i)$. The two relevant length scales in the vertical and radial directions are the length of the drop, 
$\mathcal {L}$, and the pipe radius 
$R$. Based on these, we define the scale parameter,
\begin{equation} \varepsilon=\frac{R}{\mathcal{L}}. \end{equation}
The identification of the velocity scale is not trivial since the volumetric flux cannot be predicted a priori. The spreading of the drop in the axial direction is controlled by a balance between buoyancy and viscous stress. Buoyancy is the driving force and it scales as 
${\rm \Delta} \rho g R$, where 
${\rm \Delta} \rho =\rho _d-\rho _a$ is the density difference between the ascending and the descending fluid. The stress at the wall dissipates the energy and it scales as 
$\mu _d U/R$. By matching the two contributions, we obtain the scale for the axial velocity component
\begin{equation} {\rm \Delta} \rho g R \sim \frac{\mu_dU}{R}\quad \Rightarrow \quad U=\frac{{\rm \Delta} \rho g R^2}{\mu_d}. \end{equation}
Using the continuity equations, we infer the characteristic scale of the radial component of the velocity as 
$\varepsilon U$.
We then normalize (2.1) by introducing the following dimensionless variables:
\begin{equation} {z}=\frac{\hat{{z}}}{\mathcal{L}}, \quad {r}=\frac{\hat{{r}}}{R}, \quad {t}=\frac{\hat{{t}}}{\mathcal{L}/U},\quad {u}_i=\frac{\hat{{u}}_i}{U}, \quad {v_i}=\frac{\hat{{v}}_i}{\varepsilon U}, \quad {p_i}=\frac{\hat{{p}}_i}{\mu_d U \mathcal{L} /R^2}. \end{equation}We obtain two momentum equations in the axial and radial directions for the descending fluid
\begin{gather} \varepsilon Ar\frac{\textrm{D} u_d}{\textrm{D} t}= -\frac{\partial {p_d}}{\partial {z}}+ \varepsilon \frac{\partial ^2 u_d}{ \partial {z}^2}+ \frac{1}{r}\frac{\partial }{\partial r } \left( r\frac{\partial {u}_d}{ \partial {r}} \right)-\frac{1}{1-\mathcal{R}}, \end{gather}
\begin{gather}\varepsilon^2 Ar\frac{\textrm{D} v_d}{\textrm{D} t}= -\frac{1}{\varepsilon}\frac{\partial {p_d}}{\partial {r}}+ \varepsilon^3 \frac{\partial ^2 v_d}{ \partial {z}^2}+ \varepsilon \left[ \frac{1}{r} \frac{\partial}{\partial r} \left( r \frac{\partial {v}_d}{ \partial {r}}\right)-\frac{v_d}{r^2} \right], \end{gather}and for the ascending fluid
\begin{gather} \varepsilon \mathcal{R}Ar\frac{\textrm{D} u_a}{\textrm{D} t}= -\frac{\partial {p_a}}{\partial {z}}+ \frac{\varepsilon}{M} \frac{\partial ^2 u_a}{ \partial {z}^2}+ \frac{1}{ M r} \frac{\partial }{\partial r } \left( r\frac{\partial {u}_a}{ \partial {r}} \right)-\frac{\mathcal{R}}{1-\mathcal{R}}, \end{gather}
\begin{gather}\varepsilon^2 \mathcal{R}Ar \frac{\textrm{D} v_a}{\textrm{D} t}= -\frac{1}{\varepsilon}\frac{\partial {p_a}}{\partial {r}}+ \frac{\varepsilon^3}{M} \frac{\partial ^2 v_a}{ \partial {z}^2}+ \frac{\varepsilon}{M} \left[ \frac{1}{r} \frac{\partial}{\partial r} \left( r \frac{\partial {v}_a}{ \partial {r}}\right)-\frac{v_a}{r^2}\right], \end{gather}where
\begin{equation} \frac{\textrm{D}}{\textrm{D} t}=\frac{\partial }{\partial {t}} + v_i\frac{\partial }{\partial {r}}+u_i\frac{\partial }{\partial {z}}, \end{equation}and
\begin{equation} Ar=\frac{\rho_d {\rm \Delta} \rho g R^3}{\mu_d^2},\quad \mathcal{R}=\frac{\rho_a}{\rho_d}, \quad M=\frac{\mu_d}{\mu_a}, \end{equation}
are the Archimedes number, 
$Ar$, the density ratio, 
$\mathcal {R}$, and the viscosity ratio, 
$M$, respectively. The Archimedes number represents the ratio between buoyancy and viscous forces. It is equivalent to the Reynolds number defined on our characteristic axial velocity scale 
$U$, since 
$Ar=Re_U=\rho _d U R/\mu _d$. The dimensionless parameters and variables of the problem are listed in table 2.
Table 2. List of the dimensionless parameters and variables of the problem.
In our analysis, we assume an elongated Taylor drop, i.e. 
$\varepsilon \ll 1$, with a region of constant drop thickness that extends over most of the length 
$\mathcal {L}$. In this limit, the axial derivative of 
$u_i$ and the terms including the radial component of the velocity 
$v_i$ can be neglected from (2.6) and (2.7), provided that 
$M\gg \varepsilon$. Therefore, (2.6) and (2.7) reduce to a one-dimensional set of equations
\begin{gather} \frac{1}{r}\frac{\textrm{d}}{\textrm{d} r} \left( r \frac{\textrm{d} u_d}{\textrm{d} r} \right)= \frac{\textrm{d} p}{\textrm{d} z}+\frac{1}{1-\mathcal{R}}, \quad r \in [\delta,1], \end{gather}
\begin{gather}\frac{1}{{{M}}} \frac{1}{ r}\frac{\textrm{d}}{\textrm{d} r} \left( r \frac{\textrm{d} u_a}{\textrm{d} r} \right)=\frac{\textrm{d} p}{\textrm{d} z}+\frac{\mathcal{R}}{1-\mathcal{R}},\quad r \in [0,\delta], \end{gather}
where 
$\partial p_i / \partial r=0$. Both fluids share the same pressure gradient, 
$\textrm {d} p_d/\textrm {d} z=\textrm {d} p_a/\textrm {d} z=\textrm {d} p/\textrm {d} z$. Since the normal stress at the fluid–fluid interface is continuous, we find that the pressure difference between the fluids is controlled by the Bond number, 
$Bo$, as follows:
\begin{equation} p_d-p_a=\frac{1}{\delta}\frac{\varepsilon}{Bo},\quad \textrm{with}\ Bo=\frac{{\rm \Delta} \rho g R^2}{{\sigma}}, \end{equation}
where 
$\sigma$ is the surface tension and 
$\delta =\hat {\delta }/R$ is the dimensionless drop thickness.
For elongated drops, the lubrication model (2.10) holds because the nonlinear terms on the left-hand side of (2.6) and (2.7) vanish. The model applies even at finite 
$Ar$ if the viscous scaling chosen for defining the velocity scale 
$U$ remains representative of the physics of the problem. We only consider cases where the descending fluid is heavier compared with the ascending fluid, 
$\rho _d>\rho _a$, and, therefore, 
$\mathcal {R}<1$. This choice is motivated by the problem of buoyancy-driven conduit flow in persistently degassing volcanoes and slug flow in vertical conduits more generally.
2.3. Velocity profiles and front speed
In this section, we derive analytical expressions for the velocity profiles, as well as for the ascent and descent speeds of the Taylor drop (illustrated in figure 2). After the release of the lock, the fluids start moving due to buoyancy: the lighter fluid penetrates into the heavier fluid at speed 
$V_f$ while the heavier fluid displaces the lighter fluid at speed 
$V_t$. Using a lubrication approximation, we conceptualize the Taylor drop as a region of core-annular flow with uniform thickness 
$\delta$ and length 
$|h_f|+|h_t|$, as sketched in figure 2.
Figure 2. View of the axial cross-section of the lock-exchange problem in a vertical pipe (
$z$–
$r$ plane) in dimensionless coordinates. The ascending front (red); the descending tail (green); the gain of potential energy area (green diagonal stripes); and the loss of potential energy (red diagonal stripes).
We integrate (2.10a) and (2.10b) subject to the following conditions.
(i) The pipe wall is no-slip and the radial derivative of velocity is zero at the pipe centre,
(2.12a,b)
\begin{equation} u_d(1)=0,\quad \frac{\textrm{d}}{\textrm{d} r}u_a(0)=0. \end{equation}(ii) Velocity and shear stress are continuous at the fluid–fluid interface,
(2.13a,b)\begin{equation} u_d(\delta)=u_a(\delta),\quad \frac{\textrm{d}}{\textrm{d} r}u_d(\delta)=\frac{1}{M} \frac{\textrm{d}}{\textrm{d} r}u_a(\delta). \end{equation}
We obtain the velocity profiles
\begin{gather} u_d(r)=\frac{P}{4} \left(r^2-1\right)-\frac{{\delta}^2}{2} \log r,\quad r \in [\delta,1], \end{gather}
\begin{gather}u_a(r)={{M}}\frac{P-1}{4 }\left( r^2-{\delta}^2\right)+ \frac{P}{4}\left({\delta}^2-1\right)- \frac{{\delta}^2}{2} \log \delta,\quad r \in [0,\delta], \end{gather}
where 
$P=\textrm {d} p/\textrm {d} z+1/(1-\mathcal {R})$ is the dimensionless driving force of the ascending fluid. We can eliminate the pressure gradient from (2.14a) and (2.14b) using the exchange-flow condition (2.2),
\begin{equation} \int_{\delta}^1 2 {\rm \pi}r u_d \,\textrm{d} r + \int_0^{\delta} 2 {\rm \pi}r u_a \,\textrm{d} r=0, \end{equation}
and find that 
$P$ is a function of the drop thickness and the viscosity ratio
\begin{equation} P= {\delta}^2 \frac{2 {({\delta}^2-1)}- {{M}}{\delta}^2 }{{\delta}^4-1-{{M}}{\delta}^4}. \end{equation}
This relation clarifies how the vertical pressure gradient 
$\textrm {d} p/\textrm {d} z$ changes with 
$\delta$, 
$M$ and 
$\mathcal {R}$ under exchange-flow condition, see figure 3. As expected, the magnitude of the driving force increases with the density difference between the fluids, see figure 3(b).
Figure 3. (a) Dimensionless pressure gradient 
$\textrm {d} p/\textrm {d} z$ as a function of the drop thickness 
$\delta$ and the viscosity ratio 
$M$ for 
$\mathcal {R}=0.8$. (b) Dimensionless pressure gradient as a function of the drop thickness 
$\delta$ and the density ratio 
$\mathcal {R}$ for 
$M=1$.
When the drop thickness vanishes for 
$\delta \rightarrow 0$, the pressure gradient approaches the single-phase limit balancing the gravitational force of the descending fluid, 
$\textrm {d} p/\textrm {d} z \rightarrow -1/(1-\mathcal {R})$. In the opposing limit of 
$\delta \rightarrow 1$, 
$\textrm {d} p/\textrm {d} z$ balances the gravitational force of the ascending fluid.
We obtain the ascent and descent speeds by integrating the velocity profiles
\begin{equation} V_f=\frac{1}{{\rm \pi} \delta^2}\int^{\delta}_0 2 {\rm \pi}r u_a \,\textrm{d} r\quad \textrm{and}\quad V_t=\frac{1}{{\rm \pi} (1-\delta^2)}\int_{\delta}^1 2 {\rm \pi}r u_d \,\textrm{d} r, \end{equation}yielding
\begin{gather} V_f= -\frac{\delta^2}{8}\frac{ 4[1+(M-1)\delta^4]\log \delta + (4-3M)\delta^4 +4(M-2)\delta^2-M+4 }{1+(M-1)\delta^4}, \end{gather}
\begin{gather}V_t= -\frac{\delta^4}{8}\frac{ 4[1+(M-1)\delta^4]\log \delta + (4-3M)\delta^4 +4(M-2)\delta^2-M+4 }{(M\delta^4-\delta^4+1)(\delta^2-1)}. \end{gather}
The estimated speeds, 
$V_f$ and 
$V_t$, are functions of the drop thickness and the viscosity ratio only as plotted in figure 4. The two curves quantify how much 
$V_f$ and 
$V_t$ change with 
$\delta$ while satisfying the exchange-flow condition. The two speeds are related through (2.15) as
\begin{equation} A_aV_f +A_dV_t=0, \end{equation}where
\begin{equation} A_a={\rm \pi} \delta^2,\quad A_d={\rm \pi}(1-\delta^2), \end{equation}are the dimensionless cross-sectional area of the ascending and the descending fluids, respectively. Therefore, the two speeds and areas satisfy the following relation:
\begin{equation} \frac{V_t}{V_f}=-\frac{A_a}{A_d}=-\frac{\delta^2}{1-\delta^2}. \end{equation}
The ascent speed is maximal for 
$M\rightarrow \infty$. In this limit, the viscosity of the descending fluid greatly exceeds that of the ascending fluid. As a consequence, the fluid–fluid interface resembles a free surface as evident when applying the limit 
$M\rightarrow \infty$ to the interface condition (2.13a,b) 
$\textrm {d} u_d/\textrm {d} r|_\delta \approx 0$. We refer to this case as the free-surface limit, where the asymptotic speeds are
\begin{gather} V_f\left( \delta, M\rightarrow \infty \right)=\frac{\delta^4(1-\log{\delta})+1-4\delta^2}{8\delta^2}, \end{gather}
\begin{gather}V_t\left( \delta, M\rightarrow \infty \right)=\frac{\delta^4(3-4\log{\delta})+1-4\delta^2}{8(\delta^2-1)}. \end{gather}
The other asymptotic limit is 
$M \rightarrow 0$. In this case, the drop is so viscous that it can be approximated as a rigid body. We refer to this limit as the rigid-core limit, which is characterized by
\begin{gather} V_f\left( \delta, M\rightarrow 0 \right)=-\frac{\delta^2(1-\delta^2+\log{\delta}+\delta^2 \log{\delta})}{2(\delta^2+1)}, \end{gather}
\begin{gather}V_t\left( \delta, M\rightarrow 0 \right)=\frac{\delta^4( 1+\log{\delta} - \delta^2 -\delta^2 \log{\delta} )}{2(\delta^4-1)}. \end{gather}3. Energy analysis
3.1. Energy balance
Here, we formulate the energy balance for the Taylor drop formed from a lock-exchange configuration as conceptualized in figure 2. Our analysis applies once the Taylor drop has formed and elongated sufficiently such that the lubrication approximation derived in § 2 holds. We do not consider transient behaviour immediately after the release of the lock.
We start from the energy balance formulated by Dussan (Reference Dussan1975) for a closed system filled with two immiscible fluids that occupy the volume 
$\hat {\mathcal {V}}=\hat {\mathcal {V}}_a \cup \hat {\mathcal {V}}_d$ and are separated by the fluid–fluid interface 
$\hat {\varSigma }$ given by
\begin{equation} \frac{\textrm{d} }{\textrm{d} \hat{t}}\left[ \hat{\mathcal{E}}+\hat{\mathcal{P}}+\oint_{\hat{\varSigma}} \sigma\,\textrm{d}\hat{S}\right]=\oint_{\partial \hat{\varSigma}} \sigma {\boldsymbol{t}} \boldsymbol{\cdot} \hat{\boldsymbol{U}}\,\textrm{d}\hat{\ell} + \int_{\partial \hat{\mathcal{V}}} \hat{\boldsymbol{u}} \boldsymbol{\cdot} \left(\hat{\boldsymbol{\tau}} \boldsymbol{\cdot} {\boldsymbol{n}}\right) \textrm{d}\hat{S}-\hat{\varPhi}, \end{equation}
where 
$\hat {\mathcal {E}}$, 
$\hat {\mathcal {P}}$, 
$\oint _{\hat {\varSigma }} \sigma \,\textrm {d}\hat {S}$ and 
$\hat {\varPhi }$ are the kinetic, the potential, the surface energy and the total viscous dissipation of the system, respectively, while 
$\hat {\boldsymbol {U}}$, 
$\hat {\boldsymbol {\tau }}$ and 
$\boldsymbol {t}$ are the velocity of the contact line, the shear stress tensor and the unit vector normal to 
$\partial \hat {\varSigma }$ on 
$\hat {\varSigma }$. The first integral on the right-hand side of (3.1) accounts for the work done by the contact line 
$\partial \hat {\varSigma }$. The second integral is the work of the traction on the pipe wall 
$\partial \hat {\mathcal {V}}$, which is zero in our case since the motion is not forced from the boundary (Joseph, Nguyen & Beavers Reference Joseph, Nguyen and Beavers1984). The last term is the viscous dissipation produced in the whole fluid domain.
If we non-dimensionalize (3.1) based on the characteristic scales defined in (2.5a–f), we obtain
\begin{equation} \frac{\textrm{d}}{\textrm{d} t}\left[\frac{1}{Ri}\mathcal{E}+\mathcal{P}+(1-\mathcal{R}) \frac{\varepsilon}{Bo}\oint_{\varSigma} \textrm{d} S\right]= (1-\mathcal{R})\frac{\varepsilon}{Bo} \oint_{\partial \varSigma} \boldsymbol{t} \boldsymbol{\cdot} \boldsymbol{U}\,\textrm{d}\ell - (1-\mathcal{R})\varPhi, \end{equation}
where 
$Ri$ is the Richardson number of the Taylor drop defined as
\begin{equation} Ri=\frac{g\mathcal{L}}{U^2}. \end{equation}
The Richardson number represents the ratio between potential energy, 
$\rho _a g \mathcal {L}$, and kinetic energy, 
$\rho _a U^2$. As described in § 2.2, we are interested in elongated drops, 
$\varepsilon \ll 1$, and, therefore, we can eliminate the surface energy and the work of the contact line terms from (3.2). With this, we obtain a simplified energy balance
\begin{equation} \frac{\textrm{d} }{\textrm{d} t}\left[\frac{1}{Ri} \mathcal{E}+\mathcal{P}\right]= -(1-\mathcal{R})\varPhi, \end{equation}
where energy of the system is approximated by the sum of the kinetic and potential energy and is dissipated only through viscous dissipation. This simplification holds in systems with negligible surface tension, 
$Bo\gg \varepsilon$.
Based on the scaling chosen in this paper, see (2.5a–f), we can rewrite 
$Ri$ as
\begin{equation} Ri= \frac{1}{(1-\mathcal{R})\varepsilon Ar}, \end{equation}
and further simplify the energy balance in the limit of 
$Ri\rightarrow \infty$ as
\begin{equation} \frac{\textrm{d}}{\textrm{d} t}\mathcal{P}= -(1-\mathcal{R})\varPhi. \end{equation}In this case, the dynamics of the system is controlled by the interplay between the time rate of potential energy and viscous dissipation.
3.1.1. Kinetic energy
The kinetic energy of the system is defined as
\begin{equation} \hat{\mathcal{E}}= \int_{\hat{\mathcal{V}}_d} \tfrac{1}{2} \rho_d \hat{u}_d^2 \,\textrm{d}\hat{{V}}+ \int_{\hat{\mathcal{V}}_a} \tfrac{1}{2} \rho_a \hat{u}_a^2 \,\textrm{d}\hat{{V}}. \end{equation}
We only consider the kinetic energy in the drop region 
$\mathcal {L}$ where the analytical velocity profiles (2.14) apply. We neglect the kinetic energy in the region above and below the Taylor drop because the aspect ratio of the pipe is very small, 
$R/L\ll 1$. This simplification is equivalent to assuming that the regions of pure fluids above and below the drop act as infinite reservoirs. Using (2.14) in (3.7) and integrating over the region 
$\mathcal {L}$ of constant thickness 
$\delta$, we obtain the dimensionless kinetic energy
\begin{equation} \mathcal{E}= {\rm \pi}(h_f-h_t) \left[ \frac{1}{1-\mathcal{R}} \int_\delta ^1 r u_d^2 \,\textrm{d} r+ \frac{\mathcal{R}}{1-\mathcal{R}} \int^\delta _0 r u_a^2\,\textrm{d} r \right], \end{equation}where we express the height of the ascending front and the descending tail as
\begin{equation} h_f={V}_f {t} \quad \textrm{and}\quad {h}_t={V}_t {t}. \end{equation}Finally, we obtain
\begin{align} \mathcal{E} &= {\rm \pi}\frac{(V_f-V_t)t}{96 } \left[ \left(\frac{1}{\mathcal{R}-1}-\delta^6-3\delta^4-3\delta^2 \right)P^2 +12(\log\delta)^2 \left( \delta^6 + \frac{\delta^4}{\mathcal{R}-1}\right) \right. \nonumber\\ &\quad \left. -6\delta^2P\log\delta \left( \delta^4-2\delta^2 -\frac{1}{\mathcal{R}-1}\right) \right]. \end{align}3.1.2. Potential energy
The potential energy of the system at the time 
$\hat {t}$ is defined as
\begin{equation} \hat{\mathcal{P}}= \int_{\hat{\mathcal{V}}_d} \rho_d g \hat{z}_d \,\textrm{d}\hat{{V}}+ \int_{\hat{\mathcal{V}}_a} \rho_a g \hat{z}_a \,\textrm{d}\hat{{V}}. \end{equation}
Since we assume constant thickness 
$\hat {\delta }$, (3.11) becomes
\begin{equation} \hat{\mathcal{P}}= \rho_d g \left[\hat{A}_d \int_{\hat{h}_t}^{\hat{h}_f} \hat{z}_d \,\textrm{d}\hat{z}+ \hat{A}\int^{L}_{\hat{h}_f} \hat{z}_d \,\textrm{d}\hat{z}\right] + \rho_a g \left[\hat{A}_a\int_{\hat{h}_t}^{\hat{h}_f} \hat{z}_a \,\textrm{d}\hat{z}+\hat{A} \int^{\hat{h}_t}_{-L} \hat{z}_d \,\textrm{d}\hat{z} \right], \end{equation}and we obtain
\begin{equation} \hat{\mathcal{P}}= \tfrac{1}{2}g \hat{A}_d \hat{h}_t^2 (\rho_d-\rho_a) -\tfrac{1}{2}g \hat{A}_a \hat{h}_f^2 (\rho_d-\rho_a)+ \tfrac{1}{2}(\rho_d-\rho_a)g\hat{A}L^2, \end{equation}
where 
$\hat {A}={\rm \pi} R^2$, 
$\hat {A}_a={\rm \pi} \hat {\delta }^2$ and 
$\hat {A}_d={\rm \pi} (R^2- \hat {\delta }^2)$ are the pipe cross-section and the cross-sectional areas occupied by the ascending and the descending fluids, respectively. Using (3.9a,b) and recasting the equation in terms of dimensionless variables, yields
\begin{equation} {\mathcal{P}}= \frac{1}{2} \left( A_d V_t^2 - A_a V_f^2\right)t^2 + \frac{\rm \pi}{2} L^2 _*, \end{equation}
where the dimensionless areas 
$A_a$ and 
$A_d$ are defined in (2.21a,b) and 
$L_*=L/{\rm \Delta} \rho g U^2 R^2$ is a constant.
Before the removal of the lock at time 
$t=0$, the velocity field is zero everywhere and the potential energy is maximal, see figure 2. Between the time instants 
$t$ and 
$t+\textrm {d} t$, the light fluid invades a region 
$\textrm {d}\mathcal {V}_f$ that was previously occupied by the heavy fluid. Although the potential energy of the ascending fluid increases due to the increased height of the column, the replacement of the heavy fluid by the light fluid results in a loss of 
$\mathcal {P}$. At the descending tail, instead, the heavy fluid occupies a region 
$\textrm {d}\mathcal {V}_t$ that was previously occupied by the lighter fluid, resulting in a gain of 
$\mathcal {P}$. These two competing mechanisms are evident when examining the time derivative of the potential energy (keeping 
$\delta$ fixed)
\begin{equation} \left(\frac{\partial \mathcal{P}}{\partial t}\right)_\delta= ( \underbrace{A_d V_t^2}_{{gain}} \underbrace{- A_a V_f^2}_{{loss}} )t. \end{equation}
The rate at which 
$\mathcal {P}$ increases scales with 
$A_dV_t^2$ while the rate of energy loss scales with 
$A_aV_f^2$.
3.1.3. Viscous dissipation
We only consider the viscous dissipation in the region 
$\mathcal {L}$. Viscous dissipation is defined as
\begin{equation} \hat{\varPhi}= \int_{\hat{\mathcal{V}}_d} \mu_d \left(\frac{\partial \hat{u}_d}{\partial \hat{r}}\right)^2 \textrm{d}\hat{V}+ \int_{\hat{\mathcal{V}}_a} \mu_a \left(\frac{\partial \hat{u}_a}{\partial \hat{r}}\right)^2 \textrm{d}\hat{V}, \end{equation}or, in term of dimensionless variables,
\begin{equation} \varPhi=(h_f-h_t)\left[\int_{\delta}^1 2 {\rm \pi}r \left(\frac{\textrm{d} u_d}{\textrm{d} r}\right)^2 \textrm{d} r + \frac{1}{M}\int _0^{\delta} 2 {\rm \pi}r \left(\frac{\textrm{d} u_a}{\textrm{d} r}\right)^2 \textrm{d} r\right]. \end{equation}After using the velocity profiles from (2.14) and our estimates for front and tail heights (3.9a,b), we obtain
\begin{equation} \varPhi= 2 {\rm \pi}(V_f-V_t) \left[ \frac{P}{16}({\delta}^2-1)^2+ \frac{{\delta}^2}{8} ({\delta}^2-1-2{\delta}^2\log {\delta})\right]t. \end{equation}We can further simplify (3.18) using (2.18), (2.19) and (2.22) yielding
\begin{equation} \varPhi= A_aV_f(V_f-V_t) t. \end{equation}3.2. Time evolution of the drop thickness
We now use the energy balance (3.4) to track the evolution of the drop thickness over time 
$\delta (t)$. We start by observing that the kinetic and potential energy, (3.10) and (3.14), and the viscous dissipation (3.18), depend only on the drop thickness 
$\delta$, the time 
$t$ and a finite number of material parameters including the viscosity and density ratios and the Richardson number. Therefore, we can recast the energy balance as follows:
\begin{equation} \left[ \frac{1}{Ri} \frac{\partial \mathcal{E}}{\partial \delta} + \frac{\partial \mathcal{P}}{\partial \delta} \right] \frac{\textrm{d} \delta}{\textrm{d} t} + \frac{1}{Ri}\frac{\partial \mathcal{E}}{\partial t} +\frac{\partial \mathcal{P}}{\partial t}= -(1-\mathcal{R})\varPhi . \end{equation}
Since all the derivatives of the kinetic and potential energy (
$\partial /\partial \delta$ and 
$\partial /\partial t$) can be computed analytically, (3.20) is an ordinary differential equation for 
$\delta (t)$ in the form
\begin{equation} f(\delta,t) \frac{\textrm{d} \delta}{\textrm{d} t} + g(\delta,t)= -(1-\mathcal{R})\varPhi(\delta,t), \end{equation}where
\begin{gather} f(\delta,t)=\frac{1}{Ri} \frac{\partial \mathcal{E}}{\partial \delta} + \frac{\partial \mathcal{P}}{\partial \delta}, \end{gather}
\begin{gather}g(\delta,t)=\frac{1}{Ri}\frac{\partial \mathcal{E}}{\partial t} +\frac{\partial \mathcal{P}}{\partial t}. \end{gather}
The analytical expression for 
$g(\delta ,t)$ and the computational procedure for 
$f(\delta ,t)$ are detailed in appendix A. Equation (3.21) can then be solved for any initial condition in the domain 
$\delta \in [0,1]$ for 
$t \in [t_0,\infty ]$.
When 
$Ri \rightarrow \infty$ we can simplify (3.21) to
\begin{equation} \frac{\partial \mathcal{P}}{\partial \delta} \frac{\textrm{d} \delta}{\textrm{d} t} + \frac{\partial \mathcal{P}}{\partial t}= -(1-\mathcal{R})\varPhi . \end{equation}
The full analytical expressions are reported in appendix B. For sake of physical interpretation, we focus on three end-member cases when solving (3.24) while distinguishing between the non-dissipative (
$\varPhi =0$) and the dissipative regimes (
$\varPhi \neq\,0$):
(i) two isoviscous fluids,
$M=1$,
(3.25)\begin{equation} \frac{\textrm{d} \delta}{\textrm{d} t} = -\frac{\delta (\delta^2-1)(2\delta^2-\psi) (\delta^4-4\delta^4+4\log \delta +3)}{t[ (24\delta^4-40\delta^2+12)\log \delta 14 \delta^8 -62 \delta^6 +97 \delta^4 -62 \delta^2 +13]}; \end{equation}(ii) the rigid-core limit,
$M\rightarrow 0$,
(3.26)\begin{align} \frac{\textrm{d} \delta}{\textrm{d} t} = -\frac{\delta (\delta^4-1)(2\delta^2-\psi)[(\delta^2+1) \log {\delta}-\delta^2+1]}{t [ (\delta^2+1)^2(6\delta^4-10\delta^2+3)\log \delta -4\delta^8 +3\delta^6 +12\delta^4-15\delta^2+4 ]}; \end{align}(iii) the free-surface limit,
$M\rightarrow \infty$,
(3.27)\begin{equation} \frac{\textrm{d} \delta}{\textrm{d} t} = -\frac{\delta (\delta^2-1)(2\delta^2-\psi)(4\delta^4\log {\delta}-3\delta^4+4\delta^2-1)}{t[ (24\delta^8-40\delta^6+12\delta^4)\log \delta -10 \delta^8 +26 \delta^6 -19 \delta^4 +2 \delta^2 +1] }, \end{equation}
where
\begin{gather} \psi=1 \quad \textrm{when}\ {\varPhi}=0, \end{gather}
\begin{gather}\psi=\mathcal{R} \quad \textrm{when}\ {\varPhi}\neq 0 . \end{gather}
Note that (3.25), (3.26) and (3.27) have been obtained taking the asymptotic limits of (B 2) for 
$M\rightarrow 1$, 
$M\rightarrow 0$ and 
$M\rightarrow \infty$, respectively. In the absence of dissipation, we can compute the steady-state solutions of (3.25), (3.26) and (3.27) in the range 
$\delta \in [0,1]$ by computing the roots of 
$\textrm {d}\delta /\textrm {d} t=0$. We obtain three steady-state solutions
\begin{equation} \delta_\infty= \frac{\sqrt{2}}{2},\quad \delta_\infty= 0\quad \mbox{and} \quad \delta_\infty= 1 . \end{equation}Equivalently, in the dissipative regime, the three steady-state solutions are
\begin{equation} \delta_\infty= \frac{\sqrt{2\mathcal{R}}}{2}, \quad \delta_\infty= 0 \quad \mbox{or} \quad \delta_\infty= 1. \end{equation}4. Discussion
4.1. Transient evolution and ascent speed of the Taylor drop
We obtain the transient evolution of the Taylor drop by solving the ordinary differential equation (3.21) in time for an arbitrary initial condition. We initialize the problem with a drop of thickness 
$\delta \in [0,1]$ and compute the time evolution in the interval 
$[t_0,\infty ]$. The computations are performed using the stiff solver ode15s of Matlab. The ordinary differential equation (3.21) is singular at 
$t=0$, because the model only applies once a Taylor drop has formed. We hence start our computation at 
$t_0=10$ to guarantee the uniqueness of the solution for arbitrary initial drop thickness, viscosity ratio and Richardson number. We focus on Richardson numbers in the range 
$Ri \in [1, \infty ]$ and present the time evolution of 
$\delta (t)$ for (i) the rigid-core limit, (ii) isoviscous fluids and (iii) the free-surface limit.
In the non-dissipative regime, the drop thickness converges to the stable solution 
$\delta _{\infty }=\sqrt {2}/2$ for an intermediate range of initial conditions, highlighted in yellow in figure 5. Otherwise, the drop collapses to one of the two single-phase limits, 
$\delta \rightarrow 0$ and 
$\delta \rightarrow 1$, leading to a flow configuration that does not entail a Taylor drop and is hence beyond the scope of this study.
Figure 5. Transient evolution of the Taylor drop thickness as a function of time computed by solving the energy balance in the non-dissipative regime in the interval 
$t=[t_0,10^5]$ with 
$t_0=10$. The plot shows the viscous limit 
$Ri\rightarrow \infty$ (solid line) and the cases with 
$Ri=1$ and 
$\mathcal {R}=0.8$ (dashed lines).
The transient dynamics is controlled by 
$M$ and 
$Ri$. When 
$Ri\rightarrow \infty$, a stable Taylor drop forms for initial thicknesses between 
$0.4<\delta <0.76$. The width of the stable region increases for 
$M\leq 1$ and widens up to 
$0<\delta <0.76$ in the free-surface limit. The free-surface limit is hence the most robust configuration and strongly favours the formation of a stable Taylor drop.
At steady state, both the ascending and the descending fluids occupy half of the cross-sectional area, 
$A_a/A_d=1$, and the energy balance (3.24) reduces to
\begin{equation} \frac{\partial \mathcal{P}}{\partial t} ({\delta_\infty})=0, \quad \textrm{for}\ t\rightarrow \infty, \end{equation}revealing that the potential energy is constant with time. If we manipulate (4.1) using (2.22) and (3.15) we obtain
\begin{equation} - A_a V_f \left( V_f+V_t \right)=0, \quad \textrm{for}\ t\rightarrow \infty, \end{equation}
and see that the ascent speed is equal to the descent speed, 
$V_f=-V_t$. This means that the loss in potential energy at the ascending front is balanced by the gain in potential energy at the descending tail in the non-dissipative regime, see (3.15) with 
$A_a=A_d$ and 
$V_f=-V_t$. The speeds 
$V_f$ and 
$V_t$ depend on the viscosity ratio and can be computed by evaluating (2.18) and (2.19) at 
$\delta _\infty =\sqrt {2}/{2}$ as
\begin{gather} V_f= \frac{(6+2M)\log 2 -M-4}{48+16M}, \end{gather}
\begin{gather}V_t=-\frac{(6+2M)\log 2 -M -4}{48+16M} . \end{gather}In the dissipative regime, the transient behaviour is qualitatively similar (see figure 6), but the steady-state solution is determined by the interplay of three mechanisms: the loss in potential energy at the ascending front; the gain in potential energy at the descending tail; and viscous dissipation. The energy balance (3.24) is
\begin{equation} \frac{\partial \mathcal{P}}{\partial t} ({\delta_\infty})=-(1-\mathcal{R})\varPhi({\delta_\infty})\quad \textrm{for}\ t\rightarrow \infty, \end{equation}
indicating that the potential energy decreases with time due to dissipation. Substituting (3.15) and (3.19) into (4.5) and using (2.22), we find that the steady-state solution is 
$\delta _{\infty }=\sqrt {2\mathcal {R}}/2$. Since 
$\mathcal {R}<1$, the viscous dissipation causes the drop to shrink and flow faster than in the non-dissipative regime, see figure 7(a). In fact, the ascending fluid occupies less than half of the cross-section, 
$A_a(\delta _\infty )/A=\mathcal {R}/2$, and, therefore, 
$V_f>|{V_t}|$, as evident from (2.22)
\begin{equation} \frac{V_t}{V_f}=- \frac{A_a}{A_d}= -\frac{\mathcal{R}}{2-\mathcal{R}},\quad \textrm{with}\ \delta_\infty=\frac{\sqrt{2\mathcal{R}}}{2}, \end{equation}
where 
$V_f(M,\mathcal {R})$ and 
$V_t(M,\mathcal {R})$ are calculated from (2.18) and (2.19). Note that the ascent speed is approximately one order of magnitude higher in the free-surface limit than in the rigid-core limit for almost the entire range of density ratios as shown in figure 7(b).
Figure 6. Transient evolution of the drop thickness as a function of time computed by solving the energy balance with viscous dissipation in the interval 
$t=[t_0,10^5]$ with 
$t_0=10$. The plot shows the viscous limit 
$Ri\rightarrow \infty$ and the effect of the density ratio 
$\mathcal {R}$. Solid lines have 
$\mathcal {R}=0.85$ and dashed lines have 
$\mathcal {R}=0.75$.
Figure 7. (a) Drop thickness and ratio of descent to ascent speed as a function of the density ratio for the dissipative regime. (b) Ascent speed 
$V_f$ as a function of the density and viscosity ratios for the dissipative regime.
Our findings extend the classical results of Benjamin (Reference Benjamin1968) for horizontal gravity currents to the vertical configuration. Benjamin (Reference Benjamin1968) showed that an inviscid bubble propagating in a horizontal tube has a dimensionless thickness of 
$1/2$. The thickness reduces when dissipation is accounted for, as demonstrated by Shin, Dalziel & Linden (Reference Shin, Dalziel and Linden2004). In this work, we observe the same qualitative trend for a liquid elongated drop formed in vertical pipe.
4.2. Validation against lock-exchange experiments
We validate our model against the experiments by Stevenson & Blake (Reference Stevenson and Blake1998) that measured the ascent speed of a Taylor drop formed from a lock-exchange configuration for different combinations of high-viscosity fluids. The experiments cover viscosity ratios of 
$M= 30{-}O(10^5)$ at high Bond number, 
$Bo\gg 1$. Here, we only consider experiments where a stable drop has formed to ensure that our model is applicable. For these experiments, the drops are elongated enough such that 
$\varepsilon \ll 1$ and the Archimedes number is sufficiently small, 
$Ar= O(10^{-5})\text{--}O(10^{-1})$. We list all the details of the experiments used for the validation in table 3.
Table 3. Dimensionless numbers, ascent speed and drop thickness of the experiments used for validating the model. The data of Stevenson & Blake (Reference Stevenson and Blake1998) are obtained with miscible fluids, 
$Bo\gg 1$, while the data of Goldsmith & Mason (Reference Goldsmith and Mason1962) are for immiscible fluids with 
$Bo\approx 1.3$.
Figure 8(a) shows that the measured ascent speed (solid circles) saturates around a constant value when the viscosity ratio is sufficiently large. Our model captures this trend well. When neglecting dissipation, our model slightly underestimates 
$V_f$, but it agrees well with the experiments in the dissipative regime. All the curves in figure 8(a) indicate that the drop's speed reaches a plateau when approaching the rigid-core and the free-surface limits. The transition between the two asymptotic behaviours occurs around 
$M= O(1){-}O(10)$.
Figure 8. (a) Ascent speed 
$V_f$ as a function of the viscosity ratio 
$M$. (b) Taylor drop thickness at the steady-state 
$\delta _\infty$ as a function of the viscosity ratio 
$M$. The solid line is the energy balance (3.21). The experimental data from Stevenson & Blake (Reference Stevenson and Blake1998) are lock-exchange experiments (the empty circles) and long drops (solid circles). The data from Goldsmith & Mason (Reference Goldsmith and Mason1962) are elongated drops.
The model also approximately matches the measured drop thicknesses in the dissipative regime as demonstrated in figure 8(b). Stevenson & Blake (Reference Stevenson and Blake1998) observed that the drops evolve to a uniform thickness around 
$\delta _\infty \approx 0.6$. Our energy analysis predicts 
$\delta _\infty$ within 
${\pm }15\,\%$ of the experimental value in the range of 
$\mathcal {R}\approx 0.7\text {--}0.9$, see figure 9. We consider this agreement satisfactory, particularly considering that the model is purely predictive and does not require any fitting parameters. For a more complete test of our model results, more experiments at intermediate 
$M$ would be valuable to better characterize the transition between drop behaviour in the rigid-core and the free-surface limits.
Figure 9. Comparison between the computed drop thickness at steady state 
$\delta _\infty$ and experimental measurements of drop thickness in the dissipative regime. The experimental data from Stevenson & Blake (Reference Stevenson and Blake1998) are lock-exchange experiments (the empty circles) and isolated drops (solid circles). The data from Goldsmith & Mason (Reference Goldsmith and Mason1962) are long drops. Dashed lines represent 
${\pm }15\,\%$ of the exact agreement between theoretical and experimental values.
4.3. Isolated Taylor drop
We refer to a Taylor drop as isolated when the tail is a closed interface and does not touch the wall. In addition to lock-exchange experiments, Stevenson & Blake (Reference Stevenson and Blake1998) injected a long drop at the bottom of the vertical pipe. They showed that the ascent speed of an isolated Taylor drop is indistinguishable from a drop formed from the lock-exchange configuration, see the solid circles in figure 8. Motivated by these observations, we compare the predictions of the ascent speed 
$V_f$ for a lock-exchange configuration with experimental data of isolated Taylor drops. Among the experiments of isolated Taylor drops available in the literature we use data from Stevenson & Blake (Reference Stevenson and Blake1998) and Goldsmith & Mason (Reference Goldsmith and Mason1962), see table 3. Although Kurimoto et al. (Reference Kurimoto, Hayashi and Tomiyama2013) and Hayashi et al. (Reference Hayashi, Kurimoto and Tomiyama2011) measured the ascent speed of Taylor drops covering a wide range of 
$Ar=O(10)\text{--}O(5000)$, 
$M=O(0.1)\text{--}O(10)$, 
$Bo=O(1)\text{--}O(10)$ and 
$R\approx 0.8$, our model does not apply to their experiments, because the drops are not long enough to fulfil the requirement that 
$\varepsilon \ll 1$ and 
$\varepsilon Ar \ll 1$.
Figure 9 compares theoretical and experimental drop thicknesses, demonstrating that our model agrees well with observations. The 
$\delta _\infty$ measured by Goldsmith & Mason (Reference Goldsmith and Mason1962) is very close to 
$\sqrt {2}/2$ and it is within 
${\pm }15\,\%$ error if we account for viscous dissipation. More interestingly, we can see in figure 8 that the isolated drop data confirms the existence of the two plateaus at 
$M\rightarrow 0$ and 
$M\rightarrow \infty$.
The insight that our model also describes isolated Taylor drops suggests that we can apply it to slug flow, defined as an intermittent flow pattern that consists of a train of isolated Taylor bubbles or drops. It is common practice in the literature (Wallis Reference Wallis1969; Fabre & Line Reference Fabre and Line1992; Brauner & Ullmann Reference Brauner and Ullmann2004; Picchi et al. Reference Picchi, Manerba, Correra, Margarone and Poesio2015) to model slug flow using the correlation by Nicklin, Wilkes & Davidson (Reference Nicklin, Wilkes and Davidson1962). This correlation requires a model for the ascent speed, referred as drift velocity in Nicklin et al. (Reference Nicklin, Wilkes and Davidson1962) and identical to the dimensional ascent speed at steady state in our model. To the best of our knowledge, the drift velocity of isolated Taylor drops has only been characterized experimentally (e.g. Wallis Reference Wallis1969; Fabre & Line Reference Fabre and Line1992), but it has not yet been formulated from first principles.
To fill this gap, we propose to estimate the drift velocity in the non-dissipative regime using (4.3)
\begin{equation} \hat{V}_f=\left( \frac{{\rm \Delta} \rho g R^2}{\mu_d}\right) \frac{(6+2M)\log 2 -M-4}{48+16M}. \end{equation}This formula converges to the scaling obtained for the ascent speed of Taylor bubbles in the laminar regime by Wallis (Reference Wallis1969) and Brauner & Ullmann (Reference Brauner and Ullmann2004),
\begin{equation} \hat{V}_f(M\rightarrow \infty)=0.02414 \frac{{\rm \Delta} \rho g R^2}{\mu_d}. \end{equation}
In the dissipative regime, the drift velocity in slug flow can be estimated by evaluating (2.18) at 
$\delta _\infty =\sqrt {2\mathcal {R}}/2$.
4.4. Backflow and velocity profiles
The rise of a Taylor drop may lead to backflow in one of two fluids. If the speed at the fluid–fluid interface, 
$u_{in}=u_a(\delta )=u_d(\delta )$, is less than zero, backflow occurs in the ascending fluid. Despite the ascent speed of the ascending fluid being positive, the local velocity assumes a negative value near the interface, highlighting that a portion of the light fluid is dragged downward. The backflow occurs inside the drop as long as 
$M>0.26$ (see figure 10a). When 
$M<0.26$, the ascending fluid drags a portion of the heavy fluid upward and backflow occurs in the descending fluid. The switching point is at 
$M=0.26$, which corresponds to the case of a static interface 
$u_{in}=0$ (see figure 10a).
Figure 10. (a) Interfacial speed 
$u_{in}$ as a function of the viscosity ratio 
$M$ for the steady state configuration 
$\delta _{\infty }=\sqrt {2}/{2}$ (non-dissipative regime). (b) Velocity profiles of the steady state configuration for different viscosity ratio 
$M$ in the non-dissipative regime.
Figure 10(b) shows the steady-state velocity profiles, (2.14a) and (2.14b), for the entire range of viscosity ratios in the non-dissipative regime. It highlights that the velocity profiles converge to the limiting cases of 
$M \rightarrow \infty$ relatively quickly. In this limit, the velocity profile of the descending fluid resembles that of a free-surface flow. Instead, for 
$M\rightarrow 0$, the ascending fluid is so viscous that the velocity profile is almost flat. In the dissipative regime, the drop shrinks and the velocity profile changes as depicted in figure 11(b). Since 
$\delta _\infty < \sqrt {2}/2$, the maximal speed at the pipe centre is higher compared with the non-dissipative regime. Also, the magnitude of the interfacial speed increases with the density difference between the fluids, extending the backflow in the descending fluids to higher 
$M$ compared with the dissipative regime, see figure 11(a).
Figure 11. (a) Interfacial speed 
$u_{in}$ as a function of the viscosity ratio 
$M$ and the density ratio 
$\mathcal {R}$ at steady state 
$\delta _{\infty }=\sqrt {2\mathcal {R}}/{2}$ for the dissipative regime. (b) Velocity profiles at steady state for different viscosity ratio 
$M$ in the dissipative regime for 
$\mathcal {R}=0.7$.
Our results agree well with the measurements of Goldsmith & Mason (Reference Goldsmith and Mason1962). Figure 12 shows the comparison between the velocity profiles in the axial direction of an isolated Taylor drop measured by Goldsmith & Mason (Reference Goldsmith and Mason1962) for two specific viscosity ratios. The solid curves represent the model predictions in the non-dissipative regime. The model reproduces not only the measured velocity profile, but it also confirms the switching between the two backflow scenarios. For 
$M=0.91$, backflow occurs in the ascending fluid (see figure 12a), but has shifted into the descending fluid for 
$M=0.12$ (figure 12b). These results are consistent with the theoretical switching point at 
$M=0.26$ and validate the velocity profiles predicted by the model, obtained without any fitting parameter. Our predicted behaviour in the free-surface limit also agrees well with the numerical simulations of Suckale et al. (Reference Suckale, Qin, Picchi, Keller and Battiato2018).
Figure 12. Comparison of measured and modelled velocity profiles for the experiments of Goldsmith & Mason (Reference Goldsmith and Mason1962) for 
$M=0.91$ (a) and 
$M=0.12$ (b).
4.5. Implications for persistently active volcanoes
In upward and downward inclined flows, multiple configurations may exist for fixed operational conditions (Barnea & Taitel Reference Barnea and Taitel1992; Ullmann et al. Reference Ullmann, Zamir, Ludmer and Brauner2003b; Thibault, Munoz & Liné Reference Thibault, Munoz and Liné2015; Picchi & Poesio Reference Picchi and Poesio2016; Goldstein, Ullmann & Brauner Reference Goldstein, Ullmann and Brauner2017; Picchi et al. Reference Picchi, Poesio, Ullmann and Brauner2017, Reference Picchi, Barmak, Ullmann and Brauner2018a; Picchi, Ullmann & Brauner Reference Picchi, Ullmann and Brauner2018b). For given fluids flow rates, there exist multiple steady-state solutions that differ in the volume fractions, velocity profiles and the pressure drop, but share the same flux. Recent experiments suggest that different configurations may also coexist in the pipe (Ullmann et al. Reference Ullmann, Zamir, Gat and Brauner2003a). Understanding the existence and stability of multiple flow solutions is of particular interest in the volcanological context, because persistently active volcanoes display a wide range of eruptive regimes which are thought to represent different flow configurations in the conduit (e.g. Vergniolle & Mangan Reference Vergniolle and Mangan2000).
Suckale et al. (Reference Suckale, Qin, Picchi, Keller and Battiato2018) showed that vertical core-annular flow admits two steady-state configurations with the same flux, a solution with fast flow in a thin core and a solution with relatively slow flow in a thick core. Both solutions appear to be realized in the core-annular flow experiments by Beckett et al. (Reference Beckett, Mader, Phillips, Rust and Witham2011), which involved two large tanks connected by an open pipe. However, only the thick-core solution appears to be physically realized in the lock-exchange set-up of Stevenson & Blake (Reference Stevenson and Blake1998). The experimental set-up of Stevenson & Blake (Reference Stevenson and Blake1998) is a closed pipe and the observed flow regime is a Taylor drop instead of core-annular flow.
Here, we show that the presence of a propagating interface (i.e. the Taylor drop) breaks the symmetry between the two solutions derived in Suckale et al. (Reference Suckale, Qin, Picchi, Keller and Battiato2018). We find that, for the experiments by Stevenson & Blake (Reference Stevenson and Blake1998), the energy balance favours a Taylor drop with a constant thickness of 
$\sqrt {2\mathcal {R}}/{2}$, particularly at high viscosity contrast 
$M \gg 1$ (see figure 6c). At smaller viscosity contrast, 
$M\approx 1$, there is a much wider range of initial configurations that do not lead to the formation of a stable Taylor drop (see figure 6b). Applied to the volcanic context, this finding suggests that exchange flow in the lava conduit is most prone to instability in the vicinity of the uppermost portion of the conduit, where the viscosity of the two magmatic fluids becomes comparable as the ascending magma loses its volatiles through degassing. Interestingly, mildly eruptive behaviour such as normal eruptions at Stromboli volcano, Italy, tend to originate at relatively shallow depths (e.g. Harris & Ripepe Reference Harris and Ripepe2007).
5. Conclusions
In this paper, we study the ascent dynamics of a Taylor drop formed from a lock-exchange configuration in a closed vertical pipe. We derive an analytical formulation of the ascent speed in the viscous regime that is consistent with laboratory experiments by combining a lubrication model with the energy balance for the entire system. We show that Taylor drops reach a thickness of 
$\sqrt {2}/2$ in steady-state when neglecting dissipation and assume a slightly lower value, 
$\sqrt {2\mathcal {R}}/2$, when dissipation is accounted for. The ascent speed is proportional to the dimensional group 
${\rm \Delta} \rho g R^2/\mu _d$ and depends on the viscosity ratio in the non-dissipative regime and on both the viscosity ratio and the density ratio in the dissipative regime.
Our study also clarifies that, once the Taylor drop reaches the terminal speed, the system finds an energetic equilibrium. In the non-dissipative regime, the speed at the front equals the speed of the tail and each fluid occupies half of the cross-section of the pipe. In this regime, the ascent dynamics is controlled by the balance of two mechanisms: the loss in the potential energy due to the interpenetration of the lighter fluid into the heavy fluid and the gain in potential energy due to the displacement of the lighter fluid by the heavy fluid. In the dissipative regime, dissipation is a third mechanism that needs to be considered. It causes the drop to shrink and flow faster compared with the non-dissipative regime.
The viscosity ratio controls where backflow occurs. When the viscosity ratio exceeds a threshold value, it occurs inside the drop. Otherwise, backflow switches to the surrounding fluid. Our results have implications for the determination of the drift velocity of a Taylor drop in slug flows and our understanding of conduit flow in persistently degassing volcanoes.
Acknowledgements
D.P. and I.B. were supported by the Department of Energy under the Early Career Award DE-SC0014227. We also thank the anonymous reviewers for their careful reading of our manuscript and their many insightful comments and suggestions.
Declaration of interests
The authors report no conflict of interest.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2020.596.
Appendix A. Expressions for $g(\delta ,t)$ and $f(\delta ,t)$
Here, we report the analytical expressions of the derivatives in 
$g(\delta ,t)$ as follows:
\begin{align} \frac{\partial \mathcal{E}}{\partial t} &= {\rm \pi}\frac{(V_f-V_t)}{96 } \left[ \left(\frac{1}{\mathcal{R}-1}-\delta^6-3 \delta^4-3\delta^2 \right)P^2 +12(\log\delta)^2 \left( \delta^6 + \frac{\delta^4}{\mathcal{R}-1}\right) \right. \nonumber\\ &\quad \left. -6\delta^2P\log\delta \left( \delta^4-2\delta^2 -\frac{1}{\mathcal{R}-1}\right) \right], \end{align}
\begin{equation} \frac{\partial \mathcal{P}}{\partial t}= {\rm \pi}\left[ \delta^2 V_t^2 - (1-\delta^2) V_f^2\right]t . \end{equation}
We obtain the term 
$g(\delta ,t)$ by combining (A 1) and (A 2) with (2.18) and (2.19) as follows:
\begin{equation} g(\delta,t)=\frac{1}{Ri}\frac{\partial \mathcal{E}}{\partial t}+\frac{\partial \mathcal{P}}{\partial t}. \end{equation}
We compute 
$f(\delta ,t)$ analytically using the chain rule for derivatives of composite functions on 
$\mathcal {E}=\mathcal {E}(\delta ,t, V_f(\delta ),V_t(\delta ) )$ and 
$\mathcal {P}=\mathcal {P}(\delta ,t, V_f(\delta ),V_t(\delta ) )$. Since the analytical expression is quite cumbersome, we do not detail it in the paper but it is available as a Maple file in the supplementary material available at https://doi.org/10.1017/jfm.2020.596.
Appendix B. Energy balance: high $Ri$ limit
In the limit of 
$Ri \rightarrow \infty$, the energy balance (3.24) can be recast as
\begin{equation} \frac{\textrm{d} \delta}{\textrm{d} t}= -\frac{(1-\mathcal{R})\varPhi+ \dfrac{\partial \mathcal{P}}{\partial t} }{\dfrac{\partial \mathcal{P}}{\partial \delta}}, \end{equation}
where 
$\partial \mathcal {P}/\partial t$ is given by (A 2) and 
$\varPhi$ is given by (3.18). The term 
$\partial \mathcal {P}/\partial \delta$ has to be calculated using the chain rule for derivatives of composite functions on 
$\mathcal {P}=\mathcal {P}(\delta ,t, V_f(\delta ),V_t(\delta ) )$. We performed the computation using the software Maple (the Maple file is available in the supplementary material of this manuscript). With this, (B 1) becomes
\begin{equation} \frac{\textrm{d} \delta}{\textrm{d} t}=\frac{a_1}{ ta_2}, \end{equation}where
\begin{align} a_1 &= \delta(\delta^2-1)(\psi-2\delta^2) [(M-1)\delta^4+1] \left[ \left( (M-1)\delta^4+1\right)\log{\delta} \vphantom{\left(1-\frac{3M}{4} \right)}\right. \nonumber\\ &\quad \left. +\left(1-\frac{3M}{4} \right)\delta^4+(M-2)\delta^2-\frac{M}{4}+1 \right], \end{align}
\begin{align} a_2 &= \left[(M-1)\delta^4+1\right]^2 \left( 6\delta^4-10\delta^2+3\right) \log{\delta} \nonumber\\ &\quad - \frac{1}{4}(\delta^2-1) \left[ \left( 10M^2-26M+16\right)\delta^{10}+ \left( -16M^2+44M-28 \right)\delta^8 \right.\nonumber\\ &\quad \left. +\left( 3M^2+19M-36 \right)\delta^6+\left( M^2-61M+108 \right)\delta^4 \right. \nonumber\\ &\quad \left. +\left (27M-76\right)\delta^2-3M+16\right] \end{align}and
\begin{gather} \psi=1 \quad \textrm{when}\ \varPhi=0, \end{gather}
\begin{gather}\psi=\mathcal{R} \quad \textrm{when}\ \varPhi\neq 0. \end{gather}
Open access
