Published online by Cambridge University Press: 15 May 2019
Flow visualization and particle image velocimetry (PIV) measurements are used to unravel the pattern transition and velocity field in the Taylor–Couette flow (TCF) of neutrally buoyant non-Brownian spheres immersed in a Newtonian fluid. With increasing Reynolds number (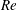 $Re$) or the rotation rate of the inner cylinder, the bifurcation sequence in suspension TCF remains same as in its Newtonian counterpart (i.e. from the circular Couette flow (CCF) to stationary Taylor vortex flow (TVF) and then to travelling wavy Taylor vortices (WTV) with increasing
$Re$) or the rotation rate of the inner cylinder, the bifurcation sequence in suspension TCF remains same as in its Newtonian counterpart (i.e. from the circular Couette flow (CCF) to stationary Taylor vortex flow (TVF) and then to travelling wavy Taylor vortices (WTV) with increasing 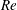 $Re$) for small particle volume fractions (
$Re$) for small particle volume fractions (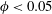 $\unicode[STIX]{x1D719}<0.05$). However, at
$\unicode[STIX]{x1D719}<0.05$). However, at 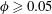 $\unicode[STIX]{x1D719}\geqslant 0.05$, non-axisymmetric patterns such as (i) the spiral vortex flow (SVF) and (ii) two mixed or co-existing states of stationary (TVF, axisymmetric) and travelling (WTV or SVF, non-axisymmetric) waves, namely (iia) the ‘TVF
$\unicode[STIX]{x1D719}\geqslant 0.05$, non-axisymmetric patterns such as (i) the spiral vortex flow (SVF) and (ii) two mixed or co-existing states of stationary (TVF, axisymmetric) and travelling (WTV or SVF, non-axisymmetric) waves, namely (iia) the ‘TVF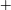 $+$WTV’ and (iib) the ‘TVF
$+$WTV’ and (iib) the ‘TVF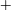 $+$SVF’ states, are found, with the former as a primary bifurcation from CCF. While the SVF state appears both in the ramp-up and ramp-down experiments as in the work of Majji et al. (J. Fluid Mech., vol. 835, 2018, pp. 936–969), new co-existing patterns are found only during the ramp-up protocol. The secondary bifurcation TVF
$+$SVF’ states, are found, with the former as a primary bifurcation from CCF. While the SVF state appears both in the ramp-up and ramp-down experiments as in the work of Majji et al. (J. Fluid Mech., vol. 835, 2018, pp. 936–969), new co-existing patterns are found only during the ramp-up protocol. The secondary bifurcation TVF 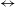 $\leftrightarrow$ WTV is found to be hysteretic or sub-critical for
$\leftrightarrow$ WTV is found to be hysteretic or sub-critical for 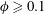 $\unicode[STIX]{x1D719}\geqslant 0.1$. In general, there is a reduction in the value of the critical Reynolds number, i.e.
$\unicode[STIX]{x1D719}\geqslant 0.1$. In general, there is a reduction in the value of the critical Reynolds number, i.e.  $Re_{c}(\unicode[STIX]{x1D719}\neq 0)<Re_{c}(\unicode[STIX]{x1D719}=0)$, for both primary and secondary transitions. The wave speeds of both travelling waves (WTV and SVF) are approximately half of the rotational velocity of the inner cylinder, with negligible dependence on
$Re_{c}(\unicode[STIX]{x1D719}\neq 0)<Re_{c}(\unicode[STIX]{x1D719}=0)$, for both primary and secondary transitions. The wave speeds of both travelling waves (WTV and SVF) are approximately half of the rotational velocity of the inner cylinder, with negligible dependence on  $\unicode[STIX]{x1D719}$. The analysis of the radial–axial velocity field reveals that the Taylor vortices in a suspension are asymmetric and become increasingly anharmonic, with enhanced radial transport, with increasing particle loading. Instantaneous streamline patterns on the axial–radial plane confirm that the stationary Taylor vortices can indeed co-exist either with axially propagating spiral vortices or azimuthally propagating wavy Taylor vortices – their long-time stability is demonstrated. It is shown that the azimuthal velocity is considerably altered for
$\unicode[STIX]{x1D719}$. The analysis of the radial–axial velocity field reveals that the Taylor vortices in a suspension are asymmetric and become increasingly anharmonic, with enhanced radial transport, with increasing particle loading. Instantaneous streamline patterns on the axial–radial plane confirm that the stationary Taylor vortices can indeed co-exist either with axially propagating spiral vortices or azimuthally propagating wavy Taylor vortices – their long-time stability is demonstrated. It is shown that the azimuthal velocity is considerably altered for  $\unicode[STIX]{x1D719}\geqslant 0.05$, resembling shear-band type profiles, even in the CCF regime (i.e. at sub-critical Reynolds numbers) of suspension TCF; its possible role on the genesis of observed patterns as well as on the torque scaling is discussed.
$\unicode[STIX]{x1D719}\geqslant 0.05$, resembling shear-band type profiles, even in the CCF regime (i.e. at sub-critical Reynolds numbers) of suspension TCF; its possible role on the genesis of observed patterns as well as on the torque scaling is discussed.