Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-16T18:25:40.919Z Has data issue: false hasContentIssue false
  • English
  • Français

Suppression of the Kapitza instability in confined falling liquid films

Published online by Cambridge University Press:  07 December 2018

Gianluca Lavalle Open the ORCID record for Gianluca Lavalle [Opens in a new window] ,
Yiqin Li ,
Sophie Mergui ,
Nicolas Grenier  and
Georg F. Dietze Open the ORCID record for Georg F. Dietze [Opens in a new window]
Gianluca Lavalle*
Affiliation:
Laboratoire LIMSI, CNRS, Univ. Paris-Sud, Université Paris-Saclay, F-91405, Orsay, France
Yiqin Li
Affiliation:
Laboratoire FAST, Univ. Paris-Sud, CNRS, Université Paris-Saclay, F-91405, Orsay, France
Sophie Mergui
Affiliation:
Laboratoire FAST, Univ. Paris-Sud, CNRS, Université Paris-Saclay, F-91405, Orsay, France
Nicolas Grenier
Affiliation:
Laboratoire LIMSI, CNRS, Univ. Paris-Sud, Université Paris-Saclay, F-91405, Orsay, France
Georg F. Dietze
Affiliation:
Laboratoire FAST, Univ. Paris-Sud, CNRS, Université Paris-Saclay, F-91405, Orsay, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We revisit the linear stability of a falling liquid film flowing through an inclined narrow channel in interaction with a gas phase. We focus on a particular region of parameter space, small inclination and very strong confinement, where we have found the gas to strongly stabilize the film, up to the point of fully suppressing the long-wave interfacial instability attributed to Kapitza (Zh. Eksp. Teor. Fiz., vol. 18 (1), 1948, pp. 3–28). The stabilization occurs both when the gas is merely subject to an aerostatic pressure difference, i.e. when the pressure difference balances the weight of the gas column, and when it flows counter-currently. In the latter case, the degree of stabilization increases with the gas velocity. Our investigation is based on a numerical solution of the Orr–Sommerfeld temporal linear stability problem as well as stability experiments that clearly confirm the observed effect. We quantify the degree of stabilization by comparing the linear stability threshold with its passive-gas limit, and perform a parametric study, varying the relative confinement, the Reynolds number, the inclination angle and the Kapitza number. For example, we find a 30 % reduction of the cutoff wavenumber of the instability for a water film in contact with air, flowing through a channel inclined at 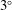$3^{\circ }$ and of height 2.8 times the film thickness. We also identify the critical conditions for the full suppression of the instability in terms of the governing parameters. The stabilization is caused by the strong confinement of the gas, which produces perturbations of the adverse interfacial tangential shear stress that are shifted by half a wavelength with respect to the wavy film surface. This tends to reduce flow-rate variations within the film, thus attenuating the inertia-based driving mechanism of the Kapitza instability.

JFM classification

Multiphase and Particle-laden Flows: Gas/liquid flow Instability: Instability Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 860 , 10 February 2019 , pp. 608 - 639
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alekseenko, S. V., Aktershev, S. P., Cherdantsev, A. V., Kharlamov, S. M. & Markovich, D. M. 2009 Primary instabilities of liquid film flow sheared by turbulent gas stream. Intl J. Multiphase Flow 35, 617–627.Google Scholar
Alekseenko, S. V., Nakoryakov, V. Ye. & Pokusaev, B. G. 1985 Wave formation on a vertical falling liquid film. AIChE J. 31 (9), 1446–1460.Google Scholar
Anshus, B. E. & Goren, S. L. 1966 A method of getting approximate solutions to the Orr–Sommerfeld equation for flow on a vertical wall. AIChE J. 12, 1004–1008.Google Scholar
Benjamin, T. B. 1957 Wave formation in laminar flow down an inclined plane. J. Fluid Mech. 2, 554–574.Google Scholar
Bergé, P., Pomeau, Y. & Vidal, C. 1988 L’Ordre dans le Chaos, 5th edn. Hermann.Google Scholar
Boomkamp, P. A. M. & Miesen, R. H. M. 1996 Classification of instabilities in parallel two-phase flow. Intl J. Multiphase Flow 22, 67–88.Google Scholar
Brevdo, L., Laure, P., Dias, F. & Bridges, T. J. 1999 Linear pulse structure and signalling in a film flow on an inclined plane. J. Fluid Mech. 396, 37–71.Google Scholar
Cohen-Sabban, J., Gaillard-Groleas, J. & Crepin, P.-J. 2001 Quasi-confocal extended field surface sensing. In Optical Metrology Roadmap for the Semiconductor, Optical, and Data Storage Industries II (ed. Duparre, A. & Singh, B.), Proceedings of SPIE, vol. 4449, pp. 178–183. Society of Photo-optical Instrumentation Engineers.Google Scholar
Dietze, G. F. 2016 On the Kapitza instability and the generation of capillary waves. J. Fluid Mech. 789, 368–401.Google Scholar
Dietze, G. F. & Ruyer-Quil, C. 2013 Wavy liquid films in interaction with a confined laminar gas flow. J. Fluid Mech. 722, 348–393.Google Scholar
Doedel, E. J. 2008 AUTO-07p: Continuation and Bifurcation Software for Ordinary Differential Equations. Montreal Concordia University.Google Scholar
Floryan, J. M., Davis, S. H. & Kelly, R. E. 1987 Instabilities of a liquid film flowing down a slightly inclined plane. Phys. Fluids 30 (4), 983–989.Google Scholar
Gaster, M. 1962 A note on the relation between temporally increasing and spatially increasing disturbances in hydrodynamic stability. J. Fluid Mech. 14, 222–224.Google Scholar
Hinch, E. J. 1984 A note on the mechanism of the instability at the interface between two shearing fluids. J. Fluid Mech. 144, 463–465.Google Scholar
Kalliadasis, S., Ruyer-Quil, C., Scheid, B. & Velarde, M. G. 2012 Falling Liquid Films. Springer.Google Scholar
Kapitza, P. L. 1948 Wave flow of thin layers of a viscous fluid (in Russian). Zh. Eksp. Teor. Fiz. 18 (1), 3–28.Google Scholar
Kelly, R. E., Goussis, D. A., Lin, S. P. & Hsu, F. K. 1989 The mechanism for surface wave instability in film flow down an inclined plane. Phys. Fluids A 1 (5), 819–826.Google Scholar
Kofman, N.2014, Films liquides tombants avec ou sans contre-écoulement de gaz: application au problème de l’engorgement dans les colonnes de distillation. PhD thesis, Université Pierre et Marie Curie.Google Scholar
Kofman, N., Mergui, S. & Ruyer-Quil, C. 2017 Characteristics of solitary waves on a falling liquid film sheared by a turbulent counter-current gas flow. Intl J. Multiphase Flow 95, 22–34.Google Scholar
Krantz, W. B. & Goren, S. L. 1971 Stability of thin liquid films flowing down a plane. Ind. Engng Chem. Fundam. 10, 91–101.Google Scholar
Lavalle, G., Vila, J. P., Lucquiaud, M. & Valluri, P. 2017 Ultraefficient reduced model for countercurrent two-layer flows. Phys. Rev. Fluids 2, 014001.Google Scholar
Liu, J., Paul, J. D. & Gollub, J. P. 1993 Measurements of the primary instabilities of film flows. J. Fluid Mech. 250, 69–101.Google Scholar
Ó Náraigh, L., Spelt, P. D. M. & Shaw, S. J. 2013 Absolute linear instability in laminar and turbulent gas–liquid two-layer channel flow. J. Fluid Mech. 714, 58–94.Google Scholar
Pierson, F. W. & Whitaker, S. 1977 Some theoretical and experimental observations of the wave structure of falling liquid films. Ind. Engng Chem. Fundam. 16, 401–408.Google Scholar
Ruyer-Quil, C. & Manneville, P. 2000 Improved modeling of flows down inclined planes. Eur. Phys. J. B 15, 357–369.Google Scholar
Samanta, A. 2014 Shear-imposed falling film. J. Fluid Mech. 753, 131–149.Google Scholar
Schmidt, P., Ó Náraigh, L., Lucquiaud, M. & Valluri, P. 2016 Linear and nonlinear instability in vertical counter-current laminar gas–liquid flows. Phys. Fluids 28, 042102.Google Scholar
Smith, M. K. 1990 The mechanism for the long-wave instability in thin liquid films. J. Fluid Mech. 217, 469–485.Google Scholar
Tilley, B. S., Davis, S. H. & Bankoff, S. G. 1994 Linear stability theory of two-layer fluid flow in an inclined channel. Phys. Fluids 6 (12), 3906–3922.Google Scholar
Trifonov, Y. Y. 2010 Counter-current gas–liquid wavy film flow between the vertical plates analyzed using the Navier–Stokes equations. AIChE J. 56 (8), 1975–1987.Google Scholar
Trifonov, Y. Y. 2017 Instabilities of a gas–liquid flow between two inclined plates analyzed using the Navier–Stokes equations. Intl J. Multiphase Flow 95, 144–154.Google Scholar
Valluri, P., Ó Náraigh, L., Ding, H. & Spelt, P. D. M. 2010 Linear and nonlinear spatio-temporal instability in laminar two-layer flows. J. Fluid Mech. 656, 458–480.Google Scholar
Vellingiri, R., Tseluiko, D. & Kalliadasis, S. 2015 Absolute and convective instabilities in counter-current gas–liquid film flows. J. Fluid Mech. 763, 166–201.Google Scholar
Whitaker, S. 1964 Effect of surface active agents on the stability of falling liquid films. Ind. Engng Chem. Fundam. 3, 132–142.Google Scholar
Yiantsios, S. G. & Higgins, B. G. 1988 Linear stability of plane Poiseuille flow of two superposed fluids. Phys. Fluids 31 (11), 3225–3238.Google Scholar
Yiantsios, S. G. & Higgins, B. G. 1989 Erratum: ‘Linear stability of plane Poiseuille flow of two superposed fluids’ [Phys. Fluids 31, 3225 (1988)]. Phys. Fluids A 1 (5), 3225–3238.Google Scholar
Yih, C. S. 1963 Stability of liquid flow down an inclined plane. Phys. Fluids 6 (3), 321–334.Google Scholar
Yih, C. S. 1967 Instability due to viscosity stratification. J. Fluid Mech. 27, 337–352.Google Scholar