Published online by Cambridge University Press: 05 January 2017
We experimentally investigate mixing in sheared particulate suspensions by measuring a crucial kinematic quantity of the flow: the stretching laws of material lines in the suspending liquid. High-resolution particle image velocimetry (PIV) measurements in the fluid phase are performed to reconstruct, following the Diffusive Strip Method (Meunier & Villermaux, J. Fluid Mech., vol. 662, 2010, pp. 134–172), the stretching histories of the fluid material lines. In a broad range of volume fractions
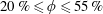 $20\,\%\leqslant \unicode[STIX]{x1D719}\leqslant 55\,\%$
, the nature of the elongation law changes drastically from linear, in the absence of particles, to exponential in the presence of particles: the mean and the standard deviation of the material line elongations are found to grow exponentially in time and the distribution of elongations converges to a log-normal. A multiplicative stretching model, based on the distribution of local shear rates and on their persistence time, is derived. This model quantitatively captures the experimental stretching laws. The presence of particles is shown to accelerate mixing at large Péclet numbers (
$20\,\%\leqslant \unicode[STIX]{x1D719}\leqslant 55\,\%$
, the nature of the elongation law changes drastically from linear, in the absence of particles, to exponential in the presence of particles: the mean and the standard deviation of the material line elongations are found to grow exponentially in time and the distribution of elongations converges to a log-normal. A multiplicative stretching model, based on the distribution of local shear rates and on their persistence time, is derived. This model quantitatively captures the experimental stretching laws. The presence of particles is shown to accelerate mixing at large Péclet numbers (
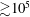 ${\gtrsim}10^{5}$
). However, the wide distribution of stretching rates results in heterogeneous mixing and, hence, broadly distributed mixing times, in qualitative agreement with experimental observations.
${\gtrsim}10^{5}$
). However, the wide distribution of stretching rates results in heterogeneous mixing and, hence, broadly distributed mixing times, in qualitative agreement with experimental observations.
Slice of a sheared suspension of volume fraction \phi=0.35 illuminated by a laser sheet. The small fluorescent tracers seeding the suspending fluid appear as bright whereas the particle intersections with the laser sheet appear as dark. The particle diametre d=2 mm.
Comparison of the stretching process of a blob of dye (in black) sheared at high Péclet (Pe=10^6) and low Reynolds number (Re=10^{-4}) in a pure fluid (top), and in a particulate suspension with volume fraction \phi=35\%.
Example of stretching for two material lines numerically advected using the experimental fluid velocity field. One line successively stretches and folds very similarly to what is observed in the blob experiments (Movie 2). Interestingly, the other line behaves very differently. Although it sustains the same macroscopic strain, it experiences a much softer stretching only because it started from a different initial location. These different stretching histories reveal the stochastic nature of the stretching induced within particulate suspensions.