Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Iungo, G. V.
Viola, F.
Camarri, S.
Porté-Agel, F.
and
Gallaire, F.
2013.
Linear stability analysis of wind turbine wakes performed on wind tunnel measurements.
Journal of Fluid Mechanics,
Vol. 737,
Issue. ,
p.
499.
Luchini, Paolo
and
Bottaro, Alessandro
2014.
Adjoint Equations in Stability Analysis.
Annual Review of Fluid Mechanics,
Vol. 46,
Issue. 1,
p.
493.
Trip, Renzo
and
Fransson, Jens H. M.
2014.
Boundary layer modification by means of wall suction and the effect on the wake behind a rectangular forebody.
Physics of Fluids,
Vol. 26,
Issue. 12,
Levy, B.
Friedrich, H.
Cater, J. E.
Clarke, R. J.
and
Denier, J. P.
2014.
The impact of twine/mesh ratio on the flow dynamics through a porous cylinder.
Experiments in Fluids,
Vol. 55,
Issue. 10,
Camarri, Simone
2015.
Flow control design inspired by linear stability analysis.
Acta Mechanica,
Vol. 226,
Issue. 4,
p.
979.
Meliga, P.
Boujo, E.
and
Gallaire, F.
2016.
A self-consistent formulation for the sensitivity analysis of finite-amplitude vortex shedding in the cylinder wake.
Journal of Fluid Mechanics,
Vol. 800,
Issue. ,
p.
327.
Oruç, Vedat
Akilli, Hüseyin
and
Sahin, Besir
2016.
PIV measurements on the passive control of flow past a circular cylinder.
Experimental Thermal and Fluid Science,
Vol. 70,
Issue. ,
p.
283.
Siconolfi, L.
Fani, A.
Camarri, S.
and
Salvetti, M.V.
2016.
Effect of geometry modifications on the engulfment in micromixers: Numerical simulations and stability analysis.
European Journal of Mechanics - B/Fluids,
Vol. 55,
Issue. ,
p.
360.
Tammisola, O.
and
Juniper, M. P.
2016.
Coherent structures in a swirl injector at Re = 4800 by nonlinear simulations and linear global modes.
Journal of Fluid Mechanics,
Vol. 792,
Issue. ,
p.
620.
Meliga, P.
Cadot, O.
and
Serre, E.
2016.
Experimental and Theoretical Sensitivity Analysis of Turbulent Flow Past a Square Cylinder.
Flow, Turbulence and Combustion,
Vol. 97,
Issue. 4,
p.
987.
Camarri, S.
Trip, R.
and
Fransson, J. H. M.
2017.
Investigation of passive control of the wake past a thick plate by stability and sensitivity analysis of experimental data.
Journal of Fluid Mechanics,
Vol. 828,
Issue. ,
p.
753.
Carini, M.
Airiau, C.
Debien, A.
Léon, O.
and
Pralits, J. O.
2017.
Global stability and control of the confined turbulent flow past a thick flat plate.
Physics of Fluids,
Vol. 29,
Issue. 2,
Camarri, Simone
and
Mengali, Giacomo
2019.
Stability properties of the mean flow after a steady symmetry-breaking bifurcation and prediction of the nonlinear saturation.
Acta Mechanica,
Vol. 230,
Issue. 9,
p.
3127.
Magri, Luca
2019.
Adjoint Methods as Design Tools in Thermoacoustics.
Applied Mechanics Reviews,
Vol. 71,
Issue. 2,
Pini, A.
Cammi, A.
Lorenzi, S.
Cauzzi, M.T.
and
Luzzi, L.
2019.
A CFD-based simulation tool for the stability analysis of natural circulation systems.
Progress in Nuclear Energy,
Vol. 117,
Issue. ,
p.
103093.
Giannetti, F.
Camarri, S.
and
Citro, V.
2019.
Sensitivity analysis and passive control of the secondary instability in the wake of a cylinder.
Journal of Fluid Mechanics,
Vol. 864,
Issue. ,
p.
45.
Leclercq, Colin
Demourant, Fabrice
Poussot-Vassal, Charles
and
Sipp, Denis
2019.
Linear iterative method for closed-loop control of quasiperiodic flows.
Journal of Fluid Mechanics,
Vol. 868,
Issue. ,
p.
26.
Grenga, T.
and
Mueller, M. E.
2020.
Data Analysis for Direct Numerical Simulations of Turbulent Combustion.
p.
157.
Jamshed, Saqib
and
Dhiman, Amit
2021.
Channel-Confined Wake Structure Interactions Between Two Permeable Side-by-Side Bars of a Square Cross-Section.
Journal of Fluids Engineering,
Vol. 143,
Issue. 9,
Jamshed, Saqib
Kharbanda, Rohit
and
Dhiman, Amit Kumar
2022.
Study of flow through and around a pair of porous cylinders covering steady and unsteady regimes.
Physics of Fluids,
Vol. 34,
Issue. 10,
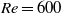 $\mathit{Re}= 600$ by direct numerical simulations. In the present work we verify that the global stability analysis provides reasonable estimation also when applied to experimental velocity fields measured in the wake past a porous circular cylinder at
$\mathit{Re}= 600$ by direct numerical simulations. In the present work we verify that the global stability analysis provides reasonable estimation also when applied to experimental velocity fields measured in the wake past a porous circular cylinder at 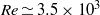 $\mathit{Re}\simeq 3. 5\ensuremath{\times} 1{0}^{3} $. Different intensities of continuous suction and blowing through the entire surface of the cylinder are considered. The global direct and adjoint stability modes, derived from the experimental data, are used to sort the random instantaneous snapshots of the velocity field in phase. The proposed method is remarkable, sorting the snapshots in phase with respect to the vortex shedding, allowing phase-averaged velocity fields to be extracted from the experimental database. The phase-averaged flow fields are analysed in order to study the effect of the transpiration on the kinematical characteristics of the large-scale wake vortices.
$\mathit{Re}\simeq 3. 5\ensuremath{\times} 1{0}^{3} $. Different intensities of continuous suction and blowing through the entire surface of the cylinder are considered. The global direct and adjoint stability modes, derived from the experimental data, are used to sort the random instantaneous snapshots of the velocity field in phase. The proposed method is remarkable, sorting the snapshots in phase with respect to the vortex shedding, allowing phase-averaged velocity fields to be extracted from the experimental database. The phase-averaged flow fields are analysed in order to study the effect of the transpiration on the kinematical characteristics of the large-scale wake vortices.