Published online by Cambridge University Press: 14 May 2019
Measurements of concentration fluctuations in a passive scalar plume released within a turbulent boundary layer are utilised to ascertain the scaling of concentration spectra. It is observed that the concentration spectra in a narrow meandering plume has a self-similar behaviour in both transverse (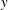 $y$) and vertical (
$y$) and vertical ( $z$, i.e. wall-normal) directions. Experimental data reveal self-similarity when the magnitude of concentration spectra is scaled by the local concentration variance whereas frequency is suitably scaled utilising the integral length scale of the streamwise velocity or the boundary layer thickness and the source velocity as length and velocity scales, respectively. Furthermore, our data show that at each frequency, the concentration energy is distributed across the
$z$, i.e. wall-normal) directions. Experimental data reveal self-similarity when the magnitude of concentration spectra is scaled by the local concentration variance whereas frequency is suitably scaled utilising the integral length scale of the streamwise velocity or the boundary layer thickness and the source velocity as length and velocity scales, respectively. Furthermore, our data show that at each frequency, the concentration energy is distributed across the 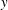 $y$ and
$y$ and  $z$ directions that is proportional to concentration variance at that location. These results are consistent with our non-dimensional analysis. Based on these observations, if the mean plume statistics are known, a model is proposed with which concentration spectrum at any position within the plume can be calculated using the spectrum at any another location as the input. The model is tested extensively for point-source plumes released at various heights and streamwise distances in a turbulent boundary layer, and is found to predict spectra at different
$z$ directions that is proportional to concentration variance at that location. These results are consistent with our non-dimensional analysis. Based on these observations, if the mean plume statistics are known, a model is proposed with which concentration spectrum at any position within the plume can be calculated using the spectrum at any another location as the input. The model is tested extensively for point-source plumes released at various heights and streamwise distances in a turbulent boundary layer, and is found to predict spectra at different  $y$ and
$y$ and  $z$ locations in close agreement with measurements.
$z$ locations in close agreement with measurements.