Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-05T11:31:17.209Z Has data issue: false hasContentIssue false
  • English
  • Français

Sedimentation of inertia-less prolate spheroids in homogenous isotropic turbulence with application to non-motile phytoplankton

Published online by Cambridge University Press:  13 October 2017

M. Niazi Ardekani Open the ORCID record for M. Niazi Ardekani [Opens in a new window] ,
G. Sardina Open the ORCID record for G. Sardina [Opens in a new window] ,
L. Brandt ,
L. Karp-Boss ,
R. N. Bearon  and
E. A. Variano
M. Niazi Ardekani*
Affiliation:
Linné Flow Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE-100 44 Stockholm, Sweden
G. Sardina
Affiliation:
Linné Flow Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE-100 44 Stockholm, Sweden Department of Mechanics and Maritime Sciences, Chalmers University of Technology, 412 96 Gothenburg, Sweden
L. Brandt
Affiliation:
Linné Flow Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE-100 44 Stockholm, Sweden
L. Karp-Boss
Affiliation:
School of Marine Sciences, University of Maine, Orono, ME 04469, USA
R. N. Bearon
Affiliation:
Department of Mathematical Sciences, University of Liverpool, Liverpool L69 7ZL, UK
E. A. Variano
Affiliation:
Department of Civil and Environmental Engineering, University of California, Berkeley, CA 94720, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

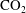Phytoplankton are the foundation of aquatic food webs. Through photosynthesis, phytoplankton draw down $\text{CO}_{2}$ at magnitudes equivalent to forests and other terrestrial plants and convert it to organic material that is then consumed by other planktonic organisms in higher trophic levels. Mechanisms that affect local concentrations and velocities are of primary significance to many encounter-based processes in the plankton, including prey–predator interactions, fertilization and aggregate formation. We report results from simulations of sinking phytoplankton, considered as elongated spheroids, in homogenous isotropic turbulence to answer the question of whether trajectories and velocities of sinking phytoplankton are altered by turbulence. We show in particular that settling spheroids with physical characteristics similar to those of diatoms weakly cluster and preferentially sample regions of downwelling flow, corresponding to an increase of the mean settling speed with respect to the mean settling speed in quiescent fluid. We explain how different parameters can affect the settling speed and what underlying mechanisms might be involved. Interestingly, we observe that the increase in the aspect ratio of the prolate spheroids can affect the clustering and the average settling speed of particles by two mechanisms: first is the effect of aspect ratio on the rotation rate of the particles, which saturates faster than the second mechanism of increasing drag anisotropy.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Isotropic turbulence Multiphase and Particle-laden Flows: Particle/fluid flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 831 , 25 November 2017 , pp. 655 - 674
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersson, H. I., Zhao, L. & Barri, M. 2012 Torque-coupling and particle–turbulence interactions. J. Fluid Mech. 696, 319–329.Google Scholar
Barton, A. D., Ward, B. A., Williams, R. G. & Follows, M. J. 2014 The impact of fine-scale turbulence on phytoplankton community structure. Limnol. Oceanogr. 4 (1), 34–49.CrossRefGoogle Scholar
Bec, J., Homann, H. & Ray, S. S. 2014 Gravity-driven enhancement of heavy particle clustering in turbulent flow. Phys. Rev. Lett. 112 (18), 184501.Google Scholar
Butler, J. E. & Shaqfeh, E. S. 2002 Dynamic simulations of the inhomogeneous sedimentation of rigid fibres. J. Fluid Mech. 468, 205–237.CrossRefGoogle Scholar
Byron, M., Einarsson, J., Gustavsson, K., Voth, G., Mehlig, B. & Variano, E. 2015 Shape-dependence of particle rotation in isotropic turbulence. Phys. Fluids 27 (3), 035101.Google Scholar
Chevillard, L. & Meneveau, C. 2013 Orientation dynamics of small, triaxial–ellipsoidal particles in isotropic turbulence. J. Fluid Mech. 737, 571–596.CrossRefGoogle Scholar
Clavano, W. R., Boss, E. & Karp-Boss, L. 2007 Inherent optical properties of non-spherical marine-like particles from theory to observation. Oceanogr. Mar. Biol. Annu. Rev. 45, 1–38.Google Scholar
Dahlkild, A. A. 2011 Finite wavelength selection for the linear instability of a suspension of settling spheroids. J. Fluid Mech. 689, 183–202.Google Scholar
Durham, W. M., Climent, E., Barry, M., De Lillo, F., Boffetta, G., Cencini, M. & Stocker, R. 2013 Turbulence drives microscale patches of motile phytoplankton. Nature Commun. 4, 2148.Google Scholar
Eppley, R. W., Holmes, R. W. & Strickland, J. D. H. 1967 Sinking rates of marine phytoplankton measured with a fluorometer. J. Exp. Marine Biol. Ecol. 1 (2), 191–208.Google Scholar
Gerbi, G. P., Trowbridge, J. H., Terray, E. A., Plueddemann, A. J & Kukulka, T. 2009 Observations of turbulence in the ocean surface boundary layer: energetics and transport. J. Phys. Oceanogr. 39 (5), 1077–1096.Google Scholar
Guazzelli, E. & Hinch, J. 2011 Fluctuations and instability in sedimentation. Annu. Rev. Fluid Mech. 43, 97–116.Google Scholar
Guazzelli, E. & Morris, J. F. 2011 A Physical Introduction to Suspension Dynamics, vol. 45. Cambridge University Press.Google Scholar
Gustavsson, K. & Tornberg, A. K. 2009 Gravity induced sedimentation of slender fibers. Phys. Fluids 21 (12), 123301.Google Scholar
Gustavsson, K., Vajedi, S. & Mehlig, B. 2014 Clustering of particles falling in a turbulent flow. Phys. Rev. Lett. 112 (21), 214501.Google Scholar
Herzhaft, B. & Guazzelli, E. 1999 Experimental study of the sedimentation of dilute and semi-dilute suspensions of fibres. J. Fluid Mech. 384, 133–158.CrossRefGoogle Scholar
Herzhaft, B., Guazzelli, E., Mackaplow, M. B. & Shaqfeh, E. S. 1996 Experimental investigation of the sedimentation of a dilute fiber suspension. Phys. Rev. Lett. 77 (2), 290.Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, vol. 102, pp. 161–179. The Royal Society.Google Scholar
Karp-Boss, L. & Boss, E. 2016 The elongated, the squat and the spherical: selective pressures for phytoplankton shape. In Aquatic Microbial Ecology and Biogeochemistry: A Dual Perspective, pp. 25–34. Springer.Google Scholar
Karp-Boss, L. & Jumars, P. A. 1998 Motion of diatom chains in steady shear flow. Limnol. Oceanogr. 43, 1767–1773.Google Scholar
Koch, D. L. & Shaqfeh, E. S. 1989 The instability of a dispersion of sedimenting spheroids. J. Fluid Mech. 209, 521–542.CrossRefGoogle Scholar
Lewis, W. M. 1976 Surface/volume ratio: implications for phytoplankton morphology. Science 192 (4242), 885–887.CrossRefGoogle ScholarPubMed
Mackaplow, M. B. & Shaqfeh, E. S. 1998 A numerical study of the sedimentation of fibre suspensions. J. Fluid Mech. 376, 149–182.Google Scholar
Malkiel, E., Alquaddoomi, O. & Katz, J. 1999 Measurements of plankton distribution in the ocean using submersible holography. Meas. Sci. Technol. 10 (12), 1142.Google Scholar
Mallier, R. & Maxey, M. 1991 The settling of nonspherical particles in a cellular flow field. Phys. Fluids A 3 (6), 1481–1494.Google Scholar
Marchioli, C., Fantoni, M. & Soldati, A. 2010 Orientation, distribution, and deposition of elongated, inertial fibers in turbulent channel flow. Phys. Fluids 22 (3), 033301.Google Scholar
Marchioli, C., Zhao, L. & Andersson, H. I. 2016 On the relative rotational motion between rigid fibers and fluid in turbulent channel flow. Phys. Fluids 28 (1), 013301.CrossRefGoogle Scholar
Margalef, R. 1978 Life-forms of phytoplankton as survival alternatives in an unstable environment. Oceanol. Acta 1 (4), 493–509.Google Scholar
Mitchell, J. G., Yamazaki, H., Seuront, L., Wolk, F. & Li, H. 2008 Phytoplankton patch patterns: seascape anatomy in a turbulent ocean. J. Mar. Syst. 69 (3), 247–253.CrossRefGoogle Scholar
Nguyen, H., Karp-Boss, L., Jumars, P. A & Fauci, L. 2011 Hydrodynamic effects of spines: a different spin. Limnol. Oceanogr. 1 (1), 110–119.Google Scholar
Ni, R., Kramel, S., Ouellette, N. T & Voth, G. A. 2015 Measurements of the coupling between the tumbling of rods and the velocity gradient tensor in turbulence. J. Fluid Mech. 766, 202–225.CrossRefGoogle Scholar
Olson, J. A. & Kerekes, R. J. 1998 The motion of fibres in turbulent flow. J. Fluid Mech. 377, 47–64.Google Scholar
Parsa, S., Calzavarini, E., Toschi, F. & Voth, G. A. 2012 Rotation rate of rods in turbulent fluid flow. Phys. Rev. Lett. 109 (13), 134501.Google Scholar
Parsa, S. & Voth, G. A. 2014 Inertial range scaling in rotations of long rods in turbulence. Phys. Rev. Lett. 112 (2), 024501.CrossRefGoogle ScholarPubMed
Pumir, A. & Wilkinson, M. 2011 Orientation statistics of small particles in turbulence. New J. Phys. 13 (9), 093030.Google Scholar
Reynolds, C. S. 1989 Physical determinants of phytoplankton succession. In Plankton Ecology, pp. 9–56. Springer.Google Scholar
Reynolds, C. S. & Irish, A. E. 1997 Modelling phytoplankton dynamics in lakes and reservoirs: the problem of in-situ growth rates. Hydrobiologia 349 (1–3), 5–17.Google Scholar
Rogallo, R. S.1981 Numerical experiments in homogeneous turbulence. NASA STI/Recon Tech. Rep. N 81, 31508.Google Scholar
Ruiz, J., Macías, D. & Peters, F. 2004 Turbulence increases the average settling velocity of phytoplankton cells. Proc. Natl Acad. Sci. USA 101 (51), 17720–17724.Google Scholar
Sardina, G., Picano, F., Brandt, L. & Caballero, R. 2015 Continuous growth of droplet size variance due to condensation in turbulent clouds. Phys. Rev. Lett. 115 (18), 184501.Google Scholar
Seuront, L., Schmitt, F. & Lagadeuc, Y. 2001 Turbulence intermittency, small-scale phytoplankton patchiness and encounter rates in plankton: where do we go from here? Deep-Sea Res. (I) 48 (5), 1199–1215.CrossRefGoogle Scholar
Shapiro, M. & Goldenberg, M. 1993 Deposition of glass fiber particles from turbulent air flow in a pipe. J. Aerosol Sci. 24 (1), 65–87.Google Scholar
Shin, H. & Maxey, M. R. 1997 Chaotic motion of nonspherical particles settling in a cellular flow field. Phys. Rev. E 56 (5), 5431.Google Scholar
Shin, M. & Koch, D. L. 2005 Rotational and translational dispersion of fibres in isotropic turbulent flows. J. Fluid Mech. 540, 143–173.Google Scholar
Siewert, C., Kunnen, R. P. J., Meinke, M. & Schröder, W. 2014 Orientation statistics and settling velocity of ellipsoids in decaying turbulence. Atmospheric Res. 142, 45–56.Google Scholar
Smayda, T. J. 1970 The suspension and sinking of phytoplankton in the sea. Ann. Rev. Oceanogr. Mar. Bioi. 8, 353–414.Google Scholar
Smyth, W. D. & Moum, J. N.2000 Ocean turbulence. Tech. Rep. College of Oceanic and Atmospheric Sciences, Oregon State University.Google Scholar
Sournia, A. 1982 Form and function in marine phytoplankton. Biol. Rev. 57 (3), 347–394.Google Scholar
Thorpe, S. A. 2007 An Introduction to Ocean Turbulence. Cambridge University Press.Google Scholar
Toschi, F. & Bodenschatz, E. 2009 Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41, 375–404.Google Scholar
Vincent, A. & Meneguzzi, M. 1994 The dynamics of vorticity tubes in homogeneous turbulence. J. Fluid Mech. 258, 245–254.Google Scholar
Voth, G. A. & Soldati, A. 2017 Anisotropic particles in turbulence. Annu. Rev. Fluid Mech. 49, 249–276.Google Scholar
Wang, L. P. & Maxey, M. R. 1993 Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 256, 27–68.CrossRefGoogle Scholar
Wang, L. P. & Stock, D. E. 1993 Dispersion of heavy particles by turbulent motion. J. Atmos. Sci. 50 (13), 1897–1913.Google Scholar
Young, A. M.2011 Quantifying diatom aspirations: mechanical properties of chain-forming species. PhD thesis, The University of Maine.Google Scholar
Zhan, C., Sardina, G., Lushi, E. & Brandt, L. 2014 Accumulation of motile elongated micro-organisms in turbulence. J. Fluid Mech. 739, 22–36.Google Scholar
Zhang, H., Ahmadi, G., Fan, F. G. & McLaughlin, J. B. 2001 Ellipsoidal particles transport and deposition in turbulent channel flows. Intl J. Multiphase Flow 27 (6), 971–1009.Google Scholar
Zhao, L., Challabotla, N. R., Andersson, H. I. & Variano, E. A. 2015 Rotation of nonspherical particles in turbulent channel flow. Phys. Rev. Lett. 115 (24), 244501.Google Scholar