Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-25T23:49:29.979Z Has data issue: false hasContentIssue false
  • English
  • Français

Scaling of the turbulent energy dissipation correlation function

Published online by Cambridge University Press:  27 March 2020

S. L. Tang Open the ORCID record for S. L. Tang [Opens in a new window] ,
R. A. Antonia ,
L. Djenidi Open the ORCID record for L. Djenidi [Opens in a new window]  and
Y. Zhou
S. L. Tang*
Affiliation:
Institute for Turbulence-Noise-Vibration Interaction and Control Harbin Institute of Technology, Shenzhen518055, PR China Digital Engineering Laboratory of Offshore Equipment, Shenzhen518055, PR China
R. A. Antonia
Affiliation:
School of Engineering, University of Newcastle, NSW 2308, Australia
L. Djenidi
Affiliation:
School of Engineering, University of Newcastle, NSW 2308, Australia
Y. Zhou
Affiliation:
Institute for Turbulence-Noise-Vibration Interaction and Control Harbin Institute of Technology, Shenzhen518055, PR China Digital Engineering Laboratory of Offshore Equipment, Shenzhen518055, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

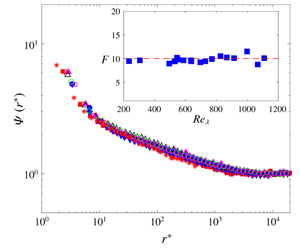
We examine the scaling of the two-point correlation function for $\unicode[STIX]{x1D716}$, the energy dissipation rate, over a range of values of the separation $r$ between the two points and the Taylor microscale Reynolds number $Re_{\unicode[STIX]{x1D706}}$. The correlation function is estimated from hot-wire measurements in grid turbulence, along the axes of wakes and jets, and along the centreline of a fully developed channel flow. When $Re_{\unicode[STIX]{x1D706}}$ exceeds a value of approximately 300, a condition which is achieved for both plane and circular jets, the correlation function collapses over nearly all values of $r$ when the normalization uses Kolmogorov scales. However, there is no collapse in either the power-law range or dissipative range when the normalization is on the integral (or external) length scale, which indicates that there is no self-similarity based on external scales. Although the maximum value of $Re_{\unicode[STIX]{x1D706}}$ is not much larger than $10^{3}$, the behaviour of the energy dissipation correlation function on the axes of plane and circular jets seems consistent with the first similarity hypothesis of Kolmogorov (Dokl. Akad. Nauk SSSR, vol. 30, 1941, pp. 299–303) but not with the revised phenomenology of Kolmogorov (J. Fluid Mech., vol. 13, 1962, pp. 82–85).

JFM classification

Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 891 , 25 May 2020 , A26
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Antonia, R. A. & Kawamura, H. 2009 Correlation between small-scale velocity and scalar fluctuations in a turbulent channel flow. J. Fluid Mech. 627, 1–32.CrossRefGoogle Scholar
Anselmet, F., Gagne, Y., Hopfinger, E. J. & Antonia, R. A. 1984 High-order velocity structure functions in turbulent shear flows. J. Fluid Mech. 140, 63–89.CrossRefGoogle Scholar
Antonia, R. A. & Burattini, P. 2006 Approach to the 4/5 law in homogeneous isotropic turbulence. J. Fluid Mech. 550, 175–184.CrossRefGoogle Scholar
Antonia, R. A., Djenidi, L. & Danaila, L. 2014 Collapse of the turbulent dissipation range on Kolmogorov scales. Phys. Fluids 26, 045105.CrossRefGoogle Scholar
Antonia, R. A., Djenidi, L., Danaila, L. & Tang, S. L. 2017 Small scale turbulence and the finite Reynolds number effect. Phys. Fluids 29 (2), 020715.CrossRefGoogle Scholar
Antonia, R. A., Phan-Thien, N. & Satyaprakash, B. R. 1981 Autocorrelation and spectrum of dissipation fluctuations in a turbulent jet. Phys. Fluids 24 (3), 554–555.CrossRefGoogle Scholar
Antonia, R. A., Satyaprakash, B. R. & Hussain, A. K. M. F. 1982 Statistics of fine-scale velocity in turbulent plane and circular jets. J. Fluid Mech. 119, 55–89.CrossRefGoogle Scholar
Antonia, R. A., Tang, S. L., Djenidi, L. & Danaila, L. 2015 Boundedness of the velocity derivative skewness in various turbulent flows. J. Fluid Mech. 781, 727–744.CrossRefGoogle Scholar
Antonia, R. A., Tang, S. L., Djenidi, L. & Zhou, Y. 2019 Finite Reynolds number effect and the 4/5 law. Phys. Rev. Fluids 4 (8), 084602.CrossRefGoogle Scholar
Antonia, R. A., Zhou, T. & Romano, G. P. 2002 Small-scale turbulence characteristics of two-dimensional bluff body wakes. J. Fluid Mech. 459, 67–92.CrossRefGoogle Scholar
Antonia, R. A., Zhou, T. & Zhu, Y. 1998 Three-component vorticity measurements in a turbulent grid flow. J. Fluid Mech. 374, 29–57.CrossRefGoogle Scholar
Bilger, R. W., Antonia, R. A. & Sreenivasan, K. R. 1976 Determination of intermittency from the probability density function of a passive scalar. Phys. Fluids 19 (10), 1471–1474.CrossRefGoogle Scholar
Boschung, J., Gauding, M., Hennig, F., Denker, D. & Pitsch, H. 2016 Finite Reynolds number corrections of the 4/5 law for decaying turbulence. Phys. Rev. Fluids 1, 064403.CrossRefGoogle Scholar
Browne, L. W., Antonia, R. A. & Shah, D. A. 1987 Turbulent energy dissipation in a wake. J. Fluid Mech. 179, 307–326.CrossRefGoogle Scholar
Burattini, P., Lavoie, P. & Antonia, R. 2005 On the normalized turbulent energy dissipation rate. Phys. Fluids 17, 098103.CrossRefGoogle Scholar
Cleve, J., Greiner, M., Pearson, B. R. & Sreenivasan, K. R. 2004 Intermittency exponent of the turbulent energy cascade. Phys. Rev. E 69, 066316.Google ScholarPubMed
Cleve, J., Greiner, M. & Sreenivasan, K. R. 2003 On the effects of surrogacy of energy dissipation in determining the intermittency exponent in fully developed turbulence. Eur. Phys. Lett. 61 (6), 756–761.CrossRefGoogle Scholar
Djenidi, L. & Antonia, R. A. 2012 A spectral chart method for estimating the mean turbulent kinetic energy dissipation rate. Exp. Fluids 53, 1005–1013.CrossRefGoogle Scholar
Djenidi, L. & Antonia, R. A. 2014 Transport equation for the mean turbulent energy dissipation rate in low-R 𝜆 grid turbulence. J. Fluid Mech. 747, 288–315.CrossRefGoogle Scholar
Djenidi, L., Antonia, R. A., Lefeuvre, N. & Lemay, J. 2016 Complete self-preservation on the axis of a turbulent round jet. J. Fluid Mech. 790, 57–70.CrossRefGoogle Scholar
Djenidi, L., Antonia, R. A. & Tang, S. L. 2019 Scale invariance in finite Reynolds number homogeneous isotropic turbulence. J. Fluid Mech. 864, 244–272.CrossRefGoogle Scholar
Djenidi, L., Lefeuvre, N., Kamruzzaman, M. & Antonia, R. A. 2017 On the normalized dissipation parameter c 𝜖 in decaying turbulence. J. Fluid Mech. 817, 61–79.CrossRefGoogle Scholar
Frisch, U., Sulem, P. L. & Nelkin, M. 1978 A simple dynamical model of intermittent fully developed turbulence. J. Fluid Mech. 87, 719–736.CrossRefGoogle Scholar
Goto, S. & Vassilicos, J. C. 2009 The dissipation rate coefficient of turbulence is not universal and depends on the internal stagnation point structure. Phys. Fluids 21 (3), 035104.CrossRefGoogle Scholar
Gurvich, A. S. & Yaglom, A. M. 1967 Breakdown of eddies and probability distributions for small-scale turbulence. Phys. Fluids 10 (9), S59–S65.CrossRefGoogle Scholar
Hosokawa, I., Oide, S. & Yamamoto, K. 1996 Isotropic turbulence: important differences between true dissipation rate and its one-dimensional surrogate. Phys. Rev. Lett. 77, 4548–4551.CrossRefGoogle ScholarPubMed
Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.CrossRefGoogle Scholar
Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2007 Small-scale statistics in high-resolution direct numerical simulation of turbulence: Reynolds number dependence of one-point velocity gradient statistics. J. Fluid Mech. 592, 335–366.CrossRefGoogle Scholar
Ishihara, T., Morishita, K., Yokokawa, M., Uno, A. & Kaneda, Y. 2016 Energy spectrum in high-resolution direct numerical simulations of turbulence. Phys. Rev. Fluids 1 (8), 082403.CrossRefGoogle Scholar
Iyer, K. P., Sreenivasan, K. R. & Yeung, P. K. 2017 Reynolds number scaling of velocity increments in isotropic turbulence. Phys. Rev. E 95 (2–1), 021101.Google ScholarPubMed
Kerr, R. M. 1985 Higher-order derivative correlations and the alignment of small-scale structures in isotropic numerical turbulence. J. Fluid Mech. 153, 31–58.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941a Local structure of turbulence in an incompressible fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299–303.Google Scholar
Kolmogorov, A. N. 1941b Dissipation of energy in the locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32, 19–21.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.CrossRefGoogle Scholar
Kuznetsov, V. R., Praskovsky, A. A. & Sabelnikov, V. A. 1992 Fine-scale turbulence structure of intermittent shear flows. J. Fluid Mech. 243, 595–622.CrossRefGoogle Scholar
Linkmann, M. 2018 Effects of helicity on dissipation in homogeneous box turbulence. J. Fluid Mech. 856, 79–102.CrossRefGoogle Scholar
Lundgren, T. S. 2003 Kolmogorov turbulence by matched asymptotic expansions. Phys. Fluids 15 (4), 1074–1081.CrossRefGoogle Scholar
McComb, W. D., Berera, A., Yoffe, S. R. & Linkmann, M. F. 2015 Energy transfer and dissipation in forced isotropic turbulence. Phys. Rev. E 91, 043013.Google ScholarPubMed
Mi, J., Xu, M. & Zhou, T. 2013 Reynolds number influence on statistical behaviors of turbulence in a circular free jet. Phys. Fluids 25, 075101.CrossRefGoogle Scholar
Monin, A. S & Yaglom, A. M. 1975 Statistical Fluid Dynamics, vol. 2. MIT.Google Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.CrossRefGoogle Scholar
Nelkin, M. 1981 Do the dissipation fluctuations in high Reynolds number turbulence define a universal exponent? Phys. Fluids 24 (3), 556–557.CrossRefGoogle Scholar
Nelkin, M. 2000 Resource letter TF-1: turbulence in fluids. Am. J. Phys. 68 (4), 310–318.CrossRefGoogle Scholar
Obukhov, A. M. 1962 Some specific features of atmospheric turbulence. J. Fluid Mech. 13 (1), 77–81.CrossRefGoogle Scholar
Pearson, B. R. & Antonia, R. A. 2001 Reynolds-number dependence of turbulent velocity and pressure increments. J. Fluid Mech. 444, 343–382.CrossRefGoogle Scholar
Praskovsky, A. & Oncley, S. 1994 Measurements of the Kolmogorov constant and intermittency exponent at very high Reynolds numbers. Phys. Fluids 6, 2886–2888.CrossRefGoogle Scholar
Qian, J. 1994 Skewness factor of turbulent velocity derivative. Acta Mech. Sin. 10, 12–15.Google Scholar
Qian, J. 1997 Inertial range and the finite Reynolds number effect of turbulence. Phys. Rev. E 55, 337–342.Google Scholar
Qian, J. 1998 Normal and anomalous scaling of turbulence. Phys. Rev. E 58, 7325–7329.Google Scholar
Shafi, H. S., Zhu, Y. & Antonia, R. A. 1997 Statistics of ∂u/∂y in a turbulent wake. Fluid Dyn. Res. 19 (3), 169183.Google Scholar
She, Z. S., Jackson, E. & Orszag, S. A. 1990 Intermittent vortex structures in homogeneous isotropic turbulence. Nature 344, 226–228.CrossRefGoogle Scholar
Sreenivasan, K. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.CrossRefGoogle Scholar
Sreenivasan, K. R. 1984 On the scaling of the turbulence energy dissipation rate. Phys. Fluids 27, 1048–1051.CrossRefGoogle Scholar
Sreenivasan, K. R. & Kailasnath, P. 1993 An update on the intermittency exponent in turbulence. Phys. Fluids 5 (2), 512–514.CrossRefGoogle Scholar
Stolovitzky, G., Meneveau, C. & Sreenivasan, K. R. 1998 Comment on ‘Isotropic turbulence: important differences between true dissipation rate and its one-dimensional surrogate’. Phys. Rev. Lett. 80, 3883–3883.CrossRefGoogle Scholar
Tang, S. L., Antonia, R. A., Djenidi, L., Abe, H., Zhou, T., Danaila, L. & Zhou, Y. 2015a Transport equation for the mean turbulent energy dissipation rate on the centreline of a fully developed channel flow. J. Fluid Mech. 777, 151–177.CrossRefGoogle Scholar
Tang, S. L., Antonia, R. A., Djenidi, L., Danaila, L. & Zhou, Y. 2017 Finite Reynolds number effect on the scaling range behaviour of turbulent longitudinal velocity structure functions. J. Fluid Mech. 820, 341–369.CrossRefGoogle Scholar
Tang, S. L., Antonia, R. A., Djenidi, L., Danaila, L. & Zhou, Y. 2018 Reappraisal of the velocity derivative flatness factor in various turbulent flows. J. Fluid Mech. 847, 244–265.CrossRefGoogle Scholar
Tang, S. L., Antonia, R. A., Djenidi, L. & Zhou, Y. 2015b Transport equation for the isotropic turbulent energy dissipation rate in the far-wake of a circular cylinder. J. Fluid Mech. 784, 109–129.CrossRefGoogle Scholar
Tang, S., Antonia, R. A., Djenidi, L. & Zhou, Y. 2019 Can small-scale turbulence approach a quasi-universal state? Phys. Rev. Fluids 4 (2), 024607.CrossRefGoogle Scholar
Taylor, G. I. 1935 Statistical theory of turbulence. Part I. Proc. R. Soc. Lond. A 151, 421–444.CrossRefGoogle Scholar
Tchoufag, J., Sagaut, P. & Cambon, C. 2012 Spectral approach to finite Reynolds number effects on Kolmogorov’s 4/5 law in isotropic turbulence. Phys. Fluids 24 (1), 015107.CrossRefGoogle Scholar
Tsinober, A., Kit, E. & Dracos, T. 1992 Experimental investigation of the field of velocity gradients in turbulent flows. J. Fluid Mech. 242, 169–192.CrossRefGoogle Scholar
Vassilicos, J. C. 2015 Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 47, 95–114.CrossRefGoogle Scholar
Xu, G., Antonia, R. A. & Rajagopalan, S. 2001 Sweeping decorrelation hypothesis in a turbulent round jet. Fluid Dyn. Res. 28 (5), 311–321.CrossRefGoogle Scholar
Yaglom, A. M. 1966 Effect of fluctuations in energy dissipation rate on the form of turbulence characteristics in the inertial subrange. Dokl. Akad. Nauk SSSR 166, 49–52.Google Scholar
Zhou, T. & Antonia, R. A. 2000 Reynolds number dependence of the small-scale structure of grid turbulence. J. Fluid Mech. 406, 81–107.CrossRefGoogle Scholar
Zhou, T., Antonia, R. A. & Chua, L. P. 2005 Flow and Reynolds number dependencies of one-dimensional vorticity fluctuations. J. Turbul. 6, N28.Google Scholar