Published online by Cambridge University Press: 19 December 2018
We conducted direct numerical simulations of turbulent flow over three-dimensional sinusoidal roughness in a channel. A passive scalar is present in the flow with Prandtl number 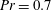 $Pr=0.7$, to study heat transfer by forced convection over this rough surface. The minimal-span channel is used to circumvent the high cost of simulating high-Reynolds-number flows, which enables a range of rough surfaces to be efficiently simulated. The near-wall temperature profile in the minimal-span channel agrees well with that of the conventional full-span channel, indicating that it can be readily used for heat-transfer studies at a much reduced cost compared to conventional direct numerical simulation. As the roughness Reynolds number,
$Pr=0.7$, to study heat transfer by forced convection over this rough surface. The minimal-span channel is used to circumvent the high cost of simulating high-Reynolds-number flows, which enables a range of rough surfaces to be efficiently simulated. The near-wall temperature profile in the minimal-span channel agrees well with that of the conventional full-span channel, indicating that it can be readily used for heat-transfer studies at a much reduced cost compared to conventional direct numerical simulation. As the roughness Reynolds number, 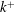 $k^{+}$, is increased, the Hama roughness function,
$k^{+}$, is increased, the Hama roughness function, 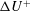 $\unicode[STIX]{x0394}U^{+}$, increases in the transitionally rough regime before tending towards the fully rough asymptote of
$\unicode[STIX]{x0394}U^{+}$, increases in the transitionally rough regime before tending towards the fully rough asymptote of 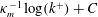 $\unicode[STIX]{x1D705}_{m}^{-1}\log (k^{+})+C$, where
$\unicode[STIX]{x1D705}_{m}^{-1}\log (k^{+})+C$, where 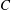 $C$ is a constant that depends on the particular roughness geometry and
$C$ is a constant that depends on the particular roughness geometry and 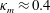 $\unicode[STIX]{x1D705}_{m}\approx 0.4$ is the von Kármán constant. In this fully rough regime, the skin-friction coefficient is constant with bulk Reynolds number,
$\unicode[STIX]{x1D705}_{m}\approx 0.4$ is the von Kármán constant. In this fully rough regime, the skin-friction coefficient is constant with bulk Reynolds number, 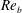 $Re_{b}$. Meanwhile, the temperature difference between smooth- and rough-wall flows,
$Re_{b}$. Meanwhile, the temperature difference between smooth- and rough-wall flows, 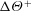 $\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}^{+}$, appears to tend towards a constant value,
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}^{+}$, appears to tend towards a constant value, 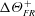 $\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}_{FR}^{+}$. This corresponds to the Stanton number (the temperature analogue of the skin-friction coefficient) monotonically decreasing with
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}_{FR}^{+}$. This corresponds to the Stanton number (the temperature analogue of the skin-friction coefficient) monotonically decreasing with 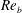 $Re_{b}$ in the fully rough regime. Using shifted logarithmic velocity and temperature profiles, the heat-transfer law as described by the Stanton number in the fully rough regime can be derived once both the equivalent sand-grain roughness
$Re_{b}$ in the fully rough regime. Using shifted logarithmic velocity and temperature profiles, the heat-transfer law as described by the Stanton number in the fully rough regime can be derived once both the equivalent sand-grain roughness 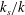 $k_{s}/k$ and the temperature difference
$k_{s}/k$ and the temperature difference 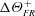 $\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}_{FR}^{+}$ are known. In meteorology, this corresponds to the ratio of momentum and heat-transfer roughness lengths,
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}_{FR}^{+}$ are known. In meteorology, this corresponds to the ratio of momentum and heat-transfer roughness lengths, 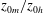 $z_{0m}/z_{0h}$, being linearly proportional to the inner-normalised momentum roughness length,
$z_{0m}/z_{0h}$, being linearly proportional to the inner-normalised momentum roughness length, 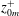 $z_{0m}^{+}$, where the constant of proportionality is related to
$z_{0m}^{+}$, where the constant of proportionality is related to 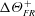 $\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}_{FR}^{+}$. While Reynolds analogy, or similarity between momentum and heat transfer, breaks down for the bulk skin-friction and heat-transfer coefficients, similar distribution patterns between the heat flux and viscous component of the wall shear stress are observed. Instantaneous visualisations of the temperature field show a thin thermal diffusive sublayer following the roughness geometry in the fully rough regime, resembling the viscous sublayer of a contorted smooth wall.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}_{FR}^{+}$. While Reynolds analogy, or similarity between momentum and heat transfer, breaks down for the bulk skin-friction and heat-transfer coefficients, similar distribution patterns between the heat flux and viscous component of the wall shear stress are observed. Instantaneous visualisations of the temperature field show a thin thermal diffusive sublayer following the roughness geometry in the fully rough regime, resembling the viscous sublayer of a contorted smooth wall.