Hostname: page-component-848d4c4894-89wxm Total loading time: 0 Render date: 2024-07-07T17:06:40.514Z Has data issue: false hasContentIssue false
  • English
  • Français

Rotating thermal convection in liquid gallium: multi-modal flow, absent steady columns

Published online by Cambridge University Press:  10 May 2018

Jonathan M. Aurnou Open the ORCID record for Jonathan M. Aurnou [Opens in a new window] ,
Vincent Bertin ,
Alexander M. Grannan ,
Susanne Horn Open the ORCID record for Susanne Horn [Opens in a new window]  and
Tobias Vogt
Jonathan M. Aurnou*
Affiliation:
Department of Earth, Planetary, and Space Sciences, University of California, Los Angeles, CA 90095, USA
Vincent Bertin
Affiliation:
Department of Earth, Planetary, and Space Sciences, University of California, Los Angeles, CA 90095, USA Department of Physics, École Normale Supérieure, Paris, France
Alexander M. Grannan
Affiliation:
Department of Earth, Planetary, and Space Sciences, University of California, Los Angeles, CA 90095, USA
Susanne Horn
Affiliation:
Department of Earth, Planetary, and Space Sciences, University of California, Los Angeles, CA 90095, USA
Tobias Vogt
Affiliation:
Institute of Fluid Dynamics, Helmholtz-Zentrum Dresden-Rossendorf, PO Box 510119, 01314 Dresden, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

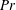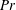Earth’s magnetic field is generated by convective motions in its liquid metal core. In this fluid, the heat diffuses significantly more than momentum, and thus the Prandtl number $Pr$ is well below unity. The thermally driven convective flow dynamics of liquid metals are very different from moderate- $Pr$ fluids, such as water and those used in current dynamo simulations. In order to characterise rapidly rotating thermal convection in low- 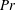$Pr$ number fluids, we have performed laboratory experiments in a cylinder of aspect ratio 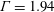$\unicode[STIX]{x1D6E4}=1.94$ using liquid gallium ( 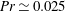$Pr\simeq 0.025$ ) as the working fluid. The Ekman number varies from 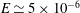$E\simeq 5\times 10^{-6}$ to 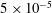$5\times 10^{-5}$ and the Rayleigh number varies from 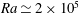$Ra\simeq 2\times 10^{5}$ to 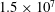$1.5\times 10^{7}$ . Using spectral analysis stemming from point-wise temperature measurements within the fluid and measurements of the Nusselt number 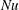$Nu$ , we characterise the different styles of low- 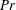$Pr$ rotating convective flow. The convection threshold is first overcome in the form of container-scale inertial oscillatory modes. At stronger forcing, sidewall-attached modes are identified for the first time in liquid metal laboratory experiments. These wall modes coexist with the bulk oscillatory modes. At $Ra$ well below the values where steady rotating columnar convection occurs, the bulk flow becomes turbulent. 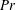Our results imply that rotating convective flows in liquid metals do not develop in the form of quasisteady columns, as in moderate- $Pr$ fluids, but in the form of oscillatory convective motions. Thus, thermally driven flows in low- 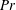$Pr$ geophysical and astrophysical fluids can differ substantively from those occurring in 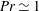$Pr\simeq 1$ models. Furthermore, our experimental results show that relatively low-frequency wall modes are an essential dynamical component of rapidly rotating convection in liquid metals.

JFM classification

Geophysical and Geological Flows: Geodynamo Geophysical and Geological Flows: Rotating flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 846 , 10 July 2018 , pp. 846 - 876
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G. 2000 Effect of sidewall conductance on heat-transport measurements for turbulent Rayleigh–Bénard convection. Phys. Rev. E 63 (1), 015303.Google ScholarPubMed
Andrade, E. N. da C. 1934 LVIII. A theory of the viscosity of liquids. Part II. The London, Edinburgh, and Dublin. Phil. Mag. J. Sci. 17 (113), 698–732.CrossRefGoogle Scholar
Assael, M. J., Armyra, I. J., Brillo, J., Stankus, S. V., Wu, J. & Wakeham, W. A. 2012 Reference data for the density and viscosity of liquid cadmium, cobalt, gallium, indium, mercury, silicon, thallium, and zinc. J. Phys. Chem. Ref. Data 41 (3), 033101.CrossRefGoogle Scholar
Aubert, J., Aurnou, J. M. & Wicht, J. 2008 The magnetic structure of convection-driven numerical dynamos. Geophys. J. Intl 172, 945–956.CrossRefGoogle Scholar
Aujogue, K., Pothérat, A., Sreenivasan, B. & Debray, F. 2018 Experimental study of the convection in a rotating tangent cylinder. J. Fluid Mech. 843, 355–381.CrossRefGoogle Scholar
Aurnou, J. M., Andreadis, S., Zhu, L. & Olson, P. 2003 Experiments on convection in Earth’s core tangent cylinder. Earth Planet. Sci. Lett. 212, 119–134.CrossRefGoogle Scholar
Aurnou, J. M., Calkins, M. A., Cheng, J. S., Julien, K., King, E. M., Nieves, D., Soderlund, K. M. & Stellmach, S. 2015 Rotating convective turbulence in Earth and planetary cores. Phys. Earth Planet. Inter 246, 52–71.CrossRefGoogle Scholar
Aurnou, J. M., Heimpel, M. H., Allen, L., King, E. M. & Wicht, J. 2008 Convective heat transfer and the pattern of thermal emission on the gas giants. Geophys. J. Intl 173, 793–801.CrossRefGoogle Scholar
Aurnou, J. M. & King, E. M. 2017 The cross-over to magnetostrophic convection in planetary dynamo systems. Proc. R. Soc. Lond. A 473, 20160731.Google ScholarPubMed
Aurnou, J. M. & Olson, P. 2001 Experiments on Rayleigh–Bénard convection, magnetoconvection, and rotating magnetoconvection in liquid gallium. J. Fluid Mech. 430, 283–307.CrossRefGoogle Scholar
Bailon-Cuba, J., Emran, M. S. & Schumacher, J. 2010 Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 655, 152–173.CrossRefGoogle Scholar
Bajaj, K. M. S., Ahlers, G. & Pesch, W. 2002 Rayleigh–Bénard convection with rotation at small Prandtl numbers. Phys. Rev. E 65 (5), 056309.Google ScholarPubMed
Brandes, E. A. & Brook, G. B.(Eds) 1992 Smithells Metals Reference Book, 7th edn. Butterworth-Heinemann.Google Scholar
Braunsfurth, M. G., Skeldon, A. C., Juel, A., Mullin, T. & Riley, D. S. 1997 Free convection in liquid gallium. J. Fluid Mech. 342, 295–314.CrossRefGoogle Scholar
Brito, D., Aurnou, J. M. & Cardin, P. 2004 Turbulent viscosity measurements relevant to planetary core-mantle dynamics. PEPI 141 (1), 3–8.Google Scholar
Brito, D., Nataf, H.-C., Cardin, P., Aubert, J. & Masson, J.-P. 2001 Ultrasonic Doppler velocimetry in liquid gallium. Exp. Fluids 31 (6), 653–663.CrossRefGoogle Scholar
Buffett, B. A., Huppert, H. E., Lister, J. R. & Woods, A. W. 1996 On the thermal evolution of the Earth’s core. J. Geophys. Res. 101 (B4), 7989–8006.CrossRefGoogle Scholar
Busse, F. H. 1970 Thermal instabilities in rapidly rotating systems. J. Fluid Mech. 44, 441–460.CrossRefGoogle Scholar
Busse, F. H. & Simitev, R. D. 2006 Parameter dependences of convection-driven dynamos in rotating spherical fluid shells. Geophys. Astrophys. Fluid Dyn. 100 (4–5), 341–361.CrossRefGoogle Scholar
Calkins, M. A. 2017 Quasi-geostrophic dynamo theory. Phys. Earth Planet. Inter. 266, 54–59.CrossRefGoogle Scholar
Calkins, M. A., Aurnou, J. M., Eldredge, J. D. & Julien, K. 2012 The influence of fluid properties on the morphology of core turbulence and the geomagnetic field. Earth Planet. Sci. Lett. 359–360, 55–60.CrossRefGoogle Scholar
Calkins, M. A., Julien, K., Tobias, S. & Aurnou, J. M. 2015 A multiscale dynamo model driven by quasi-geostrophic convection. J. Fluid Mech. 780, 143–166.CrossRefGoogle Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Cheng, J. S. & Aurnou, J. M. 2016 Tests of diffusion-free scaling behaviors in numerical dynamo datasets. Earth Planet. Sci. Lett. 436, 121–129.CrossRefGoogle Scholar
Cheng, J. S., Stellmach, S., Ribeiro, A., Grannan, A., King, E. M. & Aurnou, J. M. 2015 Laboratory-numerical models of rapidly rotating convection in planetary cores. Geophys. J. Intl 201, 1–17.CrossRefGoogle Scholar
Chiffaudel, A., Fauve, S. & Perrin, B. 1987 Viscous and inertial convection at low Prandtl number: experimental study. Europhys. Lett. 4, 555–560.CrossRefGoogle Scholar
Christensen, U. R. 2011 Geodynamo models: tools for understanding properties of Earth’s magnetic field. Phys. Earth Planet. Inter. 187, 157–169.CrossRefGoogle Scholar
Clune, T. & Knobloch, E. 1993 Pattern selection in rotating convection with experimental boundary conditions. Phys. Rev. E 47 (4), 2536–2550.Google ScholarPubMed
Curbelo, J., Lopez, J. M., Mancho, A. M. & Marques, F. 2014 Confined rotating convection with large Prandtl number: centrifugal effects on wall modes. Phys. Rev. E 89, 013019.Google ScholarPubMed
Davies, C., Pozzo, M., Gubbins, D. & Alfé, D. 2015 Constraints from material properties on the dynamics and evolution of Earth’s core. Nat. Geosci. 8, 678–685.CrossRefGoogle Scholar
Emran, M. S. & Schumacher, J. 2015 Large-scale mean patterns in turbulent convection. J. Fluid. Mech. 776, 96–108.CrossRefGoogle Scholar
Favier, B., Silvers, L. J. & Proctor, M. R. E. 2014 Inverse cascade and symmetry breaking in rapidly rotating Boussinesq convection. Phys. Fluids 26, 096605.CrossRefGoogle Scholar
Featherstone, N. A. & Miesch, M. S. 2015 Meridional circulation in solar and stellar convection zones. Astrophys. J. 804 (1), 67.CrossRefGoogle Scholar
Finlay, C. C. & Jackson, A. 2003 Equatorially dominated magnetic field change at the surface of Earth’s core. Science 300, 2084–2086.CrossRefGoogle ScholarPubMed
Gastine, T., Wicht, J. & Aubert, J. 2016 Scaling regimes in spherical shell rotating convection. J. Fluid Mech. 808, 690–732.CrossRefGoogle Scholar
Gastine, T., Wicht, J. & Aurnou, J. M. 2013 Zonal flow regimes in rotating anelastic spherical shells: an application to giant planets. Icarus 225 (1), 156–172.CrossRefGoogle Scholar
Genrikh, V. N., Kaplun, A. B. & Solovev, A. N.1972 Study of liquid viscosity by means of vibration method. Tech. Rep. DTIC Document.Google Scholar
Gillet, N., Brito, D., Jault, D. & Nataf, H.-C. 2007 Experimental and numerical studies of convection in a rapidly rotating spherical shell. J. Fluid Mech. 580, 83–121.CrossRefGoogle Scholar
Glatzmaier, G. A. & Roberts, P. H. 1995 A three-dimensional self-consistent computer simulation of a geomagnetic field reversal. Nature 377, 203–209.CrossRefGoogle Scholar
Goldstein, H. F., Knobloch, E., Mercader, I. & Net, M. 1993 Convection in a rotating cylinder. Part 1. Linear theory for moderate Prandtl numbers. J. Fluid Mech. 248, 583–604.CrossRefGoogle Scholar
Goldstein, H. F., Knobloch, E., Mercader, I. & Net, M. 1994 Convection in a rotating cylinder. Part 2. Linear theory for low Prandtl numbers. J. Fluid. Mech. 262, 293–324.CrossRefGoogle Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Greenspan, H. P. 1969 On the non-linear interaction of inertial modes. J. Fluid Mech. 36, 257–264.CrossRefGoogle Scholar
Greenspan, H. P. & Howard, L. N. 1963 On a time-dependent motion of a rotating fluid. J. Fluid Mech. 17 (3), 385–404.CrossRefGoogle Scholar
Grooms, I., Julien, K., Weiss, J. B. & Knobloch, E. 2010 Model of convective Taylor columns in rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 104, 224501.CrossRefGoogle ScholarPubMed
Grosse, A. V. 1961 The viscosity of liquid metals and an empirical relationship between their activation energy of viscosity and their melting points. J. Inorg. Nucl. Chem. 23 (3–4), 333–339.CrossRefGoogle Scholar
Gubbins, D. 2001 The Rayleigh number for convection in the Earth’s core. Phys. Earth Planet. Intl 128, 3–12.CrossRefGoogle Scholar
Guervilly, C. & Cardin, P. 2016 Subcritical convection of liquid metals in a rotating sphere using a quasi-geostrophic model. J. Fluid Mech. 808, 61–89.CrossRefGoogle Scholar
Herrmann, J. & Busse, F. H. 1993 Asymptotic theory of wall-attached convection in a rotating fluid layer. J. Fluid Mech. 255, 183–194.CrossRefGoogle Scholar
Horn, S. & Schmid, P. J. 2017 Prograde, retrograde, and oscillatory modes in rotating Rayleigh–Bénard convection. J. Fluid Mech. 831, 182–211.CrossRefGoogle Scholar
Horn, S. & Shishkina, O. 2014 Rotating non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water. Phys. Fluids. 26, 055111.CrossRefGoogle Scholar
Horn, S. & Shishkina, O. 2015 Toroidal and poloidal energy in rotating Rayleigh–Bénard convection. J. Fluid Mech. 762, 232–255.CrossRefGoogle Scholar
Huguet, L., Van Orman, J., Hauck, S.A. II & Willard, M. A. 2018 Earth’s inner core nucleation paradox. Earth Planet. Sci. Lett. 487, 9–20.CrossRefGoogle Scholar
Iida, T., Guthrie, R. & Tripathi, N. 2006 A model for accurate predictions of self-diffusivities in liquid metals, semimetals, and semiconductors. Metall. Mater. Trans. B 37 (4), 559–564.CrossRefGoogle Scholar
Iida, T., Morita, Z. & Takeuchi, S. 1975 Viscosity measurements of pure liquid metals by the capillary method. J. Japan Inst. Metals 39.11, 1169–1175.CrossRefGoogle Scholar
Jaupart, E. & Buffett, B. A. 2017 Generation of MAC waves by convection in Earth’s core. Geophys. J. Intl 209, 1326–1336.CrossRefGoogle Scholar
Jones, C. A. 2011 Planetary magnetic fields and fluid dynamos. Annu. Rev. Fluid Mech. 43, 583–614.CrossRefGoogle Scholar
Julien, K. & Knobloch, E. 1998 Strongly nonlinear convection cells in a rapidly rotating fluid layer: the tilted f-plane. J. Fluid Mech. 360, 141–178.CrossRefGoogle Scholar
Julien, K., Knobloch, E., Rubio, A. M. & Vasil, G. M. 2012a Heat transport in low-Rossby-number Rayleigh–Bénard convection. Phys. Rev. Lett. 109 (25), 254503.CrossRefGoogle ScholarPubMed
Julien, K., Knobloch, E. & Werne, J. 1999 Reduced equations for rotationally constrained convection. In Turbulence and Shear Flows, I (ed. Banerjee, S. & Eaton, J. K.), pp. 101–106. Begell House.Google Scholar
Julien, K., Legg, S., McWilliams, J. & Werne, J. 1996 Rapidly rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 322, 243–273.CrossRefGoogle Scholar
Julien, K., Rubio, A. M., Grooms, I. & Knobloch, E. 2012b Statistical and physical balances in low Rossby number Rayleigh–Bénard convection. Geophys. Astrophys. Fluid Dyn. 106 (4–5), 392–428.CrossRefGoogle Scholar
Kaplan, E. J., Schaeffer, N., Vidal, J. & Cardin, P. 2017 Subcritical thermal convection of liquid metals in a rapidly rotating sphere. Phys. Rev. Lett. 119, 094501.CrossRefGoogle Scholar
Kek, V. & Müller, U. 1993 Low Prandtl number convection in layers heated from below. Intl J. Heat Mass Transfer 36, 2795–2804.CrossRefGoogle Scholar
King, E. M. & Aurnou, J. M. 2012 Thermal evidence for Taylor columns in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. E 85, 016313.Google ScholarPubMed
King, E. M. & Aurnou, J. M. 2013 Turbulent convection in liquid metal with and without rotation. Proc. Natl Acad. Sci. USA 110, 6688–6693.CrossRefGoogle ScholarPubMed
King, E. M. & Aurnou, J. M. 2015 Magnetostrophic balance as the optimal state for turbulent magnetoconvection. Proc. Natl Acad. Sci. USA 112, 990–994.CrossRefGoogle ScholarPubMed
King, E. M., Soderlund, K. M., Christensen, U. R., Wicht, J. & Aurnou, J. M. 2010 Convective heat transfer in planetary dynamo models. Geochem. Geophys. Geosyst. 11 (6), Q06016.CrossRefGoogle Scholar
King, E. M., Stellmach, S. & Aurnou, J. M. 2012 Heat transfer by rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 691, 568–582.CrossRefGoogle Scholar
Liao, X., Zhang, K. & Chang, Y. 2006 On boundary-layer convection in a rotating fluid layer. J. Fluid Mech. 549, 375–384.CrossRefGoogle Scholar
Mabuchi, J., Masada, Y. & Kageyama, A. 2015 Differential rotation in magnetized and non-magnetized stars. Astrophys. J. 806 (1), 10.CrossRefGoogle Scholar
Nataf, H.-C. & Schaeffer, N. 2015 Turbulence in the Core. In Treatise on Geophysics, 2nd edn. vol. 8, chap. 6, pp. 161–181. Elsevier.CrossRefGoogle Scholar
Okada, K. & Ozoe, H. 1992 Experimental heat transfer rates of natural convection of molten gallium suppressed under an external magnetic field in either the x, y, or z direction. Trans. ASME J. Heat Transfer 114, 107–114.CrossRefGoogle Scholar
O’Rourke, J. & Stevenson, D. J. 2016 Powering Earth’s dynamo with magnesium precipitation from the core. Nature 529, 387–389.CrossRefGoogle ScholarPubMed
Plumley, M., Julien, K., Marti, P. & Stellmach, S. 2016 The effects of Ekman pumping on quasi-geostrophic Raleigh–Bénard convection. J. Fluid Mech. 803, 51–71.CrossRefGoogle Scholar
Predel, B. & Arpshofen, I. 1968 Viskosimetrische Untersuchungen zum Schmelzprozeß von Metallen am Beispiel des Galliums und der intermetallischen Verbindung Hg5 Tl2 . Z. Naturforsch. A 23 (12), 2052–2062.CrossRefGoogle Scholar
Roberts, P. H. & Aurnou, J. M. 2012 On the theory of core-mantle coupling. Geophys. Astrophys. Fluid Dyn. 106 (2), 157–230.CrossRefGoogle Scholar
Roberts, P. H. & King, E. M. 2013 On the genesis of the Earth’s magnetism. Rep. Prog. Phys. 76, 096801.CrossRefGoogle ScholarPubMed
Rossby, H. T. 1969 A study of Bénard convection with and without rotation. J. Fluid Mech. 36 (2), 309–335.CrossRefGoogle Scholar
Schaeffer, N., Jault, D., Nataf, H.-C. & Fournier, A. 2017 Turbulent geodynamo simulations: a leap towards Earth’s core. Geophys. J. Intl 211, 1–29.CrossRefGoogle Scholar
Scheel, J. D. & Schumacher, J. 2016 Global and local statistics in turbulent convection at low Prandtl numbers. J. Fluid Mech. 802, 147–173.CrossRefGoogle Scholar
Simitev, R. & Busse, F. H. 2005 Prandtl-number dependence of convection-driven dynamos in rotating spherical fluid shells. J. Fluid Mech. 532, 365–388.CrossRefGoogle Scholar
Soderlund, K. M., King, E. M. & Aurnou, J. M. 2012 The influence of magnetic fields in planetary dynamo models. Earth Planet. Sci. Lett. 333–334, 9–20.CrossRefGoogle Scholar
Soderlund, K. M., Schmidt, B. E., Wicht, J. & Blankenship, D. D. 2014 Ocean-driven heating of Europa’s icy shell at low latitudes. Nature Geosc. 7 (1), 16–19.CrossRefGoogle Scholar
Soderlund, K. M., Sheyko, A., King, E. M. & Aurnou, J. M. 2015 The competition between Lorentz and Coriolis forces in planetary dynamos. Prog. Earth Planet. Sci. 2, 24.CrossRefGoogle Scholar
Spells, K. E. 1936 The determination of the viscosity of liquid gallium over an extended range of temperature. Proc. Phys. Soc. 48 (2), 299–311.CrossRefGoogle Scholar
Sprague, M., Julien, K., Knobloch, E. & Werne, J. 2006 Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech. 551, 141–174.CrossRefGoogle Scholar
Sreenivasan, B. 2010 Modelling the geodynamo: progress and challenges. Curr. Sci. 99, 1739–1749.Google Scholar
Sreenivasan, B. & Jones, C. A. 2006 Azimuthal winds, convection and dynamo action in the polar regions of planetary cores. Geophys. Astrophys. Fluid Dyn. 100, 319–339.CrossRefGoogle Scholar
Stellmach, S., Lischper, M., Julien, K., Vasil, G., Cheng, J. S., Ribeiro, A., King, E. M. & Aurnou, J. M. 2014 Approaching the asymptotic regime of rapidly rotating convection: boundary layers versus interior dynamics. Phys. Rev. Lett. 113, 254501.CrossRefGoogle ScholarPubMed
Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2013 Heat transport and flow structure in rotating Rayleigh–Bénard convection. Eur. J. Mech. (B/Fluids) 40, 41–49.CrossRefGoogle Scholar
Tarduno, J., Cottrell, R. D., Davis, W. J. & Nimmo, F. 2015 A Hadean to Paleoarchean geodynamo recorded by single zircon crystals. Science 349, 521–524.CrossRefGoogle ScholarPubMed
Vogt, T., Grants, I., Eckert, S. & Gerbeth, G. 2013 Spin-up of a magnetically driven tornado-like vortex. J. Fluid Mech. 736, 641–662.CrossRefGoogle Scholar
Vogt, T., Grants, I., Räbiger, D., Eckert, S. & Gerbeth, G. 2012 On the formation of Taylor–Görtler vortices in RMF-driven spin-up flows. Exp. Fluids 52 (1), 1–10.CrossRefGoogle Scholar
Vogt, T., Räbiger, D. & Eckert, S. 2014 Inertial wave dynamics in a rotating liquid metal. J. Fluid Mech. 753, 472–498.CrossRefGoogle Scholar
Warn-Varnas, A., Fowlis, W. W., Piacsek, S. & Lee, S. M. 1978 Numerical solutions and laser-Doppler measurements of spin-up. J. Fluid Mech. 85 (4), 609–639.CrossRefGoogle Scholar
Xu, Q., Oudalov, N., Guo, Q., Jaeger, H. & Brown, E. 2012 Effect of oxidation on the mechanical properties of liquid gallium and eutectic gallium-indium. Phys. Fluids 24, 063101.CrossRefGoogle Scholar
Yadav, R., Gastine, T., Christensen, U. R., Wolk, S. J. & Poppenhaeger, K. 2016a Approaching a realistic force balance in geodynamo simulations. Proc. Natl Acad. Sci. USA 113 (40), 12065–12070.CrossRefGoogle ScholarPubMed
Yadav, R. K., Gastine, T., Christensen, U. R., Duarte, L. D. V. & Reiners, A. 2016b Effect of shear and magnetic field on the heat-transfer efficiency of convection in rotating spherical shells. Geophys. J. Intl 204 (2), 1120–1133.CrossRefGoogle Scholar
Zhang, K. 1994 On coupling between the Poincaré equation and the heat equation. J. Fluid Mech. 268, 211–229.CrossRefGoogle Scholar
Zhang, K. 1995 On coupling between the Poincaré equation and the heat equation: non-slip boundary condition. J. Fluid Mech. 284, 239–256.CrossRefGoogle Scholar
Zhang, K. & Liao, X. 2009 The onset of convection in rotating circular cylinders with experimental boundary conditions. J. Fluid Mech. 622, 63–73.CrossRefGoogle Scholar
Zhang, K. & Liao, X. 2017 Theory and Modeling of Rotating Fluids: Convection, Inertial Waves and Precession. Cambridge University Press.CrossRefGoogle Scholar
Zhang, K. & Schubert, G. 2000 Magnetohydrodynamics in rapidly rotating spherical systems. Annu. Rev. Fluid Mech. 32 (1), 409–443.CrossRefGoogle Scholar
Zhong, F., Ecke, R. E. & Steinberg, V. 1993 Rotating Rayleigh–Bénard convection: asymmetric modes and vortex states. J. Fluid Mech. 249, 135–159.CrossRefGoogle Scholar
Zhong, F., Ecke, R. E. & Steinberg, V. 1991 Asymmetric modes and the transition to vortex structures in rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 67 (18), 2473–2476.CrossRefGoogle ScholarPubMed
Zhong, J.-Q., Stevens, R. J. A. M., Clercx, H. J. H., Verzicco, R., Lohse, D. & Ahlers, G. 2009 Prandtl-, Rayleigh-, and Rossby-number dependence of heat transport in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 102, 044502.Google ScholarPubMed