Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-22T17:53:28.677Z Has data issue: false hasContentIssue false
  • English
  • Français

Reynolds number scaling of inertial particle statistics in turbulent channel flows

Published online by Cambridge University Press:  07 October 2014

Matteo Bernardini
Matteo Bernardini*
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Università di Roma ‘La Sapienza’, Via Eudossiana 18, 00184 Roma, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

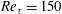The effect of the Reynolds number on the behaviour of inertial particles in wall-bounded turbulent flows is investigated through large-scale direct numerical simulations (DNS) of particle-laden canonical channel flow spanning almost a decade in the friction Reynolds number, from $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Re}_{\tau } = 150$ to 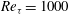$\mathit{Re}_{\tau } = 1000$. Lagrangian particle tracking is used to study the motion of six different particle sets, described by a Stokes number in the range 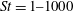$\mathit{St} = 1\text {--}1000$. At all Reynolds numbers a strong segregation in the near-wall region is observed for particles characterized by intermediate Stokes number, in the range 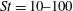$\mathit{St} =10\text {--}100$. The wall-normal concentration profiles of such particles collapse in inner scaling, thus suggesting the independence of the turbophoretic drift from the large-scale outer motions. This observation is also supported by the spatial organization of the suspended phase in the inner layer, which is found to be universal with the Reynolds number. The deposition rate coefficient increases with 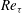$\mathit{Re}_{\tau }$ for a given 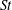$\mathit{St}$. Suitable inner and outer scalings are proposed to collapse the deposition curves across the available ranges of Reynolds and Stokes numbers for the different deposition regimes.

JFM classification

Turbulent Flows: Turbulent boundary layers
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 758 , 10 November 2014 , R1
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arcen, B., Taniér, A. & Oesterlè, B. 2006 On the influence of near wall forces in particle-laden channel flows. Intl J. Multiphase Flow 32, 1326–1339.CrossRefGoogle Scholar
Armenio, V. & Fiorotto, V. 2001 The importance of the forces acting on particles in turbulent flows. Phys. Fluids 13, 2437–2440.Google Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2013a The effect of large-scale turbulent structures on particle dispersion in wall-bounded flows. Intl J. Multiphase Flow 51, 55–64.Google Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to ${\mathit{Re}}_{\tau }=4000$ . J. Fluid Mech. 742, 171–191.Google Scholar
Bernardini, M., Pirozzoli, S., Quadrio, M. & Orlandi, P. 2013b Turbulent channel flow simulations in convecting reference frames. J. Comput. Phys. 232, 1–6.Google Scholar
Brooke, J. W., Kontomaris, K., Hanratty, T. J. & McLaughlin, J. B. 1992 Turbulent deposition and trapping of aerosols at a wall. Phys. Fluids 4, 825–834.Google Scholar
Caporaloni, M., Tampieri, F., Trombetti, F. & Vittori, O. 1975 Transfer of particles in nonisotropic air turbulence. J. Atmos. Sci. 32, 565–568.Google Scholar
Eaton, J. K. & Fessler, J. R. 1994 Preferential concentration of particles by turbulence. Intl J. Multiphase Flow 20, 169–209.Google Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22, 071704.Google Scholar
Friedlander, S. K. & Johnstone, H. F. 1957 Deposition of suspended particles from turbulent gas streams. Ind. Engng Chem. 49, 1151–1156.CrossRefGoogle Scholar
García, M., Lopez, F. & Niño, Y. 1995 Characterization of near-bed coherent structures in turbulent open-channel flow using synchronized high-speed video and hot-film measurements. Exp. Fluids 19, 16–28.Google Scholar
Guha, A. 2008 Transport and deposition of particles in turbulent and laminar flow. Annu. Rev. Fluid Mech. 40, 311–341.Google Scholar
van Haarlem, B., Boersma, J. B. & Nieuwstadt, F. T. M. 1998 Direct numerical simulation of particle deposition onto a free-slip and no-slip surface. Phys. Fluids 10, 2608–2620.Google Scholar
Kaftori, D., Hetsroni, G. & Banerjee, S. 1995 Particle behavior in the turbulent boundary layer. Part I: motion, deposition and entrainment. Phys. Fluids 7, 1095–1106.Google Scholar
Liu, B. Y. H. & Agarwal, J. K. 1974 Experimental observation of aerosol deposition in turbulent flow. Aerosol Sci. 568, 145–155.Google Scholar
Marchioli, C., Giusti, A., Salvetti, M. V. & Soldati, A. 2003 Direct numerical simulation of particle wall transfer and deposition in upward turbulent pipe flow. Intl J. Multiphase Flow 29, 1017–1038.Google Scholar
Marchioli, C., Picciotto, M. & Soldati, A. 2007 Influence of gravity and lift on particle velocity statistics and transfer rates in turbulent vertical channel flow. Intl J. Multiphase Flow 33, 227–251.Google Scholar
Marchioli, C. & Soldati, A. 2002 Mechanisms for particle transfer and segregation in a turbulent boundary layer. J. Fluid Mech. 468, 283–315.Google Scholar
Marchioli, C. & Soldati, A. 2007 Reynolds number scaling of particle preferential concentration in turbulent channel flow. In Advances in Turbulence XI, pp. 298–300. Springer.CrossRefGoogle Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22, 065103.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26, 883–889.Google Scholar
McCoy, D. D. & Hanratty, T. J. 1977 Rate of deposition of droplets in annular two phase flow. Intl J. Multiphase Flow 3, 319–331.Google Scholar
Milici, B., De Marchis, M., Sardina, G. & Napoli, E. 2014 Effects of roughness on particle dynamics in turbulent channel flows: a DNS analysis. J. Fluid Mech. 739, 465–478.Google Scholar
Narayanan, C., Lakehal, D., Botto, L. & Soldati, A. 2003 Mechanisms of particle deposition in a fully developed turbulent open channel flow. Phys. Fluids 15, 763–775.Google Scholar
Nilsen, C., Andersson, H. I. & Zhao, L. 2013 A Voronoï analysis of preferential concentration in a vertical channel flow. Phys. Fluids 25, 115108.CrossRefGoogle Scholar
Nowbahar, A., Sardina, G., Picano, F. & Brandt, L. 2013 Turbophoresis attenuation in a turbulent channel flow with polymer additives. J. Fluid Mech. 732, 706–719.CrossRefGoogle Scholar
Pan, Y. & Banerjee, S. 1996 Numerical simulation of particle interaction with wall turbulence. Phys. Fluids 8, 2733–2755.Google Scholar
Picano, F., Sardina, G. & Casciola, C. M. 2009 Spatial development of particle-laden turbulent pipe flow. Phys. Fluids 21, 093305.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Reeks, M. W. 1983 The transport of discrete particles in turbulent flows. J. Aerosol Sci. 14, 729–739.Google Scholar
Righetti, M. & Romano, G. P. 2004 Particle–fluid interactions in a plane nearwall turbulent flow. J. Fluid Mech. 505, 93–121.Google Scholar
Rouson, D. W. I. & Eaton, J. K. 2001 On the preferential concentration of solid particles in turbulent channel flow. J. Fluid Mech. 428, 149–169.Google Scholar
Sardina, G., Picano, F., Schlatter, P., Brandt, L. & Casciola, C. M. 2011 Large scale accumulation patterns of inertial particles in wall-bounded turbulent flow. Flow Turbul. Combust. 86, 519–532.Google Scholar
Sardina, G., Picano, F., Schlatter, P., Brandt, L. & Casciola, C. M. 2014 Statistics of particle accumulation in spatially developing turbulent boundary layers. Flow Turbul. Combust. 92, 27–40.Google Scholar
Sardina, G., Schlatter, P., Picano, F., Casciola, C. M., Brandt, L. & Henningson, D. S. 2012 Self-similar transport of inertial particles in a turbulent boundary layer. J. Fluid Mech. 706, 584–596.Google Scholar
Soldati, A. & Marchioli, C. 2009 Physics and modelling of turbulent particle deposition and entrainment: review of a systematic study. Intl J. Multiphase Flow 35, 827–839.Google Scholar
Uijttewaal, W. S. J. & Oliemans, R. V. A. 1996 Particle dispersion and deposition in direct numerical and large eddy simulations of vertical pipe flows. Phys. Fluids 8, 2590–2604.Google Scholar
Vinkovic, I., Doppler, D., Lelouvetel, J. & Buffat, M. 2011 Physics and modelling of turbulent particle deposition and entrainment: review of a systematic study. Intl J. Multiphase Flow 37, 187–197.Google Scholar
Young, J. & Leeming, A. 1997 A theory of particle deposition in turbulent pipe flow. J. Fluid Mech. 340, 129–159.CrossRefGoogle Scholar