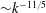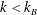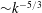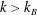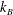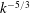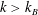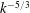1 Introduction
Stable density stratification is commonly observed in oceans and the nocturnal atmosphere (Sagaut & Cambon Reference Sagaut and Cambon2008; Turner Reference Turner2009; Davidson Reference Davidson2013; Maffioli & Davidson Reference Maffioli and Davidson2016). Both atmospheric and oceanic flow can often be turbulent; such turbulence, commonly known as ‘stably stratified turbulence’ (SST), is different from the classical ‘Kolmogorov turbulence’, which is applicable to homogeneous and isotropic hydrodynamic turbulence.
Stably stratified turbulence is quite complex, and there are many unresolved issues in this field (Lindborg Reference Lindborg2006, Reference Lindborg2007; Brethouwer et al. Reference Brethouwer, Billant, Lindborg and Chomaz2007; Davidson Reference Davidson2013; Rosenberg et al. Reference Rosenberg, Pouquet, Marino and Mininni2015; Verma Reference Verma2018). One of the important parameters here is the Froude number
$$\begin{eqnarray}\displaystyle Fr\equiv \frac{U}{NL}, & & \displaystyle\end{eqnarray}$$
where
$U$
and
$L$
are the large-scale velocity and length scale, respectively, and
$N$
is the Brunt–Väisälä frequency (defined in § 2) (Davidson Reference Davidson2013). A related parameter is the Richardson number,
$$\begin{eqnarray}\displaystyle Ri\equiv \frac{N^{2}}{(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}z)^{2}}, & & \displaystyle\end{eqnarray}$$
which is the ratio of buoyancy and flow shear. The approximation
$\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}z\sim U/L$
yields
$Ri\approx Fr^{-2}$
(Rosenberg et al.
Reference Rosenberg, Pouquet, Marino and Mininni2015; Maffioli, Brethouwer & Lindborg Reference Maffioli, Brethouwer and Lindborg2016). The degree of turbulence is quantified by the Reynolds number,
$Re\equiv UL/\unicode[STIX]{x1D708}$
, where
$\unicode[STIX]{x1D708}$
is the kinematic viscosity of the fluid.
Based on the above parameters, stably stratified turbulent flows can be classified into three broad regimes:
(1)
$Re\gg 1$
and
$Fr\gg 1$
(turbulent SST with weak buoyancy): In this regime, strong nonlinearity (
$\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}$
) in comparison to buoyancy yields scaling similar to passive scalar turbulence. Hence, both the kinetic energy spectrum,
$E_{u}(k)$
, and potential energy spectrum,
$E_{b}(k)$
, follow the Kolmogorov spectrum and scale as
${\sim}k^{-5/3}$
, where
$k$
denotes wavenumber.(2)
$Re\gg 1$
and
$Fr\ll 1$
(turbulent SST with strong buoyancy): Here, buoyancy is much stronger than the nonlinearity. The flow is strongly anisotropic, with strong horizontal velocity compared to the vertical velocity (Vallis, Shutts & Gray Reference Vallis, Shutts and Gray1997; Lindborg Reference Lindborg2006, Reference Lindborg2007; Brethouwer et al.
Reference Brethouwer, Billant, Lindborg and Chomaz2007; Davidson Reference Davidson2013). The flow of the terrestrial atmosphere is strongly stratified with typical
$Fr\sim 0.01$
(Waite Reference Waite2011). The physics of this regime is quite complex, and it is still being debated.(3)
$Re\gg 1$
and
$Fr\approx 1$
(turbulent SST with moderate buoyancy): Here, buoyancy and nonlinearity are of comparable strength. Bolgiano (Reference Bolgiano1959) and Obukhov (Reference Obukhov1959) constructed a model for this regime by arguing that the buoyancy force converts kinetic energy into potential energy. They argued for a dual scaling, with transition occurring at Bolgiano wavenumber
$k_{B}$
. For
$k<k_{B}$
, the kinetic energy flux
$\unicode[STIX]{x1D6F1}_{u}(k)$
decreases as
${\sim}k^{-4/5}$
, but the potential energy flux
$\unicode[STIX]{x1D6F1}_{b}(k)$
is constant. Here,
$E_{u}(k)\sim k^{-11/5}$
and
$E_{b}(k)\sim k^{-7/5}$
. For
$k>k_{B}$
, buoyancy is expected to be weak, and hence the scaling is similar to that for a passive scalar. We denote the above model as the Bolgiano–Obukhov (BO) phenomenology.
In this paper we focus on the third regime – moderately stratified turbulence. For this, computational studies by Waite & Bartello (Reference Waite and Bartello2004) and Kumar, Chatterjee & Verma (Reference Kumar, Chatterjee and Verma2014) show that the flow remains approximately isotropic. Furthermore, the direct numerical simulation results of Kimura & Herring (Reference Kimura and Herring1996) and Kumar et al. (Reference Kumar, Chatterjee and Verma2014), the shell-model results of Kumar & Verma (Reference Kumar and Verma2015) and the global energy balance analysis of Bhattacharjee (Reference Bhattacharjee2015) have unequivocally shown that the kinetic energy spectrum indeed scales as
${\sim}k^{-11/5}$
in a wavenumber band. However, we are not aware of any numerical or experimental work that convincingly demonstrates the dual scaling for such flows.
Several researchers have reported BO scaling for turbulent thermal convection, Rayleigh–Taylor turbulence and unstably stratified flows. Note, however, that Verma, Kumar & Pandey (Reference Verma, Kumar and Pandey2017) showed that BO scaling is not applicable to such flows in three dimensions; instead, they follow Kolmogorov-like turbulence phenomenology (
$E_{u}(k)\sim k^{-5/3}$
). Yet, in two dimensions, turbulent thermal convection and Rayleigh–Taylor turbulence exhibit BO scaling, as demonstrated by Boffetta et al. (Reference Boffetta, De Lillo, Mazzino and Musacchio2012) and Boffetta & Mazzino (Reference Boffetta and Mazzino2017). Verma et al. (Reference Verma, Kumar and Pandey2017) and Verma (Reference Verma2018) argued that the above phenomenon is due to the inverse cascade of kinetic energy.
The flow in the deep oceans is moderately stratified with
$Fr\sim 1$
(Petrolo & Woods Reference Petrolo and Woods2019). The atmosphere of some other planets could yield a wide range of
$Fr$
; hence, a clear understanding of SST with moderate buoyancy is essential. The goal of this paper is to revisit turbulent SST with moderate buoyancy and critically examine the validity of dual scaling of the BO phenomenology. We start with the constancy of the total energy flux (kinetic plus potential) and demonstrate that, for large wavenumbers, the velocity field becomes weak; hence, the assumption that buoyancy becomes weak at large wavenumbers leading to
$k^{-5/3}$
spectra is improbable. We observe that
$E_{u}(k)\sim k^{-11/5}$
for
$k>1/L$
, where
$L$
is the system size, with no cross-over to
$k^{-5/3}$
spectra. As an aside, we recover
$E_{u}(k)=k^{-5/3}$
for
$k<1/L$
, which may be possible in systems with large aspect ratio. Thus, we provide a revision of the celebrated BO phenomenology.
The outline of the paper is as follows. The equations governing SST are introduced in § 2. The BO phenomenology is described in § 3. In § 4.1 and § 4.2, respectively, numerical solution and asymptotic analysis of the equation for the total energy flux (a fifth-order equation) are presented. We conclude in § 5.
2 Governing equations
The governing Navier–Stokes equations for stably stratified flows (density stratification in the vertical (
$z$
) direction) under the Boussinesq approximation are (Davidson Reference Davidson2004, Reference Davidson2013; Lindborg Reference Lindborg2006; Verma Reference Verma2018)
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}t}+(\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\boldsymbol{u}=-\frac{1}{\unicode[STIX]{x1D70C}_{m}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D70E}-Nb\hat{z}+\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}+\boldsymbol{F}_{u}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}b}{\unicode[STIX]{x2202}t}+(\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735})b=Nu_{z}+\unicode[STIX]{x1D705}\unicode[STIX]{x1D6FB}^{2}b, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0. & \displaystyle\end{eqnarray}$$
$\boldsymbol{u}=(u_{x},u_{y},u_{z})$
and
$\unicode[STIX]{x1D70E}$
are, respectively, the velocity and the pressure fields;
$\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D705}$
are respectively the kinematic viscosity and diffusivity of the density fluctuation;
$\unicode[STIX]{x1D70C}_{m}$
is the mean density;
$\boldsymbol{F}_{u}$
is the external force (in addition to the buoyancy); and
$b$
is the density fluctuation in velocity units, which is achieved by the following transformation (Lindborg Reference Lindborg2006; Davidson Reference Davidson2013; Rosenberg et al.
Reference Rosenberg, Pouquet, Marino and Mininni2015): 
$$\begin{eqnarray}\displaystyle b=\frac{g}{N}\frac{\unicode[STIX]{x1D70C}}{\unicode[STIX]{x1D70C}_{m}}, & & \displaystyle\end{eqnarray}$$
where
$g$
is the acceleration due to gravity and
$\unicode[STIX]{x1D70C}$
is the density fluctuation. The quantity
$$\begin{eqnarray}\displaystyle N=\sqrt{\frac{g}{\unicode[STIX]{x1D70C}_{m}}\left|\frac{\text{d}\bar{\unicode[STIX]{x1D70C}}}{\text{d}z}\right|} & & \displaystyle\end{eqnarray}$$
is the Brunt–Väisälä frequency. Note that
$-Nb$
is buoyancy.
It is convenient to describe the flow behaviour in Fourier space since it captures the scale-by-scale energy transfer and interactions. The following one-dimensional kinetic spectrum,
$E_{u}(k)$
, and the potential energy spectrum,
$E_{b}(k)$
, which are the sums of the respective energy of all the modes of a shell of thickness
$\text{d}k$
, are introduced:
$$\begin{eqnarray}\displaystyle & \displaystyle E_{u}(k,t)\,\text{d}k=\mathop{\sum }_{k<|\boldsymbol{k}^{\prime }|\leqslant k+\text{d}k}\frac{1}{2}|\boldsymbol{u}(\boldsymbol{k}^{\prime },t)|^{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle E_{b}(k,t)\,\text{d}k=\mathop{\sum }_{k<|\boldsymbol{k}^{\prime }|\leqslant k+\text{d}k}\frac{1}{2}|b(\boldsymbol{k}^{\prime },t)|^{2}. & \displaystyle\end{eqnarray}$$
Note that
$E_{u}(k)$
and
$E_{b}(k)$
are averaged over polar angles; hence they do not capture the anisotropic effects. The ring spectrum proposed by Teaca et al. (Reference Teaca, Verma, Knaepen and Carati2009) and Nath et al. (Reference Nath, Pandey, Kumar and Verma2016) captures the angular-dependent spectra.
Henceforth, the explicit time dependence in
$E_{u}$
and
$E_{b}$
is suppressed for brevity. The nonlinear energy transfers across modes are quantified using energy fluxes or energy cascade rates. The kinetic (potential) energy flux,
$\unicode[STIX]{x1D6F1}_{u(b)}(k_{0})$
, for a wavenumber sphere of radius
$k_{0}$
is the total kinetic (potential) energy leaving the said sphere due to nonlinear interactions. These fluxes are computed using the following formulae (Dar, Verma & Eswaran Reference Dar, Verma and Eswaran2001; Verma Reference Verma2004, Reference Verma2018):
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{u}(k_{0})=\mathop{\sum }_{|\boldsymbol{k}|>k_{0}}\mathop{\sum }_{|\boldsymbol{p}|\leqslant k_{0}}\text{Im}[\{\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{u}(\boldsymbol{q})\}\{\boldsymbol{u}(\boldsymbol{p})\boldsymbol{\cdot }\boldsymbol{u}^{\ast }(\boldsymbol{k})\}], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{b}(k_{0})=\mathop{\sum }_{|\boldsymbol{k}|>k_{0}}\mathop{\sum }_{|\boldsymbol{p}|\leqslant k_{0}}\text{Im}[\{\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{u}(\boldsymbol{q})\}\{b(\boldsymbol{p})b^{\ast }(\boldsymbol{k})\}], & \displaystyle\end{eqnarray}$$
$\boldsymbol{k}=\boldsymbol{p}+\boldsymbol{q}$
. The dynamical equations for modal kinetic energy (
$E_{u}(\boldsymbol{k})=(1/2)|\boldsymbol{u}(\boldsymbol{k})|^{2}$
) and potential energy (
$E_{b}(\boldsymbol{k})=(1/2)|b(\boldsymbol{k})|^{2}$
), respectively, can be derived from (2.1a
) and (2.1b
), and are as follows (Davidson Reference Davidson2013; Verma Reference Verma2018):
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}E_{u}(\boldsymbol{k})=T_{u}(\boldsymbol{k})+{\mathcal{F}}_{B}(\boldsymbol{k})+{\mathcal{F}}_{ext}(\boldsymbol{k})-D_{u}(\boldsymbol{k}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}E_{b}(\boldsymbol{k})=T_{b}(\boldsymbol{k})-{\mathcal{F}}_{B}(\boldsymbol{k})-D_{b}(\boldsymbol{k}). & \displaystyle\end{eqnarray}$$
$T_{u(b)}(\boldsymbol{k})$
and
$D_{u(b)}(\boldsymbol{k})$
are, respectively, the nonlinear kinetic (potential) energy transfer rate and dissipation rate, while
${\mathcal{F}}_{B}$
and
${\mathcal{F}}_{ext}$
denote the energy feed rate by the buoyancy and external force, respectively. These quantities are defined as follows (Verma et al.
Reference Verma, Kumar and Pandey2017; Verma Reference Verma2018): 
$$\begin{eqnarray}\displaystyle & \displaystyle T_{u}(\boldsymbol{k})=\mathop{\sum }_{\boldsymbol{p}}\text{Im}[\{\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{u}(\boldsymbol{q})\}\{\boldsymbol{u}(\boldsymbol{p})\boldsymbol{\cdot }\boldsymbol{u}^{\ast }(\boldsymbol{k})\}], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle T_{b}(\boldsymbol{k})=\mathop{\sum }_{\boldsymbol{p}}\text{Im}[\{\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{u}(\boldsymbol{q})\}\{b(\boldsymbol{p})b^{\ast }(\boldsymbol{k})\}], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}_{B}(\boldsymbol{k})=-N\text{Re}[b(\boldsymbol{k})u_{z}^{\ast }(\boldsymbol{k})], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}_{ext}(\boldsymbol{k})=\text{Re}[\boldsymbol{F}_{u}(\boldsymbol{k})\boldsymbol{\cdot }\boldsymbol{u}^{\ast }(\boldsymbol{k})], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle D_{u}(\boldsymbol{k})=2\unicode[STIX]{x1D708}k^{2}E_{u}(\boldsymbol{k}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle D_{b}(\boldsymbol{k})=2\unicode[STIX]{x1D705}k^{2}E_{b}(\boldsymbol{k}), & \displaystyle\end{eqnarray}$$
$\boldsymbol{k}=\boldsymbol{p}+\boldsymbol{q}$
. The kinetic and potential energy fluxes are related to nonlinear energy transfer terms as 
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}_{u}(\boldsymbol{k}_{\mathbf{0}})=-\mathop{\sum }_{|\boldsymbol{k}|\leqslant k_{0}}T_{u}(\boldsymbol{k}),\quad \unicode[STIX]{x1D6F1}_{b}(\boldsymbol{k}_{\mathbf{0}})=-\mathop{\sum }_{|\boldsymbol{k}|\leqslant k_{0}}T_{b}(\boldsymbol{k}). & & \displaystyle\end{eqnarray}$$
We write (2.7a
) and (2.7b
) for the spheres of radii
$k$
and
$k+\text{d}k$
and take their difference, which yields
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\mathop{\sum }_{k<|\boldsymbol{k}^{\prime }|\leqslant k+\text{d}k}E_{u}(\boldsymbol{k}^{\prime })=\mathop{\sum }_{k<|\boldsymbol{k}^{\prime }|\leqslant k+\text{d}k}T_{u}(\boldsymbol{k}^{\prime })+{\mathcal{F}}_{B}(\boldsymbol{k}^{\prime })+{\mathcal{F}}_{ext}(\boldsymbol{k}^{\prime })-D_{u}(\boldsymbol{k}^{\prime }), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\mathop{\sum }_{k<|\boldsymbol{k}^{\prime }|\leqslant k+\text{d}k}E_{b}(\boldsymbol{k}^{\prime })=\mathop{\sum }_{k<|\boldsymbol{k}^{\prime }|\leqslant k+\text{d}k}T_{b}(\boldsymbol{k}^{\prime })-{\mathcal{F}}_{B}(\boldsymbol{k}^{\prime })-D_{b}(\boldsymbol{k}^{\prime }), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathop{\sum }_{k<|\boldsymbol{k}^{\prime }|\leqslant k+\text{d}k}T_{u}(\boldsymbol{k}^{\prime })=-\unicode[STIX]{x1D6F1}_{u}(k+\text{d}k)+\unicode[STIX]{x1D6F1}_{u}(k), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathop{\sum }_{k<|\boldsymbol{k}^{\prime }|\leqslant k+\text{d}k}T_{b}(\boldsymbol{k}^{\prime })=-\unicode[STIX]{x1D6F1}_{b}(k+\text{d}k)+\unicode[STIX]{x1D6F1}_{b}(k). & \displaystyle\end{eqnarray}$$
$\text{d}k\rightarrow 0$
yields 
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}E_{u}(k)=-\frac{\text{d}}{\text{d}k}\unicode[STIX]{x1D6F1}_{u}(k)+{\mathcal{F}}_{B}(k)+{\mathcal{F}}_{ext}(k)-D_{u}(k), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}E_{b}(k)=-\frac{\text{d}}{\text{d}k}\unicode[STIX]{x1D6F1}_{b}(k)-{\mathcal{F}}_{B}(k)-D_{b}(k), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}_{B}(k)\,\text{d}k=-\mathop{\sum }_{k<|\boldsymbol{k}^{\prime }|\leqslant k+\text{d}k}N\text{Re}[b(\boldsymbol{k}^{\prime })u_{z}^{\ast }(\boldsymbol{k}^{\prime })], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}_{ext}(k)\,\text{d}k=\mathop{\sum }_{k<|\boldsymbol{k}^{\prime }|\leqslant k+\text{d}k}\text{Re}[\boldsymbol{F}_{u}(\boldsymbol{k}^{\prime })\boldsymbol{\cdot }\boldsymbol{u}^{\ast }(\boldsymbol{k}^{\prime })], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle D_{u}(k)\,\text{d}k=2\unicode[STIX]{x1D708}\mathop{\sum }_{k<|\boldsymbol{k}^{\prime }|\leqslant k+\text{d}k}{k^{\prime }}^{2}E_{u}(\boldsymbol{k}^{\prime }), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle D_{b}(k)\,\text{d}k=2\unicode[STIX]{x1D705}\mathop{\sum }_{k<|\boldsymbol{k}^{\prime }|\leqslant k+\text{d}k}{k^{\prime }}^{2}E_{b}(\boldsymbol{k}^{\prime }). & \displaystyle\end{eqnarray}$$
Figure 1. (a) The kinetic energy content of a wavenumber shell changes due to the kinetic energy flux difference
$\unicode[STIX]{x1D6F1}_{u}(k+\text{d}k)-\unicode[STIX]{x1D6F1}_{u}(k)$
, energy removal rate by buoyancy
${\mathcal{F}}_{B}(k)\,\text{d}k$
, and viscous dissipation rate
$D_{u}(k)\,\text{d}k$
. (b) The potential energy changes due to potential energy flux difference
$\unicode[STIX]{x1D6F1}_{b}(k+\text{d}k)-\unicode[STIX]{x1D6F1}_{b}(k)$
, energy supply rate by buoyancy
${\mathcal{F}}_{B}(k)\,\text{d}k$
, and dissipation rate
$D_{b}(k)\,\text{d}k$
.
Let us consider a statistically steady state (
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t\rightarrow 0$
). In the inertial range,
${\mathcal{F}}_{ext}=0$
, and the dissipative effects are negligible, i.e.
$D_{u}\rightarrow 0$
and
$D_{b}\rightarrow 0$
. Hence the equations for the kinetic and potential energies simplify to
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}k}\unicode[STIX]{x1D6F1}_{u}(k)={\mathcal{F}}_{B}(k), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}k}\unicode[STIX]{x1D6F1}_{b}(k)=-{\mathcal{F}}_{B}(k). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}_{u}(k)+\unicode[STIX]{x1D6F1}_{b}(k)=\unicode[STIX]{x1D6F1}=\text{const}. & & \displaystyle\end{eqnarray}$$
Hence the total energy flux is constant in the inertial range. We will employ (2.15) in the later part of the paper.
Based on energetics arguments, it has been shown that the energy injection rate by buoyancy,
${\mathcal{F}}_{B}$
, is negative. Hence
$\unicode[STIX]{x1D6F1}_{u}(k)$
decreases with
$k$
(Kumar et al.
Reference Kumar, Chatterjee and Verma2014; Verma Reference Verma2018, Reference Verma2019). Verma (Reference Verma2019) showed that, in the linear regime, gravity waves facilitate periodic exchange of kinetic and potential energies, hence
${\mathcal{F}}_{B}=0$
. Therefore, a non-dissipative gravity wave represents a neutral state. Since the system is stable, the nonlinearity makes
${\mathcal{F}}_{B}$
negative. If
${\mathcal{F}}_{B}>0$
, according to the integral form of (2.7a
), the kinetic energy would grow in time, thus making the flow unstable. Hence,
${\mathcal{F}}_{B}<0$
. In addition, Kumar et al. (Reference Kumar, Chatterjee and Verma2014) and Verma (Reference Verma2019) go on to argue that
${\mathcal{F}}_{B}(k)<0$
. The above features have been verified numerically by Kumar et al. (Reference Kumar, Chatterjee and Verma2014) and Verma et al. (Reference Verma, Kumar and Pandey2017).
When we substitute negative
${\mathcal{F}}_{B}(k)$
in (2.14a
) and (2.14b
), we deduce that
$\unicode[STIX]{x1D6F1}_{u}(k)$
decreases with
$k$
, while
$\unicode[STIX]{x1D6F1}_{b}(k)$
increases with
$k$
. These features play an important role in the models of Bolgiano (Reference Bolgiano1959) and Obukhov (Reference Obukhov1959).
The equations described in this section apply to all three regimes. In the following two sections we will focus on phenomenology of moderately stratified turbulence.
3 The Bolgiano–Obukhov phenomenology for moderately stably stratified turbulence
Bolgiano (Reference Bolgiano1959) and Obukhov (Reference Obukhov1959) constructed a phenomenology for moderately stratified turbulence, which we refer to as BO phenomenology. In this regime, the flow is nearly isotropic. Kumar et al. (Reference Kumar, Chatterjee and Verma2014) showed that for
$Fr\gtrsim 1$
the anisotropic ratio
$E_{\bot }/2E_{\Vert }\approx 1$
, where
$E_{\bot }=(u_{x}^{2}+u_{y}^{2})/2$
and
$E_{\Vert }=u_{z}^{2}/2$
. Waite & Bartello (Reference Waite and Bartello2004) also showed that the flow is approximately isotropic for
$Fr=1.3$
, and anisotropy of stratification starts to become visible for
$Fr\leqslant 0.21$
. It has been conjectured that isotropy is also present in the inertial range of moderately SST.
According to the BO phenomenology, a force balance between the nonlinear term and buoyancy in (2.1a ) yields
$$\begin{eqnarray}\displaystyle ku_{k}^{2}=Nb_{k}, & & \displaystyle\end{eqnarray}$$
where
$u_{k}$
and
$b_{k}$
are, respectively, the velocity and density fluctuations at wavenumber
$k$
. In addition, the BO phenomenology assumes that, in the inertial range,
$\unicode[STIX]{x1D6F1}_{b}(k)\approx \text{const.}$
, and it equals the dissipation rate of the potential energy (
$\unicode[STIX]{x1D716}_{b}$
):
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}_{b}(k)=kb_{k}^{2}u_{k}=\unicode[STIX]{x1D716}_{b}. & & \displaystyle\end{eqnarray}$$
Equations (3.1) and (3.2) yield the following relations:
$$\begin{eqnarray}\displaystyle & \displaystyle E_{u}(k)=\frac{u_{k}^{2}}{k}=c_{1}\unicode[STIX]{x1D716}_{b}^{2/5}N^{4/5}k^{-11/5}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle E_{b}(k)=\frac{b_{k}^{2}}{k}=c_{2}\unicode[STIX]{x1D716}_{b}^{4/5}N^{-2/5}k^{-7/5}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{u}(k)=ku_{k}^{3}=c_{3}\unicode[STIX]{x1D716}_{b}^{3/5}N^{6/5}k^{-4/5}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{b}(k)=\unicode[STIX]{x1D716}_{b}. & \displaystyle\end{eqnarray}$$
Bolgiano (Reference Bolgiano1959) and Obukhov (Reference Obukhov1959) argued that the above-mentioned behaviour of the inertial range is true only for lower wavenumbers (
$k<k_{B}$
, where
$k_{B}$
will be defined below). For
$k>k_{B}$
of the inertial range, the buoyancy effects are weak and hence cannot balance the inertial term (which is balanced by the pressure gradient). Hence in this region, the scaling of passive scalar (i.e. Kolmogorov) turbulence should be valid. The energy and flux relations obtained here are
$$\begin{eqnarray}\displaystyle & \displaystyle E_{u}(k)=K_{Ko}\unicode[STIX]{x1D716}_{u}^{2/3}k^{-5/3}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle E_{b}(k)=K_{OC}\unicode[STIX]{x1D716}_{u}^{-1/3}\unicode[STIX]{x1D716}_{b}k^{-5/3}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{u}(k)=\unicode[STIX]{x1D716}_{u}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{b}(k)=\unicode[STIX]{x1D716}_{b}, & \displaystyle\end{eqnarray}$$
$\unicode[STIX]{x1D716}_{u}$
is the viscous dissipation rate, and
$K_{Ko}$
and
$K_{OC}$
are the Kolmogorov and Obukhov–Corrsin constants. It is important to keep in mind that the viscous dissipation and thermal dissipation play a critical role in turbulence. They set up the fluxes,
$\unicode[STIX]{x1D6F1}_{u}$
and
$\unicode[STIX]{x1D6F1}_{b}$
, even though they are not very active in the inertial range. The behavioural transition from one regime to another occurs near the Bolgiano wavenumber
$k_{B}$
, which is obtained by matching
$\unicode[STIX]{x1D6F1}_{u}(k)$
in the two regimes:
$$\begin{eqnarray}\displaystyle k_{B}\approx N^{3/2}\unicode[STIX]{x1D716}_{u}^{-5/4}\unicode[STIX]{x1D716}_{b}^{3/4}. & & \displaystyle\end{eqnarray}$$
The nature of kinetic and potential energy fluxes, as well as dual scaling of moderately SST as predicted by Bolgiano (Reference Bolgiano1959) and Obukhov (Reference Obukhov1959), are illustrated in figure 2. We also remark that
$\unicode[STIX]{x1D6F1}_{u}(k)$
decreases rapidly as
$k^{-4/5}$
and then it tapers off to
$\unicode[STIX]{x1D716}_{u}$
. However,
$\unicode[STIX]{x1D6F1}_{b}\approx \unicode[STIX]{x1D716}_{b}\approx \unicode[STIX]{x1D6F1}$
(see (2.15)). Hence,
$\unicode[STIX]{x1D716}_{b}\gg \unicode[STIX]{x1D716}_{u}$
.
Figure 2. Schematic diagram of moderately SST according to the BO phenomenology. (a) Kinetic energy flux and (b) potential energy flux. The transition from the inertial regime to the dissipation regime occurs at wavenumber
$k_{DI}$
. Here
$k_{d}$
is the Kolmogorov wavenumber, and
$k_{d}\gg k_{DI}$
.
In addition to
$k_{B}$
, another important length referred to in SST is the ‘Ozmidov length’, which is defined as
$$\begin{eqnarray}\displaystyle L_{O}\equiv \sqrt{\frac{\unicode[STIX]{x1D716}_{u}}{N^{3}}}. & & \displaystyle\end{eqnarray}$$
The corresponding wavenumber
$k_{O}=1/L_{O}$
. At
$L_{O}$
, the time scales of gravity waves and local eddies match, i.e.
$l/u_{l}\approx 1/N$
. Using a numerical simulation, Waite & Bartello (Reference Waite and Bartello2004, Reference Waite and Bartello2006) computed
$L_{O}$
for
$Fr=1.3$
and reported that
$L_{O}$
is approximately
$1/31$
of the system size.
For moderately stratified flows,
$\unicode[STIX]{x1D6F1}_{u}(k)$
varies with
$k$
; hence it is not obvious whether we should substitute
$\unicode[STIX]{x1D716}_{u}=\unicode[STIX]{x1D6F1}_{u}(k)$
of (3.3c
), or
$\unicode[STIX]{x1D716}_{u}$
of (3.4c
). In any case, it is interesting to compare
$k_{O}$
with
$k_{B}$
. Using (3.5) and (3.6) we obtain
$$\begin{eqnarray}\displaystyle \frac{k_{B}}{k_{O}}=\unicode[STIX]{x1D716}_{u}^{-5/4+1/2}\unicode[STIX]{x1D716}_{b}^{3/4}\sim \left(\frac{\unicode[STIX]{x1D716}_{b}}{\unicode[STIX]{x1D716}_{u}}\right)^{3/4}. & & \displaystyle\end{eqnarray}$$
Since
$\unicode[STIX]{x1D716}_{b}\gg \unicode[STIX]{x1D716}_{u}$
for SST, we expect that
$k_{B}\gg k_{O}$
.
In the next section, we describe certain critical deficiencies of the BO phenomenology.
4 Revision of Bolgiano–Obukhov phenomenology for moderately stably stratified turbulence
A crucial assumption made in the BO phenomenology is that
$\unicode[STIX]{x1D6F1}_{b}(k)\approx \text{const.}$
in the inertial range (refer to (3.2)). This assumption needs a closer examination. A more rigorous approach would be to start with the constancy of total energy flux (2.15) that follows from the conservation of total energy (kinetic plus potential) in the inviscid limit.
We start with (2.15), and equate it to the total dissipation rate
$\unicode[STIX]{x1D716}$
. That is,
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}_{u}(k)+\unicode[STIX]{x1D6F1}_{b}(k)=ku_{k}^{3}+kb_{k}^{2}u_{k}=\unicode[STIX]{x1D716}. & & \displaystyle\end{eqnarray}$$
In the above equation we eliminate
$b_{k}$
using (3.1), which yields the following fifth-order polynomial in
$u_{k}$
:
$$\begin{eqnarray}\displaystyle ku_{k}^{3}+\frac{k^{3}u_{k}^{5}}{N^{2}}=\unicode[STIX]{x1D716}. & & \displaystyle\end{eqnarray}$$
There is no analytical solution for a fifth-order algebraic polynomial. Therefore, we employ numerical solution and asymptotic analysis to solve the above equation. These two results are consistent with each other.
4.1 Numerical solution
We numerically solve (4.2) using the ‘fsolve’ function of the SciPy library in Python, which uses Powell’s hybrid method to find zeros of nonlinear functions. We choose
$N=1.0$
, and the total energy flux
$\unicode[STIX]{x1D6F1}=1.0$
, which is also equal to the total dissipation rate
$\unicode[STIX]{x1D716}$
. We vary
$k$
from
$10^{-6}$
to
$10^{10}$
in logarithmic scale. These parameters can be treated as non-dimensional with the time period of a large-scale gravitational wave as the time scale, system size as the length scale, and large-scale velocity as the velocity scale. Using the numerically evaluated
$u_{k}$
and
$b_{k}$
, we evaluate
$E_{u}(k)=u_{k}^{2}/k$
,
$E_{b}(k)=b_{k}^{2}/k$
,
$\unicode[STIX]{x1D6F1}_{u}(k)=ku_{k}^{3}$
and
$\unicode[STIX]{x1D6F1}_{b}(k)=ku_{k}b_{k}^{2}$
. The quantities are plotted in figure 3.
Figure 3 exhibits the fluxes and spectra of the kinetic and potential energies. For
$1<k<10^{10}$
,
$\unicode[STIX]{x1D6F1}_{b}\approx 1$
,
$\unicode[STIX]{x1D6F1}_{u}(k)\sim k^{-4/5}$
,
$E_{u}\sim k^{-11/5}$
and
$E_{b}\sim k^{-7/5}$
, which are the predictions of the BO phenomenology for
$k<k_{B}$
. Surprisingly, there is no cross-over to
$k^{-5/3}$
scaling of passive scalar turbulence. This is because
$u_{k}\ll b_{k}$
; hence
$u_{k}$
cannot induce a constant kinetic energy flux. We will show a more rigorous derivation in the next subsection.
Interestingly, for
$k\ll 1$
, we obtain
$\unicode[STIX]{x1D6F1}_{u}\approx 1$
,
$\unicode[STIX]{x1D6F1}_{b}\sim k^{4/3}$
,
$E_{u}\sim k^{-5/3}$
and
$E_{b}\sim k^{-1/3}$
. That is,
$u_{k}$
dominates
$b_{k}$
at small
$k$
values, which leads to Kolmogorov’s scaling for the velocity field. Note, however, that
$k=1$
corresponds to
$1/L$
. Hence,
$k\ll 1$
is possible in SST when the transverse length scale is much larger than the vertical scale (
$L$
).
In the next two subsections we will perform asymptotic analysis of (4.1).
Figure 3. Fluxes and energy spectra for
$N=1.0$
and the total energy flux
$\unicode[STIX]{x1D6F1}=1.0$
. (a) Kinetic energy flux (
$\unicode[STIX]{x1D6F1}_{u}(k)$
) is plotted in red and potential energy flux (
$\unicode[STIX]{x1D6F1}_{b}(k)$
) is plotted in green. (b) Kinetic energy spectrum (
$E_{u}(k)$
) is plotted in red and potential energy spectrum (
$E_{b}(k)$
) is plotted in green. In both panels, black lines represent asymptotic behaviours in the extreme limits.
4.2 Asymptotic analysis
We examine the dominant balance for the two extreme limits of (4.2).
4.2.1 Case 1: moderately stably stratified turbulence for
$k\gg 1$
In this situation,
$\unicode[STIX]{x1D6F1}_{u}\ll \unicode[STIX]{x1D6F1}_{b}$
, and hence the balance is between
$\unicode[STIX]{x1D6F1}_{b}$
and
$\unicode[STIX]{x1D716}$
:
$$\begin{eqnarray}\displaystyle \frac{k^{3}u_{k}^{5}}{N^{2}}\approx \unicode[STIX]{x1D716}\quad \Longrightarrow \quad u_{k}\approx \unicode[STIX]{x1D716}^{1/5}N^{2/5}k^{-3/5}. & & \displaystyle\end{eqnarray}$$
Using (3.1),
$b_{k}$
is found to be
$$\begin{eqnarray}\displaystyle b_{k}\approx \unicode[STIX]{x1D716}^{2/5}N^{-1/5}k^{-1/5}. & & \displaystyle\end{eqnarray}$$
Therefore, the kinetic and potential energy spectra and fluxes, as well as the energy feed by buoyancy, are given by
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{u}(k)\approx \unicode[STIX]{x1D716}^{3/5}N^{6/5}k^{-4/5}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{b}(k)\approx \unicode[STIX]{x1D716}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}_{B}(k)=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}k}\unicode[STIX]{x1D6F1}_{u}(k)\approx -\frac{4}{5}\unicode[STIX]{x1D716}^{3/5}N^{6/5}k^{-9/5}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle E_{u}(k)\approx \unicode[STIX]{x1D716}^{2/5}N^{4/5}k^{-11/5}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle E_{b}(k)\approx \unicode[STIX]{x1D716}^{4/5}N^{-2/5}k^{-7/5}. & \displaystyle\end{eqnarray}$$
Note that
$u_{k}\sim k^{-3/5}$
decreases faster than
$b_{k}\sim k^{-1/5}$
. Therefore, buoyancy is strong enough so as to yield
$E_{u}(k)\sim k^{-11/5}$
for the whole of the inertial range, without a transition to the
$E_{u}(k)\sim k^{-5/3}$
regime. Note that the dissipation range starts after the inertial range.
A more quantitative condition for the absence of the second regime (
$k_{B}$
to
$k_{DI}$
of figure 2) is obtained as follows. Clearly, the Bolgiano wavenumber should be much smaller than the Kolmogorov wavenumber,
$k_{d}$
, which leads to
$$\begin{eqnarray}\displaystyle N^{6}\unicode[STIX]{x1D716}_{b}^{3}\unicode[STIX]{x1D716}_{u}^{-5}\ll \unicode[STIX]{x1D716}_{u}\unicode[STIX]{x1D708}^{-3}, & & \displaystyle\end{eqnarray}$$
or
$$\begin{eqnarray}\displaystyle N^{2}\unicode[STIX]{x1D708}\ll \unicode[STIX]{x1D716}_{u}^{2}\unicode[STIX]{x1D716}_{b}^{-1}. & & \displaystyle\end{eqnarray}$$
In the above equation, substitution of the following expressions for the Richardson number and thermal dissipation based on the root mean square quantities (Verma Reference Verma2018),
$$\begin{eqnarray}\displaystyle & \displaystyle Ri=\frac{Nb_{rms}L}{U^{2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D716}_{b}=\frac{Ub_{rms}^{2}}{L} & \displaystyle\end{eqnarray}$$
yields
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D716}_{u}\gg \frac{Ri}{\sqrt{Re}}\frac{U^{3}}{L}, & & \displaystyle\end{eqnarray}$$
where
$L$
is the length scale of the system. Using
$Ri\approx Fr^{-2}$
, we obtain
$$\begin{eqnarray}\displaystyle Re_{b}=ReFr^{2}\gg \frac{U^{3}/L}{\unicode[STIX]{x1D716}_{u}}, & & \displaystyle\end{eqnarray}$$
where
$Re_{b}$
is the buoyancy Reynolds number. As an example, for
$Fr=1.58$
, Maffioli et al. (Reference Maffioli, Brethouwer and Lindborg2016) obtained
$Re_{b}=10\,430$
. Interestingly, (4.11) is similar to that obtained by Brethouwer et al. (Reference Brethouwer, Billant, Lindborg and Chomaz2007) for strongly stratified turbulence.
Since
$\unicode[STIX]{x1D716}_{u}\ll \unicode[STIX]{x1D716}_{b}$
, the above condition may be very difficult to achieve in numerical simulations. If we assume that
$\unicode[STIX]{x1D716}_{u}=10^{-3}\unicode[STIX]{x1D716}_{b}\approx 10^{-3}U^{3}/L$
, for
$Fr=1$
, equation (4.11) predicts that
$Re\gg 10^{3}$
. Such a flow would be difficult to simulate. Therefore, we claim that the second regime of BO scaling is very difficult to find in numerical simulations. It would be interesting to attempt to find this regime in a shell model (Kumar & Verma Reference Kumar and Verma2015) or in some experiment.
4.2.2 Case 2: moderately stably stratified turbulence for lower wavenumbers
$(k\ll 1)$
Equations (4.3)–(4.4) indicate that
$u_{k}\approx b_{k}$
near
$k=1$
. For
$k\ll 1$
,
$\unicode[STIX]{x1D6F1}_{u}\gg \unicode[STIX]{x1D6F1}_{b}$
, implying that the dominant balance has to be between
$\unicode[STIX]{x1D6F1}_{u}$
and
$\unicode[STIX]{x1D716}$
:
$$\begin{eqnarray}\displaystyle ku_{k}^{3}\approx \unicode[STIX]{x1D716}\quad \Longrightarrow \quad u_{k}\approx \unicode[STIX]{x1D716}^{1/3}k^{-1/3}. & & \displaystyle\end{eqnarray}$$
Using (3.1),
$b_{k}$
is found to be
$$\begin{eqnarray}\displaystyle b_{k}\approx \unicode[STIX]{x1D716}^{2/3}N^{-1}k^{1/3}. & & \displaystyle\end{eqnarray}$$
With the above
$u_{k}$
and
$b_{k}$
, the evaluated energy spectra and fluxes, as well as the energy feed by buoyancy in this situation, are given by
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{u}(k)\approx \unicode[STIX]{x1D716}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6F1}_{b}(k)\approx \unicode[STIX]{x1D716}^{5/3}N^{-2}k^{4/3}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}_{B}(k)=-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}k}\unicode[STIX]{x1D6F1}_{b}(k)\approx -\frac{4}{3}\unicode[STIX]{x1D716}^{5/3}N^{-2}k^{1/3} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle E_{u}(k)\approx \unicode[STIX]{x1D716}^{2/5}k^{-5/3}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle E_{b}(k)\approx \unicode[STIX]{x1D716}^{4/3}N^{-2}k^{-1/3}. & \displaystyle\end{eqnarray}$$
$k\ll 1$
is possible in a large-aspect-ratio box, but such systems could exhibit two-dimensional or quasi-two-dimensional turbulence for which (4.1) is not valid. Hence this prediction needs to be tested thoroughly in future. Schematic diagrams exhibiting kinetic and potential energy fluxes based on the revised BO phenomenology are shown in figure 4.
Figure 4. Schematic diagram of moderately SST according to the revised BO phenomenology, which is expected in numerical simulations. (a) Kinetic energy flux and (b) potential energy flux. Energy feed rate by buoyancy (
${\mathcal{F}}_{B}(k)$
) is shown by green arrows. With
$k\lesssim 1$
and
$\unicode[STIX]{x1D6F1}_{u}(k)\approx \text{const.}$
,
$\unicode[STIX]{x1D6F1}_{b}(k)$
and
${\mathcal{F}}_{B}(k)$
increase with
$k$
as
${\sim}k^{4/3}$
and
${\sim}k^{1/3}$
, respectively. With
$k\gtrsim 1$
and
$\unicode[STIX]{x1D6F1}_{b}(k)\approx \text{const.}$
,
$\unicode[STIX]{x1D6F1}_{u}(k)$
and
${\mathcal{F}}_{B}(k)$
decrease with
$k$
as
${\sim}k^{-4/5}$
and
${\sim}k^{-9/5}$
, respectively.
5 Conclusions
In this paper, we revisit the celebrated Bolgiano–Obukhov (BO) phenomenology for SST under moderate stratification. The BO phenomenology predicts a dual scaling for the energy spectra:
$E_{u}(k)\sim k^{-11/5}$
for
$k<k_{B}$
and
$E_{u}(k)\sim k^{-5/3}$
for
$k>k_{B}$
, where
$k_{B}$
is the Bolgiano wavenumber. The potential energy varies as
${\sim}k^{-7/5}$
and
${\sim}k^{-5/3}$
, respectively, in the two regimes. The transition to
$k^{-5/3}$
scaling is based on the argument that the energy supply rate from buoyancy becomes negligible when
$k$
is large, thus making density a passive scalar (such passive scalar behaviour of density is observed in weakly stratified turbulence).
In the present paper, we start with the constancy of the total energy flux, which yields a fifth-order algebraic equation for
$u_{k}$
. Numerical solution of the above equation yields
$E_{u}(k)\sim k^{-11/5}$
and
$\unicode[STIX]{x1D6F1}_{u}(k)\sim k^{-4/5}$
, with no transition to the Kolmogorov-like scaling for larger wavenumbers. The reason behind the absence of the second scaling is that
$u_{k}$
is too weak at large wavenumbers to be able to start a constant energy cascade. The above scaling is also substantiated using asymptotic analysis.
In addition, we also derive the quantitative condition for obtaining the Kolmogorov scaling; it is given by
$k_{B}\ll k_{d}$
, where
$k_{d}$
is Kolmogorov wavenumber. This condition yields
$\unicode[STIX]{x1D716}_{u}\gg (Ri/\sqrt{Re})(U^{3}/d)$
, which may be difficult to satisfy in numerical simulations considering the fact that
$\unicode[STIX]{x1D716}_{u}\ll \unicode[STIX]{x1D716}_{b}$
. However, it may be possible that such an extreme condition for observing the second regime of BO scaling could be satisfied in some shell models of SST.
In conclusion, we believe that our revised scaling of the BO formalism for moderately stable stratification will have important consequences in the modelling of buoyancy-driven flows.
Acknowledgement
We thank S. Bhattacharya for his valuable suggestions. A.G. and M.K.V. are grateful for PLANEX/PHY/2015239, and A.G. acknowledges funding support from SERB Early Career research award ECR/2016/001493.
Open access
