Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Timokha, A.N.
and
Raynovskyy, I.A.
2017.
The damped sloshing in an upright circular tank due to an orbital forcing.
Reports of the National Academy of Sciences of Ukraine,
p.
48.
Raynovskyy, Ihor
and
Timokha, Alexander
2018.
Steady-State Resonant Sloshing in an Upright Cylindrical Container Performing a Circular Orbital Motion.
Mathematical Problems in Engineering,
Vol. 2018,
Issue. ,
p.
1.
Timokha, A.N.
2018.
Prandtl steady rotary current in an upright cylindrical container.
Reports of the National Academy of Sciences of Ukraine,
p.
45.
Ye, Wenbin
Liu, Jun
Lin, Gao
Xu, Bin
and
Yu, Long
2018.
Application of scaled boundary finite element analysis for sloshing characteristics in an annular cylindrical container with porous structures.
Engineering Analysis with Boundary Elements,
Vol. 97,
Issue. ,
p.
94.
Raynovskyy, I A
and
Timokha, A N
2018.
Damped steady-state resonant sloshing in a circular base container.
Fluid Dynamics Research,
Vol. 50,
Issue. 4,
p.
045502.
Faltinsen, Odd M.
and
Timokha, Alexander N.
2019.
An inviscid analysis of the Prandtl azimuthal mass transport during swirl-type sloshing.
Journal of Fluid Mechanics,
Vol. 865,
Issue. ,
p.
884.
Yue, Hongyuan
Chen, Jianyun
and
Xu, Qiang
2019.
Optimal design of multiple annular tuned liquid dampers for seismic reduction of 1,100-kV composite bushing.
Structural Control and Health Monitoring,
Vol. 26,
Issue. 4,
p.
e2316.
Timokha, A. N.
2019.
Nonlinear Boundary-Layer Problems and Laminar Vortical Streams Generated by Resonant Sloshing in a Tank with Circular Base.
Journal of Mathematical Sciences,
Vol. 240,
Issue. 3,
p.
358.
Gavrilyuk, I.
and
Makarov, V.
2019.
Resonant Equations with Classical Orthogonal Polynomials. I.
Ukrainian Mathematical Journal,
Vol. 71,
Issue. 2,
p.
215.
Turner, M. R.
and
Rowe, J. R.
2019.
Coupled shallow-water fluid sloshing in an upright annular vessel.
Journal of Engineering Mathematics,
Vol. 119,
Issue. 1,
p.
43.
Raynovskyy, I. A.
2019.
Steady-state resonant sloshing in upright cylindrical tank due to elliptical forcing.
Bulletin of Taras Shevchenko National University of Kyiv. Series: Physics and Mathematics,
p.
166.
Sun, Ying
Zhou, Ding
Wang, Jiadong
and
Han, Huixuan
2020.
Liquid Sloshing in a Cylindrical Tank with Multiple Baffles Under Horizontal and Pitching Motions.
International Journal of Applied Mechanics,
Vol. 12,
Issue. 07,
p.
2050080.
Love, J. S.
McNamara, K. P.
Tait, M. J.
and
Haskett, T. C.
2020.
Tuned Sloshing Dampers With Large Rectangular Core Penetrations.
Journal of Vibration and Acoustics,
Vol. 142,
Issue. 6,
Liang, Hui
Santo, Harrif
Shao, Yanlin
Law, Yun Zhi
and
Chan, Eng Soon
2020.
Liquid sloshing in an upright circular tank under periodic and transient excitations.
Physical Review Fluids,
Vol. 5,
Issue. 8,
Faltinsen, Odd M.
Lagodzinskyi, Oleksandr E.
and
Timokha, Alexander N.
2020.
Resonant three-dimensional nonlinear sloshing in a square base basin. Part 5. Three-dimensional non-parametric tank forcing.
Journal of Fluid Mechanics,
Vol. 894,
Issue. ,
Solodun, A. V.
and
Timokha, A. N.
2020.
Applied Mathematical Analysis: Theory, Methods, and Applications.
Vol. 177,
Issue. ,
p.
267.
Horstmann, G. M.
Herreman, W.
and
Weier, T.
2020.
Linear damped interfacial wave theory for an orbitally shaken upright circular cylinder.
Journal of Fluid Mechanics,
Vol. 891,
Issue. ,
Shen, Ruiyang
Lyu, Jing
and
Wang, Shimin
2021.
A variational domain decomposition scheme for the natural sloshing modes in the baffled tanks.
Journal of Sound and Vibration,
Vol. 494,
Issue. ,
p.
115855.
Tsarau, Andrei
Lugni, Claudio
Lucarelli, Alessia
Kristiansen, David
and
Lader, Pål
2021.
Sloshing in a rotating liquid inside a closed sea cage for fish farming.
Physics of Fluids,
Vol. 33,
Issue. 3,
Raynovskyy, I. A.
and
Timokha, A. N.
2021.
Damped steady-state resonant sloshing in a container of circular cross-section for arbitrary periodic nonparametric forcing.
Bulletin of Taras Shevchenko National University of Kyiv. Series: Physics and Mathematics,
p.
97.
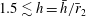 $1.5\lesssim h=\bar{h}/\bar{r}_{2}$) and away from the non-dimensional inner radii
$1.5\lesssim h=\bar{h}/\bar{r}_{2}$) and away from the non-dimensional inner radii 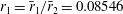 $r_{1}=\bar{r}_{1}/\bar{r}_{2}=0.08546$, 0.17618, 0.27826, 0.31323, 0.31855, 0.43444, 0.46015, 0.48434, 0.68655, 0.70118. The theory is used to describe steady-state (stable and unstable) resonant waves due to a harmonic excitation with the forcing frequency close to the lowest natural sloshing frequency. We show that the surge-sway-pitch-roll excitation is always of either longitudinal or elliptic type. Existing experimental results on the horizontally excited steady-state wave regimes in an upright circular tank (
$r_{1}=\bar{r}_{1}/\bar{r}_{2}=0.08546$, 0.17618, 0.27826, 0.31323, 0.31855, 0.43444, 0.46015, 0.48434, 0.68655, 0.70118. The theory is used to describe steady-state (stable and unstable) resonant waves due to a harmonic excitation with the forcing frequency close to the lowest natural sloshing frequency. We show that the surge-sway-pitch-roll excitation is always of either longitudinal or elliptic type. Existing experimental results on the horizontally excited steady-state wave regimes in an upright circular tank (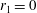 $r_{1}=0$) are utilised for validation. Inserting an inner pole with the radii
$r_{1}=0$) are utilised for validation. Inserting an inner pole with the radii 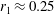 $r_{1}\approx 0.25$ and 0.35 (
$r_{1}\approx 0.25$ and 0.35 (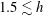 $1.5\lesssim h$) causes that no stable swirling and/or irregular waves exist. The response curves for an elliptic-type excitation are examined versus the minor-axis forcing-amplitude component. Stable swirling is then expected being co- and counter-directed to the angular forcing direction. Passage to the rotary (circular) excitation keeps the co-directed swirling stable for all resonant forcing frequencies but the stable counter-directed swirling disappears.
$1.5\lesssim h$) causes that no stable swirling and/or irregular waves exist. The response curves for an elliptic-type excitation are examined versus the minor-axis forcing-amplitude component. Stable swirling is then expected being co- and counter-directed to the angular forcing direction. Passage to the rotary (circular) excitation keeps the co-directed swirling stable for all resonant forcing frequencies but the stable counter-directed swirling disappears.