Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T16:40:43.790Z Has data issue: false hasContentIssue false
  • English
  • Français

Radiofrequency plasma stabilization of a low-Reynolds-number channel flow

Published online by Cambridge University Press:  08 May 2014

Timothy J. Fuller ,
Andrea G. Hsu ,
Rodrigo Sanchez-Gonzalez ,
Jacob C. Dean ,
Simon W. North  and
Rodney D. W. Bowersox
Timothy J. Fuller
Affiliation:
Aerospace Engineering, Texas A&M University, College Station, TX 77843, USA
Andrea G. Hsu
Affiliation:
Chemistry, Texas A&M University, College Station, TX 77843, USA
Rodrigo Sanchez-Gonzalez
Affiliation:
Chemistry, Texas A&M University, College Station, TX 77843, USA
Jacob C. Dean
Affiliation:
Chemistry, Texas A&M University, College Station, TX 77843, USA
Simon W. North
Affiliation:
Chemistry, Texas A&M University, College Station, TX 77843, USA
Rodney D. W. Bowersox*
Affiliation:
Aerospace Engineering, Texas A&M University, College Station, TX 77843, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

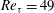The effects of plasma heating and thermal non-equilibrium on the statistical properties of a low-Reynolds-number ($Re_{\tau } = 49$) turbulent channel flow were experimentally quantified using particle image velocimetry, two-line planar laser-induced fluorescence, coherent anti-Stokes Raman spectroscopy and emission spectroscopy. Tests were conducted at two radiofrequency plasma settings. The nitrogen, in air, was vibrationally excited to 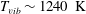$T_{vib} \sim 1240\ \mathrm{K}$ and 1550 K for 150 W and 300 W plasma settings, respectively, while the vibrational temperature of the oxygen and the rotational/translational temperatures of all species remained near room temperature. The peak axial turbulence intensities in the shear layers were reduced by 15 and 30 % in moving across the plasma for the 150 and 300 W cases, respectively. The plasma did not alter the transverse intensities. The Reynolds shear stresses were reduced by 30 and 50 % for the 150 and 300 W cases. The corresponding Reynolds shear stress correlation coefficient was also reduced, which indicates that the large-scale structures were diminished. Finally, the plasma enhanced the turbulence decay in the zero-shear regions, where the power law decay 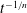$t^{-1/n}$ exponential factor $n$ decreased from 1.0 to 0.8.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows MHD and Electrohydrodynamics: Plasmas Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 748 , 10 June 2014 , pp. 663 - 691
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aleksandrov, A. F., Vidiakin, N. G., Lakutin, V. A., Skvortsov, M. G. & Timofeev, I. B. 1986 A possible mechanism for interaction of a shock wave with a decaying laser plasma in air. Sov. Phys. Tech. Phys. 31 (4), 468–469.Google Scholar
Allen, J. 1992 Probe theory – the orbital motion approach. Phys. Scr. 45 (5), 497–503.Google Scholar
Arnette, S., Samimy, M. & Elliott, G. 1998 The effects of expansion on the turbulence structure of compressible boundary layers. J. Fluid Mech. 367, 67–105.Google Scholar
Barnes, M., Keller, J., Forster, J., O’Neil, J. & Coutlas, D. 1992 Transport of dust particles in glow-discharge plasmas. Phys. Rev. Lett. 68, 313–316.Google Scholar
Bass, H. 1981 Absorption of sound by air: high temperature predictions. J. Acoust. Soc. Am. 69 (1), 124–138.Google Scholar
Batchelor, G. & Townsend, A. 1948 Decay of isotropic turbulence in the initial period. Proc. R. Soc. Lond. A 193, 539–558.Google Scholar
Benedict, L. & Gould, R. 1996 Towards better uncertainty estimates for turbulence statistics. Exp. Fluids 22, 129–136.Google Scholar
Biskamp, D. 1993 Nonlinear Magnetohydrodynamics. Cambridge University Press.Google Scholar
Biskamp, D. 2000 Magnetic Reconnection in Plasmas. Cambridge University Press.CrossRefGoogle Scholar
Biskamp, D. 2003 Magnetohydrodynamic Turbulence. Cambridge University Press.Google Scholar
Boeuf, J. & Punset, C. 1999 Physics and modeling of dusty plasma. In Dusty Plasmas (ed. Bouchoule, A.), chap. 1. John Wiley and Sons.Google Scholar
Bowersox, R. D. W. 2009 Extension of equilibrium turbulent heat flux models to high-speed shear flows. J. Fluid Mech. 633, 61–70.Google Scholar
Bradshaw, P. 1969 The analogy between streamline curvature and buoyancy in turbulent shear flow. J. Fluid Mech. 36, 177–191.Google Scholar
Bradshaw, P.1973 The effect of streamline curvature on turbulent flow, AGARD-AG-169, NATO Science and Technology Organization.Google Scholar
Brennan, M., Alle, D., Euripides, P., Buckman, S. & Brunger, M. 1992 Elastic electron scattering and rovibrational excitation of ${\rm N_{2}}$ at low incident energies. J. Phys. B: At. Mol. Opt. Phys. 25, 2669–2682.Google Scholar
Cattolica, R. 1981 OH rotational temperature from two-line laser-excited fluorescence. Appl. Opt. 20, 1156–1166.Google Scholar
Chen, C. & Blackwelder, R. 1978 Large-scale motion in a turbulent boundary layer: a study using temperature contamination. J. Fluid Mech. 89, 1–31.Google Scholar
Chen, Q., Chen, S. & Eyink, G. 2003 The joint cascade of energy and helicity in three-dimensional turbulence. Phys. Fluids 15 (2), 361–374.Google Scholar
Cho, J. 2011 Magnetic helicity conservation and inverse energy cascade in electron magnetohydrodynamic wavepackets. Phys. Rev. Lett. 106, 191104-1–191104-4.Google Scholar
Christensen, K. & Adrian, R. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.Google Scholar
Dussauge, J. P. & Gaviglio, J. 1987 The rapid expansion of a supersonic turbulent flow: role of bulk dilatation. J. Fluid Mech. 174, 81–112.Google Scholar
Ekoto, I., Bowersox, R. D. W., Beutner, T. & Goss, L. 2009 Response of supersonic turbulent boundary layers to local and global mechanical distortions. J. Fluid Mech. 630, 225–265.Google Scholar
Evtyukhin, N. V., Margolin, A. D. & Shmelev, V. M. 1986 On the nature of shock wave acceleration in glow discharge plasma. Sov. J. Chem. Phys. 3, 2080–2089.Google Scholar
Falgarone, E. & Passot, T.(Eds) 2003 Turbulence and Magnetic Field in Astrophysics, Lect. Notes Physics. Springer, Berlin.Google Scholar
Fujii, K. & Hornung, H. 2003 Experimental investigation of high-enthalpy effects on attachment-line boundary-layer transition. AIAA J. 41 (7), 1282–1291.Google Scholar
Galtier, S. & Bhattacharjee, A. 2003 Anisotropic weak whistler wave turbulence in electron magnetohydrodynamics. Phys. Plasmas 10 (8), 3065–3076.Google Scholar
Hanson, R. K. 1988 Planar laser-induced fluorescence imaging. J. Quant. Spectrosc. Radiat. Transfer 40, 343–362.Google Scholar
Huang, M.-J. & Leonard, A. 1994 Power-law decay of homogeneous turbulence at low Reynolds numbers. Phys. Fluids 6, 3765–3775.Google Scholar
Hussain, A. & Reynolds, W. 1975 Measurement in a fully developed channel flow. Trans. ASME, J. Fluids Engrs 97 (4), 68–78.Google Scholar
Ionikh, Y., Chernysheva, N., Meshchanov, A., Yalin, A. & Miles, R. 1999 Direct evidence or thermal mechanism of plasma influence on shock wave propagation. Phys. Lett. A 259, 387–392.Google Scholar
Itikawa, Y., Hayashi, M., Ichimura, A., Onda, K., Sakimoto, K., Takayanagi, K., Nakamura, M., Nishimura, H. & Takayanagi, T. 1986 Cross-sections for collisions of electrons and photons with nitrogen molecules. J. Phys. Chem. Ref. Data 15 (3), 985–1010.Google Scholar
Itikawa, Y., Ichimaru, A., Onda, K., Sakimoto, K., Takayanagi, K., Hatano, Y., Hayashi, M., Nishimura, H. & Tsurubuchi, S. 1989 Cross-sections for collisions of electrons and photons with oxygen molecules. J. Phys. Chem. Ref. Data 18 (9), 23–42.Google Scholar
Kim, H., Kline, S. & Reynolds, W. 1971 The production of turbulence near a smooth wall in a turbulent boundary layer. J. Fluid Mech. 50, 133–160.Google Scholar
Klimov, A., Koblov, A., Mishin, G., Serov, Y. & Yavor, I. 1982 Shock wave propagation in a glow discharge. Sov. Phys. Tech. Phys. 8 (4), 192–194.Google Scholar
Kline, S., Reynolds, W., Schraub, F. & Runstadler, P. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Landau, L. & Teller, E. 1936 Zur theorie der schalldispersion. Phys. Z. Sowjetunion 10 (1), 34.Google Scholar
Launder, B., Reece, G. & Rodi, W. 1975 Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 68 (3), 537–566.Google Scholar
Leyva, I., Jewell, J., Laurence, S., Hornung, H. & Shepherd, J.2009 On the impact of injection schemes on transition in hypersonic boundary layers, AIAA Paper 2009-7204.Google Scholar
Loth, E. 2008 Compressibility and rarefaction effects on drag of a spherical particle. AIAA J. 46, 2219–2228.Google Scholar
Lucht, R. P. 1987 Three-laser coherent anti-Stokes Raman scattering measurements of two species. Opt. Lett. 12 (2), 78–80.Google Scholar
Luker, J., Bowersox, R. D. W. & Buter, T. 2000 Influence of a curvature driven favorable pressure gradient on a supersonic turbulent boundary layer. AIAA J. 38 (8), 1351–1359.Google Scholar
Macheret, S. O., Ionikh, Y. Z., Chernysheva, N. V., Yalin, A. P., Martinelli, L. & Miles, R. B. 2001 Shock wave propagation and dispersion in glow discharge plasmas. Phys. Fluids 13 (9), 2693–2705.Google Scholar
Maden, I., Maduta, R., Kriegseis, J., Jakirlic, S., Schwarz, C., Grundmann, S. & Tropea, C. 2013 Experimental and computational study of the flow induced by a plasma. Intl J. Heat Fluid Flow 41, 80–89.Google Scholar
Martin, M. P. & Candler, G. V. 1998 Effect of chemical reactions on decaying isotropic turbulence. Phys. Fluids 10 (7), 1715–1724.Google Scholar
Matsoukas, T. & Russell, M. 1995 Particle charging in low-pressure plasmas. J. Appl. Phys. 77, 4285–4292.Google Scholar
McMillin, B., Palmer, J. & Hanson, R. 1993 Temporally resolved, two-line fluorescence imaging of NO temperature in a transverse jet in a supersonic cross flow. Appl. Opt. 32, 7532–7545.Google Scholar
Menon, R. & Lai, W. 1991 Key considerations in the selection of seed particles for LDV measurements. In 4th Int. Conf. on Laser Anemometry, TSI Inc.Google Scholar
Merriman, S., Ploenjes, E., Palm, P. & Adamovich, I. 2001 Shock wave control by nonequilibrium plasmas in cold supersonic gas flows. AIAA J. 39 (8), 1547–1552.Google Scholar
Montello, A., Nishihara, M., Rich, W., Adamovich, I. & Lempert, W. 2012 Nitrogen vibrational population measurements in the plenum of a hypersonic wind tunnel. AIAA J. 50, 1368–1376.Google Scholar
Mott-Smith, H. & Langmuir, I. 1926 The theory of collectors in gaseous discharges. Phys. Rev. 28 (4), 727–763.Google Scholar
Nakanishi, R., Mamori, H. & Fukagata, K. 2012 Relaminarization of turbulent channel flow using wave-like wall deformations. Intl J. Heat Fluid Flow 35, 152–159.Google Scholar
Narasimha, R. & Sreenivasan, K. R. 1979 Relaminarization of fluid flows. Adv. Appl. Mech. 19, 221–309.Google Scholar
Narayanan, B. 1968 An experimental study of reverse transition in two-dimensional channel flow. J. Fluid Mech. 31 (part 3), 609–623.Google Scholar
Nicholl, C. 1970 Some dynamical effects of heat on a boundary layer. J. Fluid Mech. 40 (2), 361–384.Google Scholar
Osipov, A., Uvarov, A. & Vinnichenko, N. 2006 Influence of the initial vibrationally non-equilibrium state of a medium on the structure of von Karman vortex sheet. Phys. Fluids 18, 1–7.Google Scholar
Palm, P., Meyer, R., Plonjes, E., Rich, J. & Adamovich, I. 2003 Nonequilibrium radio frequency discharge plasma effect on conical shock wave: $M = 2.5$ flow. AIAA J. 41 (3), 465–469.Google Scholar
Palmer, R.1989 The CARSFIT computer code for calculating coherent anti-Stokes Raman spectra: user and programmer information, Sandia Report SAND89-8206, Sandia National Laboratories, Livermore, CA.Google Scholar
Panton, R. 1997 Self-Sustaining Mechanisms of Wall Turbulence. Computational Mechanics Publications.Google Scholar
Patel, V. 1965 Calibration of the Preston tube and limitations on its use in pressure gradients. J. Fluid Mech. 23, 185–208.Google Scholar
Patel, V. & Head, M. 1968 Reversion of turbulent to laminar flow. J. Fluid Mech. 34 (2), 371–392.Google Scholar
Raizer, Y. 1997 Gas Discharge Physics. Springer.Google Scholar
Robinson, S. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601–639.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Shapiro, A. 1953 The Dynamics and Thermodynamics of Compressible Flow. vol. 1. chap. 8. pp. 219–260. John Wiley & Sons.Google Scholar
Shukla, P. & Mamun, A. 2002 Introduction to Dusty Plasma. Institute of Physics Publishing.Google Scholar
Spina, E. F., Smits, A. J. & Robinson, S. 1994 The physics of supersonic turbulent boundary layers. Annu. Rev. Fluid Mech. 26, 287–319.Google Scholar
Sreenivasan, K. R. 1982 Review article laminarescent, relaminarizing and retransitional flow. Acta Mechanica 44, 1–48.Google Scholar
Stanfield, S. A., James Menart, DeJoseph. C. Jr, Kimmel, R. L. & Hayes, J. R. 2009 Rotational and vibrational temperature distributions for a dielectric barrier discharge in air. AIAA J. 47 (5), 1107–1115.Google Scholar
Theodorsen, T.1952 Mechanism of turbulence, Proc. 2nd Midwestern Conf. Fluid Mechanics, Ohio State University, Columbus, Ohio, pp. 1–19.Google Scholar
Tichenor, N., Humble, R. & Bowersox, R. D. W. 2013 Response of hypersonic turbulent boundary layer to favorable pressure gradients. J. Fluid Mech. 722, 187–213.Google Scholar
Trevisan, C., Houfek, K., Zhang, Z., Orel, A., McCurdy, C. & Rescigno, R. 2005 Nonlocal model of dissociative electron attachment and vibrational excitation of NO. Phys. Rev. A 71, 052714.Google Scholar
Tsukahara, T., Seki, Y., Kawamura, H. & Tochio, D. 2004 DNS of turbulent channel flow with very low Reynolds numbers. In Comp. Mech., WCCM VI, APCOM’04 Beijing, China, Sept. 5–10, Tsinghua University Press & Springer.Google Scholar
Vedenov, A. A. 1968 Theory of Turbulent Plasma. London Iliffe Book Ltd.Google Scholar
Verma, M. K. 2004 Statistical theory of magnetohydrodynamic turbulence: recent results. Phys. Rep. 401, 229–380.CrossRefGoogle Scholar
Voinovich, P. A., Ershov, A. P., Ponomareva, S. E. & Shibkov, V. M. 1991 Propagation of weak shock waves in plasma of longitudinal glow discharge in air. High Temp. 29, 468–475.Google Scholar
Wilcox, D. 2000 Turbulence Modeling for CFD. DCW Ind.Google Scholar
Zhu, J.-Z., Yang, W. & Zhu, G.-Y. 2014 Purely helical absolute equilibria and chirality of (magneto) fluid turbulence. J. Fluid Mech. 739, 479–501.Google Scholar