Published online by Cambridge University Press: 04 April 2018
Passive scalar transport in turbulent channel flow subject to spanwise system rotation is studied by direct numerical simulations. The Reynolds number 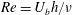 $Re=U_{b}h/\unicode[STIX]{x1D708}$ is fixed at 20 000 and the rotation number
$Re=U_{b}h/\unicode[STIX]{x1D708}$ is fixed at 20 000 and the rotation number 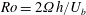 $Ro=2\unicode[STIX]{x1D6FA}h/U_{b}$ is varied from 0 to 1.2, where
$Ro=2\unicode[STIX]{x1D6FA}h/U_{b}$ is varied from 0 to 1.2, where 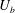 $U_{b}$ is the bulk mean velocity,
$U_{b}$ is the bulk mean velocity, 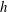 $h$ the half channel gap width and
$h$ the half channel gap width and 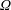 $\unicode[STIX]{x1D6FA}$ the rotation rate. The scalar is constant but different at the two walls, leading to steady scalar transport across the channel. The rotation causes an unstable channel side with relatively strong turbulence and turbulent scalar transport, and a stable channel side with relatively weak turbulence or laminar-like flow, weak turbulent scalar transport but large scalar fluctuations and steep mean scalar gradients. The distinct turbulent–laminar patterns observed at certain
$\unicode[STIX]{x1D6FA}$ the rotation rate. The scalar is constant but different at the two walls, leading to steady scalar transport across the channel. The rotation causes an unstable channel side with relatively strong turbulence and turbulent scalar transport, and a stable channel side with relatively weak turbulence or laminar-like flow, weak turbulent scalar transport but large scalar fluctuations and steep mean scalar gradients. The distinct turbulent–laminar patterns observed at certain 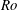 $Ro$ on the stable channel side induce similar patterns in the scalar field. The main conclusions of the study are that rotation reduces the similarity between the scalar and velocity field and that the Reynolds analogy for scalar-momentum transport does not hold for rotating turbulent channel flow. This is shown by a reduced correlation between velocity and scalar fluctuations, and a strongly reduced turbulent Prandtl number of less than 0.2 on the unstable channel side away from the wall at higher
$Ro$ on the stable channel side induce similar patterns in the scalar field. The main conclusions of the study are that rotation reduces the similarity between the scalar and velocity field and that the Reynolds analogy for scalar-momentum transport does not hold for rotating turbulent channel flow. This is shown by a reduced correlation between velocity and scalar fluctuations, and a strongly reduced turbulent Prandtl number of less than 0.2 on the unstable channel side away from the wall at higher 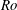 $Ro$. On the unstable channel side, scalar scales become larger than turbulence scales according to spectra and the turbulent scalar flux vector becomes more aligned with the mean scalar gradient owing to rotation. Budgets in the governing equations of the scalar energy and scalar fluxes are presented and discussed as well as other statistics relevant for turbulence modelling.
$Ro$. On the unstable channel side, scalar scales become larger than turbulence scales according to spectra and the turbulent scalar flux vector becomes more aligned with the mean scalar gradient owing to rotation. Budgets in the governing equations of the scalar energy and scalar fluxes are presented and discussed as well as other statistics relevant for turbulence modelling.