Published online by Cambridge University Press: 01 March 2018
Recent experiments have revealed the existence of very long streamwise features, denoted as very-large-scale motions (VLSMs), in the thermally neutral atmospheric boundary layer (ABL) (Hutchins et al., Boundary-Layer Meteorol., vol. 145(2), 2012, pp. 273–306). The aim of our study is to elaborate the role of these large-scale anisotropic patterns in wind-energy harvesting with special emphasis on the organization of turbulent fields around wind turbines. To this end, we perform large-eddy simulation (LES) of a turbine row operating under neutral conditions. The ABL data are produced separately in a very long domain of 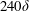 $240\unicode[STIX]{x1D6FF}$, where
$240\unicode[STIX]{x1D6FF}$, where  $\unicode[STIX]{x1D6FF}$ is the ABL thickness, to ensure a realistic representation for very large scales of
$\unicode[STIX]{x1D6FF}$ is the ABL thickness, to ensure a realistic representation for very large scales of  $O(10\unicode[STIX]{x1D6FF})$. VLSMs are extracted from the LES database using a cutoff at streamwise wavelength
$O(10\unicode[STIX]{x1D6FF})$. VLSMs are extracted from the LES database using a cutoff at streamwise wavelength 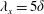 $\unicode[STIX]{x1D706}_{x}=5\unicode[STIX]{x1D6FF}$, or
$\unicode[STIX]{x1D706}_{x}=5\unicode[STIX]{x1D6FF}$, or 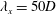 $\unicode[STIX]{x1D706}_{x}=50D$ in terms of turbine diameter. Reynolds averaging of low-pass filtered fields shows that the interaction of VLSMs and turbines produce very-long-wavelength motions in the wake region, which contain approximately
$\unicode[STIX]{x1D706}_{x}=50D$ in terms of turbine diameter. Reynolds averaging of low-pass filtered fields shows that the interaction of VLSMs and turbines produce very-long-wavelength motions in the wake region, which contain approximately 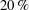 $20\,\%$ of the resolved Reynolds shear stress, and
$20\,\%$ of the resolved Reynolds shear stress, and 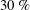 $30\,\%$ of the resolved streamwise kinetic energy in the shear layers. To further elucidate these statistics, we conduct a geometrical analysis using conditional averaging based on large-scale low- and high-velocity events. The conditional eddies provide evidence for very long (
$30\,\%$ of the resolved streamwise kinetic energy in the shear layers. To further elucidate these statistics, we conduct a geometrical analysis using conditional averaging based on large-scale low- and high-velocity events. The conditional eddies provide evidence for very long (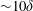 ${\sim}10\unicode[STIX]{x1D6FF}$) and wide (
${\sim}10\unicode[STIX]{x1D6FF}$) and wide (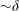 ${\sim}\unicode[STIX]{x1D6FF}$) streak–roller structures around the turbine row. Although all of these eddies share the same streak–roller topology, there are remarkable modifications in the morphology of the conditional eddies whose cores are located sideways to the turbines. In these cases, the turbine row pushes the whole low- or high-momentum streak aside, and prevails as a sharp boundary to the low–high-momentum streak pair. In this process, accompanying rollers remain relatively unaffected. This creates a two-way flux towards the turbine row. These observations provide some insights about the high lateral spreading observed in the large-scale Reynolds stress fields.
${\sim}\unicode[STIX]{x1D6FF}$) streak–roller structures around the turbine row. Although all of these eddies share the same streak–roller topology, there are remarkable modifications in the morphology of the conditional eddies whose cores are located sideways to the turbines. In these cases, the turbine row pushes the whole low- or high-momentum streak aside, and prevails as a sharp boundary to the low–high-momentum streak pair. In this process, accompanying rollers remain relatively unaffected. This creates a two-way flux towards the turbine row. These observations provide some insights about the high lateral spreading observed in the large-scale Reynolds stress fields.