1. Introduction
After introducing the concept of mean iso-surface area density ![]() $\varSigma$ to describe the mean reaction rate of a diffusion flame, Marble & Broadwell (Reference Marble and Broadwell1977) proposed a differential equation for
$\varSigma$ to describe the mean reaction rate of a diffusion flame, Marble & Broadwell (Reference Marble and Broadwell1977) proposed a differential equation for ![]() $\partial \varSigma /\partial t$ based on phenomenological arguments that captured many of the important physics of flame propagation. Subsequent studies proposed exact formulations for
$\partial \varSigma /\partial t$ based on phenomenological arguments that captured many of the important physics of flame propagation. Subsequent studies proposed exact formulations for ![]() $\varSigma$ and its transport equation for arbitrary propagating surfaces in turbulence (Pope Reference Pope1988), as well as premixed flames (Trouvé Reference Trouvé1994; Trouvé & Poinsot Reference Trouvé and Poinsot1994) and non-premixed flames (van Kalmthout, Veynante & Candel Reference van Kalmthout, Veynante and Candel1996; van Kalmthout & Veynante Reference van Kalmthout and Veynante1998). Studies by Candel & Poinsot (Reference Candel and Poinsot1990), Kollmann & Chen (Reference Kollmann and Chen1994) and Vervisch et al. (Reference Vervisch, Bidaux, Bray and Kollmann1995) helped to codify the relationship between the surface area of a level set and the flame surface area.
$\varSigma$ and its transport equation for arbitrary propagating surfaces in turbulence (Pope Reference Pope1988), as well as premixed flames (Trouvé Reference Trouvé1994; Trouvé & Poinsot Reference Trouvé and Poinsot1994) and non-premixed flames (van Kalmthout, Veynante & Candel Reference van Kalmthout, Veynante and Candel1996; van Kalmthout & Veynante Reference van Kalmthout and Veynante1998). Studies by Candel & Poinsot (Reference Candel and Poinsot1990), Kollmann & Chen (Reference Kollmann and Chen1994) and Vervisch et al. (Reference Vervisch, Bidaux, Bray and Kollmann1995) helped to codify the relationship between the surface area of a level set and the flame surface area.
Although the iso-surface area density formalism was initially conceived for infinitesimally thin, coherent flames, the subsequent transport equation for the surface area of an iso-level of a scalar field is exact and does not require the concept of a coherent flame to be valid. In fact, a wide range of turbulent mixing problems can be studied with this method as long as the interface can be defined by a constant value of a scalar field, e.g. the stoichiometric value of the mixture fraction in non-premixed combustion (Peters Reference Peters1988), the value of a progress variable (i.e. temperature or species mass fraction) corresponding to the peak reaction rate in premixed combustion (Candel & Poinsot Reference Candel and Poinsot1990), or a suitably ‘small’ value of the mean square vorticity for the turbulent/non-turbulent interface (da Silva et al. Reference da Silva, Hunt, Eames and Westerweel2014), among others.
Early studies established that the rate of iso-surface area production is driven by the tangential strain rate (Fichot et al. Reference Fichot, Delhaye, Veynante and Candel1994) and the preferential alignment of the scalar gradient with the most compressive eigenvector of the strain rate tensor (Ashurst et al. Reference Ashurst, Kerstein, Kerr and Gibson1987), provided that the rate of heat release (and flow dilatation) is small (Kim & Pitsch Reference Kim and Pitsch2007). The rate of iso-surface area destruction was found to be due to the combined effects of the curvature and the propagation velocity of the surface; for passive scalars, the propagation velocity is due to molecular diffusion, whereas the propagation of a premixed flame is strongly influenced by chemical reactions (Vervisch & Poinsot Reference Vervisch and Poinsot1998). The statistical behaviour of the surface curvature and propagation term has received significant attention (Chakraborty & Cant Reference Chakraborty and Cant2005, Reference Chakraborty and Cant2013). Recent results from Dopazo et al. (Reference Dopazo, Martin, Cifuentes and Hierro2018) suggest that the propagation velocity of the iso-surface affects both the destruction and the production terms, making the effect of propagation speed on iso-surface transport difficult to isolate.
A key finding in several studies of iso-surface transport is that the rate of change of the iso-surface area is significantly smaller in magnitude than the production and destruction terms. A notable example is the study by Han & Huh (Reference Han and Huh2008), in which a premixed flame evolving in homogeneous, decaying turbulence is examined. Here, the temporal evolution of the flame surface area, as well as the production and destruction terms of the surface transport equation, are presented for a range of Lewis numbers. Blakeley, Wang & Riley (Reference Blakeley, Wang and Riley2019) performed a similar analysis for a passive scalar field evolving in decaying, isotropic turbulence. In this study, the evolution of iso-surface area and the transport terms were compared for two different initial scalar distributions. Recently, two studies examined the variation of flame surface area and transport along the axis of a premixed jet flame (Wang et al. Reference Wang, Hawkes, Chen, Zhou, Li and Aldén2017; Luca et al. Reference Luca, Attili, Schiavo, Creta and Bisetti2019).
In a recent study of spherically expanding premixed flames, Kulkarni & Bisetti (Reference Kulkarni and Bisetti2021) examined the evolution of the peak value of mean flame surface area density, ![]() $\varSigma _{max}$, as a function of time and Reynolds number. The resulting analysis suggested that primary contributions to the rate of change of
$\varSigma _{max}$, as a function of time and Reynolds number. The resulting analysis suggested that primary contributions to the rate of change of ![]() $\varSigma _{max}$ include: the mean velocity field, found to scale with the pressure rise of the flame; the turbulent velocity field, found to scale with the integral length of the flow,
$\varSigma _{max}$ include: the mean velocity field, found to scale with the pressure rise of the flame; the turbulent velocity field, found to scale with the integral length of the flow, ![]() $\ell$; and the net surface ‘stretch’ (i.e. the net effect from the production and destruction terms), found to scale with the Kolmogorov length,
$\ell$; and the net surface ‘stretch’ (i.e. the net effect from the production and destruction terms), found to scale with the Kolmogorov length, ![]() $\eta$.
$\eta$.
Blakeley, Olson & Riley (Reference Blakeley, Olson and Riley2022) performed a direct numerical simulation (DNS) of a passive scalar field in a turbulent, temporally developing shear layer, and found that cross-stream profiles of the mean iso-surface area density evolve in a self-similar manner when normalized by the scalar Taylor length scale ![]() $\lambda _\phi$. The present study is an extension to this work, which will focus on the transport equation for
$\lambda _\phi$. The present study is an extension to this work, which will focus on the transport equation for ![]() $\varSigma$, and examine the orders of magnitude and self-similar scalings of each term. In § 2, the governing equations and numerical methods used to simulate the constant density temporal mixing layer are discussed. The iso-surface transport equation, and the numerical methods used to approximate the terms, are discussed in § 3. A brief overview of the self-similar behaviour of the mixing layer examined in this study is given in § 4. The main results of the current study are presented in §§ 5–7, which address the balance of the
$\varSigma$, and examine the orders of magnitude and self-similar scalings of each term. In § 2, the governing equations and numerical methods used to simulate the constant density temporal mixing layer are discussed. The iso-surface transport equation, and the numerical methods used to approximate the terms, are discussed in § 3. A brief overview of the self-similar behaviour of the mixing layer examined in this study is given in § 4. The main results of the current study are presented in §§ 5–7, which address the balance of the ![]() $\varSigma$ transport equation, the self-similar scalings of each term, and some physical interpretations of the terms. Finally, in § 8, the key results from this study are summarized and future research trajectories are proposed.
$\varSigma$ transport equation, the self-similar scalings of each term, and some physical interpretations of the terms. Finally, in § 8, the key results from this study are summarized and future research trajectories are proposed.
2. Direct numerical simulation
The DNS used for the present study was described in detail by Blakeley et al. (Reference Blakeley, Olson and Riley2022); a brief description will be given here. For more details, please refer to the previous work.
2.1. Numerical methods and simulation parameters
The DNS discussed herein was generated using the ‘Miranda’ codebase, which has been employed in the past to investigate fundamental problems in turbulent mixing, such as the Rayleigh–Taylor and Richtmyer–Meshkov instabilities, among others (Cabot & Cook Reference Cabot and Cook2006; Olson et al. Reference Olson, Larsson, Lele and Cook2011; Tritschler et al. Reference Tritschler, Olson, Lele, Hickel, Hu and Adams2014). Miranda is formulated as an artificial large eddy simulation, which forgoes an explicit subgrid scale model in favour of dynamic fluid properties (e.g. viscosity, molecular diffusivity) that act only in the regions of steepest gradients (Cook Reference Cook2007). For the present simulation, the fluid diffusivities (namely viscosity, thermal conductivity and scalar diffusivity) are set to constant values. By ensuring that the smallest scales of flow are resolved by the grid spacing, the simulation discussed is a DNS.
Miranda solves the three-dimensional, compressible equations for conservation of mass (![]() $\rho$), momentum (
$\rho$), momentum (![]() $\rho U_i$), energy (
$\rho U_i$), energy (![]() $E$) and scalar concentration (
$E$) and scalar concentration (![]() $\rho \varPhi$). Spatial derivatives are approximated with a tenth-order, compact finite difference scheme (Lele Reference Lele1992), and temporal integration is performed with a low-storage, five-stage, fourth-order Runge–Kutta scheme (Kennedy, Carpenter & Lewis Reference Kennedy, Carpenter and Lewis2000). An eighth-order compact filter, designed to remove approximately the top 10 % of wavenumbers, is used to dealias the solution at each time step. An adaptive time step, accounting for both advective and acoustic time scales, ensures proper temporal resolution and numerical stability. Interested readers are encouraged to consult Cook (Reference Cook2007, Reference Cook2009) for additional information on the code formulation.
$\rho \varPhi$). Spatial derivatives are approximated with a tenth-order, compact finite difference scheme (Lele Reference Lele1992), and temporal integration is performed with a low-storage, five-stage, fourth-order Runge–Kutta scheme (Kennedy, Carpenter & Lewis Reference Kennedy, Carpenter and Lewis2000). An eighth-order compact filter, designed to remove approximately the top 10 % of wavenumbers, is used to dealias the solution at each time step. An adaptive time step, accounting for both advective and acoustic time scales, ensures proper temporal resolution and numerical stability. Interested readers are encouraged to consult Cook (Reference Cook2007, Reference Cook2009) for additional information on the code formulation.
This study is part of an ongoing project to port established computing software to heterogeneous architectures containing both traditional CPUs and graphics processing units (GPUs) at Lawrence Livermore National Laboratory (LLNL). More information regarding the GPU porting process can be found in the technical report by Anderson et al. (Reference Anderson2020).
The simulation presented herein is a canonical temporal mixing layer, with the initial mean velocity and passive scalar profiles initialized with the hyperbolic tangent function. The size of the computational domain is ![]() $L_x=1600\delta _0\times L_y=600\delta _0\times L_z=400\delta _0$, which is discretized by
$L_x=1600\delta _0\times L_y=600\delta _0\times L_z=400\delta _0$, which is discretized by ![]() $4096\times 1536\times 1024$ (6.4 billion) grid points, and
$4096\times 1536\times 1024$ (6.4 billion) grid points, and ![]() $\Delta x = \Delta y = \Delta z$. Boundary conditions are periodic in the
$\Delta x = \Delta y = \Delta z$. Boundary conditions are periodic in the ![]() $x,z$ (streamwise, spanwise) directions, with free-slip boundary in the
$x,z$ (streamwise, spanwise) directions, with free-slip boundary in the ![]() $y$ (cross-stream) direction.
$y$ (cross-stream) direction.
The initial Reynolds number based on the momentum thickness is ![]() ${Re}_{\delta _0} = \Delta U \delta _0/\upsilon = 120$, and the Schmidt and Prandtl numbers (for the passive scalar and thermal diffusivities) are set to
${Re}_{\delta _0} = \Delta U \delta _0/\upsilon = 120$, and the Schmidt and Prandtl numbers (for the passive scalar and thermal diffusivities) are set to ![]() $Sc=Pr=0.7$ to approximate atmospheric conditions. Homogeneous, isotropic velocity fluctuations are imposed on the mean velocity field to promote the growth of unstable modes and transition to turbulence; no fluctuations are added the mean scalar field. The convective Mach number
$Sc=Pr=0.7$ to approximate atmospheric conditions. Homogeneous, isotropic velocity fluctuations are imposed on the mean velocity field to promote the growth of unstable modes and transition to turbulence; no fluctuations are added the mean scalar field. The convective Mach number ![]() $Ma = c_s/\Delta U$ is 0.15, such that compressibility effects can be neglected safely, and the fluid is effectively isothermal and incompressible.
$Ma = c_s/\Delta U$ is 0.15, such that compressibility effects can be neglected safely, and the fluid is effectively isothermal and incompressible.
In this configuration, the flow is statistically homogeneous in the ![]() $x,z$ directions, which implies that for any quantity
$x,z$ directions, which implies that for any quantity ![]() $Q$,
$Q$, ![]() $\partial \langle Q\rangle /\partial x = \partial \langle Q\rangle /\partial z = 0$, where
$\partial \langle Q\rangle /\partial x = \partial \langle Q\rangle /\partial z = 0$, where ![]() $\langle Q\rangle$ is the expected value of
$\langle Q\rangle$ is the expected value of ![]() $Q$. From ergodic theory, the expected value can be estimated by spatial averaging over the two homogeneous directions, i.e.
$Q$. From ergodic theory, the expected value can be estimated by spatial averaging over the two homogeneous directions, i.e.
 \begin{equation} \langle Q\rangle (y,t) = \frac{1}{L_xL_z}\int_{-L_x/2}^{L_x/2}\int_{-L_z/2}^{L_z/2}Q(x,y,z,t) \,{\rm d}\kern0.7pt x\,{\rm d}z , \end{equation}
\begin{equation} \langle Q\rangle (y,t) = \frac{1}{L_xL_z}\int_{-L_x/2}^{L_x/2}\int_{-L_z/2}^{L_z/2}Q(x,y,z,t) \,{\rm d}\kern0.7pt x\,{\rm d}z , \end{equation}
and the Reynolds decomposition is used to define the fluctuating quantity ![]() $q(x,y,z,t) = Q(x,y,z,t) - \langle Q\rangle (y,t)$.
$q(x,y,z,t) = Q(x,y,z,t) - \langle Q\rangle (y,t)$.
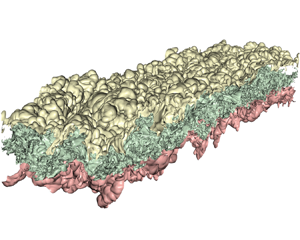
The computational domain used for the present study is displayed in figure 1, along with a snapshot of the passive scalar field at ![]() $t\,\Delta U/h_0=462$, where
$t\,\Delta U/h_0=462$, where ![]() $h_0$ refers to the initial visual thickness of the velocity field, defined by (4.1). The blue colour represents
$h_0$ refers to the initial visual thickness of the velocity field, defined by (4.1). The blue colour represents ![]() $\varPhi =1$, and the white represents
$\varPhi =1$, and the white represents ![]() $\varPhi =0$. Arrows represent the direction of the mean flow. The
$\varPhi =0$. Arrows represent the direction of the mean flow. The ![]() $x,y$ plane shown is extracted at
$x,y$ plane shown is extracted at ![]() $z=0$, with the positive
$z=0$, with the positive ![]() $z$ direction oriented out of the page.
$z$ direction oriented out of the page.

Figure 1. Simple two-dimensional schematic of the mixing layer configuration, showcasing a snapshot of the scalar field at ![]() $t\,\Delta U/h_0=462$, during the self-similar evolution. Dark blue represents
$t\,\Delta U/h_0=462$, during the self-similar evolution. Dark blue represents ![]() $\varPhi =1$, and white represents
$\varPhi =1$, and white represents ![]() $\varPhi =0$.
$\varPhi =0$.
To confirm that the grid spacing is adequately resolving the smallest scales of flow in the DNS, the ratio ![]() $\Delta x/\eta$ is computed and found to have a maximum value of
$\Delta x/\eta$ is computed and found to have a maximum value of ![]() $1.9$ during the transition to turbulence, with a value closer to
$1.9$ during the transition to turbulence, with a value closer to ![]() $1.3$ during the self-similar period of evolution. Here,
$1.3$ during the self-similar period of evolution. Here,
is the Kolmogorov scale, where the kinematic viscosity is ![]() $\upsilon =\mu /\rho$, the kinetic energy dissipation rate is
$\upsilon =\mu /\rho$, the kinetic energy dissipation rate is ![]() $\varepsilon =2\upsilon \left \langle s_{ij}s_{ij} \right \rangle$, and
$\varepsilon =2\upsilon \left \langle s_{ij}s_{ij} \right \rangle$, and ![]() $\eta$ is evaluated at the centreline of the mixing layer, corresponding to the maximum value of
$\eta$ is evaluated at the centreline of the mixing layer, corresponding to the maximum value of ![]() $\varepsilon$. According to Pope (Reference Pope2000),
$\varepsilon$. According to Pope (Reference Pope2000), ![]() $\Delta x/\eta \leq 2.1$ is required to resolve the smallest scales of motion, suggesting that the current simulation is resolving fluid motion on the dissipation scale of the flow.
$\Delta x/\eta \leq 2.1$ is required to resolve the smallest scales of motion, suggesting that the current simulation is resolving fluid motion on the dissipation scale of the flow.
3. Iso-surface equations
3.1. Standard iso-surface definitions
Consider a passive scalar field ![]() $\varPhi (x,y,z,t)$ that satisfies the advection–diffusion equation. An important related quantity is the diffusion velocity
$\varPhi (x,y,z,t)$ that satisfies the advection–diffusion equation. An important related quantity is the diffusion velocity ![]() $w_{dif}$, which is a measure of the propagation speed of an iso-surface relative to the fluid in the direction of the surface normal
$w_{dif}$, which is a measure of the propagation speed of an iso-surface relative to the fluid in the direction of the surface normal ![]() $n_i$ (Gibson Reference Gibson1968). For incompressible flow of a passive scalar field, the diffusion velocity is given by
$n_i$ (Gibson Reference Gibson1968). For incompressible flow of a passive scalar field, the diffusion velocity is given by
in the direction normal to the iso-surface
where
 \begin{equation} |\boldsymbol{\nabla} \varPhi| = \left(\frac{\partial \varPhi}{\partial x_i}\,\frac{\partial \varPhi}{\partial x_i}\right)^{1/2}, \end{equation}
\begin{equation} |\boldsymbol{\nabla} \varPhi| = \left(\frac{\partial \varPhi}{\partial x_i}\,\frac{\partial \varPhi}{\partial x_i}\right)^{1/2}, \end{equation}
and summation is implied on repeated indices. In addition to ![]() $n_i$ and
$n_i$ and ![]() $w_{dif}$, an iso-surface can be characterized by its surface curvature,
$w_{dif}$, an iso-surface can be characterized by its surface curvature,
where ![]() $k_1$ and
$k_1$ and ![]() $k_2$ are the principal curvatures of the iso-surface, and
$k_2$ are the principal curvatures of the iso-surface, and ![]() $\partial n_i/\partial x_i$ is equal to twice the mean curvature.
$\partial n_i/\partial x_i$ is equal to twice the mean curvature.
The area of an iso-surface is defined by Pope (Reference Pope1988) as
where ![]() $\mathcal {V}$ is an arbitrary volume, and
$\mathcal {V}$ is an arbitrary volume, and ![]() $\varSigma '$ is the iso-surface area density,
$\varSigma '$ is the iso-surface area density,
Here, ![]() $\varPhi _{iso}$ is the iso-value of
$\varPhi _{iso}$ is the iso-value of ![]() $\varPhi$ pertaining to the surface, and
$\varPhi$ pertaining to the surface, and ![]() $\delta ({\cdot })$ is the Dirac delta function (Vervisch et al. Reference Vervisch, Bidaux, Bray and Kollmann1995; Poinsot & Veynante Reference Poinsot and Veynante2005). The mean iso-surface area density
$\delta ({\cdot })$ is the Dirac delta function (Vervisch et al. Reference Vervisch, Bidaux, Bray and Kollmann1995; Poinsot & Veynante Reference Poinsot and Veynante2005). The mean iso-surface area density ![]() $\varSigma$ is defined as
$\varSigma$ is defined as
where ![]() $\left \langle {\cdot } \right \rangle$ denotes the expected value.
$\left \langle {\cdot } \right \rangle$ denotes the expected value.
Based on (3.7), a transport equation for the mean surface area density ![]() $\varSigma$ can be derived (Trouvé & Poinsot Reference Trouvé and Poinsot1994; van Kalmthout & Veynante Reference van Kalmthout and Veynante1998):
$\varSigma$ can be derived (Trouvé & Poinsot Reference Trouvé and Poinsot1994; van Kalmthout & Veynante Reference van Kalmthout and Veynante1998):
 \begin{align} \frac{\partial \varSigma}{\partial t} = \underbrace{-\frac{\partial }{\partial x_i}\left(\left\langle U_i \right\rangle_s\varSigma\right)}_{\mathcal{T}_U} + \underbrace{\left\langle \frac{\partial U_i}{\partial x_i} - n_in_j\,\frac{\partial U_i}{\partial x_j} \right\rangle_s\varSigma}_{\mathcal{P}} \underbrace{{}-\frac{\partial }{\partial x_i}\left(\left\langle w_{dif} n_i \right\rangle_s\varSigma\right)}_{\mathcal{T}_D} + \underbrace{\left\langle w_{dif}\,\frac{\partial n_i}{\partial x_i} \right\rangle_s\varSigma}_{-\mathcal{D}}. \end{align}
\begin{align} \frac{\partial \varSigma}{\partial t} = \underbrace{-\frac{\partial }{\partial x_i}\left(\left\langle U_i \right\rangle_s\varSigma\right)}_{\mathcal{T}_U} + \underbrace{\left\langle \frac{\partial U_i}{\partial x_i} - n_in_j\,\frac{\partial U_i}{\partial x_j} \right\rangle_s\varSigma}_{\mathcal{P}} \underbrace{{}-\frac{\partial }{\partial x_i}\left(\left\langle w_{dif} n_i \right\rangle_s\varSigma\right)}_{\mathcal{T}_D} + \underbrace{\left\langle w_{dif}\,\frac{\partial n_i}{\partial x_i} \right\rangle_s\varSigma}_{-\mathcal{D}}. \end{align}
The operator ![]() $\left \langle {\cdot } \right \rangle _s$ refers to a surface average, defined for an arbitrary property
$\left \langle {\cdot } \right \rangle _s$ refers to a surface average, defined for an arbitrary property ![]() $Q$ by
$Q$ by
For convenience, the destruction term ![]() ${\mathcal {D}}$ has been defined with a leading negative sign due to the term taking on a negative value almost exclusively in the present data. From this definition, the equation for the iso-surface area density can be written simply as
${\mathcal {D}}$ has been defined with a leading negative sign due to the term taking on a negative value almost exclusively in the present data. From this definition, the equation for the iso-surface area density can be written simply as ![]() $\partial \varSigma /\partial t=\mathcal {T}_U + \mathcal {P} + \mathcal {T_D} - \mathcal {D}$. The terms in (3.8) refer to, in order, the rate of change of the mean iso-surface area density,
$\partial \varSigma /\partial t=\mathcal {T}_U + \mathcal {P} + \mathcal {T_D} - \mathcal {D}$. The terms in (3.8) refer to, in order, the rate of change of the mean iso-surface area density, ![]() $\partial \varSigma /\partial t$, the transport of
$\partial \varSigma /\partial t$, the transport of ![]() $\varSigma$ due to the velocity field,
$\varSigma$ due to the velocity field, ![]() $\mathcal {T}_U$, the rate of production of
$\mathcal {T}_U$, the rate of production of ![]() $\varSigma$ due to the flow strain rate,
$\varSigma$ due to the flow strain rate, ![]() $\mathcal {P}$, the transport of
$\mathcal {P}$, the transport of ![]() $\varSigma$ due to molecular diffusion,
$\varSigma$ due to molecular diffusion, ![]() $\mathcal {T}_D$, and the rate of destruction of
$\mathcal {T}_D$, and the rate of destruction of ![]() $\varSigma$ due to the combined effects of molecular diffusion and surface curvature,
$\varSigma$ due to the combined effects of molecular diffusion and surface curvature, ![]() $\mathcal {D}$. Note that although the current formulation assumes a passive scalar field that propagates via molecular diffusion, the effects of an active scalar field, such as a premixed flame surface, can be accounted for by including the effects of chemical reactions on the diffusion velocity in (3.1).
$\mathcal {D}$. Note that although the current formulation assumes a passive scalar field that propagates via molecular diffusion, the effects of an active scalar field, such as a premixed flame surface, can be accounted for by including the effects of chemical reactions on the diffusion velocity in (3.1).
3.2. Iso-surface averaging in a mixing layer
Evaluating surface-weighted averages, especially for highly contorted surfaces such as those present in turbulent flows, is a challenging and nuanced problem. This study utilizes the same methodology described in the previous paper (Blakeley et al. Reference Blakeley, Olson and Riley2022, Appendix A) to evaluate iso-surface integrals, which is based on the work by Storti (Reference Storti2010) and Yurtoglu, Carton & Storti (Reference Yurtoglu, Carton and Storti2018). In essence, the approach yields a mathematically consistent approximation for ![]() $\varSigma '$, given in (3.6), for a discrete, implicitly defined scalar field on a uniform three-dimensional grid. The resulting field is a function of three-dimensional spatial coordinates
$\varSigma '$, given in (3.6), for a discrete, implicitly defined scalar field on a uniform three-dimensional grid. The resulting field is a function of three-dimensional spatial coordinates ![]() $x$,
$x$, ![]() $y$,
$y$, ![]() $z$, and time
$z$, and time ![]() $t$, and depends on the chosen iso-value
$t$, and depends on the chosen iso-value ![]() $\varPhi _{iso}$. Note that
$\varPhi _{iso}$. Note that ![]() $\varSigma '(x,y,z,t;\varPhi _{iso})$ contains mostly zero values; the function is non-zero only in the grid cells immediately adjacent to the iso-surface.
$\varSigma '(x,y,z,t;\varPhi _{iso})$ contains mostly zero values; the function is non-zero only in the grid cells immediately adjacent to the iso-surface.
Using statistical homogeneity in the ![]() $x$ and
$x$ and ![]() $z$ directions, and ergodic theory, the mean surface area density
$z$ directions, and ergodic theory, the mean surface area density ![]() $\varSigma$ is given by
$\varSigma$ is given by
 \begin{equation} \varSigma(y,t) = \frac{1}{L_xL_z (m\,\Delta y)}\int_{-L_x/2}^{L_x/2}\int_{y}^{y+(m\,\Delta y)}\int_{-L_z/2}^{L_z/2}\varSigma'(x,y,z,t)\,{\rm d}\kern0.7pt x\,{\rm d}y\,{\rm d}z, \end{equation}
\begin{equation} \varSigma(y,t) = \frac{1}{L_xL_z (m\,\Delta y)}\int_{-L_x/2}^{L_x/2}\int_{y}^{y+(m\,\Delta y)}\int_{-L_z/2}^{L_z/2}\varSigma'(x,y,z,t)\,{\rm d}\kern0.7pt x\,{\rm d}y\,{\rm d}z, \end{equation}
where ![]() $m$ is an integer value that denotes the number of grid points included in the average in the
$m$ is an integer value that denotes the number of grid points included in the average in the ![]() $y$ direction. For
$y$ direction. For ![]() $m=1$, this average reduces to the two-dimensional average defined in (2.1). In the present study, a value
$m=1$, this average reduces to the two-dimensional average defined in (2.1). In the present study, a value ![]() $m=16$ is used to reduce statistical fluctuations in the resulting
$m=16$ is used to reduce statistical fluctuations in the resulting ![]() $y$ profiles. From a physical standpoint, the mean iso-surface area density
$y$ profiles. From a physical standpoint, the mean iso-surface area density ![]() $\varSigma (y,t)$ can be interpreted as the average iso-surface area per unit volume contained in a slab of size
$\varSigma (y,t)$ can be interpreted as the average iso-surface area per unit volume contained in a slab of size ![]() $L_xL_z(m\,\Delta y)$, which is a function of the both the cross-stream direction
$L_xL_z(m\,\Delta y)$, which is a function of the both the cross-stream direction ![]() $y$ and time
$y$ and time ![]() $t$, and has units of
$t$, and has units of ![]() $1/\text {length}$. The
$1/\text {length}$. The ![]() $y$ profiles of
$y$ profiles of ![]() $\varSigma$ were compared for values of
$\varSigma$ were compared for values of ![]() $m$ ranging from
$m$ ranging from ![]() $1$ to
$1$ to ![]() $20$, and were found to be insensitive to the value of
$20$, and were found to be insensitive to the value of ![]() $m$ as long as
$m$ as long as ![]() $(m\,\Delta y)$ is small compared to the length scale of the mean flow.
$(m\,\Delta y)$ is small compared to the length scale of the mean flow.
Although the iso-surface average defined in (3.9) is utilized often in the literature, it can be poorly defined unless integrated over the entire iso-surface. In the case of the present DNS, it was found that the iso-surface area density ![]() $\varSigma (y,t)$ takes on a Gaussian-like profile that decays to zero away from its peak (refer to § 4). This means that, as given by (3.9), the iso-surface average
$\varSigma (y,t)$ takes on a Gaussian-like profile that decays to zero away from its peak (refer to § 4). This means that, as given by (3.9), the iso-surface average ![]() $\langle Q\rangle _s$ is undefined near the edges of the mixing layer because
$\langle Q\rangle _s$ is undefined near the edges of the mixing layer because ![]() $\varSigma \rightarrow 0$ as
$\varSigma \rightarrow 0$ as ![]() $y\rightarrow \pm L_y/2$. While the surface average is an intuitive concept, it is more practical to consider instead the weighted surface average
$y\rightarrow \pm L_y/2$. While the surface average is an intuitive concept, it is more practical to consider instead the weighted surface average
 \begin{equation} \langle Q\rangle _s\varSigma = \left\langle Q\varSigma ' \right\rangle = \frac{1}{L_xL_z(m\,\Delta y)}\int_{-L_x/2}^{L_x/2}\int_{y}^{y+(m\,\Delta y)}\int_{-L_z/2}^{L_z/2}Q\varSigma'\,{\rm d}\kern0.7pt x\,{\rm d}y\,{\rm d}z. \end{equation}
\begin{equation} \langle Q\rangle _s\varSigma = \left\langle Q\varSigma ' \right\rangle = \frac{1}{L_xL_z(m\,\Delta y)}\int_{-L_x/2}^{L_x/2}\int_{y}^{y+(m\,\Delta y)}\int_{-L_z/2}^{L_z/2}Q\varSigma'\,{\rm d}\kern0.7pt x\,{\rm d}y\,{\rm d}z. \end{equation}
In fact, from inspection of (3.8), it can be seen that each of the terms on the right-hand side of the equation makes use of the weighted iso-surface average ![]() $\left \langle Q\varSigma ' \right \rangle$, rather than the iso-surface average
$\left \langle Q\varSigma ' \right \rangle$, rather than the iso-surface average ![]() $\langle Q\rangle _s$. As discussed above, the value of
$\langle Q\rangle _s$. As discussed above, the value of ![]() $m$ in the present study is set to
$m$ in the present study is set to ![]() $16$, which provides good statistical convergence. In addition, the data have been averaged in time to reduce statistical fluctuations, with averaging width approximately
$16$, which provides good statistical convergence. In addition, the data have been averaged in time to reduce statistical fluctuations, with averaging width approximately ![]() $8$ non-dimensional time units,
$8$ non-dimensional time units, ![]() $t\,\Delta U/h_0$. As will be shown below, the terms in (3.8) are expected to vary smoothly in time and space such that the averaging process described accurately retains the characteristic features of the flow.
$t\,\Delta U/h_0$. As will be shown below, the terms in (3.8) are expected to vary smoothly in time and space such that the averaging process described accurately retains the characteristic features of the flow.
In some cases, it is helpful to understand a quantity that has been averaged over the entire iso-surface contained in the computational domain. In these cases, the quantity can be evaluated by integrating the averaged quantity in the cross-stream direction. For example, the surface area of an iso-surface, ![]() $A_{iso}$, can be evaluated by
$A_{iso}$, can be evaluated by
 \begin{equation} \frac{A_{iso}}{A_0} = \int_{-L_y/2}^{L_y/2}\varSigma\,{{\rm d}y}, \end{equation}
\begin{equation} \frac{A_{iso}}{A_0} = \int_{-L_y/2}^{L_y/2}\varSigma\,{{\rm d}y}, \end{equation}
where ![]() $A_0=L_xL_z$ is the surface area at
$A_0=L_xL_z$ is the surface area at ![]() $t=0$.
$t=0$.
4. Self-similar development of the temporal mixing layer
It is well known that the velocity field in a temporal mixing layer attains a period of self-similar development, in which the mixed region of fluid grows outward from the centreline at a constant rate, i.e. ![]() ${\rm d}\delta _m/{\rm d}t=\mathrm {const.}$ (Rogers & Moser Reference Rogers and Moser1994). Another way to measure the width of the mixed region of fluid is the ‘visual’ thickness (Rogers & Moser Reference Rogers and Moser1994),
${\rm d}\delta _m/{\rm d}t=\mathrm {const.}$ (Rogers & Moser Reference Rogers and Moser1994). Another way to measure the width of the mixed region of fluid is the ‘visual’ thickness (Rogers & Moser Reference Rogers and Moser1994),
which is a measure of distance in the ![]() $y$ direction between the top and bottom 10 % of the mean velocity profile
$y$ direction between the top and bottom 10 % of the mean velocity profile ![]() $\left \langle U \right \rangle$, as used in the recent study by Baltzer & Livescu (Reference Baltzer and Livescu2020). In addition to the velocity field, it can be shown that a passive scalar field will also develop in a self-similar manner. Analogously, a scalar visual thickness
$\left \langle U \right \rangle$, as used in the recent study by Baltzer & Livescu (Reference Baltzer and Livescu2020). In addition to the velocity field, it can be shown that a passive scalar field will also develop in a self-similar manner. Analogously, a scalar visual thickness ![]() $h_\varPhi$ can be defined as
$h_\varPhi$ can be defined as
As with the visual thickness of the velocity field, the scalar visual thickness is a measure of the spatial extent of ![]() $\left \langle \varPhi \right \rangle$ in the
$\left \langle \varPhi \right \rangle$ in the ![]() $y$ direction. An important consequence of self-similarity is that the above length scales, measuring the width of the mixing layer, are proportional to each other and increase at a constant rate (though the constant coefficient of increase may differ). For the present DNS, the value of the growth rate of the momentum thickness
$y$ direction. An important consequence of self-similarity is that the above length scales, measuring the width of the mixing layer, are proportional to each other and increase at a constant rate (though the constant coefficient of increase may differ). For the present DNS, the value of the growth rate of the momentum thickness ![]() $\delta _m$ is approximately
$\delta _m$ is approximately ![]() $0.014$ during the self-similar period, which is consistent with previous mixing layer experiments and simulations (Bell & Mehta Reference Bell and Mehta1990; Rogers & Moser Reference Rogers and Moser1994; Almagro, García-Villalba & Flores Reference Almagro, García-Villalba and Flores2017; Baltzer & Livescu Reference Baltzer and Livescu2020).
$0.014$ during the self-similar period, which is consistent with previous mixing layer experiments and simulations (Bell & Mehta Reference Bell and Mehta1990; Rogers & Moser Reference Rogers and Moser1994; Almagro, García-Villalba & Flores Reference Almagro, García-Villalba and Flores2017; Baltzer & Livescu Reference Baltzer and Livescu2020).
To verify the self-similar behaviour of the shear layer, scaled profiles of several important quantities, namely the streamwise velocity fluctuations ![]() $u^2$, the dissipation rate of turbulent kinetic energy
$u^2$, the dissipation rate of turbulent kinetic energy ![]() $\varepsilon$, the scalar variance
$\varepsilon$, the scalar variance ![]() $\phi ^2$, and the dissipation rate of scalar variance
$\phi ^2$, and the dissipation rate of scalar variance ![]() $\chi$, are shown in figure 2. It can be observed that the scaled instantaneous profiles (dashed, coloured lines) of these averages collapse nicely onto a single curve (given by the solid black line) when scaled appropriately. Based on these data, the following self-similar forms are found to be
$\chi$, are shown in figure 2. It can be observed that the scaled instantaneous profiles (dashed, coloured lines) of these averages collapse nicely onto a single curve (given by the solid black line) when scaled appropriately. Based on these data, the following self-similar forms are found to be
and
where the similarity variable is ![]() $\xi =y/h(t)$. These self-similar forms are consistent with previous studies that have examined the mixing layer (Rogers & Moser Reference Rogers and Moser1994; Almagro et al. Reference Almagro, García-Villalba and Flores2017; Baltzer & Livescu Reference Baltzer and Livescu2020), which lends confidence to the present results and demonstrates that the present simulation of a temporal mixing layer enters a robust period of self-similarity between the non-dimensional times approximately
$\xi =y/h(t)$. These self-similar forms are consistent with previous studies that have examined the mixing layer (Rogers & Moser Reference Rogers and Moser1994; Almagro et al. Reference Almagro, García-Villalba and Flores2017; Baltzer & Livescu Reference Baltzer and Livescu2020), which lends confidence to the present results and demonstrates that the present simulation of a temporal mixing layer enters a robust period of self-similarity between the non-dimensional times approximately ![]() $250$ and
$250$ and ![]() $580$.
$580$.

Figure 2. Self-similar profiles of (a) streamwise velocity fluctuations ![]() $u^2$, (b) dissipation rate of turbulent kinetic energy
$u^2$, (b) dissipation rate of turbulent kinetic energy ![]() $\varepsilon$, (c) scalar variance
$\varepsilon$, (c) scalar variance ![]() $\phi ^2$ and (d) dissipation rate of scalar variance
$\phi ^2$ and (d) dissipation rate of scalar variance ![]() $\chi$. Dashed coloured lines indicate instantaneous scaled profiles, and the solid black curve indicates the time average over the self-similar period.
$\chi$. Dashed coloured lines indicate instantaneous scaled profiles, and the solid black curve indicates the time average over the self-similar period.
During this period, ![]() $h/h_0$ goes from a value of approximately
$h/h_0$ goes from a value of approximately ![]() $22$ to
$22$ to ![]() $41$, an increase of
$41$, an increase of ![]() $86\,\%$. A large increase in
$86\,\%$. A large increase in ![]() $h$ is desired in order to evaluate the self-similarity of quantities in the flow; if the change in
$h$ is desired in order to evaluate the self-similarity of quantities in the flow; if the change in ![]() $h$ is small compared to statistical fluctuations, it can become difficult to differentiate statistical variation from true time-dependent behaviour. Even in the present DNS, subtle distinctions can be difficult to quantify due to the effects of the finite Reynolds number. In particular, despite the significant increase in
$h$ is small compared to statistical fluctuations, it can become difficult to differentiate statistical variation from true time-dependent behaviour. Even in the present DNS, subtle distinctions can be difficult to quantify due to the effects of the finite Reynolds number. In particular, despite the significant increase in ![]() $h$, the Taylor length scale and Kolmogorov microscale exhibit only modest increases of
$h$, the Taylor length scale and Kolmogorov microscale exhibit only modest increases of ![]() $35\,\%$ and
$35\,\%$ and ![]() $19\,\%$, respectively, during the self-similar period. The relatively small difference between the two length scales makes it difficult (though not impossible) to distinguish between the two. Here, the Taylor length scale is defined as (Pope Reference Pope2000)
$19\,\%$, respectively, during the self-similar period. The relatively small difference between the two length scales makes it difficult (though not impossible) to distinguish between the two. Here, the Taylor length scale is defined as (Pope Reference Pope2000)
 \begin{equation} \lambda_g = \left(\frac{15\upsilon}{\varepsilon}\right)^{1/2}u_{rms}, \end{equation}
\begin{equation} \lambda_g = \left(\frac{15\upsilon}{\varepsilon}\right)^{1/2}u_{rms}, \end{equation}
where ![]() $u_{rms}=\left \langle (u^2+v^2+w^2)/3 \right \rangle ^{1/2}$. For the results presented here, the scalar Taylor length scale
$u_{rms}=\left \langle (u^2+v^2+w^2)/3 \right \rangle ^{1/2}$. For the results presented here, the scalar Taylor length scale ![]() $\lambda _\phi$, defined as (Donzis, Sreenivasan & Yeung Reference Donzis, Sreenivasan and Yeung2005)
$\lambda _\phi$, defined as (Donzis, Sreenivasan & Yeung Reference Donzis, Sreenivasan and Yeung2005)
will be used, because the Taylor scales are proportional to each other (i.e. ![]() $\lambda _g\propto \lambda _\phi$ for
$\lambda _g\propto \lambda _\phi$ for ![]() $Sc\approx 1$). The corresponding increases of the turbulent Reynolds number
$Sc\approx 1$). The corresponding increases of the turbulent Reynolds number ![]() ${Re} = u_{rms} h/\upsilon$ and the Taylor Reynolds number
${Re} = u_{rms} h/\upsilon$ and the Taylor Reynolds number ![]() ${Re}_\lambda = u_{rms} \lambda _g/\upsilon$ over the self-similar period are from 12 000 to 22 000, and from 115 to 135, respectively.
${Re}_\lambda = u_{rms} \lambda _g/\upsilon$ over the self-similar period are from 12 000 to 22 000, and from 115 to 135, respectively.
To give additional context in the following sections, two results from Blakeley et al. (Reference Blakeley, Olson and Riley2022) will be summarized here. First, the temporal evolution of the iso-surface area in the present shear layer, for values of ![]() $\varPhi _{iso}$ corresponding to
$\varPhi _{iso}$ corresponding to ![]() $\varPhi _{iso} = 0.05,0.25,0.5,0.75,0.95$, is shown in figure 3(a). The surface area is found to increase steeply during the transition to turbulence, but then continue to increase at a moderate rate throughout the self-similar period of the mixing layer development, for all values of
$\varPhi _{iso} = 0.05,0.25,0.5,0.75,0.95$, is shown in figure 3(a). The surface area is found to increase steeply during the transition to turbulence, but then continue to increase at a moderate rate throughout the self-similar period of the mixing layer development, for all values of ![]() $\varPhi _{iso}$.
$\varPhi _{iso}$.

Figure 3. (a) Temporal evolution of iso-surface area ![]() $A_{iso}$, for
$A_{iso}$, for ![]() $\varPhi _{iso}=0.05,0.25,0.5,0.75,0.95$. Self-similar, cross-stream profiles of iso-surface area density
$\varPhi _{iso}=0.05,0.25,0.5,0.75,0.95$. Self-similar, cross-stream profiles of iso-surface area density ![]() $\varSigma$, for (b)
$\varSigma$, for (b) ![]() $\varPhi _{iso}=0.5$ and (c)
$\varPhi _{iso}=0.5$ and (c) ![]() $\varPhi _{iso}=0.95$. Dashed lines are instantaneous profiles of
$\varPhi _{iso}=0.95$. Dashed lines are instantaneous profiles of ![]() $\varSigma \lambda _\phi$, and the solid black curve represents the time average over the self-similar period
$\varSigma \lambda _\phi$, and the solid black curve represents the time average over the self-similar period ![]() $250\leq t\,\Delta U/h_0 \leq 580$.
$250\leq t\,\Delta U/h_0 \leq 580$.
Second, this continued increase in ![]() $A_{iso}$ can be understood better by examining the cross-stream profiles of the surface area density
$A_{iso}$ can be understood better by examining the cross-stream profiles of the surface area density ![]() $\varSigma$, which are shown to evolve in a self-similar manner when plotted against the similarity variable
$\varSigma$, which are shown to evolve in a self-similar manner when plotted against the similarity variable ![]() $\xi =y/h$, and normalized by the scalar Taylor length scale
$\xi =y/h$, and normalized by the scalar Taylor length scale ![]() $\lambda _\phi$. Instantaneous profiles of
$\lambda _\phi$. Instantaneous profiles of ![]() $\varSigma$, normalized by
$\varSigma$, normalized by ![]() $\lambda _\phi$, are plotted in figures 3(b,c) as dashed lines, for iso-surfaces
$\lambda _\phi$, are plotted in figures 3(b,c) as dashed lines, for iso-surfaces ![]() $\varPhi _{iso}=0.5$ and
$\varPhi _{iso}=0.5$ and ![]() $0.95$, respectively. The solid black line represents the time average of the instantaneous curves over the self-similar period, which was determined empirically to begin at approximately
$0.95$, respectively. The solid black line represents the time average of the instantaneous curves over the self-similar period, which was determined empirically to begin at approximately ![]() $t\,\Delta U/h_0=250$. These data demonstrate that despite the peak value of
$t\,\Delta U/h_0=250$. These data demonstrate that despite the peak value of ![]() $\varSigma$ decreasing in time proportional to
$\varSigma$ decreasing in time proportional to ![]() $\lambda _\phi$, the width of
$\lambda _\phi$, the width of ![]() $\varSigma$ increases with the mixing layer width
$\varSigma$ increases with the mixing layer width ![]() $h$, resulting in a net increase of iso-surface area over the self-similar period. For more details regarding the present DNS, interested readers are referred to Blakeley et al. (Reference Blakeley, Olson and Riley2022).
$h$, resulting in a net increase of iso-surface area over the self-similar period. For more details regarding the present DNS, interested readers are referred to Blakeley et al. (Reference Blakeley, Olson and Riley2022).
Note that due to the problem configuration, the behaviour of iso-surfaces is symmetric about ![]() $\varPhi _{iso}=0.5$, i.e. the statistics of the iso-surface
$\varPhi _{iso}=0.5$, i.e. the statistics of the iso-surface ![]() $\varPhi = \varPhi _{iso}$ are expected to match the statistics of the iso-surface corresponding to
$\varPhi = \varPhi _{iso}$ are expected to match the statistics of the iso-surface corresponding to ![]() $\varPhi = |1-\varPhi _{iso}|$ (see e.g. the curves for
$\varPhi = |1-\varPhi _{iso}|$ (see e.g. the curves for ![]() $\varPhi _{iso} = 0.25$ and
$\varPhi _{iso} = 0.25$ and ![]() $0.75$ in figure 3a). Because of this symmetry, the results presented below will contain results from
$0.75$ in figure 3a). Because of this symmetry, the results presented below will contain results from ![]() $\varPhi _{iso}\geq 0.5$, with the understanding that equivalent behaviour is observed in iso-surfaces corresponding to
$\varPhi _{iso}\geq 0.5$, with the understanding that equivalent behaviour is observed in iso-surfaces corresponding to ![]() $\varPhi _{iso}<0.5$. Furthermore, discrepancies between symmetric iso-surfaces can give some estimate of the error in the simulation, especially when considering that symmetric iso-surfaces are interacting with turbulent motions on opposing sides of the computational domain and therefore have a measure of statistical independence.
$\varPhi _{iso}<0.5$. Furthermore, discrepancies between symmetric iso-surfaces can give some estimate of the error in the simulation, especially when considering that symmetric iso-surfaces are interacting with turbulent motions on opposing sides of the computational domain and therefore have a measure of statistical independence.
5. Behaviour of the terms in the iso-surface area density transport equation
In this section, the evolution of iso-surface area ![]() $A_{iso}$ and iso-surface area density
$A_{iso}$ and iso-surface area density ![]() $\varSigma$ will be examined. In particular, it will be demonstrated that direct measurements of
$\varSigma$ will be examined. In particular, it will be demonstrated that direct measurements of ![]() ${\rm d}A_{iso}/{\rm d}t$ and
${\rm d}A_{iso}/{\rm d}t$ and ![]() $\partial \varSigma /\partial t$ are in quantitative agreement with the rates of change implied from the transport equations. This serves as a check of the numerical methods, as well as a starting point for future explorations into the data.
$\partial \varSigma /\partial t$ are in quantitative agreement with the rates of change implied from the transport equations. This serves as a check of the numerical methods, as well as a starting point for future explorations into the data.
5.1. Iso-surface area
Consider the integral of (3.8) over the cross-stream direction,
 \begin{equation} \frac{\mathrm{d}}{\mathrm{d}t}\int_{-Ly/2}^{Ly/2}\varSigma\,\mathrm{d} y =- \int_{-Ly/2}^{Ly/2}\left\langle n_in_jS_{ij} \right\rangle_s\varSigma\,\mathrm{d} y + \int_{-Ly/2}^{Ly/2}\left\langle w_{dif}\,\frac{\partial n_i}{\partial x_i} \right\rangle_s\varSigma\,\mathrm{d}y, \end{equation}
\begin{equation} \frac{\mathrm{d}}{\mathrm{d}t}\int_{-Ly/2}^{Ly/2}\varSigma\,\mathrm{d} y =- \int_{-Ly/2}^{Ly/2}\left\langle n_in_jS_{ij} \right\rangle_s\varSigma\,\mathrm{d} y + \int_{-Ly/2}^{Ly/2}\left\langle w_{dif}\,\frac{\partial n_i}{\partial x_i} \right\rangle_s\varSigma\,\mathrm{d}y, \end{equation}
where the advective and diffusive transport terms are identically zero due to the zero flux boundary conditions, the production term has been simplified for constant density flow, and the time derivative has been moved outside the integral, assuming that the time derivative and the integration in ![]() $y$ commute. From (3.12) it can be shown that by integrating over the entire domain in
$y$ commute. From (3.12) it can be shown that by integrating over the entire domain in ![]() $y$, the above equation describes the rate of change of iso-surface area
$y$, the above equation describes the rate of change of iso-surface area ![]() ${\rm d}A_{iso}/{\rm d}t$, normalized by the surface area of a plane in the
${\rm d}A_{iso}/{\rm d}t$, normalized by the surface area of a plane in the ![]() $x,z$ directions,
$x,z$ directions, ![]() $A_0=L_xL_z$. According to (5.1), the rate of change of iso-surface area is determined by the difference between the integrated production term
$A_0=L_xL_z$. According to (5.1), the rate of change of iso-surface area is determined by the difference between the integrated production term ![]() $\int \mathcal {P}$ and the integrated destruction term
$\int \mathcal {P}$ and the integrated destruction term ![]() $\int \mathcal {D}$, i.e.
$\int \mathcal {D}$, i.e. ![]() ${\rm d}A_{iso}/{\rm d}t = A_0(\int \mathcal {P} - \int \mathcal {D})$ (Wang Reference Wang2013).
${\rm d}A_{iso}/{\rm d}t = A_0(\int \mathcal {P} - \int \mathcal {D})$ (Wang Reference Wang2013).
The temporal evolutions of ![]() ${\rm d}A_{iso}/{\rm d}t$,
${\rm d}A_{iso}/{\rm d}t$, ![]() $\int \mathcal {P}$ and
$\int \mathcal {P}$ and ![]() $\int \mathcal {D}$ in (5.1) are plotted in figures 4(a,b) for
$\int \mathcal {D}$ in (5.1) are plotted in figures 4(a,b) for ![]() $\varPhi _{iso}=0.5$ and
$\varPhi _{iso}=0.5$ and ![]() $0.95$, respectively. An explicit finite difference approximation is used to estimate
$0.95$, respectively. An explicit finite difference approximation is used to estimate ![]() ${\rm d}A_{iso}/{\rm d}t$ from the DNS data. Note that this is a somewhat inaccurate approximation, as these quantities were calculated during post-processing using restart files that were saved once every 200 physical time steps, which degrades the temporal accuracy of the finite difference approximation. The lack of temporal resolution is evidenced clearly by the discrepancy between the direct approximation of
${\rm d}A_{iso}/{\rm d}t$ from the DNS data. Note that this is a somewhat inaccurate approximation, as these quantities were calculated during post-processing using restart files that were saved once every 200 physical time steps, which degrades the temporal accuracy of the finite difference approximation. The lack of temporal resolution is evidenced clearly by the discrepancy between the direct approximation of ![]() ${\rm d}A_{iso}/{\rm d}t$ (dotted line) with the rate of change implied from the right-hand side of (5.1) (blue circles), especially early in the simulation,
${\rm d}A_{iso}/{\rm d}t$ (dotted line) with the rate of change implied from the right-hand side of (5.1) (blue circles), especially early in the simulation, ![]() $t\,\Delta U/h_0 < 200$. Nonetheless, in the self-similar region,
$t\,\Delta U/h_0 < 200$. Nonetheless, in the self-similar region, ![]() $t\,\Delta U/h_0>250$, the left-hand and right-hand sides of (5.1) are in approximate balance.
$t\,\Delta U/h_0>250$, the left-hand and right-hand sides of (5.1) are in approximate balance.

Figure 4. Temporal evolution of terms in the iso-surface area transport equation (5.1), for (a) ![]() $\varPhi _{iso} = 0.5$ and (b)
$\varPhi _{iso} = 0.5$ and (b) ![]() $\varPhi _{iso} = 0.95$, non-dimensionalized by
$\varPhi _{iso} = 0.95$, non-dimensionalized by ![]() $h_0/\Delta U$. Blue circles indicate
$h_0/\Delta U$. Blue circles indicate ![]() ${\rm d}A_{iso}/{\rm d}t$, green up-triangles indicate
${\rm d}A_{iso}/{\rm d}t$, green up-triangles indicate ![]() $\int \mathcal {P}$, purple down-triangles indicate
$\int \mathcal {P}$, purple down-triangles indicate ![]() $\int \mathcal {D}$ and
$\int \mathcal {D}$ and ![]() $\int \mathcal {P} - \int \mathcal {D}$ is given by a dotted line. Additionally, the non-dimensional, integrated dissipation rates of kinetic energy and scalar variance,
$\int \mathcal {P} - \int \mathcal {D}$ is given by a dotted line. Additionally, the non-dimensional, integrated dissipation rates of kinetic energy and scalar variance, ![]() $\mathcal {E}/\Delta U^3$ and
$\mathcal {E}/\Delta U^3$ and ![]() $\mathcal {X}/(\Delta U\,\Delta \varPhi ^2)$, have been scaled by constant values and are plotted as dashed and dash-dotted lines, respectively. Note the difference in scales between (a) and (b).
$\mathcal {X}/(\Delta U\,\Delta \varPhi ^2)$, have been scaled by constant values and are plotted as dashed and dash-dotted lines, respectively. Note the difference in scales between (a) and (b).
The steep growth of ![]() $A_{iso}$ during the transition to turbulence can be identified in figure 4 as a small peak in the evolution of
$A_{iso}$ during the transition to turbulence can be identified in figure 4 as a small peak in the evolution of ![]() ${\rm d}A_{iso}/{\rm d}t$, but more clearly as a steep increase in the magnitude of both terms
${\rm d}A_{iso}/{\rm d}t$, but more clearly as a steep increase in the magnitude of both terms ![]() $\int \mathcal {P}$ and
$\int \mathcal {P}$ and ![]() $\int \mathcal {D}$ around
$\int \mathcal {D}$ around ![]() $t\,\Delta U/h_0\approx 100$. In this transitional period, the magnitude of term
$t\,\Delta U/h_0\approx 100$. In this transitional period, the magnitude of term ![]() $\int \mathcal {D}$ lags slightly behind term
$\int \mathcal {D}$ lags slightly behind term ![]() $\int \mathcal {P}$, resulting in the initial growth of surface area.
$\int \mathcal {P}$, resulting in the initial growth of surface area.
Notably, the evolutions of terms ![]() $\int \mathcal {P}$ and
$\int \mathcal {P}$ and ![]() $\int \mathcal {D}$ are approximately proportional to the integrated dissipation rates of turbulent kinetic energy and scalar variance, defined as
$\int \mathcal {D}$ are approximately proportional to the integrated dissipation rates of turbulent kinetic energy and scalar variance, defined as
 \begin{equation} \mathcal{E} = \int^{L_y/2}_{-L_y/2}\varepsilon\,{{\rm d} y} \end{equation}
\begin{equation} \mathcal{E} = \int^{L_y/2}_{-L_y/2}\varepsilon\,{{\rm d} y} \end{equation}and
 \begin{equation} \mathcal{X} = \int^{L_y/2}_{-L_y/2}\chi\,{{\rm d}y}, \end{equation}
\begin{equation} \mathcal{X} = \int^{L_y/2}_{-L_y/2}\chi\,{{\rm d}y}, \end{equation}
respectively (Rogers & Moser Reference Rogers and Moser1994; Baltzer & Livescu Reference Baltzer and Livescu2020).The integrated dissipation rates ![]() $\mathcal {E}$ and
$\mathcal {E}$ and ![]() $\mathcal {X}$, multiplied by constants
$\mathcal {X}$, multiplied by constants ![]() $c_1$ and
$c_1$ and ![]() $-c_2$, respectively, are displayed in figure 4 as dashed and dash-dotted lines. The constant values are chosen empirically to highlight the similarity between the temporal evolution of the integrated dissipation rates and the integrated rates of production and destruction of iso-surface area. The values of
$-c_2$, respectively, are displayed in figure 4 as dashed and dash-dotted lines. The constant values are chosen empirically to highlight the similarity between the temporal evolution of the integrated dissipation rates and the integrated rates of production and destruction of iso-surface area. The values of ![]() $c_1$ and
$c_1$ and ![]() $c_2$ are constant in time but range from
$c_2$ are constant in time but range from ![]() ${\approx } 5$ to
${\approx } 5$ to ![]() $150$, depending on the value of
$150$, depending on the value of ![]() $\varPhi _{iso}$.
$\varPhi _{iso}$.
The similarity between ![]() $\int \mathcal {P}$ and
$\int \mathcal {P}$ and ![]() $\mathcal {E}$ is expected from previous models of flame surface area, which typically assume that
$\mathcal {E}$ is expected from previous models of flame surface area, which typically assume that ![]() $\int \mathcal {P}\sim (\varepsilon /\upsilon )^{1/2}$ or
$\int \mathcal {P}\sim (\varepsilon /\upsilon )^{1/2}$ or ![]() $\int \mathcal {P}\sim \varepsilon /k$ (see Poinsot & Veynante (Reference Poinsot and Veynante2005) for an overview). The near-symmetric behaviour of the production
$\int \mathcal {P}\sim \varepsilon /k$ (see Poinsot & Veynante (Reference Poinsot and Veynante2005) for an overview). The near-symmetric behaviour of the production ![]() $\int \mathcal {P}$ and destruction
$\int \mathcal {P}$ and destruction ![]() $\int \mathcal {D}$ would suggest that the destruction is also linked to the kinetic energy dissipation rate
$\int \mathcal {D}$ would suggest that the destruction is also linked to the kinetic energy dissipation rate ![]() $\mathcal {E}$. In the present DNS, there is also a strong relationship between the scalar dissipation rate
$\mathcal {E}$. In the present DNS, there is also a strong relationship between the scalar dissipation rate ![]() $\mathcal {X}$ and both the production and destruction of iso-surface area, which is expected from the relationship between
$\mathcal {X}$ and both the production and destruction of iso-surface area, which is expected from the relationship between ![]() $\varSigma$ and
$\varSigma$ and ![]() $\varPhi$. Interestingly, for
$\varPhi$. Interestingly, for ![]() $\varPhi _{iso}=0.95$, there is better qualitative agreement between
$\varPhi _{iso}=0.95$, there is better qualitative agreement between ![]() $\int \mathcal {P}$ and the scalar dissipation rate
$\int \mathcal {P}$ and the scalar dissipation rate ![]() $\mathcal {X}$ during the transitions to turbulence, i.e.
$\mathcal {X}$ during the transitions to turbulence, i.e. ![]() $t\,\Delta U/h_0<100$.
$t\,\Delta U/h_0<100$.
During the self-similar period (![]() $t\,\Delta U/h_0 > 250$), the production and destruction terms are significantly larger than their difference, which is consistent with previous studies of iso-surface area transport (Han & Huh Reference Han and Huh2008; Blakeley et al. Reference Blakeley, Wang and Riley2019; Neamtu-Halic et al. Reference Neamtu-Halic, Krug, Mollicone, Reeuwijk, Haller and Holzner2020; Kulkarni & Bisetti Reference Kulkarni and Bisetti2021). This, coupled with the similarity to
$t\,\Delta U/h_0 > 250$), the production and destruction terms are significantly larger than their difference, which is consistent with previous studies of iso-surface area transport (Han & Huh Reference Han and Huh2008; Blakeley et al. Reference Blakeley, Wang and Riley2019; Neamtu-Halic et al. Reference Neamtu-Halic, Krug, Mollicone, Reeuwijk, Haller and Holzner2020; Kulkarni & Bisetti Reference Kulkarni and Bisetti2021). This, coupled with the similarity to ![]() $\mathcal {E}$ and
$\mathcal {E}$ and ![]() $\mathcal {X}$ above, might suggest that the total iso-surface area is independent of the mixing layer width, i.e. is constant in time. Interestingly, this does not tell the whole story;
$\mathcal {X}$ above, might suggest that the total iso-surface area is independent of the mixing layer width, i.e. is constant in time. Interestingly, this does not tell the whole story; ![]() ${\rm d}A_{iso}/{\rm d}t$ is small, but not zero, during the self-similar period of evolution, as evidenced by the slight but noticeable increase of
${\rm d}A_{iso}/{\rm d}t$ is small, but not zero, during the self-similar period of evolution, as evidenced by the slight but noticeable increase of ![]() $A_{iso}$ over time in figure 3(a). In the following subsections, this seeming discrepancy will be investigated in more detail.
$A_{iso}$ over time in figure 3(a). In the following subsections, this seeming discrepancy will be investigated in more detail.
5.2. Iso-surface area density
Consider now the mean iso-surface area density transport, given by (3.8), subject to the iso-surface averaging methods discussed in § 3.2. The rate of change of iso-surface area density is determined by the production and destruction of ![]() $\varSigma$ as discussed previously, as well as advective and diffusive transport, i.e.
$\varSigma$ as discussed previously, as well as advective and diffusive transport, i.e. ![]() $\partial \varSigma /\partial t = \mathcal {T}_U + \mathcal {P} + \mathcal {T}_D - \mathcal {D}$. Similar to arguments in the previous subsection, an estimate of
$\partial \varSigma /\partial t = \mathcal {T}_U + \mathcal {P} + \mathcal {T}_D - \mathcal {D}$. Similar to arguments in the previous subsection, an estimate of ![]() $\partial \varSigma /\partial t$ is obtained via an explicit finite difference approximation of the
$\partial \varSigma /\partial t$ is obtained via an explicit finite difference approximation of the ![]() $\varSigma (y,t)$ profiles, computed from the DNS data. Note that due to storage constraints, the full three-dimensional DNS fields are available only every 200 physical time steps, significantly limiting the temporal accuracy of the approximation. Nonetheless, it is a useful tool to determine the overall behaviour of the time derivative of
$\varSigma (y,t)$ profiles, computed from the DNS data. Note that due to storage constraints, the full three-dimensional DNS fields are available only every 200 physical time steps, significantly limiting the temporal accuracy of the approximation. Nonetheless, it is a useful tool to determine the overall behaviour of the time derivative of ![]() $\varSigma$, and to test the accuracy of the results by comparing the time derivative to the right-hand side of the equation.
$\varSigma$, and to test the accuracy of the results by comparing the time derivative to the right-hand side of the equation.
Cross-stream profiles of each term are displayed in figures 5(a,c) at ![]() $t\,\Delta U/h_0=462$ for
$t\,\Delta U/h_0=462$ for ![]() $\varPhi _{iso} = 0.5$ and
$\varPhi _{iso} = 0.5$ and ![]() $0.95$, respectively. The terms have been non-dimensionalized by the mixing layer width and the velocity difference
$0.95$, respectively. The terms have been non-dimensionalized by the mixing layer width and the velocity difference ![]() $\Delta U/h^2$. It can be seen that, similar to the results of figure 4,
$\Delta U/h^2$. It can be seen that, similar to the results of figure 4, ![]() $\mathcal {P}$ and
$\mathcal {P}$ and ![]() $\mathcal {D}$ are significantly larger than the remaining terms in the balance equation. Indeed, for
$\mathcal {D}$ are significantly larger than the remaining terms in the balance equation. Indeed, for ![]() $\varPhi _{iso}=0.5$,
$\varPhi _{iso}=0.5$, ![]() $\mathcal {P}$ and
$\mathcal {P}$ and ![]() $\mathcal {D}$ are a full order of magnitude larger than
$\mathcal {D}$ are a full order of magnitude larger than ![]() $\partial \varSigma /\partial t$.
$\partial \varSigma /\partial t$.

Figure 5. Cross-stream profiles of each term in (3.8), for (a,b) ![]() $\varPhi _{iso}=0.5$ and (c,d)
$\varPhi _{iso}=0.5$ and (c,d) ![]() $\varPhi _{iso}=0.95$, at a non-dimensional time at
$\varPhi _{iso}=0.95$, at a non-dimensional time at ![]() $t\,\Delta U/h_0=462$. Blue circles indicate
$t\,\Delta U/h_0=462$. Blue circles indicate ![]() $\partial \varSigma /\partial t$, orange squares indicate
$\partial \varSigma /\partial t$, orange squares indicate ![]() $\mathcal {T}_U$, green up-triangle indicate
$\mathcal {T}_U$, green up-triangle indicate ![]() $\mathcal {P}$, red pentagons indicate
$\mathcal {P}$, red pentagons indicate ![]() $\mathcal {T_D}$, purple down-triangles indicate
$\mathcal {T_D}$, purple down-triangles indicate ![]() $\mathcal {D}$ and turquoise diamonds indicate
$\mathcal {D}$ and turquoise diamonds indicate ![]() $K$, where
$K$, where ![]() $K$ is given by (5.4). The dotted brown line is the sum of the terms on the right-hand side of (3.8). Note the difference in scales between (a,b) and between (c,d).
$K$ is given by (5.4). The dotted brown line is the sum of the terms on the right-hand side of (3.8). Note the difference in scales between (a,b) and between (c,d).
Rather than plotting ![]() $\mathcal {P}$ and
$\mathcal {P}$ and ![]() $\mathcal {D}$ separately, consider instead the net effect of the production and destruction terms,
$\mathcal {D}$ separately, consider instead the net effect of the production and destruction terms,
where ![]() $K$ has been described in the literature as the ‘net surface stretch’ (Candel & Poinsot Reference Candel and Poinsot1990; Kulkarni et al. Reference Kulkarni, Buttay, Kasbaoui, Attili and Bisetti2021). The net surface stretch K is plotted in figures 5(b,d) in place of
$K$ has been described in the literature as the ‘net surface stretch’ (Candel & Poinsot Reference Candel and Poinsot1990; Kulkarni et al. Reference Kulkarni, Buttay, Kasbaoui, Attili and Bisetti2021). The net surface stretch K is plotted in figures 5(b,d) in place of ![]() $\mathcal{P}$ and
$\mathcal{P}$ and ![]() $\mathcal{D}$ for the same time and iso-values as in figures 5(a,c). This comparison demonstrates that the difference between the production and destruction terms is of the same order of magnitude as
$\mathcal{D}$ for the same time and iso-values as in figures 5(a,c). This comparison demonstrates that the difference between the production and destruction terms is of the same order of magnitude as ![]() $\partial \varSigma /\partial t$ and the advective transport
$\partial \varSigma /\partial t$ and the advective transport ![]() $\mathcal {T}_U$; the diffusive transport term
$\mathcal {T}_U$; the diffusive transport term ![]() $\mathcal {T}_D$ is an order of magnitude smaller still. This has significant implications when estimating the self-similar evolution of each term, as described in the following sections.
$\mathcal {T}_D$ is an order of magnitude smaller still. This has significant implications when estimating the self-similar evolution of each term, as described in the following sections.
The comparison between the left-hand and right-hand sides of (3.8) is included in figure 5 to give some idea of the accuracy of the numerical methodology used in the present study. To the authors’ knowledge, few (if any) studies have been able to compare directly the left-hand and right-hand sides of the iso-surface transport equation in a turbulent flow, due in part to the computational demand of traditional iso-surface integration methods and the temporal resolution required to estimate time derivatives. There is general agreement between the two sides of the equation, although some discrepancy exists between the temporal derivative of ![]() $\varSigma$ near
$\varSigma$ near ![]() $y=0$ compared to the right-hand side (see figure 5b). It is expected that this error is caused mainly by taking the difference between two large quantities,
$y=0$ compared to the right-hand side (see figure 5b). It is expected that this error is caused mainly by taking the difference between two large quantities, ![]() $\mathcal {P}$ and
$\mathcal {P}$ and ![]() $\mathcal {D}$, each with its own errors, which are then magnified in computing this difference. Note the difference in scale between figures 5(a,b). Also note that there is considerably less discrepancy between the left-hand and right-hand sides near the boundary of the mixing layer (shown in figure 5d), where terms
$\mathcal {D}$, each with its own errors, which are then magnified in computing this difference. Note the difference in scale between figures 5(a,b). Also note that there is considerably less discrepancy between the left-hand and right-hand sides near the boundary of the mixing layer (shown in figure 5d), where terms ![]() $\mathcal {P}$ and
$\mathcal {P}$ and ![]() $\mathcal {D}$ are not nearly as large.
$\mathcal {D}$ are not nearly as large.
6. Self-similarity of transport terms
Based on the robust self-similar behaviour of ![]() $\varSigma$ in the present DNS (see figure 3), it is thought that the terms in the transport equation for
$\varSigma$ in the present DNS (see figure 3), it is thought that the terms in the transport equation for ![]() $\varSigma$ may also exhibit self-similarity. Self-similar forms for each of the terms in (3.8) (in order, from left to right) are proposed in this section, based on a combination of physical arguments and empirical observations from the DNS data, i.e. how well the instantaneous profiles collapse onto a single curve. Specifically, a number of different combinations of variables are tested for each term, and the standard deviation between the instantaneous profiles and the average over the entire self-similar region is calculated. For brevity, only the scalings that result in the lowest relative deviation from the self-similar average are presented below. Additionally, only results from iso-values
$\varSigma$ may also exhibit self-similarity. Self-similar forms for each of the terms in (3.8) (in order, from left to right) are proposed in this section, based on a combination of physical arguments and empirical observations from the DNS data, i.e. how well the instantaneous profiles collapse onto a single curve. Specifically, a number of different combinations of variables are tested for each term, and the standard deviation between the instantaneous profiles and the average over the entire self-similar region is calculated. For brevity, only the scalings that result in the lowest relative deviation from the self-similar average are presented below. Additionally, only results from iso-values ![]() $\varPhi_{iso} = 0.5$ and 0.95 will be presented in the main text; results from additional iso-values can be found in Appendix A.
$\varPhi_{iso} = 0.5$ and 0.95 will be presented in the main text; results from additional iso-values can be found in Appendix A.
The proposed self-similar forms should be viewed with some scepticism; this is the first time (to the authors’ knowledge) that the spatial dependence of the terms in the transport equation for ![]() $\varSigma$ has been presented, and further refinements of the scaling arguments proposed here are both welcome and expected. The self-similar scalings observed in the present study will be compared to proposed scalings from previous studies when applicable.
$\varSigma$ has been presented, and further refinements of the scaling arguments proposed here are both welcome and expected. The self-similar scalings observed in the present study will be compared to proposed scalings from previous studies when applicable.
6.1. Rate of change of iso-surface area density
The self-similar behaviour of ![]() $\partial \varSigma /\partial t$ is examined in the context of the self-similar behaviour of
$\partial \varSigma /\partial t$ is examined in the context of the self-similar behaviour of ![]() $\varSigma$, which was suggested recently by Blakeley et al. (Reference Blakeley, Olson and Riley2022) to be
$\varSigma$, which was suggested recently by Blakeley et al. (Reference Blakeley, Olson and Riley2022) to be
Therefore, the time derivative of ![]() $\varSigma$ can be expressed as
$\varSigma$ can be expressed as
 \begin{equation} \frac{\partial \varSigma}{\partial t}(y,t) =-\frac{1}{h\lambda_\phi}\,\frac{{\rm d}h}{{\rm d}t}\,\frac{{\rm d}\hat{\varSigma}}{{\rm d}\xi}\,\xi -\frac{1}{\lambda_\phi^2}\,\frac{{\rm d}\lambda_\phi}{{\rm d}t}\,\hat{\varSigma}. \end{equation}
\begin{equation} \frac{\partial \varSigma}{\partial t}(y,t) =-\frac{1}{h\lambda_\phi}\,\frac{{\rm d}h}{{\rm d}t}\,\frac{{\rm d}\hat{\varSigma}}{{\rm d}\xi}\,\xi -\frac{1}{\lambda_\phi^2}\,\frac{{\rm d}\lambda_\phi}{{\rm d}t}\,\hat{\varSigma}. \end{equation}Focusing only on the dimensional coefficient of the first term (for now), the following self-similar scaling is proposed:
 \begin{equation} \frac{\partial \varSigma}{\partial t} = \frac{\Delta U}{h\lambda_\phi}\,\widehat{\frac{\partial \varSigma}{\partial t}}, \end{equation}
\begin{equation} \frac{\partial \varSigma}{\partial t} = \frac{\Delta U}{h\lambda_\phi}\,\widehat{\frac{\partial \varSigma}{\partial t}}, \end{equation}where
will be used as shorthand notation for the self-similar form of the time derivative of ![]() $\varSigma$. Note that the velocity difference
$\varSigma$. Note that the velocity difference ![]() $\Delta U$ has been substituted in place of
$\Delta U$ has been substituted in place of ![]() ${\rm d}h/{\rm d}t$ because it of its ubiquity in self-similar arguments from the literature (despite the fact that
${\rm d}h/{\rm d}t$ because it of its ubiquity in self-similar arguments from the literature (despite the fact that ![]() ${\rm d}h/{\rm d}t$ is arguably a more appropriate metric; Baltzer & Livescu Reference Baltzer and Livescu2020). Due to the linear development of
${\rm d}h/{\rm d}t$ is arguably a more appropriate metric; Baltzer & Livescu Reference Baltzer and Livescu2020). Due to the linear development of ![]() $h$ in the self-similar region,
$h$ in the self-similar region, ![]() $\Delta U$ and
$\Delta U$ and ![]() ${\rm d}h/{\rm d}t$ are proportional to each other in the present simulation.
${\rm d}h/{\rm d}t$ are proportional to each other in the present simulation.
Several instantaneous profiles of ![]() ${\rm d}\varSigma/{\rm d}t$ are plotted in figure 6. The instantaneous profiles are spatially averaged as in (2.1), non-dimensionalized by
${\rm d}\varSigma/{\rm d}t$ are plotted in figure 6. The instantaneous profiles are spatially averaged as in (2.1), non-dimensionalized by ![]() $h\lambda_\phi/U$, and compared to the average value over the entire self-similar period. For
$h\lambda_\phi/U$, and compared to the average value over the entire self-similar period. For ![]() $\varPhi _{iso}=0.95$, the
$\varPhi _{iso}=0.95$, the ![]() $y$ profiles appear to collapse onto the self-similar average. For the iso-value
$y$ profiles appear to collapse onto the self-similar average. For the iso-value ![]() $\varPhi _{iso}=0.5$, however, the self-similar collapse is not as good, with significant fluctuations observed around the mean profile. Note that from the symmetry in the problem initial conditions, these curves should be symmetric about
$\varPhi _{iso}=0.5$, however, the self-similar collapse is not as good, with significant fluctuations observed around the mean profile. Note that from the symmetry in the problem initial conditions, these curves should be symmetric about ![]() $y/h = 0$; this lack of symmetry gives an idea of the statistical error in the measurement. As discussed above, this error is expected to be caused by the limited temporal resolution available to be used in the numerical approximation of
$y/h = 0$; this lack of symmetry gives an idea of the statistical error in the measurement. As discussed above, this error is expected to be caused by the limited temporal resolution available to be used in the numerical approximation of ![]() $\partial \varSigma /\partial t$.
$\partial \varSigma /\partial t$.

Figure 6. Proposed self-similar scaling of ![]() $\partial \varSigma /\partial t$ from (3.8), conditioned on (a)
$\partial \varSigma /\partial t$ from (3.8), conditioned on (a) ![]() $\varPhi _{iso}=0.5$ and (b)
$\varPhi _{iso}=0.5$ and (b) ![]() $\varPhi _{iso}=0.95$, as functions of the similarity variable
$\varPhi _{iso}=0.95$, as functions of the similarity variable ![]() $\xi =y/h$. The solid line refers to the time average over the entire self-similar period, and dashed lines refer to instantaneous profiles, spatially averaged as in (2.1).
$\xi =y/h$. The solid line refers to the time average over the entire self-similar period, and dashed lines refer to instantaneous profiles, spatially averaged as in (2.1).
Consider now the second term on the right-hand side of (6.2), which is expected to exhibit the same scaling properties as the first term on the right-hand side. Beginning from (4.8), the self-similar scaling of the scalar Taylor length scale is expected to be ![]() $\lambda _\phi \sim (hD/\Delta U)^{1/2}$, based on the self-similar scalings of
$\lambda _\phi \sim (hD/\Delta U)^{1/2}$, based on the self-similar scalings of ![]() $\left \langle \phi ^2 \right \rangle$ and
$\left \langle \phi ^2 \right \rangle$ and ![]() $\chi$. Substituting this scaling for
$\chi$. Substituting this scaling for ![]() $\lambda _\phi$ into the second term on the right-hand side of (6.2) yields the expression
$\lambda _\phi$ into the second term on the right-hand side of (6.2) yields the expression
 \begin{equation} \frac{1}{\lambda_\phi^2}\,\frac{{\rm d}\lambda_\phi}{{\rm d}t} \sim \frac{\Delta U}{hD}\left(\frac{D}{\Delta U}\right)^{1/2}\frac{h^{-1/2}}{2}\,\frac{\mathrm{d}h}{\mathrm{d}t} \sim \frac{\Delta U}{h}\left(\frac{\Delta U}{hD}\right)^{1/2}\sim\frac{\Delta U}{h\lambda_\phi}, \end{equation}
\begin{equation} \frac{1}{\lambda_\phi^2}\,\frac{{\rm d}\lambda_\phi}{{\rm d}t} \sim \frac{\Delta U}{hD}\left(\frac{D}{\Delta U}\right)^{1/2}\frac{h^{-1/2}}{2}\,\frac{\mathrm{d}h}{\mathrm{d}t} \sim \frac{\Delta U}{h}\left(\frac{\Delta U}{hD}\right)^{1/2}\sim\frac{\Delta U}{h\lambda_\phi}, \end{equation}which is identical to the self-similar scaling found in (6.3).
Importantly, the above scaling argument also suggests that the self-similar development of ![]() $\lambda _\phi$ is proportional to
$\lambda _\phi$ is proportional to ![]() $h^{1/2}$, which can also be verified by the DNS data. The temporal evolution of
$h^{1/2}$, which can also be verified by the DNS data. The temporal evolution of ![]() $\lambda _\phi h^{-1/2}$ is plotted in figure 7(a) and can be seen to approach a constant value in the self-similar period, consistent with the proposed scaling argument. In addition to
$\lambda _\phi h^{-1/2}$ is plotted in figure 7(a) and can be seen to approach a constant value in the self-similar period, consistent with the proposed scaling argument. In addition to ![]() $\lambda _\phi$, the transverse Taylor and Kolmogorov scales are also plotted with the appropriate self-similar scaling applied.
$\lambda _\phi$, the transverse Taylor and Kolmogorov scales are also plotted with the appropriate self-similar scaling applied.

Figure 7. (a) Self-similar development of Taylor and Kolmogorov microscales compared to predictions from self-similarity. (b,c) Self-similar profile of ![]() $\partial \varSigma /\partial t$ normalized by
$\partial \varSigma /\partial t$ normalized by ![]() $h\lambda _\phi /\Delta U$ compared to the predicted self-similar profile assuming that
$h\lambda _\phi /\Delta U$ compared to the predicted self-similar profile assuming that ![]() $\varSigma$ is Gaussian (dashed line) and the sum of terms on the right-hand side of (3.8) (dotted line) for (b)
$\varSigma$ is Gaussian (dashed line) and the sum of terms on the right-hand side of (3.8) (dotted line) for (b) ![]() $\varPhi _{iso}=0.5$ and (c)
$\varPhi _{iso}=0.5$ and (c) ![]() $\varPhi _{iso}=0.95$.
$\varPhi _{iso}=0.95$.
To further test the assumed self-similar form for the profile of ![]() $\partial \varSigma /\partial t$, it is compared to the right-hand side of (3.8), normalized by
$\partial \varSigma /\partial t$, it is compared to the right-hand side of (3.8), normalized by ![]() $h\lambda _\phi /\Delta U$, in figure 7. The self-similar profiles of the right-hand side of (3.8) (dotted line) demonstrate the correct behaviour for both iso-values plotted, although there are significant differences near the peaks of the curves for
$h\lambda _\phi /\Delta U$, in figure 7. The self-similar profiles of the right-hand side of (3.8) (dotted line) demonstrate the correct behaviour for both iso-values plotted, although there are significant differences near the peaks of the curves for ![]() $\varPhi = 0.5$. This is similar to what was seen in figures 5(b,d).
$\varPhi = 0.5$. This is similar to what was seen in figures 5(b,d).
As a second test, an approximation from a previous study (Blakeley et al. Reference Blakeley, Olson and Riley2022) can be leveraged to study the self-similar development of ![]() $\partial \varSigma /\partial t$. For the temporal mixing layer presented here,
$\partial \varSigma /\partial t$. For the temporal mixing layer presented here, ![]() $\hat {\varSigma }$ can be approximated with a Gaussian profile, i.e.
$\hat {\varSigma }$ can be approximated with a Gaussian profile, i.e.
where ![]() $\hat {\varSigma }_m$,
$\hat {\varSigma }_m$, ![]() $\xi _m$ and
$\xi _m$ and ![]() $\hat {\sigma }$ are the peak value, location of peak value and standard deviation of
$\hat {\sigma }$ are the peak value, location of peak value and standard deviation of ![]() $\hat {\varSigma }$ in the self-similar coordinates (Blakeley et al. Reference Blakeley, Olson and Riley2022). Substituting the above expression for
$\hat {\varSigma }$ in the self-similar coordinates (Blakeley et al. Reference Blakeley, Olson and Riley2022). Substituting the above expression for ![]() $\hat {\varSigma }(\xi )$ into (6.2), and using the values of
$\hat {\varSigma }(\xi )$ into (6.2), and using the values of ![]() $h$,
$h$, ![]() ${\rm d}h/{\rm d}t$,
${\rm d}h/{\rm d}t$, ![]() $\lambda _\phi$ and
$\lambda _\phi$ and ![]() ${\rm d}\lambda _\phi /{\rm d}t$ from the present DNS, yields the dashed line in figures 7(b,c). The behaviour of the Gaussian model is qualitatively correct, although there are discrepancies near the peaks of the curve.
${\rm d}\lambda _\phi /{\rm d}t$ from the present DNS, yields the dashed line in figures 7(b,c). The behaviour of the Gaussian model is qualitatively correct, although there are discrepancies near the peaks of the curve.
6.2. Advective transport
Next, consider ![]() $\mathcal {T}_U = -(\partial /\partial x_i)(\left \langle U_i \right \rangle _s\varSigma )$, which describes the transport of
$\mathcal {T}_U = -(\partial /\partial x_i)(\left \langle U_i \right \rangle _s\varSigma )$, which describes the transport of ![]() $\varSigma$ due to the velocity field. This can be decomposed into mean and fluctuating components
$\varSigma$ due to the velocity field. This can be decomposed into mean and fluctuating components ![]() $\mathcal {T}_m$ and
$\mathcal {T}_m$ and ![]() $\mathcal {T}_t$:
$\mathcal {T}_t$:
 \begin{equation} \frac{\partial }{\partial x_i}\left(\left\langle U_i \right\rangle_s\varSigma\right) = \underbrace{\frac{\partial }{\partial x_i}\left(\left\langle U_i \right\rangle\varSigma\right)}_{\mathcal{T}_m} + \underbrace{\frac{\partial }{\partial x_i}\left(\left\langle u_i \right\rangle_s\varSigma\right)}_{\mathcal{T}_t}, \end{equation}
\begin{equation} \frac{\partial }{\partial x_i}\left(\left\langle U_i \right\rangle_s\varSigma\right) = \underbrace{\frac{\partial }{\partial x_i}\left(\left\langle U_i \right\rangle\varSigma\right)}_{\mathcal{T}_m} + \underbrace{\frac{\partial }{\partial x_i}\left(\left\langle u_i \right\rangle_s\varSigma\right)}_{\mathcal{T}_t}, \end{equation}
where ![]() $\left \langle u_i \right \rangle _s$ is the surface average of the fluctuating component of velocity
$\left \langle u_i \right \rangle _s$ is the surface average of the fluctuating component of velocity ![]() $u_i$. Due to the geometry of the mixing layer, only the cross-stream velocity
$u_i$. Due to the geometry of the mixing layer, only the cross-stream velocity ![]() $V$ will contribute to
$V$ will contribute to ![]() $\mathcal {T}_U$. Furthermore, it can be shown from conservation of mass and the free-slip boundary conditions that the mean cross-stream velocity,
$\mathcal {T}_U$. Furthermore, it can be shown from conservation of mass and the free-slip boundary conditions that the mean cross-stream velocity, ![]() $\left \langle V \right \rangle$, must be zero for all values of
$\left \langle V \right \rangle$, must be zero for all values of ![]() $y$. Thus the effect of the velocity field on the rate of change of
$y$. Thus the effect of the velocity field on the rate of change of ![]() $\varSigma$ is due entirely to the turbulent fluctuations of the cross-stream velocity
$\varSigma$ is due entirely to the turbulent fluctuations of the cross-stream velocity ![]() $v$, and hence the turbulent flux
$v$, and hence the turbulent flux ![]() $\mathcal {T}_t$.
$\mathcal {T}_t$.
To estimate how ![]() $\mathcal {T}_t$ will evolve in the self-similar region, it is reasonable to assume that the surface-averaged velocity fluctuations
$\mathcal {T}_t$ will evolve in the self-similar region, it is reasonable to assume that the surface-averaged velocity fluctuations ![]() $\left \langle u_i \right \rangle _s$ will scale similar to the root mean square (r.m.s.) velocity
$\left \langle u_i \right \rangle _s$ will scale similar to the root mean square (r.m.s.) velocity ![]() $\left \langle u_iu_i \right \rangle ^{1/2}$, which is known to scale with the velocity difference
$\left \langle u_iu_i \right \rangle ^{1/2}$, which is known to scale with the velocity difference ![]() $\Delta U$ (Rogers & Moser Reference Rogers and Moser1994). By noting that
$\Delta U$ (Rogers & Moser Reference Rogers and Moser1994). By noting that ![]() $\varSigma \sim \lambda _\phi$ (see figures 3b,c) and assuming that the cross-stream derivative will scale with the mixing width, i.e.
$\varSigma \sim \lambda _\phi$ (see figures 3b,c) and assuming that the cross-stream derivative will scale with the mixing width, i.e. ![]() $\partial /\partial y\sim 1/h$, the self-similar form of
$\partial /\partial y\sim 1/h$, the self-similar form of ![]() $\mathcal {T}_t$ should be
$\mathcal {T}_t$ should be
The proposed scaling for ![]() $\mathcal {T}_t$ results in a collapse of the instantaneous profiles on the self-similar form for
$\mathcal {T}_t$ results in a collapse of the instantaneous profiles on the self-similar form for ![]() $\partial \varSigma /\partial t$ in (6.3), suggesting that the scaling is consistent with the DNS data. Additionally, these results agree with the findings from Kulkarni & Bisetti (Reference Kulkarni and Bisetti2021), who found that the turbulent transport term (normalized by
$\partial \varSigma /\partial t$ in (6.3), suggesting that the scaling is consistent with the DNS data. Additionally, these results agree with the findings from Kulkarni & Bisetti (Reference Kulkarni and Bisetti2021), who found that the turbulent transport term (normalized by ![]() $\varSigma$) scales with the integral length scale of the flow.
$\varSigma$) scales with the integral length scale of the flow.
The self-similar profiles of ![]() $\mathcal {T}_t$ are plotted in figure 8. Apart from small fluctuations around the peaks of the curves, the instantaneous profiles collapse onto a single curve for the assumed self-similar form, suggesting that (6.8) is the appropriate scaling for
$\mathcal {T}_t$ are plotted in figure 8. Apart from small fluctuations around the peaks of the curves, the instantaneous profiles collapse onto a single curve for the assumed self-similar form, suggesting that (6.8) is the appropriate scaling for ![]() $\mathcal {T}_t$ for this temporal turbulent mixing layer.
$\mathcal {T}_t$ for this temporal turbulent mixing layer.
These data also suggest that the turbulent transport for the iso-surface corresponding to ![]() $\varPhi _{iso}=0.5$ acts in a traditional gradient-diffusive manner (Veynante et al. Reference Veynante, Trouvé, Bray and Mantel1997), acting to remove
$\varPhi _{iso}=0.5$ acts in a traditional gradient-diffusive manner (Veynante et al. Reference Veynante, Trouvé, Bray and Mantel1997), acting to remove ![]() $\varSigma$ from the peak and diffuse it outwards. In fact, for a constant, non-dimensional turbulent diffusivity
$\varSigma$ from the peak and diffuse it outwards. In fact, for a constant, non-dimensional turbulent diffusivity ![]() $\hat {D}_t=0.015$, it can be shown that the assumption
$\hat {D}_t=0.015$, it can be shown that the assumption
gives an excellent match when ![]() $\varPhi _{iso}=0.5$, as shown in figure 9(a). For
$\varPhi _{iso}=0.5$, as shown in figure 9(a). For ![]() $\varPhi _{iso}=0.95$, where the iso-surface is located, on average, away from the centreline, the turbulent transport is still diffusive in nature by removing
$\varPhi _{iso}=0.95$, where the iso-surface is located, on average, away from the centreline, the turbulent transport is still diffusive in nature by removing ![]() $\varSigma$ from the local peak. However, the diffusion is preferentially towards the centre of the mixing layer, rather than away from the centreline as might be expected. In this case, the assumption of a constant turbulent diffusivity is clearly incorrect, as demonstrated by the significant discrepancy between the two curves in figure 9(b). It is thought that the preferential diffusion towards the centreline is due to the fact that the turbulent fluctuations are greatest near
$\varSigma$ from the local peak. However, the diffusion is preferentially towards the centre of the mixing layer, rather than away from the centreline as might be expected. In this case, the assumption of a constant turbulent diffusivity is clearly incorrect, as demonstrated by the significant discrepancy between the two curves in figure 9(b). It is thought that the preferential diffusion towards the centreline is due to the fact that the turbulent fluctuations are greatest near ![]() $y/h=0$ (see e.g. figure 2a) and decay quickly to zero near the edge of the mixing layer. This could, perhaps, be accounted for in the turbulent diffusivity by choosing the standard form
$y/h=0$ (see e.g. figure 2a) and decay quickly to zero near the edge of the mixing layer. This could, perhaps, be accounted for in the turbulent diffusivity by choosing the standard form ![]() $D_t=\alpha u' \ell$, where
$D_t=\alpha u' \ell$, where ![]() $\alpha$ is a constant,
$\alpha$ is a constant, ![]() $u'$ is the r.m.s. of the velocity fluctuations, and
$u'$ is the r.m.s. of the velocity fluctuations, and ![]() $\ell$ is a characteristic length (Pope Reference Pope2000), or by a two-equation model that better approximates the inhomogeneous nature of the turbulent fluctuations. Although this will not be investigated further in the present study, it should be emphasized that care should be taken in modelling the turbulent flux of an iso-surface, as the behaviour of
$\ell$ is a characteristic length (Pope Reference Pope2000), or by a two-equation model that better approximates the inhomogeneous nature of the turbulent fluctuations. Although this will not be investigated further in the present study, it should be emphasized that care should be taken in modelling the turbulent flux of an iso-surface, as the behaviour of ![]() $\mathcal {T}_t$ exhibits a strong dependence on the iso-value chosen in the present configuration.
$\mathcal {T}_t$ exhibits a strong dependence on the iso-value chosen in the present configuration.

Figure 9. Cross-stream profile of the surface weighted velocity ![]() $\left \langle v\varSigma ' \right \rangle$ in the self-similar period, compared to the gradient-diffusion hypothesis in (6.9), assuming constant turbulent diffusivity
$\left \langle v\varSigma ' \right \rangle$ in the self-similar period, compared to the gradient-diffusion hypothesis in (6.9), assuming constant turbulent diffusivity ![]() $\hat {D}_t=0.015$, for (a)
$\hat {D}_t=0.015$, for (a) ![]() $\varPhi _{iso}=0.5$ and (b)
$\varPhi _{iso}=0.5$ and (b) ![]() $\varPhi _{iso}=0.95$.
$\varPhi _{iso}=0.95$.
6.3. Production
Consider the term responsible for production of iso-surface area due to the fluid strain rate ![]() $\mathcal {P} = -\left \langle n_in_jS_{ij} \right \rangle _s\varSigma$. Self-similar scaling for this term can be deduced by considering that the correlation tangential strain rate of the scalar field,
$\mathcal {P} = -\left \langle n_in_jS_{ij} \right \rangle _s\varSigma$. Self-similar scaling for this term can be deduced by considering that the correlation tangential strain rate of the scalar field, ![]() $\left \langle n_in_jS_{ij} \right \rangle _s$, has been shown to scale with the mean turbulent strain rate
$\left \langle n_in_jS_{ij} \right \rangle _s$, has been shown to scale with the mean turbulent strain rate ![]() $(\varepsilon /\upsilon )^{1/2}$ (Poinsot & Veynante Reference Poinsot and Veynante2005; Kulkarni & Bisetti Reference Kulkarni and Bisetti2021). Based on the definition of the transverse Taylor length scale in (4.7), and noting that
$(\varepsilon /\upsilon )^{1/2}$ (Poinsot & Veynante Reference Poinsot and Veynante2005; Kulkarni & Bisetti Reference Kulkarni and Bisetti2021). Based on the definition of the transverse Taylor length scale in (4.7), and noting that ![]() $u_{rms}\sim \Delta U$ in the present temporal mixing layer, it can be shown that
$u_{rms}\sim \Delta U$ in the present temporal mixing layer, it can be shown that ![]() $\lambda _g/\Delta U\sim (\varepsilon /\upsilon )^{-1/2}$. This implies that the tangential strain rate
$\lambda _g/\Delta U\sim (\varepsilon /\upsilon )^{-1/2}$. This implies that the tangential strain rate ![]() $\left \langle n_in_jS_{ij} \right \rangle _s$ scales approximately with
$\left \langle n_in_jS_{ij} \right \rangle _s$ scales approximately with ![]() $\lambda _g/\Delta U$. Recalling that
$\lambda _g/\Delta U$. Recalling that ![]() $\varSigma \sim 1/\lambda _\phi$ and that
$\varSigma \sim 1/\lambda _\phi$ and that ![]() $\lambda _g\sim \lambda _\phi$ in the present study, it is suggested that the production term scales according to
$\lambda _g\sim \lambda _\phi$ in the present study, it is suggested that the production term scales according to
The self-similar profiles for ![]() $\mathcal {P}$ are displayed in figure 10. There is some discrepancy in the width of the profiles for this term, especially near
$\mathcal {P}$ are displayed in figure 10. There is some discrepancy in the width of the profiles for this term, especially near ![]() $y/h=0$ for
$y/h=0$ for ![]() $\varPhi _{iso}=0.95$, although the difference is relatively small.
$\varPhi _{iso}=0.95$, although the difference is relatively small.

Figure 10. Proposed self-similar scaling of ![]() $\mathcal {P} = -\left \langle n_in_jS_{ij} \right \rangle _s\varSigma$ from (6.10), conditioned on (a)
$\mathcal {P} = -\left \langle n_in_jS_{ij} \right \rangle _s\varSigma$ from (6.10), conditioned on (a) ![]() $\varPhi _{iso}=0.5$ and (b)
$\varPhi _{iso}=0.5$ and (b) ![]() $\varPhi _{iso}=0.95$, as functions of the similarity variable
$\varPhi _{iso}=0.95$, as functions of the similarity variable ![]() $\xi =y/h$. Solid and dashed lines are as in figure 6. Note that the magnitude of the peak value of
$\xi =y/h$. Solid and dashed lines are as in figure 6. Note that the magnitude of the peak value of ![]() $\mathcal {P}$ is significantly smaller near the edge of the mixing layer (
$\mathcal {P}$ is significantly smaller near the edge of the mixing layer (![]() $\varPhi _{iso}=0.95$) than it is near the centreline (
$\varPhi _{iso}=0.95$) than it is near the centreline (![]() $\varPhi _{iso}=0.5$).
$\varPhi _{iso}=0.5$).
The self-similar scaling provided here can be used to predict the behaviour of the integrated production term ![]() $\int \mathcal {P}$, discussed in figure 4. Based upon (6.10), the integrated production term is predicted to scale as
$\int \mathcal {P}$, discussed in figure 4. Based upon (6.10), the integrated production term is predicted to scale as ![]() $\int \mathcal {P}\sim \Delta U\,h/\lambda _\phi ^2$, which is independent of time (recall that
$\int \mathcal {P}\sim \Delta U\,h/\lambda _\phi ^2$, which is independent of time (recall that ![]() $\lambda _\phi \sim h^{1/2}$). Qualitatively, this agrees with the observed behaviour of
$\lambda _\phi \sim h^{1/2}$). Qualitatively, this agrees with the observed behaviour of ![]() $\int \mathcal {P}$ from figure 4.
$\int \mathcal {P}$ from figure 4.
6.4. Diffusive transport
Before analysing the diffusive transport term ![]() $\mathcal {T}_D = -\partial (\langle w_{dif} n_i\rangle _s\varSigma )/\partial x_i$, it is helpful to first consider the self-similar behaviour of the surface-averaged diffusion velocity, i.e.
$\mathcal {T}_D = -\partial (\langle w_{dif} n_i\rangle _s\varSigma )/\partial x_i$, it is helpful to first consider the self-similar behaviour of the surface-averaged diffusion velocity, i.e. ![]() $\left \langle w_{dif} n_i \varSigma ' \right \rangle = \left \langle w_{dif} n_i \right \rangle _s\varSigma$. To estimate the self-similar scaling of this term, a characteristic velocity scale for
$\left \langle w_{dif} n_i \varSigma ' \right \rangle = \left \langle w_{dif} n_i \right \rangle _s\varSigma$. To estimate the self-similar scaling of this term, a characteristic velocity scale for ![]() $w_{dif}$ is formed by considering the rate at which a scalar with diffusivity
$w_{dif}$ is formed by considering the rate at which a scalar with diffusivity ![]() $D$ will diffuse over a length
$D$ will diffuse over a length ![]() $\ell$, such that
$\ell$, such that ![]() $w_{dif}\sim D/\ell$. It was determined empirically that choosing
$w_{dif}\sim D/\ell$. It was determined empirically that choosing ![]() $\ell = \lambda _\phi$ results in the least error between instantaneous and self-similar profiles, which suggests that
$\ell = \lambda _\phi$ results in the least error between instantaneous and self-similar profiles, which suggests that ![]() $\left \langle w_{dif} \right \rangle _s\varSigma \sim D/\lambda _\phi ^2$. Because
$\left \langle w_{dif} \right \rangle _s\varSigma \sim D/\lambda _\phi ^2$. Because ![]() $0\leq n_i\leq 1$, it is not expected that the normal vector will affect the self-similar scaling of this term (although it does affect the direction of propagation).
$0\leq n_i\leq 1$, it is not expected that the normal vector will affect the self-similar scaling of this term (although it does affect the direction of propagation).
As shown in figure 11, the instantaneous profiles collapse onto the mean profile of the ![]() $y$ component of the surface-averaged diffusion velocity,
$y$ component of the surface-averaged diffusion velocity, ![]() $\left \langle w_{dif} n_y \right \rangle _s\varSigma$, for the proposed scaling. Note that only the
$\left \langle w_{dif} n_y \right \rangle _s\varSigma$, for the proposed scaling. Note that only the ![]() $y$ component is shown here because it is the only component that contributes to
$y$ component is shown here because it is the only component that contributes to ![]() $\mathcal {T}_D$.
$\mathcal {T}_D$.

Figure 11. Proposed self-similar scaling of ![]() $\langle w_{dif} n_y\rangle _s\varSigma$, conditioned on (a)
$\langle w_{dif} n_y\rangle _s\varSigma$, conditioned on (a) ![]() $\varPhi _{iso}=0.5$ and (b)
$\varPhi _{iso}=0.5$ and (b) ![]() $\varPhi _{iso}=0.95$, as functions of the similarity variable
$\varPhi _{iso}=0.95$, as functions of the similarity variable ![]() $\xi =y/h$. Solid and dashed lines are as in figure 6.
$\xi =y/h$. Solid and dashed lines are as in figure 6.
The behaviour of ![]() $\left \langle w_{dif} n_y \right \rangle _s\varSigma$ in figure 11 is somewhat unintuitive. In figure 11(a), it is observed that the diffusion velocity of the
$\left \langle w_{dif} n_y \right \rangle _s\varSigma$ in figure 11 is somewhat unintuitive. In figure 11(a), it is observed that the diffusion velocity of the ![]() $\varPhi _{iso}=0.5$ iso-surface is positive for
$\varPhi _{iso}=0.5$ iso-surface is positive for ![]() $y/h<0$, and negative for
$y/h<0$, and negative for ![]() $y/h>0$, which will cause
$y/h>0$, which will cause ![]() $\varSigma$ to concentrate at
$\varSigma$ to concentrate at ![]() $y/h=0$. Although it appears to be counterintuitive, this finding is consistent with the linear solution for a pure diffusion problem (i.e. where
$y/h=0$. Although it appears to be counterintuitive, this finding is consistent with the linear solution for a pure diffusion problem (i.e. where ![]() $U=0$). The value of the diffusion velocity for
$U=0$). The value of the diffusion velocity for ![]() $\varPhi _{iso}=0.95$, shown in figure 11(b), is only positive, with a peak value located near the maximum of
$\varPhi _{iso}=0.95$, shown in figure 11(b), is only positive, with a peak value located near the maximum of ![]() $\varSigma (\varPhi _{iso}=0.95)$. This suggests that, on average, the iso-surface associated with
$\varSigma (\varPhi _{iso}=0.95)$. This suggests that, on average, the iso-surface associated with ![]() $\varPhi _{iso}=0.95$ will diffuse in the positive
$\varPhi _{iso}=0.95$ will diffuse in the positive ![]() $y$ direction. This result is notably distinct from the behaviour observed for
$y$ direction. This result is notably distinct from the behaviour observed for ![]() $\varPhi _{iso}=0.5$, but is nonetheless an expected result based on the solution to a purely diffusive problem with zero velocity.
$\varPhi _{iso}=0.5$, but is nonetheless an expected result based on the solution to a purely diffusive problem with zero velocity.
To scale the diffusion term ![]() $\mathcal {T}_D=-\partial (\left \langle w_{dif} n_i \right \rangle _s\varSigma )/\partial x_i$ in (3.8), it is assumed that the derivative in the cross-stream direction introduces a factor
$\mathcal {T}_D=-\partial (\left \langle w_{dif} n_i \right \rangle _s\varSigma )/\partial x_i$ in (3.8), it is assumed that the derivative in the cross-stream direction introduces a factor ![]() $1/h$ to the scaling (similar to the argument for the advective flux
$1/h$ to the scaling (similar to the argument for the advective flux ![]() $\mathcal {T}_U$ in § 6.2). Based on this assumption and the above scaling proposed for
$\mathcal {T}_U$ in § 6.2). Based on this assumption and the above scaling proposed for ![]() $\left \langle w_{dif} n_i \right \rangle _s\varSigma$, the self-similar form of
$\left \langle w_{dif} n_i \right \rangle _s\varSigma$, the self-similar form of ![]() $\mathcal {T}_D$ is given by
$\mathcal {T}_D$ is given by
The results for ![]() $\mathcal {T}_D$ using the above self-similar scaling are displayed in figure 12, demonstrating the collapse of instantaneous profiles onto a single self-similar profile for the proposed scaling above.
$\mathcal {T}_D$ using the above self-similar scaling are displayed in figure 12, demonstrating the collapse of instantaneous profiles onto a single self-similar profile for the proposed scaling above.

Figure 12. Proposed self-similar scaling of term ![]() $\mathcal {T}_D=-\partial (\left \langle w_{dif} n_i \right \rangle _s\varSigma )/\partial x_i$ from (6.11), conditioned on (a)
$\mathcal {T}_D=-\partial (\left \langle w_{dif} n_i \right \rangle _s\varSigma )/\partial x_i$ from (6.11), conditioned on (a) ![]() $\varPhi _{iso}=0.5$ and (b)
$\varPhi _{iso}=0.5$ and (b) ![]() $\varPhi _{iso}=0.95$, as functions of the similarity variable
$\varPhi _{iso}=0.95$, as functions of the similarity variable ![]() $\xi =y/h$. Solid and dashed lines are as in figure 6.
$\xi =y/h$. Solid and dashed lines are as in figure 6.
Similar to the results for the diffusion velocity above, the behaviour of ![]() $\mathcal {T}_D$ is somewhat non-intuitive. Interestingly, for the
$\mathcal {T}_D$ is somewhat non-intuitive. Interestingly, for the ![]() $\varPhi _{iso}=0.5$ iso-surface shown in figure 12(a),
$\varPhi _{iso}=0.5$ iso-surface shown in figure 12(a), ![]() $\mathcal {T}_D$ does not act to spread out or diffuse the profile of
$\mathcal {T}_D$ does not act to spread out or diffuse the profile of ![]() $\varSigma$, but rather acts to concentrate the profile
$\varSigma$, but rather acts to concentrate the profile ![]() $\varSigma$ at the location
$\varSigma$ at the location ![]() $y/h=0$. This finding is consistent with the behaviour of the diffusion velocity discussed previously. The behaviour of
$y/h=0$. This finding is consistent with the behaviour of the diffusion velocity discussed previously. The behaviour of ![]() $\mathcal {T}_D$ for the iso-surface
$\mathcal {T}_D$ for the iso-surface ![]() $\varPhi _{iso}=0.95$, shown in figure 12(b), is responsible for removing
$\varPhi _{iso}=0.95$, shown in figure 12(b), is responsible for removing ![]() $\varSigma$ near the centre of the mixing layer, and transporting it to the outside of the mixing layer. This is consistent with the findings for the diffusion velocity and an intuitive understanding of the iso-surface behaviour.
$\varSigma$ near the centre of the mixing layer, and transporting it to the outside of the mixing layer. This is consistent with the findings for the diffusion velocity and an intuitive understanding of the iso-surface behaviour.
For the present DNS, the magnitude of ![]() $\mathcal {T}_D$ is negligible compared to the other terms (see § 7); as such, the effect of molecular diffusion on
$\mathcal {T}_D$ is negligible compared to the other terms (see § 7); as such, the effect of molecular diffusion on ![]() $\partial \varSigma /\partial t$ is small and will not be investigated further. It should be noted that this term is not expected to be negligible for highly diffusive surfaces (i.e.
$\partial \varSigma /\partial t$ is small and will not be investigated further. It should be noted that this term is not expected to be negligible for highly diffusive surfaces (i.e. ![]() $Sc\ll 1$), or active surfaces such as premixed flames, and will therefore require further study, especially given the non-intuitive behaviour observed herein.
$Sc\ll 1$), or active surfaces such as premixed flames, and will therefore require further study, especially given the non-intuitive behaviour observed herein.
6.5. Destruction
The self-similar development of ![]() $\mathcal {D} = -\left \langle w_{dif}\,\partial n_i/\partial x_i \right \rangle _s\varSigma$ can be understood by invoking a well-known identity that decomposes
$\mathcal {D} = -\left \langle w_{dif}\,\partial n_i/\partial x_i \right \rangle _s\varSigma$ can be understood by invoking a well-known identity that decomposes ![]() $w_{dif}$ into two terms, one related to diffusion in the direction normal to the iso-surface,
$w_{dif}$ into two terms, one related to diffusion in the direction normal to the iso-surface, ![]() $w_N$, and one related to the curvature of the iso-surface,
$w_N$, and one related to the curvature of the iso-surface, ![]() $w_C$ (van Kalmthout & Veynante Reference van Kalmthout and Veynante1998):
$w_C$ (van Kalmthout & Veynante Reference van Kalmthout and Veynante1998):
 \begin{equation} w_{dif} =-\underbrace{\frac{D}{|\boldsymbol{\nabla}\varPhi|}\,\frac{\partial |\boldsymbol{\nabla}\varPhi|}{\partial x_i}\,n_i}_{w_N} -\underbrace{\frac{\partial n_i}{\partial x_i}}_{w_C}. \end{equation}
\begin{equation} w_{dif} =-\underbrace{\frac{D}{|\boldsymbol{\nabla}\varPhi|}\,\frac{\partial |\boldsymbol{\nabla}\varPhi|}{\partial x_i}\,n_i}_{w_N} -\underbrace{\frac{\partial n_i}{\partial x_i}}_{w_C}. \end{equation}
This decomposition can be used to split term ![]() $\mathcal {D}$ into two separate components,
$\mathcal {D}$ into two separate components,
 \begin{equation} \mathcal{D} = \underbrace{\left\langle w_N\,\frac{\partial n_i}{\partial x_i} \right\rangle_s\varSigma}_{\mathcal{D}_a} + \underbrace{D\left\langle \left(\frac{\partial n_i}{\partial x_i}\right)^2 \right\rangle_s\varSigma}_{\mathcal{D}_b}, \end{equation}
\begin{equation} \mathcal{D} = \underbrace{\left\langle w_N\,\frac{\partial n_i}{\partial x_i} \right\rangle_s\varSigma}_{\mathcal{D}_a} + \underbrace{D\left\langle \left(\frac{\partial n_i}{\partial x_i}\right)^2 \right\rangle_s\varSigma}_{\mathcal{D}_b}, \end{equation}
where ![]() $\mathcal {D}_b$ is notable because when substituted into (3.8), it must always take on a negative value in a manner analogous to the dissipation rates
$\mathcal {D}_b$ is notable because when substituted into (3.8), it must always take on a negative value in a manner analogous to the dissipation rates ![]() $\varepsilon$ and
$\varepsilon$ and ![]() $\chi$. In contrast,
$\chi$. In contrast, ![]() $\mathcal {D}_a$ may take on either positive or negative values; in the present DNS,
$\mathcal {D}_a$ may take on either positive or negative values; in the present DNS, ![]() $\mathcal {D}_a$ acts predominantly to destroy iso-surface area density (except for a very slight region on the far outside of the mixing layer). Although some studies have suggested that
$\mathcal {D}_a$ acts predominantly to destroy iso-surface area density (except for a very slight region on the far outside of the mixing layer). Although some studies have suggested that ![]() $\mathcal {D}_a$ is negligible compared to
$\mathcal {D}_a$ is negligible compared to ![]() $\mathcal {D}_b$ (van Kalmthout & Veynante Reference van Kalmthout and Veynante1998), the terms are found to be of comparable magnitude in the present study, as shown in figure 13. Because the two terms are of comparable magnitude over a wide range of iso-values, it is postulated that
$\mathcal {D}_b$ (van Kalmthout & Veynante Reference van Kalmthout and Veynante1998), the terms are found to be of comparable magnitude in the present study, as shown in figure 13. Because the two terms are of comparable magnitude over a wide range of iso-values, it is postulated that ![]() $\mathcal {D}_a$ and
$\mathcal {D}_a$ and ![]() $\mathcal {D}_b$ will evolve together during the self-similar period. This assumption will be used to simplify the scaling argument below for the destruction term.
$\mathcal {D}_b$ will evolve together during the self-similar period. This assumption will be used to simplify the scaling argument below for the destruction term.

Figure 13. Decomposition of term ![]() $\mathcal {D}$ into components related to normal diffusion (
$\mathcal {D}$ into components related to normal diffusion (![]() $V_a$) and curvature (
$V_a$) and curvature (![]() $V_b$) at
$V_b$) at ![]() $t\,\Delta U/h_0=462$, conditioned on (a)
$t\,\Delta U/h_0=462$, conditioned on (a) ![]() $\varPhi _{iso}=0.5$ and (b)
$\varPhi _{iso}=0.5$ and (b) ![]() $\varPhi _{iso}=0.95$. Terms are normalized by the mixing layer width at
$\varPhi _{iso}=0.95$. Terms are normalized by the mixing layer width at ![]() $t\,\Delta U/h=462$ and the velocity difference
$t\,\Delta U/h=462$ and the velocity difference ![]() $h^2/\Delta U$. Note the difference in scales between (a) and (b).
$h^2/\Delta U$. Note the difference in scales between (a) and (b).
As something of an aside, consider briefly the self-similar behaviour of the surface-averaged mean curvature ![]() $\left \langle \partial n_i/\partial x_i \right \rangle _s\varSigma$. The mean curvature is typically interpreted as the characteristic size of ‘wrinkles’ in the iso-surface. The appropriate scaling of this wrinkling length is somewhat controversial; previous studies have suggested that it scales with an integral scale of the flow (van Kalmthout & Veynante Reference van Kalmthout and Veynante1998), while others imply that it scales with the smallest features in the flow, i.e. the Kolmogorov scale
$\left \langle \partial n_i/\partial x_i \right \rangle _s\varSigma$. The mean curvature is typically interpreted as the characteristic size of ‘wrinkles’ in the iso-surface. The appropriate scaling of this wrinkling length is somewhat controversial; previous studies have suggested that it scales with an integral scale of the flow (van Kalmthout & Veynante Reference van Kalmthout and Veynante1998), while others imply that it scales with the smallest features in the flow, i.e. the Kolmogorov scale ![]() $\eta$ (Kulkarni et al. Reference Kulkarni, Buttay, Kasbaoui, Attili and Bisetti2021). It has also been postulated that the mean curvature is proportional to the peak value of
$\eta$ (Kulkarni et al. Reference Kulkarni, Buttay, Kasbaoui, Attili and Bisetti2021). It has also been postulated that the mean curvature is proportional to the peak value of ![]() $\varSigma$ (Huh, Kwon & Lee Reference Huh, Kwon and Lee2013), although the derivation relies on the ‘generalized’ flame surface density (Boger et al. Reference Boger, Veynante, Boughanem and Trouvé1998) rather than the fine-grained iso-surface area density used here. Despite the differences, results from the current study are consistent with the analysis by Huh et al. (Reference Huh, Kwon and Lee2013), wherein the mean curvature is shown in figures 14(a,b) to evolve at the same rate as the peak value of
$\varSigma$ (Huh, Kwon & Lee Reference Huh, Kwon and Lee2013), although the derivation relies on the ‘generalized’ flame surface density (Boger et al. Reference Boger, Veynante, Boughanem and Trouvé1998) rather than the fine-grained iso-surface area density used here. Despite the differences, results from the current study are consistent with the analysis by Huh et al. (Reference Huh, Kwon and Lee2013), wherein the mean curvature is shown in figures 14(a,b) to evolve at the same rate as the peak value of ![]() $\varSigma$, i.e.
$\varSigma$, i.e. ![]() $\left \langle \partial n_i/\partial x_i \right \rangle _s\sim \varSigma _{max}\sim 1/\lambda _\phi$. It can be seen that the proposed scaling results in a convincing collapse of the instantaneous profiles on the average over the self-similar period, for both of the iso-surfaces shown here.
$\left \langle \partial n_i/\partial x_i \right \rangle _s\sim \varSigma _{max}\sim 1/\lambda _\phi$. It can be seen that the proposed scaling results in a convincing collapse of the instantaneous profiles on the average over the self-similar period, for both of the iso-surfaces shown here.

Figure 14. Proposed self-similar scaling of ![]() $\langle \partial n_i/\partial x_i \rangle _s$ conditioned on (a)
$\langle \partial n_i/\partial x_i \rangle _s$ conditioned on (a) ![]() $\varPhi _{iso}=0.5$ and (b)
$\varPhi _{iso}=0.5$ and (b) ![]() $\varPhi _{iso}=0.95$, and
$\varPhi _{iso}=0.95$, and ![]() $\langle (\partial n_i/\partial x_i)^2 \rangle _s$ conditioned on (c)
$\langle (\partial n_i/\partial x_i)^2 \rangle _s$ conditioned on (c) ![]() $\varPhi _{iso}=0.5$ and (d)
$\varPhi _{iso}=0.5$ and (d) ![]() $\varPhi _{iso}=0.95$. Profiles are plotted as functions of the similarity variable
$\varPhi _{iso}=0.95$. Profiles are plotted as functions of the similarity variable ![]() $\xi =y/h$. Solid and dashed lines are as in figure 6. Note the difference in scales between the various curves.
$\xi =y/h$. Solid and dashed lines are as in figure 6. Note the difference in scales between the various curves.
One might expect that if the mean curvature scales like ![]() $1/\lambda _\phi$, then the mean square curvature would scale with
$1/\lambda _\phi$, then the mean square curvature would scale with ![]() $1/\lambda _\phi ^2$. However, according to the present DNS, the best collapse of the instantaneous profiles of
$1/\lambda _\phi ^2$. However, according to the present DNS, the best collapse of the instantaneous profiles of ![]() $\left \langle (\partial n_i/\partial x_i)^2 \right \rangle _s$ occurs when scaled with
$\left \langle (\partial n_i/\partial x_i)^2 \right \rangle _s$ occurs when scaled with ![]() $1/\eta ^2$. The instantaneous and self-similar profiles are displayed in figures 14(c,d) for
$1/\eta ^2$. The instantaneous and self-similar profiles are displayed in figures 14(c,d) for ![]() $\varPhi _{iso}=0.5$ and
$\varPhi _{iso}=0.5$ and ![]() $\varPhi _{iso}=0.95$, respectively, and demonstrate excellent agreement. From a physical standpoint, this can be understood by considering that the mean curvature is proportional to
$\varPhi _{iso}=0.95$, respectively, and demonstrate excellent agreement. From a physical standpoint, this can be understood by considering that the mean curvature is proportional to ![]() $\left \langle 1/r_1 + 2/r_2 \right \rangle _s$, where
$\left \langle 1/r_1 + 2/r_2 \right \rangle _s$, where ![]() $r_1$ and
$r_1$ and ![]() $r_2$ are the radii of curvature of the iso-surface, and the mean square curvature is proportional to
$r_2$ are the radii of curvature of the iso-surface, and the mean square curvature is proportional to ![]() $\left \langle (1/r_1 + 1/r_2)^2 \right \rangle _s$. Clearly, the effect of the smallest length scales of the surface will dominate the mean square curvature, which is expected to be of the order of the Kolmogorov scale (Sreenivasan, Ramshankar & Meneveau Reference Sreenivasan, Ramshankar and Meneveau1989).
$\left \langle (1/r_1 + 1/r_2)^2 \right \rangle _s$. Clearly, the effect of the smallest length scales of the surface will dominate the mean square curvature, which is expected to be of the order of the Kolmogorov scale (Sreenivasan, Ramshankar & Meneveau Reference Sreenivasan, Ramshankar and Meneveau1989).
These results may be justified further by analogy to canonical scaling arguments involving velocity derivatives. For example, the mean velocity gradient in a shear layer is typically scaled by the mixing layer width ![]() $h$, i.e.
$h$, i.e. ![]() $\left \langle \partial U_i/\partial x_j \right \rangle \sim \Delta U/h$, but the mean of the velocity gradient squared is scaled with the Taylor scale
$\left \langle \partial U_i/\partial x_j \right \rangle \sim \Delta U/h$, but the mean of the velocity gradient squared is scaled with the Taylor scale ![]() $\lambda$, i.e.
$\lambda$, i.e. ![]() $\left \langle (\partial U_i/\partial x_j)^2 \right \rangle \sim \Delta U^2/\lambda ^2$ (Tennekes & Lumley Reference Tennekes and Lumley1972). Therefore, it is not unreasonable to imagine that the mean curvature and mean square curvature scale separately from each other.
$\left \langle (\partial U_i/\partial x_j)^2 \right \rangle \sim \Delta U^2/\lambda ^2$ (Tennekes & Lumley Reference Tennekes and Lumley1972). Therefore, it is not unreasonable to imagine that the mean curvature and mean square curvature scale separately from each other.
Returning now to the destruction term ![]() $\mathcal {D}$, based on the above discussion it is assumed that (1)
$\mathcal {D}$, based on the above discussion it is assumed that (1) ![]() $\mathcal {D}\sim \mathcal {D}_b$, and (2)
$\mathcal {D}\sim \mathcal {D}_b$, and (2) ![]() $\left \langle (\partial n_i/\partial x_i)^2 \right \rangle _s\sim \eta ^{-2}$. This suggests the following self-similar scaling for the destruction,
$\left \langle (\partial n_i/\partial x_i)^2 \right \rangle _s\sim \eta ^{-2}$. This suggests the following self-similar scaling for the destruction,
The instantaneous profiles are shown along with the self-similar average in figure 15, demonstrating the collapse of the profiles over the given self-similar period.

Figure 15. Proposed self-similar scaling of the destruction term ![]() $\mathcal {D}=\left \langle w_{dif}\,\partial n_i/\partial x_i \right \rangle _s\varSigma$ from (3.8), conditioned on (a)
$\mathcal {D}=\left \langle w_{dif}\,\partial n_i/\partial x_i \right \rangle _s\varSigma$ from (3.8), conditioned on (a) ![]() $\varPhi _{iso}=0.5$ and (b)
$\varPhi _{iso}=0.5$ and (b) ![]() $\varPhi _{iso}=0.95$, as functions of the similarity variable
$\varPhi _{iso}=0.95$, as functions of the similarity variable ![]() $\xi =y/h$. Solid and dashed lines are as in figure 6.
$\xi =y/h$. Solid and dashed lines are as in figure 6.
Now, it was demonstrated in figure 5 that the production and destruction terms are significantly larger than the remaining terms in (3.8), but of a similar magnitude to each other, suggesting that the production and destruction should scale similarly. However, from the current discussion, it is proposed that ![]() $\mathcal {D}\sim D/\lambda _\phi \eta ^2$, whereas
$\mathcal {D}\sim D/\lambda _\phi \eta ^2$, whereas ![]() $\mathcal {P}\sim \Delta U/\lambda _\phi ^2$. This discrepancy can be resolved by noting that in the present DNS with constant Schmidt number equal to
$\mathcal {P}\sim \Delta U/\lambda _\phi ^2$. This discrepancy can be resolved by noting that in the present DNS with constant Schmidt number equal to ![]() $0.7$, the Kolmogorov and Batchelor scales are directly proportional, where the Batchelor scale is defined as
$0.7$, the Kolmogorov and Batchelor scales are directly proportional, where the Batchelor scale is defined as ![]() $\eta _B = \eta \,Sc^{-1/2}$. From this definition, and the definition of the Kolmogorov scale in (2.2), it can be shown that
$\eta _B = \eta \,Sc^{-1/2}$. From this definition, and the definition of the Kolmogorov scale in (2.2), it can be shown that
Noting that the Taylor scale, defined in (4.7), is proportional to ![]() $(\varepsilon /\upsilon )^{1/2}$, and that
$(\varepsilon /\upsilon )^{1/2}$, and that ![]() $\lambda _g\sim \lambda _\phi$ in the present DNS, it can be shown that
$\lambda _g\sim \lambda _\phi$ in the present DNS, it can be shown that
Substituting this expression for ![]() $\eta ^2$ into the self-similar form given above for
$\eta ^2$ into the self-similar form given above for ![]() $\mathcal {D}$ yields
$\mathcal {D}$ yields
which is the same as the scaling observed for the production term. Note that although the Schmidt number dependence is included where possible, the present results assume a Schmidt number of ![]() $O(1)$ and may not be valid for flows with Schmidt numbers significantly different from unity, such as hydrogen diffusing in air or diluents such as salt in water. Furthermore, the diffusivity in the present simulations is constant and may not apply for flows with significant temperature or density gradients, such as premixed flames or highly stratified flows.
$O(1)$ and may not be valid for flows with Schmidt numbers significantly different from unity, such as hydrogen diffusing in air or diluents such as salt in water. Furthermore, the diffusivity in the present simulations is constant and may not apply for flows with significant temperature or density gradients, such as premixed flames or highly stratified flows.
6.6. Net effect of production and destruction terms
The final term to analyse is the net effect of production and destruction, ![]() $K=\mathcal {P}-\mathcal {D}$. As discussed briefly in § 5.2, terms
$K=\mathcal {P}-\mathcal {D}$. As discussed briefly in § 5.2, terms ![]() $\mathcal {P}$ and
$\mathcal {P}$ and ![]() $\mathcal {D}$ are both an order of magnitude larger than
$\mathcal {D}$ are both an order of magnitude larger than ![]() $\partial \varSigma /\partial t$ and
$\partial \varSigma /\partial t$ and ![]() $\mathcal {T}_U$. Despite this discrepancy in magnitudes, it is clear that
$\mathcal {T}_U$. Despite this discrepancy in magnitudes, it is clear that ![]() $\partial \varSigma /\partial t$ and
$\partial \varSigma /\partial t$ and ![]() $\mathcal {T}_U$ cannot be neglected. For example, the location of an iso-surface in the present mixing layer, say
$\mathcal {T}_U$ cannot be neglected. For example, the location of an iso-surface in the present mixing layer, say ![]() $\varPhi _{iso}>0.5$, must translate in the
$\varPhi _{iso}>0.5$, must translate in the ![]() $+y$ direction for the mixing layer width to increase with time. Thus a non-trivial value of
$+y$ direction for the mixing layer width to increase with time. Thus a non-trivial value of ![]() $\partial \varSigma /\partial t$ is required. As displayed in figure 5(b), computing the net effect of the production and destruction,
$\partial \varSigma /\partial t$ is required. As displayed in figure 5(b), computing the net effect of the production and destruction, ![]() $K$, yields a term that is of the same order of magnitude as
$K$, yields a term that is of the same order of magnitude as ![]() $\partial \varSigma /\partial t$ and
$\partial \varSigma /\partial t$ and ![]() $\mathcal {T}_U$.
$\mathcal {T}_U$.
Assuming that ![]() $K$ will develop proportionally to
$K$ will develop proportionally to ![]() $\partial \varSigma /\partial t$ and
$\partial \varSigma /\partial t$ and ![]() $\mathcal {T}_U$ yields the self-similar form
$\mathcal {T}_U$ yields the self-similar form
The normalized cross-stream profiles are displayed in figure 16, which once again demonstrates agreement between the instantaneous and time-averaged profiles, aside from some fluctuations around ![]() $y/h=0$. Importantly, the fluctuations observed here are non-monotonic in time, i.e. the error is likely statistical in nature, not systematic. Notably, the scaling proposed here does not agree with the scaling proposed by Kulkarni & Bisetti (Reference Kulkarni and Bisetti2021), who suggest that
$y/h=0$. Importantly, the fluctuations observed here are non-monotonic in time, i.e. the error is likely statistical in nature, not systematic. Notably, the scaling proposed here does not agree with the scaling proposed by Kulkarni & Bisetti (Reference Kulkarni and Bisetti2021), who suggest that ![]() $\mathcal {K}$ would scale in the same manner as
$\mathcal {K}$ would scale in the same manner as ![]() $\mathcal {P}$ and
$\mathcal {P}$ and ![]() $\mathcal {D}$.
$\mathcal {D}$.
7. Discussion
7.1. Summary and Reynolds number scaling
According to the above analysis, the terms responsible for the evolution of ![]() $\varSigma$, given in (3.8), evolve in a self-similar manner according to
$\varSigma$, given in (3.8), evolve in a self-similar manner according to
 \begin{equation} \left. \begin{gathered} \frac{\partial \varSigma}{\partial t} = \frac{\Delta U}{h\lambda_\phi}\,\widehat{\frac{{\rm d}\varSigma}{{\rm d}t}}, \quad \mathcal{T}_t = \frac{\Delta U}{h\lambda_\phi}\,\hat{\mathcal{T}}_t , \quad \mathcal{P} = \frac{\Delta U}{\lambda_\phi^2}\,\hat{\mathcal{P}},\\ \mathcal{T}_D = \frac{D}{h\lambda_\phi^2}\,\hat{\mathcal{T}}_D \quad \mbox{and} \quad \mathcal{D} = \frac{\Delta U}{\lambda_\phi^2}\,\hat{\mathcal{D}}, \end{gathered} \right\} \end{equation}
\begin{equation} \left. \begin{gathered} \frac{\partial \varSigma}{\partial t} = \frac{\Delta U}{h\lambda_\phi}\,\widehat{\frac{{\rm d}\varSigma}{{\rm d}t}}, \quad \mathcal{T}_t = \frac{\Delta U}{h\lambda_\phi}\,\hat{\mathcal{T}}_t , \quad \mathcal{P} = \frac{\Delta U}{\lambda_\phi^2}\,\hat{\mathcal{P}},\\ \mathcal{T}_D = \frac{D}{h\lambda_\phi^2}\,\hat{\mathcal{T}}_D \quad \mbox{and} \quad \mathcal{D} = \frac{\Delta U}{\lambda_\phi^2}\,\hat{\mathcal{D}}, \end{gathered} \right\} \end{equation}
where the length scales ![]() $h$,
$h$, ![]() $\lambda _\phi$ and
$\lambda _\phi$ and ![]() $\eta$ are understood to be functions of time
$\eta$ are understood to be functions of time ![]() $t$. Furthermore, the net effect of production and destruction, i.e.
$t$. Furthermore, the net effect of production and destruction, i.e. ![]() $K=\mathcal {P}-\mathcal {D}$, is found to evolve according to
$K=\mathcal {P}-\mathcal {D}$, is found to evolve according to
Substituting these self-similar forms into (3.8) and multiplying by ![]() $h\lambda _\phi /\Delta U$ yields
$h\lambda _\phi /\Delta U$ yields
 \begin{equation} \widehat{\frac{\partial \varSigma}{\partial t}} = \hat{\mathcal{T}}_t + \frac{h}{\lambda_\phi}\,\hat{\mathcal{P}} + \frac{D}{\lambda_\phi\,\Delta U}\,\hat{\mathcal{T}}_D - \frac{h}{\lambda_\phi}\,\hat{\mathcal{D}}. \end{equation}
\begin{equation} \widehat{\frac{\partial \varSigma}{\partial t}} = \hat{\mathcal{T}}_t + \frac{h}{\lambda_\phi}\,\hat{\mathcal{P}} + \frac{D}{\lambda_\phi\,\Delta U}\,\hat{\mathcal{T}}_D - \frac{h}{\lambda_\phi}\,\hat{\mathcal{D}}. \end{equation}
Note that this equation is not formally self-similar, as the length scales ![]() $h$ and
$h$ and ![]() $\lambda _\phi$ are functions of time, which will be addressed in the next subsection. Despite this, there are some implications regarding the evolution of iso-surface area density than can be extrapolated from this result. First, note that the production and destruction terms are multiplied by the ratio of the mixing layer width to the Taylor length scale. By taking the mixing layer width to be the integral scale of the flow and invoking well-known scaling arguments (Tennekes & Lumley Reference Tennekes and Lumley1972; Pope Reference Pope2000), this ratio is expected to scale like
$\lambda _\phi$ are functions of time, which will be addressed in the next subsection. Despite this, there are some implications regarding the evolution of iso-surface area density than can be extrapolated from this result. First, note that the production and destruction terms are multiplied by the ratio of the mixing layer width to the Taylor length scale. By taking the mixing layer width to be the integral scale of the flow and invoking well-known scaling arguments (Tennekes & Lumley Reference Tennekes and Lumley1972; Pope Reference Pope2000), this ratio is expected to scale like ![]() $h/\lambda _\phi \sim ({Re}\, Sc)^{1/2}$. Based on the proposed Reynolds scaling, it is expected that these terms will become large compared to
$h/\lambda _\phi \sim ({Re}\, Sc)^{1/2}$. Based on the proposed Reynolds scaling, it is expected that these terms will become large compared to ![]() $\partial \varSigma /\partial t$ and
$\partial \varSigma /\partial t$ and ![]() $\mathcal {T}_t$ for highly turbulent flows, i.e.
$\mathcal {T}_t$ for highly turbulent flows, i.e. ![]() ${Re}\,Sc \gg 1$. This is supported by the discrepancy in magnitudes between terms in the present study, e.g. as shown in figure 5(a). Second, the coefficient of the diffusion term
${Re}\,Sc \gg 1$. This is supported by the discrepancy in magnitudes between terms in the present study, e.g. as shown in figure 5(a). Second, the coefficient of the diffusion term ![]() $\mathcal {T}_D$ can also be interpreted according to the Reynolds and Schmidt numbers. By invoking scaling arguments similar to those above, it is suggested that
$\mathcal {T}_D$ can also be interpreted according to the Reynolds and Schmidt numbers. By invoking scaling arguments similar to those above, it is suggested that ![]() $D/(\lambda _\phi \,\Delta U)\sim ({Re}\,Sc)^{-1/2}$ (Tennekes & Lumley Reference Tennekes and Lumley1972; Pope Reference Pope2000). In contrast to the production and destruction terms, the coefficient of the diffusion term is expected to become small compared to
$D/(\lambda _\phi \,\Delta U)\sim ({Re}\,Sc)^{-1/2}$ (Tennekes & Lumley Reference Tennekes and Lumley1972; Pope Reference Pope2000). In contrast to the production and destruction terms, the coefficient of the diffusion term is expected to become small compared to ![]() $\partial \varSigma /\partial t$ for
$\partial \varSigma /\partial t$ for ![]() ${Re}\,Sc\gg 1$, which is supported by the magnitudes of the terms as displayed in e.g. figure 5(b).
${Re}\,Sc\gg 1$, which is supported by the magnitudes of the terms as displayed in e.g. figure 5(b).
Throughout the present analysis, it was found that the centreline values of the turbulent length scales, i.e. ![]() $\lambda _g$,
$\lambda _g$, ![]() $\lambda _\phi$ and
$\lambda _\phi$ and ![]() $\eta$, were general enough to cover the wide range of iso-levels presented herein, from
$\eta$, were general enough to cover the wide range of iso-levels presented herein, from ![]() $\varPhi _{iso}=0.5$ to
$\varPhi _{iso}=0.5$ to ![]() $\varPhi _{iso}=0.95$ (and, by symmetry, to
$\varPhi _{iso}=0.95$ (and, by symmetry, to ![]() $\varPhi _{iso}=0.05$ as well). However, with regard to the Reynolds scaling, there are some distinct differences that can be observed between iso-values between e.g. figures 5(a,c). For the iso-value
$\varPhi _{iso}=0.05$ as well). However, with regard to the Reynolds scaling, there are some distinct differences that can be observed between iso-values between e.g. figures 5(a,c). For the iso-value ![]() $\varPhi _{iso}=0.5$, the production and destruction terms are a full order of magnitude larger than the other terms, whereas the difference (while still significant) is much smaller for the iso-value
$\varPhi _{iso}=0.5$, the production and destruction terms are a full order of magnitude larger than the other terms, whereas the difference (while still significant) is much smaller for the iso-value ![]() $\varPhi _{iso}=0.95$. It is thought that the local value of the Reynolds number is lower towards the outside of the mixing layer, which means that the Reynolds scaling discussed above is not as pronounced for the
$\varPhi _{iso}=0.95$. It is thought that the local value of the Reynolds number is lower towards the outside of the mixing layer, which means that the Reynolds scaling discussed above is not as pronounced for the ![]() $\varPhi _{iso}=0.95$ iso-surface. This might imply that even for very large Reynolds numbers based on the centreline values, iso-surfaces defined near the edge of the mixing, e.g. the turbulent/non-turbulent interface, may exhibit behaviour different to that of iso-surfaces near the centreline of the flow.
$\varPhi _{iso}=0.95$ iso-surface. This might imply that even for very large Reynolds numbers based on the centreline values, iso-surfaces defined near the edge of the mixing, e.g. the turbulent/non-turbulent interface, may exhibit behaviour different to that of iso-surfaces near the centreline of the flow.
It should be noted that the Reynolds and Schmidt number scalings proposed here are inferred from the self-similar behaviour of the present study, which spans a small range of Taylor Reynolds numbers. Additional studies are required (similar to those performed by Shete & de Bruyn Kops Reference Shete and de Bruyn Kops2020; Kulkarni & Bisetti Reference Kulkarni and Bisetti2021) to have more confidence in the Reynolds number dependence of iso-surface area density in a temporal mixing layer.
7.2. Physical interpretation of the surface area density transport equation
A formally self-similar expression for ![]() $\partial \varSigma /\partial t$ in the present study can be obtained by combining the production and destruction terms into their net effect and neglecting the molecular diffusion term, which yields
$\partial \varSigma /\partial t$ in the present study can be obtained by combining the production and destruction terms into their net effect and neglecting the molecular diffusion term, which yields
According to (7.4), the rate of change of ![]() $\varSigma$ at any location in the flow is due to the net growth or decay of the surface due to the combined effects of production and destruction, and the transport of
$\varSigma$ at any location in the flow is due to the net growth or decay of the surface due to the combined effects of production and destruction, and the transport of ![]() $\varSigma$ due to turbulent diffusion. Self-similar profiles of this simplified balance equation for
$\varSigma$ due to turbulent diffusion. Self-similar profiles of this simplified balance equation for ![]() $\varSigma$ are plotted in figure 17.
$\varSigma$ are plotted in figure 17.

Figure 17. Self-similar profiles of the terms in (7.4) for (a) ![]() $\varPhi _{iso}=0.5$ and (b)
$\varPhi _{iso}=0.5$ and (b) ![]() $\varPhi _{iso}=0.95$. Blue circles indicate
$\varPhi _{iso}=0.95$. Blue circles indicate ![]() $\partial \hat {\varSigma }/\partial \hat {t}$, orange squares indicate
$\partial \hat {\varSigma }/\partial \hat {t}$, orange squares indicate ![]() $\mathcal {\hat {T}}_t$, and turquoise diamonds indicate
$\mathcal {\hat {T}}_t$, and turquoise diamonds indicate ![]() $\hat {K}$. Terms have been normalized by
$\hat {K}$. Terms have been normalized by ![]() $h\lambda _\phi /\Delta U$ and averaged over the self-similar period.
$h\lambda _\phi /\Delta U$ and averaged over the self-similar period.
From figure 17(a), it can be seen that for the iso-value ![]() $\varPhi _{iso}=0.5$, there is a net positive effect of
$\varPhi _{iso}=0.5$, there is a net positive effect of ![]() $\mathcal {P}-\mathcal {D}$ near the centre of the mixing layer, but this falls steeply and becomes a net decrease in
$\mathcal {P}-\mathcal {D}$ near the centre of the mixing layer, but this falls steeply and becomes a net decrease in ![]() $\varSigma$ towards the outer edges. This is offset by the turbulent flux term
$\varSigma$ towards the outer edges. This is offset by the turbulent flux term ![]() $\mathcal {T}_t$, which acts in a diffusive manner by decreasing the concentration of
$\mathcal {T}_t$, which acts in a diffusive manner by decreasing the concentration of ![]() $\varSigma$ at the centreline and redistributing it to the outer edge of the mixing layer. The end result is that
$\varSigma$ at the centreline and redistributing it to the outer edge of the mixing layer. The end result is that ![]() $\varSigma$ is shown to decrease in magnitude near
$\varSigma$ is shown to decrease in magnitude near ![]() $y/h=0$, but increase away from the centre, with a local peak near
$y/h=0$, but increase away from the centre, with a local peak near ![]() $y/h\approx \pm 0.4$. This rate of change is consistent with the observed temporal evolution of
$y/h\approx \pm 0.4$. This rate of change is consistent with the observed temporal evolution of ![]() $\varSigma$, which tends to diffuse outwards, as discussed briefly in § 4 and in more detail by Blakeley et al. (Reference Blakeley, Olson and Riley2022).
$\varSigma$, which tends to diffuse outwards, as discussed briefly in § 4 and in more detail by Blakeley et al. (Reference Blakeley, Olson and Riley2022).
For the iso-value ![]() $\varPhi _{iso}=0.95$, the self-similar profiles are displayed in figure 17(b). Here, the net effect of
$\varPhi _{iso}=0.95$, the self-similar profiles are displayed in figure 17(b). Here, the net effect of ![]() $\mathcal {P}-\mathcal {D}$ is positive towards the far outside of the mixing layer, with a maximum occurring near
$\mathcal {P}-\mathcal {D}$ is positive towards the far outside of the mixing layer, with a maximum occurring near ![]() $y/h\approx 0.65$, which decreases and becomes a net destruction of
$y/h\approx 0.65$, which decreases and becomes a net destruction of ![]() $\varSigma$ closer to the centreline, with a minimum occurring near
$\varSigma$ closer to the centreline, with a minimum occurring near ![]() $y/h\approx 0.2$. This is rather counterintuitive, as
$y/h\approx 0.2$. This is rather counterintuitive, as ![]() $\varepsilon$ and
$\varepsilon$ and ![]() $\chi$ are greatest around
$\chi$ are greatest around ![]() $y/h=0$ (as shown in figures 2c,d), which are expected to increase
$y/h=0$ (as shown in figures 2c,d), which are expected to increase ![]() $\varSigma$. The turbulent flux is found to promote iso-surface movement of
$\varSigma$. The turbulent flux is found to promote iso-surface movement of ![]() $\varSigma$ towards the centre of the mixing layer, rather than towards the edges as might be expected for a diffusive term. This could be due to the fact that the turbulent fluctuations are concentrated near
$\varSigma$ towards the centre of the mixing layer, rather than towards the edges as might be expected for a diffusive term. This could be due to the fact that the turbulent fluctuations are concentrated near ![]() $y/h=0$ (as shown in figure 2a), causing the iso-surface to skew in that direction. Overall, the behaviour of
$y/h=0$ (as shown in figure 2a), causing the iso-surface to skew in that direction. Overall, the behaviour of ![]() $\partial \varSigma /\partial t$ is consistent with the results discussed in § 4, which is to translate
$\partial \varSigma /\partial t$ is consistent with the results discussed in § 4, which is to translate ![]() $\varSigma$ in the
$\varSigma$ in the ![]() $+y$ direction. It is interesting to note that the translation in the
$+y$ direction. It is interesting to note that the translation in the ![]() $+y$ direction is actually driven by the production and destruction terms, and is impeded by the turbulent flux. This is opposite to the behaviour observed for
$+y$ direction is actually driven by the production and destruction terms, and is impeded by the turbulent flux. This is opposite to the behaviour observed for ![]() $\varPhi _{iso}=0.5$, in which
$\varPhi _{iso}=0.5$, in which ![]() $\varSigma$ was produced in the region of greatest turbulent fluctuations and diffused outwards. It is unclear why the behavior appears to change as a function of
$\varSigma$ was produced in the region of greatest turbulent fluctuations and diffused outwards. It is unclear why the behavior appears to change as a function of ![]() $\varPhi _{iso}$; additional investigation into the kinematics may prove enlightening.
$\varPhi _{iso}$; additional investigation into the kinematics may prove enlightening.
8. Conclusions and future work
This study is a continuation of the work described by Blakeley et al. (Reference Blakeley, Olson and Riley2022), which examined the self-similar evolution of iso-surface area density ![]() $\varSigma$ of a passive scalar field in a turbulent, temporal mixing layer for a wide range of iso-values. In the present work, the transport equation for
$\varSigma$ of a passive scalar field in a turbulent, temporal mixing layer for a wide range of iso-values. In the present work, the transport equation for ![]() $\varSigma$ is considered in detail for the same turbulent flow and same iso-values of the passive scalar field. It was first demonstrated that the terms in the iso-surface area and the iso-surface area density transport equations could be computed fairly accurately, such that the left-hand and right-hand sides of the transport equation were in approximate balance. Next, the self-similar behaviour of each of the five terms in the iso-surface area density equation (3.8) was examined in detail, and self-similar forms were proposed for each term based upon scaling arguments and the behaviour of the data. Based on these self-similar forms, a scaling analysis of (3.8) suggests that, separately, terms
$\varSigma$ is considered in detail for the same turbulent flow and same iso-values of the passive scalar field. It was first demonstrated that the terms in the iso-surface area and the iso-surface area density transport equations could be computed fairly accurately, such that the left-hand and right-hand sides of the transport equation were in approximate balance. Next, the self-similar behaviour of each of the five terms in the iso-surface area density equation (3.8) was examined in detail, and self-similar forms were proposed for each term based upon scaling arguments and the behaviour of the data. Based on these self-similar forms, a scaling analysis of (3.8) suggests that, separately, terms ![]() $\mathcal {P}$ and
$\mathcal {P}$ and ![]() $\mathcal {D}$, relating to the production and destruction of iso-surface area density, are significantly larger in magnitude than
$\mathcal {D}$, relating to the production and destruction of iso-surface area density, are significantly larger in magnitude than ![]() $\partial \varSigma /\partial t$. However, the net effect of the production and destruction,
$\partial \varSigma /\partial t$. However, the net effect of the production and destruction, ![]() $K=\mathcal {P}-\mathcal {D}$, is of the same order of magnitude as
$K=\mathcal {P}-\mathcal {D}$, is of the same order of magnitude as ![]() $\partial \varSigma /\partial t$. Finally, the results are summarized in figure 17, which displays the self-similar transport of
$\partial \varSigma /\partial t$. Finally, the results are summarized in figure 17, which displays the self-similar transport of ![]() $\varSigma$ based on the proposed scaling identified above. The physical interpretation of the remaining terms, namely the turbulent flux and net effect of production and destruction, is straightforward, although the result for
$\varSigma$ based on the proposed scaling identified above. The physical interpretation of the remaining terms, namely the turbulent flux and net effect of production and destruction, is straightforward, although the result for ![]() $\varPhi _{iso}=0.95$ is somewhat counter-intuitive.
$\varPhi _{iso}=0.95$ is somewhat counter-intuitive.
The present work is focused on gaining a deeper fundamental understanding of iso-surface production, destruction and transport in turbulent flows in order to serve as a baseline comparison to future studies. As such, the problem set-up considered here is one of the most ‘simple’ free shear flow with a passive scalar field. Future work will examine more complicated flow geometries, such as the temporally developing jet. Although it may appear to be a simple extension of the present work, there are subtle differences that require additional understanding. In particular, consider a jet with scalar concentration ![]() $\varPhi =1$ issuing into a quiescent environment with
$\varPhi =1$ issuing into a quiescent environment with ![]() $\varPhi =0$. As the jet mixes into the surrounding fluid, the centreline concentration will decrease, such that the iso-surface area associated with values of
$\varPhi =0$. As the jet mixes into the surrounding fluid, the centreline concentration will decrease, such that the iso-surface area associated with values of ![]() $\varPhi _{iso}$ near
$\varPhi _{iso}$ near ![]() $\varPhi =1$ will go to zero. In this case, it is unclear how
$\varPhi =1$ will go to zero. In this case, it is unclear how ![]() $\partial \varSigma /\partial t$ and the relevant terms will scale; preliminary results suggests that the magnitude of
$\partial \varSigma /\partial t$ and the relevant terms will scale; preliminary results suggests that the magnitude of ![]() $\partial \varSigma /\partial t$ could become comparable to the production and destruction terms (Blakeley et al. Reference Blakeley, Wang and Riley2019), despite
$\partial \varSigma /\partial t$ could become comparable to the production and destruction terms (Blakeley et al. Reference Blakeley, Wang and Riley2019), despite ![]() ${Re}\,Sc\gg 1$. This has significant implications for modelling reacting flows, as the length of a diffusion flame will depend on a proper estimation of when the stoichiometric iso-surface area goes to zero.
${Re}\,Sc\gg 1$. This has significant implications for modelling reacting flows, as the length of a diffusion flame will depend on a proper estimation of when the stoichiometric iso-surface area goes to zero.
Furthermore, the methodology utilized here for estimating iso-surface integrals is expected to be valuable for investigating other turbulent mixing problems that can be described as iso-surfaces, such as premixed flames and the turbulent/non-turbulent interface. These two problems are of particular interest, because the propagation speed of the iso-surface depends on other factors (i.e. reaction rate in a premixed flame and vortex stretching in the turbulent/non-turbulent interface) in addition to the propagation due to molecular diffusivity. These additional effects may have a significant impact on terms ![]() $\mathcal {T}_D$ and
$\mathcal {T}_D$ and ![]() $\mathcal {D}$ in (3.8), which would in turn affect the self-similar behaviour discussed above.
$\mathcal {D}$ in (3.8), which would in turn affect the self-similar behaviour discussed above.
Acknowledgements
B.C.B. would like to thank B. Cabot for his mentorship and assistance with the Miranda code, and wishes him a happy retirement. Direct numerical simulations were performed with the help of B. Cabot and A. Cook on the Lassen supercomputer at Lawrence Livermore National Laboratory. Lawrence Livermore National Laboratory is operated by Lawrence Livermore National Security, LLC, for the US Department of Energy, National Nuclear Security Administration under contract DE-AC52-07NA27344.
Funding
B.C.B. is grateful to the Defense Science and Technology Fellowship from LLNL and the Mechanical Engineering Department at the University of Washington for funding this research. J.J.R. was funded by the Office of Naval Research via grant N00014-19-1-2154.
Declaration of interests
The authors report no conflict of interest.
Appendix. Iso-value dependence on transport terms
In the interests of clarity, only the iso-values ![]() $\varPhi _{iso}=0.5$ and
$\varPhi _{iso}=0.5$ and ![]() $0.95$ were discussed in the main text. These values were chosen because they represent two distinct regions of the flow:
$0.95$ were discussed in the main text. These values were chosen because they represent two distinct regions of the flow: ![]() $\varPhi _{iso}=0.5$ is located primarily towards the centreline of the flow where the turbulent fluctuations are the largest, whereas
$\varPhi _{iso}=0.5$ is located primarily towards the centreline of the flow where the turbulent fluctuations are the largest, whereas ![]() $\varPhi _{iso}=0.95$ is located primarily near the edge of the mixing layer in a region characterized by considerable intermittency. By demonstrating self-similarity for iso-surfaces interacting with these two distinct regions of the flow, it can be stated that iso-surfaces corresponding to intermediate values of
$\varPhi _{iso}=0.95$ is located primarily near the edge of the mixing layer in a region characterized by considerable intermittency. By demonstrating self-similarity for iso-surfaces interacting with these two distinct regions of the flow, it can be stated that iso-surfaces corresponding to intermediate values of ![]() $\varPhi _{iso}$ demonstrate similar behaviours. In figure 18, each term in the transport equation for
$\varPhi _{iso}$ demonstrate similar behaviours. In figure 18, each term in the transport equation for ![]() $\varSigma$ is plotted for the iso-values
$\varSigma$ is plotted for the iso-values ![]() $\varPhi _{iso}=0.5,0.65,0.75,0.85,0.95$ in order to visualize their dependency on
$\varPhi _{iso}=0.5,0.65,0.75,0.85,0.95$ in order to visualize their dependency on ![]() $\varPhi _{iso}$. Note that no values of
$\varPhi _{iso}$. Note that no values of ![]() $\varPhi _{iso} < 0.5$ are shown here, which will be mirrored about
$\varPhi _{iso} < 0.5$ are shown here, which will be mirrored about ![]() $y/h=0$ due to problem symmetry.
$y/h=0$ due to problem symmetry.

Figure 18. Self-similar profiles of each iso-surface transport term described in (3.8) and (5.4): (a) rate- of-change of iso-surface area density, (b) advection, (c) production, (d) normal diffusion, (e) destruction and (f) net effect of production and destruction. The curves in each plot are shown for the iso-values ![]() $\varPhi _{iso}=0.5,0.65,0.75,0.85,0.95$, with the peaks of the curves trending left to right in that order.
$\varPhi _{iso}=0.5,0.65,0.75,0.85,0.95$, with the peaks of the curves trending left to right in that order.