Published online by Cambridge University Press: 17 October 2012
The instability of high-temperature jets is studied because of its importance to the analysis of gas-turbine engine exhaust flow, shock–shock interaction and bypass transition. The focus is on fluid–chemistry coupling, where the chemical time scales are supported by both reactive and inelastic molecular processes. The former are associated with dissociation/exchange reactions, while the latter are associated with transfers of vibrational quanta. The interaction affects both the instability growth rate and acoustic feedback by sustaining thermo-acoustic damping. Resonance conditions are identified as those that yield the maximum damping against the Damköhler number. The main results of the present study are the explanation of the dichotomy between vortical and acoustic modes in relation to the thermo-acoustic damping, and the analysis of the resonance condition as it depends on the physico-chemical properties of carbon/oxygen mixtures. The ability of a mode to support thermo-acoustic damping is related to the local convective Mach number of its most amplified frequency, and thus to the phenomenon of acoustic trapping in the jet core. Regarding the second issue, carbon dioxide acts as the best damper at low jet temperatures  ${T}_{j} \approx 1000~\mathrm{K} $, where the vibrational relaxation is the main chemical scale, and up to
${T}_{j} \approx 1000~\mathrm{K} $, where the vibrational relaxation is the main chemical scale, and up to 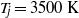 ${T}_{j} = 3500~\mathrm{K} $ because its reactive chemistry resonates with the fluid fluctuation at a lower temperature than the dissociation of
${T}_{j} = 3500~\mathrm{K} $ because its reactive chemistry resonates with the fluid fluctuation at a lower temperature than the dissociation of 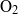 ${\mathrm{O} }_{2} $. At higher temperatures, oxygen is the best damper because of the larger endothermicity of the reactions it supports.
${\mathrm{O} }_{2} $. At higher temperatures, oxygen is the best damper because of the larger endothermicity of the reactions it supports.