Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T22:18:50.227Z Has data issue: false hasContentIssue false
  • English
  • Français

On steady non-breaking downstream waves and the wave resistance

Published online by Cambridge University Press:  08 July 2015

Dmitri V. Maklakov  and
Alexander G. Petrov
Dmitri V. Maklakov*
Affiliation:
N.I. Lobachevsky Institute of Mathematics and Mechanics, Kazan (Volga region) Federal University, Kremlyovskaya 35, Kazan 420008, Russia
Alexander G. Petrov
Affiliation:
Institute for Problems in Mechanics of the Russian Academy of Sciences, prosp. Vernadskogo 101, block 1, Moscow 119526, Russia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work we have obtained exact analytical formulae expressing the wave resistance of a two-dimensional body by the parameters of the downstream non-breaking waves. The body moves horizontally at a constant speed $c$ in a channel of finite depth 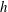$h$. We have analysed the relationships between the parameters of the upstream flow and the downstream waves. Making use of some results by Keady & Norbury (J. Fluid Mech., vol. 70, 1975, pp. 663–671) and Benjamin (J. Fluid Mech., vol. 295, 1995, pp. 337–356), we have rigorously proved that realistic steady free-surface flows with a positive wave resistance exist only if the upstream flow is subcritical, i.e. the Froude number 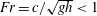$\mathit{Fr}=c/\sqrt{gh}<1$. For all solutions with downstream waves obtained by a perturbation of a supercritical upstream uniform flow the wave resistance is negative. Applying a numerical technique, we have calculated accurate values of the wave resistance depending on the wavelength, amplitude and mean depth.

JFM classification

Waves/Free-surface Flows: Channel flow Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 776 , 10 August 2015 , pp. 290 - 315
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benjamin, T. B. 1995 Verification of the Benjamin–Lighthill conjecture about steady water waves. J. Fluid Mech. 295, 337–356.Google Scholar
Benjamin, T. B. & Lighthill, M. J. 1954 On cnoidal waves and bores. Proc. R. Soc. Lond. A 224, 448–460.Google Scholar
Binder, B. J., Vanden-Broek, J.-M. & Dias, F. 2009 On satisfying the radiation condition in free-surface flows. J. Fluid Mech. 624, 179–189.Google Scholar
Binnie, A. M. 1952 The flow of water under a sluice-gate. Q. J. Mech. Appl. Maths 5, 395–407.Google Scholar
Cokelet, E. D. 1977 Steep gravity waves in water of arbitrary uniform depth. Proc. R. Soc. Lond. A 286, 183–230.Google Scholar
Dias, F. & Vanden-Broek, J.-M. 1989 Open channel flows with submerged obstructions. J. Fluid Mech. 206, 155–170.CrossRefGoogle Scholar
Dias, F. & Vanden-Broek, J.-M. 2002 Generalised critical free-surface flows. J. Engng Maths 42, 291–301.Google Scholar
Dias, F. & Vanden-Broek, J.-M. 2004 Trapped waves between submerged obstacles. J. Fluid Mech. 509, 93–102.Google Scholar
Duncan, J. H. 1983 A note on the evaluation of the wave resistance of two-dimensional bodies from measurements of the downstream wave profile. J. Ship Res. 27 (2), 90–92.Google Scholar
Forbes, L. K. 1982 Non-linear, drag-free flow over a submerged semi-elliptical body. J. Engng Maths 16, 171–180.Google Scholar
Forbes, L. K. 1988 Critical free-surface flow over a semi-circular obstruction. J. Engng Maths 22, 3–13.CrossRefGoogle Scholar
Forbes, L. K. & Schwartz, L. W. 1982 Free-surface flow over a semicircular obstruction. J. Fluid Mech. 114, 299–314.Google Scholar
Holmes, R. J., Hocking, G. C., Forbes, L. K. & Baillard, N. Y. 2013 Waveless subcritical flow past symmetric bottom topography. Eur. J. Appl. Maths 24, 213–230.CrossRefGoogle Scholar
Keady, G. & Norbury, J. 1975 Waves and conjugate streams. J. Fluid Mech. 70, 663–671.Google Scholar
Lord Kelvin 1887 On ship waves. Proc. Inst. Mech. Engrs 38, 409–434.Google Scholar
Lamb, H. 1932 Hydrodynamics, 6th edn. Cambridge University Press.Google Scholar
Levi-Civita, T. 1925 Détermination rigoureuse des ondes permanentes d’ampleur finie. Math. Ann. 93, 264–314.Google Scholar
Longuet-Higgins, M. S. 1975 Integral properties of periodic gravity waves of finite amplitude. Proc. R. Soc. Lond. A 342, 157–174.Google Scholar
Longuet-Higgins, M. S. & Fox, M. J. H. 1977 Theory of the almost-highest wave: the inner solution. J. Fluid Mech. 80, 721–741.Google Scholar
Longuet-Higgins, M. S. & Fox, M. J. H. 1978 Theory of the almost-highest wave. Part 2. Matching and analytical extension. J. Fluid Mech. 85, 769–786.Google Scholar
Longuet-Higgins, M. S. & Fox, M. J. H. 1996 Asymptotic theory for the almost-highest solitary wave. J. Fluid Mech. 317, 1–19.CrossRefGoogle Scholar
Maklakov, D. V. 1995 Flow over an obstruction with generation of nonlinear waves on the free surface: liniting regimes. Fluid Dyn. 30 (2), 245–253.Google Scholar
Maklakov, D. V. 1997 Nonlinear Problems of Hydrodynamics of Potential Flows with Unknown Boundaries. Yanus-K (in Russian).Google Scholar
Maklakov, D. V. 2002 Almost highest gravity waves on water of finite depth. Eur. J. Appl. Maths 13, 67–93.Google Scholar
Miles, J. W. 1986 Stationary, transcritical channel flow. J. Fluid Mech. 162, 489–499.Google Scholar
Naghdi, P. M. & Vongsarnpigoon, L. 1986 The downstream flow beyond an obstacle. J. Fluid Mech. 162, 223–236.Google Scholar
Nalimov, V. I. 1982 Stationary surface waves over an uneven bottom. Dinamika Splosn. Sredy 58, 108–156 (in Russian).Google Scholar
Salvesen, N. & von Kerczek, C. 1976 Comparison of numerical and perturbation solutions of two-dimensional nonlinear water–wave problems. J. Ship Res. 20 (3), 160–170.Google Scholar
Schwartz, L. W. 1974 Computer extension and analytic continuation of stokes expansion for gravity waves. J. Fluid Mech. 62, 553–578.Google Scholar
Shen, S. S. P. & Shen, M. C. 1990 On the limit of subcritical free-surface flow over an obstacle. Acta Mechanica 82, 225–230.Google Scholar
Sivakumaran, N. S., Tingsanchali, T. & Hosking, R. J. 1983 Steady shallow flow over curved beds. J. Fluid Mech. 128, 469–487.Google Scholar
Tanaka, M. 1986 The stability of solitary waves. Phys. Fluids 29 (3), 650–655.Google Scholar
Vanden-Broek, J.-M. 1987 Free-surface flow over an obstruction in a channel. Phys. Fluids 30 (8), 2315–2317.Google Scholar
Wehausen, J. V. & Laitone, E. V. 1960 Surface waves. In Handbuch der Physics (ed. Truesdell, C.), vol. 9. Springer.Google Scholar
Whitham, G. B. 1962 Mass, momentum and energy flux in water waves. J. Fluid Mech. 12, 135–147.Google Scholar
Williams, J. M. 1981 Limiting gravity waves in water of finite depth. Phil. Trans. R. Soc. Lond. A 302, 139–180.Google Scholar